基于非線性算法的制造資源多目標優化配置模型研究

楊培義 張天彤 張慧勤

摘 要：為優化配置多目標制造資源，分析了制造資源生產能力的約束和資源供應狀態的約束;用非線性動態規劃算法，按照經濟效益最先性原則，構建了一套制造資源多目標優化配置模型;以G試驗器材制造公司為例，結合自編的MATLAB算法求解，然后提出計算機輔助算法，運用EXCEL進行檢驗;實證表明，在生產要素約束條件下，實現了多目標資源優化配置，完成了生產定制，滿足了顧客需求;驗證了構建的非線性多目標資源優化配置模型可行性和自編程序的正確性，并且該模型難度適中、易于操作。由此表明，該模型可為多目標制造資源優化提供實踐指導和理論依據。

關鍵詞：非線性算法;動態規劃法;制造資源;資源優化;MATLAB算法

0 引言

多目標企業制造資源主要包括人力、廠房、設備、工藝技術、軟件、物料、信息、服務、財務等資源，簡稱物質流、信息流、資金流，有廣義概念和狹義概念之分，廣義概念是指原材料進廠到成品出廠整個生產周期的物質流、價值流、信息流所涉及的生產要素，也包括研發設計、生產制造、銷售交付等相關過程涉及的要素。狹義概念是指加工制造、生產裝配一個零部件所需要的物質元素，主要包括工裝等。多目標制造資源優化配置Manufacturing Resources Optimal Allocation （MROA），是通過一定的調度方式把有限的人財物等生產要素資源合理分配到企業的各個生產單元中，以實現資源最佳利用，獲取最佳效益。隨著時代經濟的發展，智能產品、復雜產品、高尖端產品不斷面世，新的制造資源優化模型和方法也不斷出現，很多學者針對不同環境、不同目的展開廣泛研究，已從面向單一信息化模式發展到面向不同信息化應用模式，支持產品全生命周期應用[1-2]。如張中偉[3]等人針對如何優化設計工藝和機械加工制造資源提出非線性工藝規劃資源優化配置模型，并運用遺傳算法求解;藍伯雄[4]等人針對傳統MRP邏輯存在固有缺陷，提出一種基于滾動計劃的動態企業資源優化模型。葛家家[5]等人針對服務型企業的特點和特征，提出以資源和時間作為決策變量構建項目資源優化模型，包北方[6]等人為實現產品定制協同生產，提出產品定制協同MROA的雙層規劃求解方案。蔣南云[7]等人為尋求出廠檢驗環節的最優運行策略，應用Jackson排隊網絡理論，研究了出廠檢驗環節檢驗設備、運輸車輛及抽檢人員的資源配置優化問題。付銀環[8]、李奧典[9]等人提出基于兩階段隨機規劃法建模應用于灌區水資源優化配置。本文主要針對制造系統在人財物等生產要素有限資源約束下，引入非線性動態規劃算法，建立一套動態監控機制，以實現人財物等資源優化配置。動態規劃是美國數學家貝爾曼等人提出的解決多目標多階段決策過程優化的一種方法[10]，在工業、服務業、交通運輸、現代物流等領域得到了廣泛應用，并且獲得了顯著的效果[11-15]。

1 制造資源優化模型形成方案

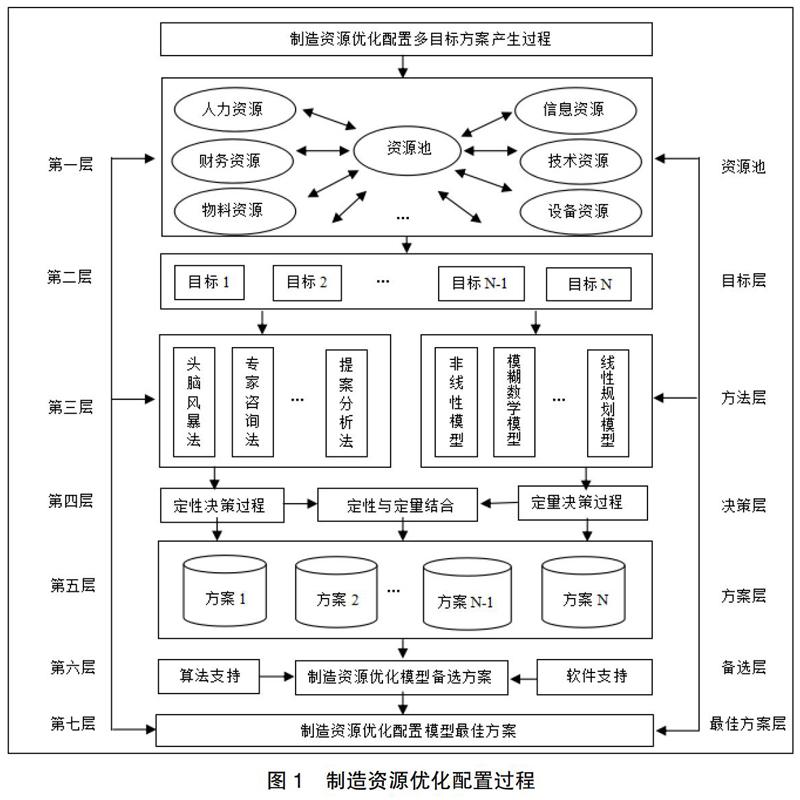
制造資源優化配置（Manufacturing Resources Optimal Allocation，MROA）不僅要考慮生產能力資源約束，還要考慮資源供應狀態的約束。生產能力資源一般指與研發設計、生產制造和交付銷售相關的三大流，即物質流、信息流、資金流。它是支撐現代制造業生產規模和產能的基本要素，與市場需求有密切關系;當市場需求上升時，則需要考慮如何增加制造資源供應，以滿足市場需求的增長;當需求不足時，則需要考慮如何縮小資源規模，避免生產能力過剩，減少三大流損失。資源供應的狀態主要反映產品在制造過程中制造資源使用的狀況，是生產能資源重要的組成部分，此外，生產能資源與其存在線性關系，生產能力資源會隨著資源供應狀態的變化而變化，而資源供應狀態恰好反映其在特定時間內是否可用[16-17]。本文主要針對生產能力在各種資源約束下，引入非線性算法，建立一套動態監控機制，以實現多目標人財物等MROA，如圖1所示，多目標MROA產生的過程，第一層為資源池，是企業在生產過程中需要調配的各種資源，其中人力資源、物料資源、設備資源等組成物質流，和財務相關的資源組成資金流，技術資源、信息資源、軟件資源等組成信息流;第二層為目標層，用于描述優化資源配置的多目標性;第三層與第四層分別為方法層和決策層，是確定最佳目標，采用的方法和策略;第五層為方案層，是經過第四層定性定量決策篩選、評估所形成的多個優化方案;第六層為優化模型備選層，可針對不同備選的優化模型，采用合適的算法和相關軟件，求解模型;第七層為最佳方案層，經過相應算法驗證求解，篩選出最佳資源優化配置模型。本文將生產能力資源視作制造資源的靜態屬性，重點研究資源受限對非線性動態規劃算法設計的生產計劃能力的影響，以G綠色能源公司為例，按照顧客生產定制要求，運用非線性算法構建多目標資源優化配置模型。

2 非線性算法構建優化模型

2.1 基本思想

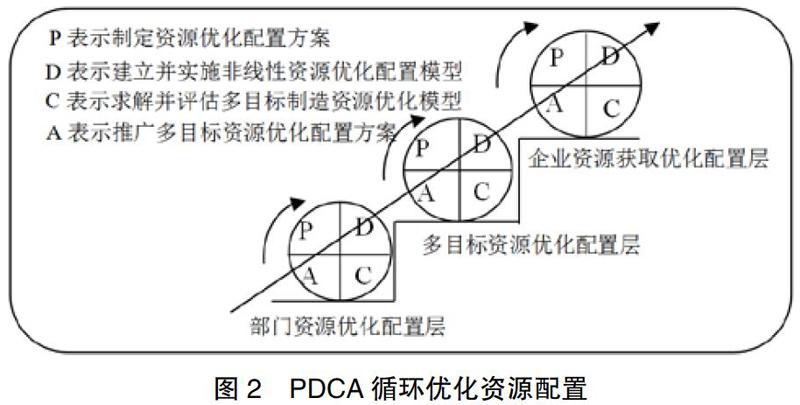
在本文采用的非線性算法是指動態規劃法，動態規劃算法的優勢在于利用最優化原理給出最優值函數的遞推關系式和邊界條件，首先將多目標問題劃分為若干個相互聯系的階段，然后選取狀態變量和決策變量，寫出狀態轉移方程及定義最優值函數。從而把多目標多層次問題轉為若干個同類型的子問題，再逐個求解。PDCA循環優化資源配置如圖2所示，把多目標資源優化配置看成相互聯系的多階段問題，賦予其狀態變量和決策變量，然后運用非線性動態規劃算法建模，按照PDCA循環爬樓梯上升式的資源優化，每轉動一周，即進行一輪優化方法，表示制造資源優化配置一層。

2.2 動態規劃建模

（1）將多目標問題看成一個有機整體，根據需要劃分為若干個子問題階段;

（2）根據實際情況，選取狀態變量;

（3）根據多目標問題給定的前提條件，定義決策變量并確定每個子問題決策集合;

（4）寫出問題狀態轉移方程;

（5）確定各個子問題的階段指標，列出最優策略基本方程并求解。

2.3 動態規劃求解

（1）按照多目標問題的時空特征，把其分為若干個子問題并編號;

（2）確定各個子問題的各種客觀情況，用不同狀態表示并且狀態的選擇要滿足無后效性，狀態變量和狀態集合分別用和表示;

（3）確定決策變量和允許決策集合;

（4）確定階段指標;

（5）確定問題狀態轉移方程;

（6）確定求解邏輯順序，并給出相應的遞推公式或方程，包括邊界條件;

（7）實施迭代求解。

2.4 動態規劃的數學模型

從多目標資源配置問題中，求解并遞推非線性動態規劃基本方程：

其中目標函數;階段指標;稱為邊界條件。

3 案例分析

G為試驗器材制造公司，主要生產冷熱沖擊試驗機，產品規格、功率、型號按照顧客要求來確定，以節約制造資源，保證產品和生態質量為核心，與顧客訂立生產定制合同，在5個月內生產臺數為10的倍數的冷熱沖擊試驗機，假如G公司每月產量上限為100臺冷熱沖擊試驗機，此產品可存儲，庫存費用為每臺200元/月，月需求量及每臺制造成本見表1。現在要求在兩種情況下確定月出產量：1月初無存貨和1月初有20臺庫存;要求既能滿足顧客每月生產定制的合同需求量，又能使冷熱沖擊試驗機生產資源成本和庫存費用達到最小。

3.1 分析問題

本案例是一個典型的非線性規劃多目標生產定制問題，這里可把這個問題的解決動態地視為各個月先后做出決策的過程——多目標的決策過程，在每月做生產決策時，不能單純地考慮本月制造費用，因為本月生產決策會對以后各個月的生產決策產生影響，而應考慮從本月初直到第4月低的生產制造成本費用（總指標），并且每月的生產決策只依賴于各月初存貨量與以前造成的貨存量無關，因此，這是一個5階段多目標動態規劃問題，適合采用逆序法建立多目標制造資源優化模型來解題，第1階段是1月份，…，第5階段是5月份。

3.2 建立多目標制造資源優化模型

定義符號如下：

表示在滿足顧客合同需求量時，使冷熱沖擊試驗機生產資源成本和庫存費用達到最小;

基本方程為：

3.3 求解過程分析

3.3.1 決策變量

表示第個月的冷熱沖擊試驗機生產量，表示第階段開始的冷熱沖擊試驗機存儲量。

3.3.2 約束條件

對于每個月來說，生產量、需求量和月初庫存滿足如下關系：

下月初冷熱沖擊試驗機庫存量=本月初庫存量+本月生產量-本月需求量

即類似狀態轉移方程：，分別如下。

第1個月：初始庫存由給定值a確定;

由題意知，在此表示6月初的存儲量，實際也是5月末的存儲量，根據題意，5月末的庫存量應該為零，這是一個隱含約束條件，是問題約束邊界。生產能力限制：每月生產能力為100，由于產量限制為10的倍數，故可令，為整數且：。

3.3.3 目標函數

本題的目標是總費用最低。而總費用=每月的生產費用+庫存費用，即：

3.3.4 數學建模

最終可得如下數學模型：

3.4 應用MATLAB求解

根據3.3節求解過程分析，編寫如下代碼：

Function u = DecisFun（k，x）

%% 函數功能說明

%產量的決策函數

%% 函數主體部分

q = 10*[6，8，10，9，8]; %每月的實際需求量

if q（k）-x < 0? ? ? ?%每月的實際需求量小于庫存量時，產量為0～100

u = 0：100;

else

u = q（k）-x：100; %每月的實際需求量大于庫存量時，產量為需求量扣除庫存量～100

end

u = u（：）;

Function v =Sub0bjFun（k，x，u）

%% 函數功能說明

%求解階段k的指標函數（成本）

%%函數主體部

c = [70，72，80，72，75];

v = c（k）*u+200*x;

Function w =TransFun（k，x，u）

%% 函數功能說明

%狀態轉移方程

%% 函數主體部分

q = 10*[6，8，10，9，8];

w = x+u-q（k）;

%% 函數功能說明

%利用動態規劃逆序算法（DTGHNX）求解制造資源多目標優化配置問題

%狀態轉移方程

%%函數主體部分

q = 10*[6，8，10，9，8];

w = x+u-q（k）;

%% 文件主體部分

clc，clear %清除命令窗口，清除工作空間

x = nan*ones（14，5）; %x是10的倍數，最大范圍0<=x<=130，共有5個階段，故賦予x初值為14×5的矩陣

%按階段（月）定義x的可能取值，由具體問題確定階段數

x（1：7，1） = 10*（0：6）';? ?%1階段（月）x的可能取值

x（1：11，2） = 10*（0：10）'; %2階段（月）x的可能取值

x（1：13，3） = 10*（0：12）'; %3階段（月）x的可能取值

x（1：14，4） = 10*（0：13）'; %4階段（月）x的可能取值

x（1：9，5） = 10*（0：8）';? ?%5階段（月）x的可能取值

[p，f]=DTGHNX（x， @DecisFun， @SubObjFun， @TransFun）; %由于Obj

Fun（v，f）=v+f， 故輸入ObjFun省略

%輸出結果

fprintf（'（1）各階段（月）的庫存、生產量和成本為：＼n'）

disp（' 序號 庫存 產量 成本'）

disp（p）

fprintf（'（2）總成本的最小值為（萬元：＼n'）， disp（f）

disp（f）

3.5 結果分析

（1）執行結果，各階段輸出結果（截取部分數據），見下表2。

總成本見運行結果統計表3：下表中行1數值表示1月初庫存量為0臺時，5個月總成本為30070萬元;行3數值表示1月初庫存20臺時，5個月總成本28590萬元。

如輸出結果所示，由各階段（月）的庫存，生產量和成本輸出結果的第1個和第3個5行（紅線框內）可以看出1月初無存貨和有存貨20臺的最優生產決策，并由總成本輸出結果的第1行和第3行可以得知，對應5個月的總成本分別為30070萬元和28590萬元。現將其歸納制成表4。

3.6 利用EXCEL驗證MATLAB運行結果

為便于利用計算機輔助軟件Excel驗證求解，需要依據非線性動態規劃問題的特點將關聯數據導入Excel工作表。求解該模型的EXCEL電子表如表5和表6所示。

由表5可知，利用EXCEL求解的結果為1月初的庫存為0時，各月的生產量分別為100臺、100件、40臺、100臺和70臺，總成本最低，值為30070萬元。

如表6所示，當1月初冷熱沖擊試驗機庫存量為20臺時，各月的生產量分別為100臺、100臺、20臺、100臺與70臺，總成本最低，值為28590萬元。

綜上與MATLAB運行結果對比，結果完全一致，驗證了優化配置模型可行性和自編算法的正確性，完成了顧客生產定制計劃，達到了預期目標。

4 結論

本文通過多目標資源優化問題的進行研究可得到如下成果：

（1）分析了多目標資源優化配置模型形成過程，按照經濟效益最先性原則，提出一種非線性動態規劃算法，構建了以資源消耗最少，經濟效益獲取最大目標資源優化配置模型，為解決多目標資源優化問題提供了一種新思路。（2）以根據顧客要求而定制的生產計劃訂單為例，通過實證分析，驗證了生產定制多目標資源優化配置模型可行性和有效性。（3）針對多目標資源優化配置模型求解問題，運用自編的MATLAB算法求解，然后用EXCEL驗證，驗證了該算法的正確性，為類似多目標資源優化配置問題的求解提供了一種新方法。

本文分析了多目標制造資源優化模型形成過程，借鑒了已有的資源優化配置模型，針對制造資源受限對生產計劃定制的影響，利用非線性動態規劃算法，建立一套制造資源優化模型，最后通過案例分析驗證了該方法的有效性，為今后展開多目標多層次制造資源優化奠定了基礎。

參考文獻：

[1]房亞東，杜來紅，何衛平等.網絡化制造環境下多維度制造資源建模技術研究[J].計算機應用研究，2009，26（02）：553-556.

[2]冀阿強，段曉峰.面向云制造的制造資源模型研究[J].中國制造業信息化，2012，41（17）：5-8.

[3]張中偉，唐任仲，陶俐言.基于滾動計劃的動態企業資源優化模型[J].計算機集成制造系統，2016，22（02）：516-528.

[4]藍伯雄，姜楠.基于滾動計劃的動態企業資源優化模型[J].運籌與管理，2010，19（03）：127-143.

[5]葛家家，李賢功，胡婷.服務型制造的項目資源優化模型研究[J].科技管理研究，2015（19）：211-215.

[6]包北方，楊育等.產品定制制造資源優化配置[J].計算機集成制造系統，2014，20（08）：1807-1818.

[7]蔣南云，張琳，張英豪等.基于Jackson排隊網絡的出廠檢驗環節資源配置優化[J].工業工程與管理，2016，12（01）：45-53.

[8]付銀環，郭萍等.基于兩階段隨機規劃方法的灌區水資源優化配置[J].農業工程學報，2014，45（05）73-81.

[9]李奧典，唐德善等.基于圖論的麗水市多水源供水配置模型研究[J].華東交通大學學報，2016，33（01）：107-113.

[10]胡運權，郭耀煌.運籌學教程[M].北京：清華大學出版社，1998.

[11]饒建偉，胡偉文.基層部隊人力資源優化配置的動態規劃模型研究[J].運籌與管理，2009，18（05）：43-48.

[12]遲國泰，余方平等.基于動態規劃多期期貨套期保值優化模型研究[J].中國管理科學，2010，18（03）：17-24.

[13]呂志民，宋肖青，董紹華.鋼鐵聯合企業中期生產計劃建模及算法[J].計算機集成制造系統，2011，17（01）：89-94.

[14]鄒淵，侯仕杰，韓爾樑，劉林，陳銳.基于動態規劃的混合動力商用車能量管理策略優化[J].汽車工程，2012，34（08）：663-668.

[15]曾強，沈玲，吳立云，蘭建義.一種改進的綜合生產計劃動態規劃優化方法[J].計算機工程與應用，2014，50（21）：248-253.

[16]王佩，田錫天等.基于車間能力的工藝分工規劃方法研究[J].機械科學與技術，2011，30（05）：833-843.

[17]陽陽，莫蓉等.MBD模式下制造資源信息機加工藝應用研究[J].制造業自動化，2012，34（07）：21-25.

基金項目：國賽項目融入實訓教學促進城軌交通車輛專業教學改革的研究與實踐（2017SJGLX568）

作者簡介：楊培義（1991-），男，河南睢縣人，碩士研究生，助教，主要研究方向：計算機應用、自動化檢測。

為通訊作者