初談《三角形內角和定理》輔助線作用

趙凌

摘 要：三角形內角和定理的證明，可通過添加輔助線構造新圖形形成新關系，如何建立已知和未知的橋梁，問題轉化進行證明。

關鍵詞：三角形內角;定理;平行線

在小學階段同學們會信心十足地說：“我用量角器量過許多三角形的內角，每一個三角形三個內角的和確實都等于180°”，或者說：“我們曾把許多三角形紙片的三個角剪下來，拼成一個平角，得到三角形的內角和是1800”。或者通過折一折的幾何操作方法來確認“三角形的內角和是1800”，但是對于“三角形內角和1800 ”的形成過程卻不知道？我們動手操作的實踐過程中會不會出現誤差？不管是度量還是拼角都會存在誤差;那么我們能不能用其他方法證明這個命題？

到了初中階段通過嚴格的幾何證明得出了“三角形的內角和等于180°”，在課本中是直接利用平行線的性質通過平移角的方法來證明的.對初中生來說添加輔助線是很難的，因為這是他們第一次通過添加輔助線來證明題目.為了不讓初中生對添加輔助線產生畏懼，教師一定要引導、設計好這一課，但是我們該如何給學生講清楚為什么要添加輔助線，讓學生“知其然，知其所以然”，讓學生在基于認知和生產的數學思維基礎上的開花、結果。這就要求教師要運用自己的智慧和魅力不斷地培養學生的創新能力和發散思維能力，鼓勵學生大膽實驗，小心求證。這既能擺脫習慣思維的束縛，拓寬思維范圍，又能使創造性思維能力得到發展，以適應當前素質教育的需要。

介紹新法、激發興趣

一、操作實驗法

法國數學家帕斯卡11歲時，在玩長方形時發現：長方形沿對角線折疊得到兩個完全相同的直角三角形。他想：任意長方形的四個直角之和是3600，那么兩個完全一樣的直角三角形的內角和就是1800，所以他進一步推斷“任意三角形的內角和為1800”。

二、推理證明法

方法一

分析：因為? ∠B=∠2

所以MA∥BC

因為? ∠C=∠3

所以NA∥BC

因為 過直線外一點有且只有一條直線與已知直線平行，所以M、N、A在同一條直線上，所以∠MAN=1800

從而得到：

要想證明三角之和等于180度，那么我們要借助平行線，所以在這里添加輔助線。

證明：過A點作MN∥BC

因為MN∥BC

所以∠B=∠2 ，∠C=∠3

因為∠MAN=180°? ，∠A+∠2+∠3=180°

所以

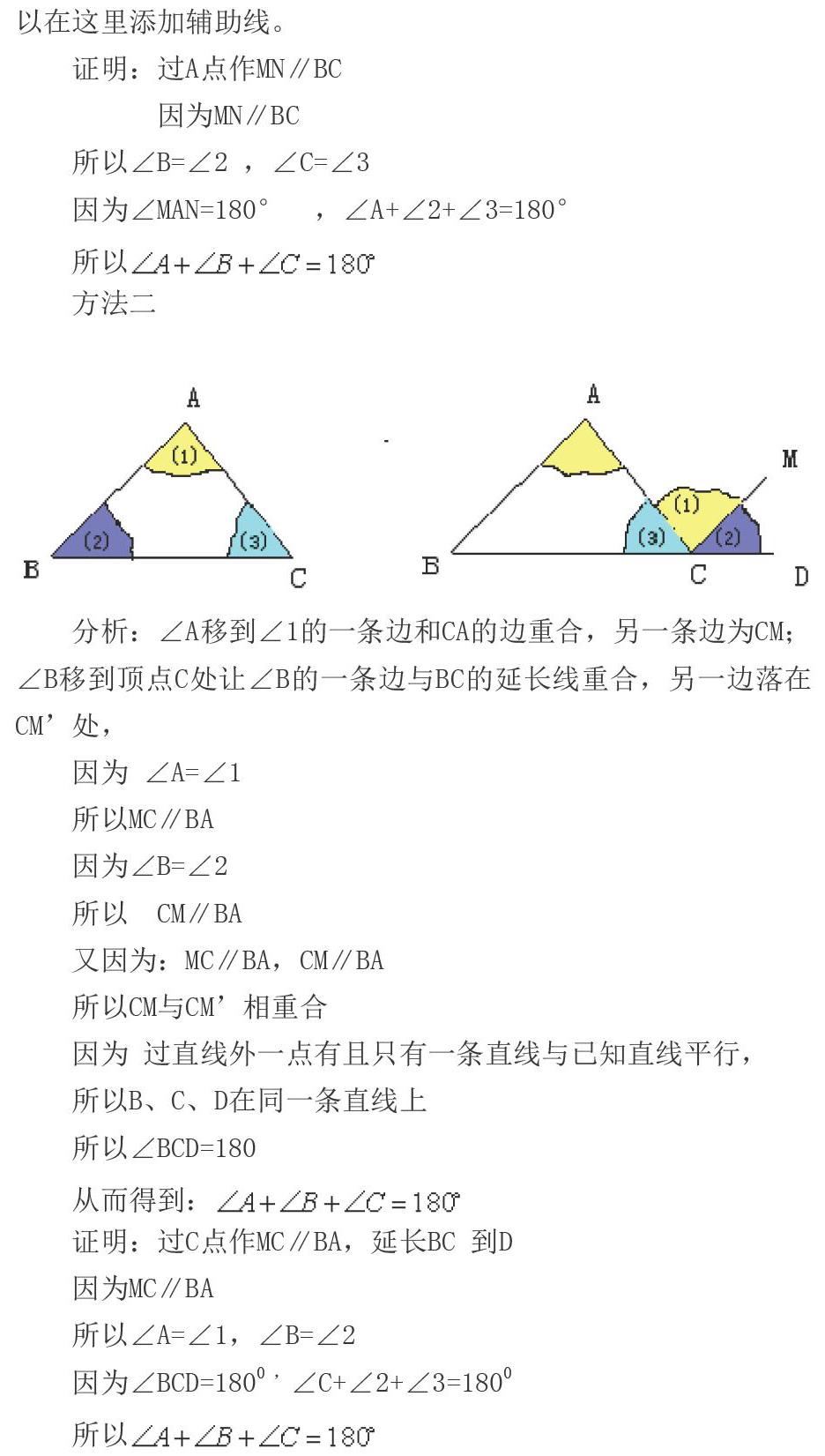
方法二

分析：∠A移到∠1的一條邊和CA的邊重合，另一條邊為CM;∠B移到頂點C處讓∠B的一條邊與BC的延長線重合，另一邊落在CM處，

因為 ∠A=∠1

所以MC∥BA

因為∠B=∠2

所以? CM∥BA

又因為：MC∥BA，CM∥BA

所以CM與CM相重合

因為 過直線外一點有且只有一條直線與已知直線平行，

所以B、C、D在同一條直線上

所以∠BCD=180

從而得到：

證明：過C點作MC∥BA，延長BC 到D

因為MC∥BA

所以∠A=∠1，∠B=∠2

因為∠BCD=1800 ，∠C+∠2+∠3=1800

所以

波利亞在《怎樣解題》中說道“聰明的學生和讀者不會滿足于只驗證推理的各個步驟都是正確的，他們也想知道各個步驟的動機和目的，如果一條巧妙的輔助線和輔助圖形突然出現在圖形中看不出什么動機，并且令人驚訝的解決出了問題，那么聰明的學生會和讀者會感到很失望，她們覺得上當受騙了。”通過以上兩種推理證明方法，深刻的向學生講清楚幾何證明過程中的“為什么”。

參考文獻

[1]《中學數學教師需要具備怎么的知識》 新疆師范大學 楊軍