基于圖像紋理特征的礦井水災感知方法
孫繼平,曹玉超
(中國礦業大學(北京) 機電與信息工程學院,北京 100083)
水災是煤礦重特大事故之一[1-3]。盡早發現水災,撤出井下作業人員,及時排水和堵水,救出遇險人員,是減少事故傷亡和財產損失的有效措施[4-7]。水災監測方法主要有水位監測法、微震監測法和水文鉆孔法。文獻[8]設計了一套電容式液位傳感器系統,通過電容式液位傳感器采集礦井水位信號進行處理,計算出水位和水位上升速率,超出閾值發出報警信號,但不能發現礦井水災。微震監測法通過監測煤炭開采過程中壓力改變[9]造成的煤巖破壞,以及形成的導水通道產生的微震信號監測水災發生,文獻[10]利用微震信號突變分析底板斷層突水,但容易受到沖擊地壓、煤與瓦斯突出等影響。文獻[11]通過采集處理施工井下放水孔、水文觀測孔及地面鉆孔水流量、水位信息,研究了水位-流量耦合規律,頂板滲透性、覆巖變形規律及其與含水層水位變化關系、裂采比與垮采比對頂板水害影響。這些方法在水災防治工作中發揮著重要作用,但存在著適應性差、誤報和漏報率高等問題,難以滿足煤礦安全生產需求。因此,有必要研究礦井水災感知方法。
1 基于圖像紋理特征的礦井水災感知方法
1.1 工作原理
在常溫常壓下,水是無色、無味、透明液體。但礦井突水時,在巷道和采掘工作面快速流動的水會產生波紋。水波紋理同周圍煤、巖石、設備等相比,有明顯的區別。根據礦井突水時,快速流動的水在巷道和采掘工作面產生波紋的特征,筆者提出了基于圖像紋理特征的水災感知方法。
基于圖像紋理特征的水災感知方法工作原理如下:在巷道頂部或巷幫、采煤工作面支架等設置攝像機,實時采集采掘工作面和巷道底板圖像;通過雙樹復小波變換,提取水、煤、巖石圖像紋理特征,構造泊松分布過程,估計強度特征參數;通過相似性測度,對水、煤、巖石圖像進行分類,建立水災圖像識別模型;根據水災圖像識別模型,對實時監測的圖像進行識別,當分割圖像具有水災紋理特征時,進行水災報警。
圖像紋理在雙樹復小波域中具有良好的可區分性。水、煤、巖石的圖像紋理具有顯著的差異。隨著分解層級加深,圖像紋理特點的抽象特征會得以展現。單純的分層系數特征對于圖像紋理描述較為單薄,為提高識別率,筆者研究了雙樹復小波塔式分解第n+1層在第n層條件下系數的概率分布,提出了基于圖像紋理特征的礦井水災感知方法,工作原理如圖1所示。訓練樣本圖像分別經過1,2級分解,圖像的紋理特征信息可以由系數反映,煤、巖石紋理[12-15]和水的紋理有明顯區別:系數的方差可以展現較深的紋理,例如煤、巖石或水表面的起伏,水滴之間的邊緣等,方差越大,表示這些起伏越多;系數的期望可以表現紋理的致密程度,期望值越大,表示樣本的紋理越緊致。層級不同對紋理的刻畫表示不同:一級統計系數可以展現距離比較近的紋理特征;二級統計系數可以發現高層抽象的紋理特征,而二級雙樹復小波是在一級基礎上展開的,所以與一級有密切關系。為此筆者構造了泊松分布模型來描述1,2級雙樹復小波系數統計值之間的關系,并計算其泊松分布模型的強度參數作為學習庫,待測樣本進行同樣的操作和學習到的特征進行相似性比較歸類。
基于圖像紋理特征的水災感知算法如圖2所示。圖像在某一方向經過雙樹復小波一級變換后,統計其系數的方差和期望;在進行二級變換后,繼續統計其系數方差和期望,構造泊松分布過程模型并進行參數估計,得到強度系數。其他方向進行相同的操作,得到6個方向的強度系數組成方差強度系數向量和期望強度系數向量。學習其特征,并以此特征作為待測樣本判斷依據。
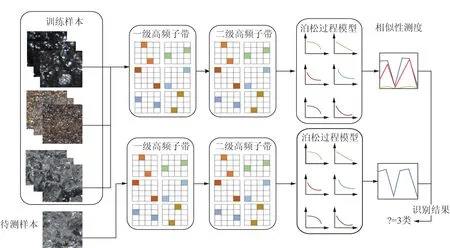
圖1 基于圖像紋理特征的水災感知方法工作原理Fig.1 Working principle of flood perception method based on image texture features

圖2 基于圖像紋理特征的水災感知算法框架Fig.2 Flood disaster perception algorithm framework based on image texture features
1.2 雙樹復小波變換與泊松分布
傳統的DWT(離散小波變換)具有多分辨分析,時頻局部化,快速算法等諸多優點。但是在處理圖像紋理時,存在震蕩、混疊、平移改變、有限的方向選擇性。這些局限性限制了DWT在圖像特征提取方面的應用,輸入信號發生較大的平移會改變小波系數的分布,其根源在于其二元下抽樣,而且只能對水平、垂直、對角線3個方向的特征進行分析。Kingsburry受傅里葉變換的啟發提出了雙樹復小波變換(Dual-tree Complex WaveletTransform,DT-CWT)[16]的概念,二維DT-CWT保持了傳統DWT的良好的時頻局部化的分析能力,而且具有近似的平移不變性、方向選擇性、數據冗余等優點。雙樹復小波原理為
ψc(t)=ψh(t)+jψg(t)
(1)
其中,f(t)∈L2(R),
(2)
相應的有
dc(j,n)=dh(j,n)+jdg(j,n)
(3)
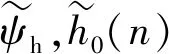
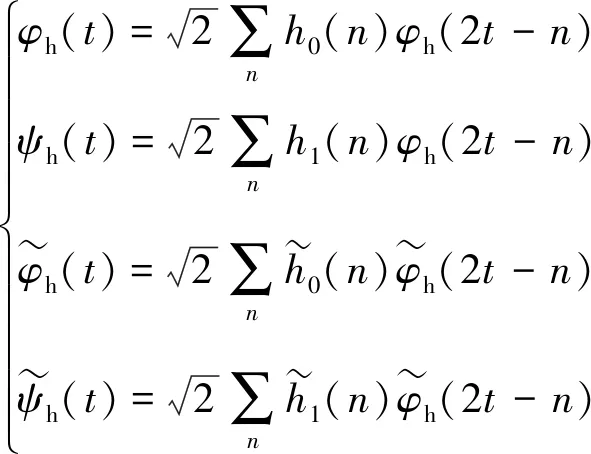
(4)
相應的對于虛部有

(5)
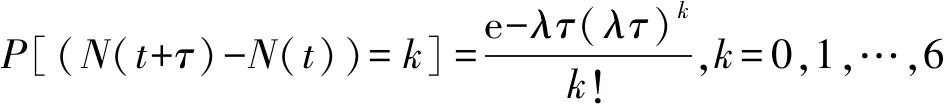
類似的二維雙樹復小波可定義如下
ψc(x,y)=ψ(x)ψ(y)=(ψh(x)+jψg(x))×
(ψh(y)+jψg(y))=ψh(x)ψh(y)-ψg(x)ψg(y)+
j(ψg(x)ψh(y)+ψh(x)ψg(y))
(6)
可得
j(φg(x)ψh(y)+φh(x)ψg(y))]
j(ψg(x)φh(y)+ψh(x)φg(y))]
j(ψg(x)ψh(y)+ψh(x)ψg(y))]
j(φg(x)ψh(y)-φh(x)ψg(y))]
j(ψg(x)φh(y)-ψh(x)φg(y))]
j(ψg(x)ψh(y)-ψh(x)ψg(y))]
(7)
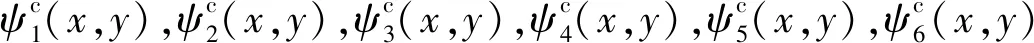
離散隨機過程{X(t),t∈T}的狀態空間為E,如果對任意的t1 F(x,|xn,xn-1,…,x2,xn,tn,tn-1,…, t2,t1)=F(x|xn,tn) (8) 所以有 P{X(t)=x|X(tn)=xn,…,X(t1)= x1}=P{X(t)=x|X(tn)=xn} (9) 則泊松分布為 (k=0,1,…,6) (10) 其中,±15°為±45°時刻隨機變量;±75°為延時±75°時刻;±75°為強度參數;-15°為正整數,記同一子帶中方差的樣本集為 X={k1,k2,…,kN} (11) 根據最大似然估計,令α=λτ, (12) (13) 分別求lf(k;α)對α的導數為0,即 (14) 分析上式可得 (15) 定義X,Y兩個向量的皮爾遜相關系數如下: (17) (18) 按照公式計算兩個向量的相關系數,并以此作為判據計算2個圖像的相似度。 為了驗證本文提出的基于圖像紋理特征的水災感知方法的可行性和有效性,筆者采用c++編程,在Intel i5、四核1.8 GHz、內存8 G、64位操作系統,visual studio 2013上進行了實驗。實驗由750幅圖像組成,其中煤樣本圖像250幅,巖石圖像250幅,波動的水圖像250幅,圖像尺寸為256×256。隨機從每類樣本中選取20%(50幅)圖像作為訓練樣本,其他80%(200幅)圖像作為測試樣本。為了補償和平衡相似性測度,統計學習樣本的強度系數λ,并將強度系數的最小值作為補償值,平移學習樣本和待測樣本的強度系數λ。 不同方向的方差強度系數如圖3所示。隨機在3類樣本中抽取50個樣本,計算每個樣本中的σ2的強度系數λ,6幅圖分別為-15°,-75°,-45°,15°,75°,45°六個方向的λ幅值圖。可以看出在±15°,±45°,±75°六個方向上巖石圖像與煤和水波圖像的紋理有明顯的區別,說明這4個方向巖石有明顯的紋理。而在這6幅圖像中煤樣本圖像強度系數在每個方向的幅值都很小,有波紋的水的圖像的強度系數次之,巖石圖像的方差強度系數λ的均值最大,整體高于其他2種圖像,表示有波紋的水的紋理比煤的圖像的紋理更加緊致,比巖石的圖像紋理寬松。在±75°方向有波紋的水的圖像強度系數λ的均值和煤、巖石圖像強度系數λ的均值差值較為明顯,并且振幅較大,說明在±75°高頻方向的系數特征表示有波紋的水的紋理較其他2種圖像區分能力最大。水中波紋是有一定方向的,或是弧形的波紋,或是帶狀的,或是幾個波形的疊加,是有一定的規律的,并不是雜亂無章的;礦井突水過程中,突水源可能是一個,也可能是多個,波形的成型受到突水源、傳播過程中的障礙物、巷道壁反射等,會形成具有一定的方向的波形,所以會呈現出如圖3(c),(e)所示的情況。 不同方向的期望強度系數如圖4所示。隨機在3類樣本中抽取50個樣本,計算每個樣本的期望E的強度系數λ。6幅圖分別為-15°,-75°,-45°,15°,75°,45°六個方向的λ幅值圖。巖石在±15°,±45°四個方向上的λ幅值在以0為中心震動,說明巖石圖像在此方向下紋理變化較弱,波動特征說明了巖石圖像中某些雜質或是噪聲的干擾產生了類似紋理的效果。±75°方向中有波紋的水和巖石圖像的期望E強度系數λ震蕩幅值高于煤圖像的λ值,說明有波紋的水和巖石的紋理比煤的紋理不均勻且變化較大。圖4(b)中,煤圖像值振幅要比有波紋的水的振幅小,說明在這個方向后者的紋理比煤的紋理更加清晰。振幅則有力的刻畫了煤紋理的不均勻程度要低于此方向后者的圖像,可見強度系數λ不僅能作為圖像紋理清晰程度之間的量化關系,幅值高說明圖像紋理明顯,更能清晰的刻畫圖像紋理的均勻程度,震蕩的幅值越大說明圖像紋理越不均勻。 不同方向的方差和期望強度系數如圖5所示。圖5(a)為-15°,-75°,-45°,15°,75°,45°方向高頻子帶系數方差的泊松分布的強度系數λ;圖5(b)為-15°,-75°,-45°,15°,75°,45°方向高頻子帶系數期望的泊松分布的強度系數λ。可以看到煤圖像在每個方向的幅值基本都比較小,說明波動的水和巖石的圖像在各個方向的紋理都比煤圖像更加清晰,圖5所示描述比較符合客觀事實。在-15°,-75°,15°,75°方向上,有波紋的水的圖像幅值都大于或等于煤的圖像,是因為前者圖像的紋理在每個方向顯示都更為清晰,尤其是在-75°和75°方向上,兩幅圖像具有更好的可區分性。同時可以看出圖像在-15°,-75°,-45°,15°,75°,45°方向上的強度系數λ是基本對稱的,是因為煤與有波紋的水的圖像基本為線性的,所以當圖像旋轉180°后的特征和旋轉之前基本相似。圖5(b)中,在-75°和75°方向,λ值能有力區分煤,巖石和有波紋水的圖像,同時可見在-15°等方向也是基本對稱的。 圖3 不同方向的方差強度系數Fig.3 Variance intensity coefficients in different directions 圖4 不同方向的期望強度系數Fig.4 Expected strength coefficient in different directions 圖5 不同方向的方差和期望強度系數Fig.5 Variance and expected strength coefficient in different directions 表1所示為3個樣本的期望E和方差σ2的泊松分布的強度系數λ。首先計算待測樣本的λ值,并將各個方向的參數λ值組成向量,然后分別計算待測樣本與3個樣本的皮爾遜相關系數分別為0.881 153,0.790 790,0.970 694。根據本文第3節相似性測度,可以判斷出待測樣本為有波紋的水。 不同算法正確識別率見表2。參與比較實驗的其他方法包括期望方差相似性測度(EX-DX-P1)、期望方差補償相似性測度(EX-DX-P2)。濾波器為多貝西(Daubechies)小波函數構造的6抽頭的濾波器組[18-19],分別為{ 0.002 6,-0.052 0,0.166 4,0.557 8,0.394 7,-0.020 6,-0.063 6,0.014 8},{0.014 8,0.063 6,-0.020 6,-0.394 7,0.557 8,-0.166 4,-0.052 0,-0.002 6},{0.014 8,-0.063 6,-0.020 6,0.394 7,0.557 8,0.166 4,-0.052 0,0.002 6},{-0.002 6,-0.052 0,-0.166 4,0.557 8,-0.394 7,-0.020 6,0.063 6,0.014 8},分別計算樣本在{±15°,±45°,±75°}6個方向的期望和方差,計算待測樣本與3個樣本之間的皮爾遜相關系數PCC(Pearson Correlation Coefficient)值。其中EX-DX-P2為將系數進行平衡補償后的效果,可以看到在本組實驗中,準確率略有提高3個百分點,但是整體效果還是有些勉強。本文算法采用的濾波器設置與EX-DX-P1和EX-DX-P2相同,在兩級變換后并將兩級相應的值按照本文第二節構造泊松分布模型,計算其強度參數λ值,構成向量,計算待測向量與樣本向量的PCC值,本文算法的平均識別率達81%。表2的實驗結果表明:筆者所提出的在雙樹復小波變換中應用泊松分布過程提取參數的假設是合理的,本文算法能夠很好的區分待測樣本圖像。 表1 樣本分類特征 參數煤樣本巖樣本有波紋水待測樣本方差(方向2)35.185 612107.714 89040.983 19228.809 629方差(方向3)44.714 474114.522 53071.609 94781.143 349方差(方向4)7.577 95222.176 3138.551 1625.028 345方差(方向6)36.495 209111.943 71046.289 16235.657 246方差(方向7)46.603 584121.412 59879.082 73398.812 828方差(方向8)7.379 10022.731 8298.896 1615.809 229期望(方向2)66.877 46470.600 80066.198 50265.416 328期望(方向3)49.700 37122.999 90821.630 8679.105 694期望(方向4)68.094 48268.333 44367.092 94967.565 933期望(方向6)65.455 20060.773 19065.076 97365.169 281期望(方向7)82.474 762107.727 798108.702 454121.179 283期望(方向8)68.098 55768.236 77867.078 2067.583 977皮爾遜相關系數0.881 1530.790 7900.970 694 表2 不同識別算法的正確識別率 Table 2 Correct recognition rates of different recognition algorithms % 由表3可以看出,EX-DX-P1與EX-DX-P2耗時相當,分別為153 ms和152 ms,本文算法耗時171 ms左右,這是因為本文算法需要對泊松模型進行建模估計其強度系數λ會帶來時間的消耗,這個是系數組成泊松分布過程的缺點,也是展現高層次紋理特征的優點所在,是以犧牲時間為代價的。但是這些時間性能的開銷換來的是識別率的大幅提升,大概為15%,這些多出時間是可以容忍的。綜上所述,本算法的識別率達81%,高于其他算法,雖然運算時間略長,但完全可以滿足水災感知需求。 表3 不同識別算法的平均耗時 Table 3 Average time-consuming of different recognition algorithmsms (1)提出了基于圖像紋理特征的礦井水災感知方法:在巷道頂部或巷幫、采煤工作面支架等設置攝像機,實時采集采掘工作面和巷道底板圖像;通過雙樹復小波變換,提取水、煤、巖石圖像紋理特征,構造泊松分布過程,估計強度特征參數;通過相似性測度,對水、煤、巖石圖像進行分類,建立水災圖像識別模型;根據水災圖像識別模型,對實時監測的圖像進行識別,當分割圖像具有水災紋理特征時,進行水災報警。 (2)建立了雙樹復小波域泊松分布模型,首先對學習樣本進行雙樹復小波變換,提取1,2級系數,統計其方差與期望值,利用相應的方差與期望值構造泊松分布模型,并估計其各個方向模型強度參數。對待測樣本同樣進行雙樹復小波變換后利用1,2級系數的方差與期望值構成的模型的強度參數向量與樣本參數向量進行皮爾遜相似性比較,最終確定待測樣本分類,并分析了模型的強度系數在圖像紋理的區分能力。 (3)采集了水災模擬實驗圖像,建立了圖像數據庫。對所提出的模型編制了相應的實驗程序,進行了模型的訓練和實驗驗證,研究了水、煤、巖石在雙樹復小波域泊松分布下系數統計值的分布規律,并對模型的性能進行了參數化的評估,本文算法在時間開銷增加14 ms情況下,準確率提升約15%。 (4)礦井水災圖像經過雙復小波變換后,在各層級相應系數統計值之間的關系符合泊松分布的假設,并通過大量的實驗證明了該假設的合理性。 (5)實驗驗證了基于圖像紋理特征的礦井水災感知方法的可行性。實驗表明,基于圖像紋理特征的礦井水災感知方法,識別水災準確率大于81%。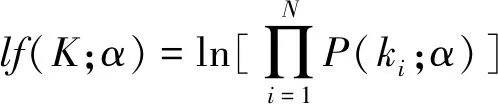
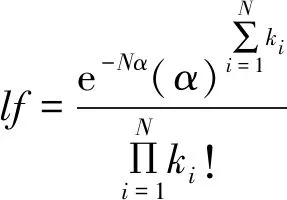

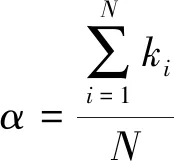
1.3 相似性測度
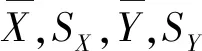
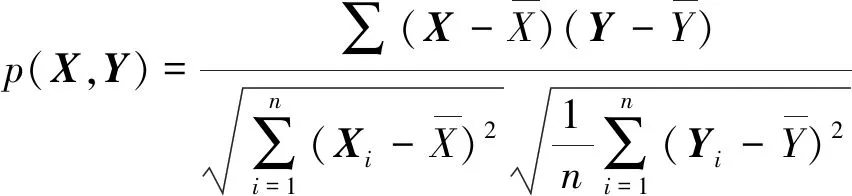
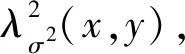
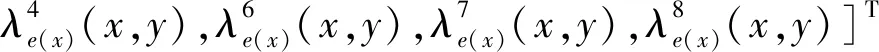
2 實驗研究
2.1 實驗設置
2.2 不同樣本的分類特征
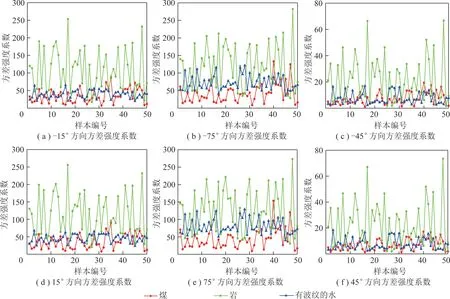
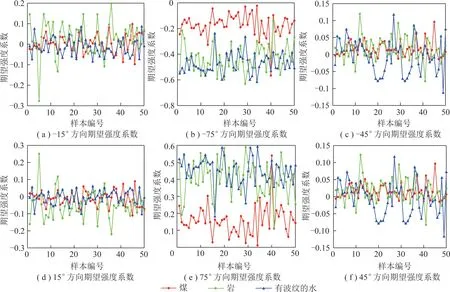
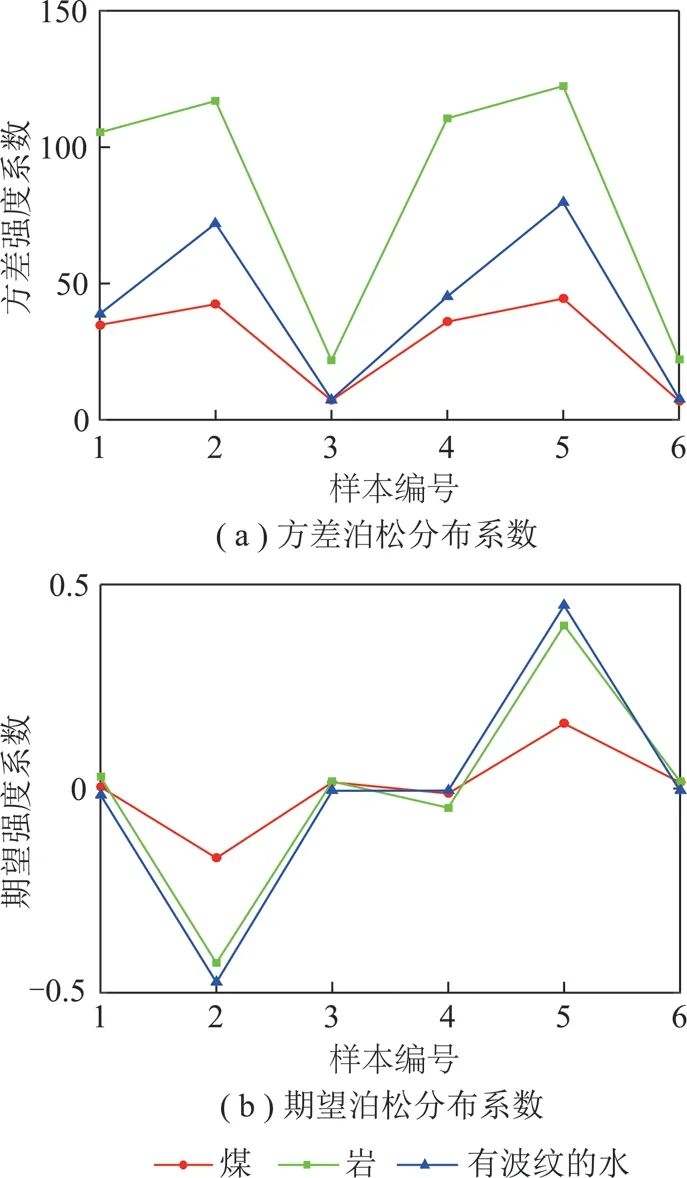
2.3 樣本分類
3 試驗分析
3.1 不同算法正確識別率的比較
Table 1 Sample classification characteristics

3.2 不同算法平均耗時的比較
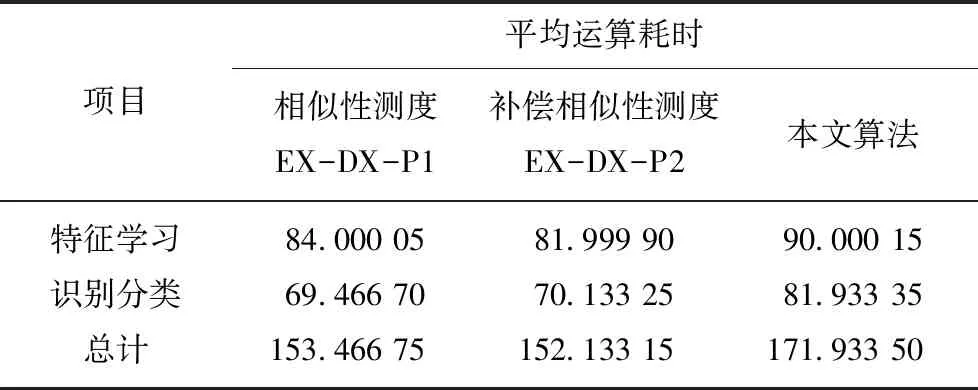
4 結 論

