含弧形預制裂隙砂巖力學特征試驗研究

朱 棟，靖洪文，尹 乾，陶祥令，宗義江

(1.中國礦業大學 力學與土木工程學院，江蘇 徐州 221116; 2.江蘇建筑職業技術學院 能源與交通工程學院，江蘇 徐州 221116)

在地質調查和巖體工程建設中經常會遇到大量天然巖石中富含近似弧形裂隙現象。在外來荷載的作用下，這些已經存在的裂隙尖端附近很容易萌生新的裂紋，新生裂紋的擴展可能會導致巖石工程失穩[1-5]。近年來國內外眾多學者針對直線型缺陷巖石力學特性開展了大量的研究工作，取得了一系列研究成果[6-12]，然而對于含非直線型裂隙巖石力學特征研究涉及較少，相關研究鮮有報道，因此開展研究非直線型缺陷巖石的力學問題對巖石工程的穩定控制具有重要意義。

國內外巖石力學研究學者通過在類巖石和真實巖石材料中預制不同參數的直線型裂隙，研究裂隙參數對巖石裂隙力學特征的影響。NEMAT等[13]分別對單軸和雙軸壓縮條件下直線型裂隙相互影響開展試驗研究，研究表明預制裂隙傾角是控制尖端主生裂隙擴展方向和試樣破壞模式的有效參數之一，并利用斷裂力學分析了在整體遠場壓縮作用下預制直裂紋的平面擴展機制，對裂紋生長過程的各種參數進行了量化。WONG等[14]在類巖石材料中預制平行裂隙，通過單軸壓縮研究裂紋貫通模式及峰值強度，提出了含平行裂隙缺陷試樣的破壞規則。WONG和CHAU等[15]分析了單軸壓縮下斷續雙裂隙大理巖的強度和裂紋擴展特征，得到裂隙傾角對試樣破壞模式的影響規律。楊圣奇[16]對斷續三裂隙砂巖試樣進行了單軸壓縮試驗，通過照相測量技術研究了不同裂隙傾角對砂巖強度和裂紋擴展的影響規律，并給出了三裂隙砂巖試樣宏觀變形特性與裂紋擴展過程之間的關系。YANG等[17-18]分析了預制斷續單裂隙脆性砂巖的力學特征，探討了裂隙長度和裂隙傾角對脆性砂巖強度和變形參數、AE分布規律以及裂紋擴展機制的影響。熊飛等[19]通過對含尖端相交裂隙砂巖試樣進行單軸壓縮試驗，研究了2條相交裂隙分布方向角β和夾角α對砂巖強度、變形及破裂演化特征的影響，并利用聲發射記錄了試樣加載過程中的聲發射特征，在宏觀裂紋的起裂、擴展和貫通過程中都會產生明顯的AE事件。

數字照相和聲發射技術作為監測裂紋擴展規律重要技術手段，已經廣泛應用于巖石力學研究領域。NGUYEN等[20]采用數字照相量測技術，研究了平面應變條件下斷續裂隙Neapolitan凝灰巖的裂紋擴展特征，加強了對軟巖中裂紋擴展機制的理解;YIN等[21]在花崗巖中預制表面裂隙，并借助數字散斑相關技術研究了不同巖橋傾角的平行裂隙試樣中裂紋貫通模式以及應變場變化規律。在數值模擬和理論分析方面也取得了大量的研究成果，XIE等[22]利用聲發射儀對層狀巖鹽單軸壓縮全過程進行數據采集，結合分形理論，提出了一種分析巖石損傷過程中AE數分形性質的方法。

以上文獻針對含直線型裂隙缺陷砂巖試樣的力學特性進行了大量的研究工作，眾多研究表明含預制裂隙缺陷巖石強度會明顯劣化，裂隙的形態、大小、位置和方向對巖石的破壞演化過程起著至關重要作用。然而在自然界中，巖石中的裂隙形狀并不規則，除了前人研究的裂隙形態外還含有大量的非直線型裂隙。目前已經有學者開展相關方面的研究工作，MA等[23]通過3D打印技術，在材料中設置正弦裂隙，通過單軸壓縮試驗研究傾斜角度和有效曲率對預制裂紋的影響，研究認為當有效曲率小于2/7.5時，正弦裂紋的開裂以尖端開裂的形式為主;當有效曲率大于2/7.5時，裂紋起裂以非尖端裂紋形式出現。但針對非直線型巖石力學相關特征研究還不夠全面，基于此筆者對含預制弧形裂隙砂巖進行室內單軸壓縮，研究弧形裂隙的γ(弧形拱頂高度a與弦長b/2比值)對砂巖基本力學參數、聲發射特征、破裂演化過程及破壞模式的影響規律，并探討弧形裂隙尖端裂紋擴展力學機制。

1 試 驗

1.1 試樣制備

本試驗所需黃砂巖巖樣采自山東臨沂市，該類巖石自然狀態下呈淺黃色，質地較為致密均勻，表面無孔洞裂隙缺陷，主要成分為石英和長石，平均密度為2.16 g/cm3。

參照前人試樣制作方法，本文對大塊巖樣進行切割打磨，制作成尺寸為(160±2) mm×(80±2) mm×(30±2) mm長方體板狀試樣。利用高壓水射流切割機試樣中心切割出弦長b為40±1 mm，拱高a分別為2，5，8，12，16和20 mm，其誤差值均在-1～+1 mm內，試樣加工如圖1所示。為減小試樣離散性對試驗數據分析影響，每種試樣制作2塊，完整試樣2塊，共計14塊試樣。

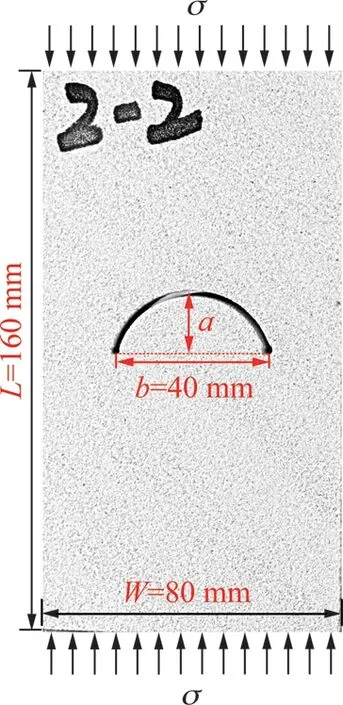
圖1 試樣及弧形預制裂隙幾何形態示意Fig.1 Diagram of the arc prefabricated fissure in the sandstone sample

1.2 試驗設備

試驗系統包括加載系統和數據采集系統如圖2所示，加載系統為中國礦業大學YNS-2000型電液伺服試驗機，該試驗機提供的荷載為0～2 000 kN，加載方式為位移控制加載，加載速度為0.02 mm/min，在進行單軸壓縮試驗前，為減小試樣端部摩擦效應，在試樣與加載板之間均勻涂抹一層凡士林。試驗數據采集系統主要包括應力應變數據采集、DS2聲發射數據采集系統和數字圖像采集系統，數字圖像采集利用高速攝像機對試樣的加載破裂演化過程進行實時采集。

圖2 試驗加載及數據采集系統Fig.2 YNS2000 electro-hydraulic servo test machine and the data acquisition system

2 試驗結果分析

2.1 軸向應力-應變曲線

單軸壓縮作用下2個完整黃砂巖試樣的應力-應變曲線如圖3(a)所示，2個完整試樣的峰值強度、峰值應變、平均彈性模量和割線模量的平均值分別為47.94 MPa，10.20×10-3，57.4 GPa和40.9 GPa，離散系數分別為1.42×10-2，3.9×10-2，2.6×10-2和5.4×10-2。由此可以看出本文所選用的黃砂巖均質性較好，力學參數離散性較小，適合對預制弧形裂隙砂巖力學特性進行定量研究分析。

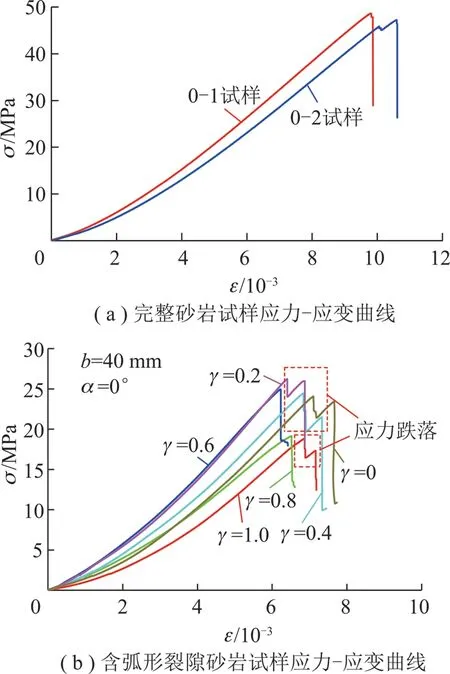
圖3 完整黃砂巖和含弧形裂隙砂巖試樣應力-應變曲線Fig.3 Stress-strain curves of the intact and arc fissures sandstone samples

完整試樣應力-應變曲線分孔隙裂隙壓密段、彈性變形至微彈性裂隙穩定發展階段、非穩定破裂發展階段、破裂后階段。從圖3(a)可以看出軸向壓力在0～10 MPa內2個試樣均處于孔隙裂隙壓密階段表現出明顯的非線性特征，該段σ-ε曲線呈現比較明顯的上凹型，說明完整的黃砂巖內部的微裂紋和孔洞發育比較豐富，此階段主要是微裂紋與微孔洞閉合引起的;隨著位移的增加當軸向應力超過10 MPa后，試樣σ-ε曲線進入線彈性階段，此階段軸向應力與軸向應變之間呈現近似直線性關系。0-2號試樣軸向應力達到45.84 MPa(對應軸向應變為10.06×10-3)出現首次應力跌落，應力跌落至45.45 MPa(對應軸向應變為10.07×10-3)，應力跌落幅度為0.39 MPa。0-1號試樣在峰值強度前未出現明顯的應力跌落現象，當達到峰值強度時，試樣內部承載結構遭到整體破壞，試樣失去承載能力，應力迅速跌落至0。曲線在到達峰值應力之前基本未發生應力跌落，仍保持較好的線性特征，沒有明顯的屈服階段，說明黃砂巖試樣的脆性特征較為顯著。

不同γ試樣應力-應變曲線如圖3(b)所示，由圖可看出:與完整黃砂巖試樣應力-應變曲線相比，γ=0，0.2，0.4和1.0四種弧形裂隙缺陷試樣峰值強度后均有不同程度的應力跌落現象，表明試樣峰值強度后仍具有一定的承載能力，弧形裂隙缺陷砂巖試樣隨著γ的增大，應力跌落幅度逐漸降低，峰后試樣的承載能力逐漸降低。γ=0時，試樣首次應力跌落點處軸向應力和軸向應變分別為24.95 MPa和6.93×10-3，分別為其峰值強度和峰值應變的94.43%和100.93%，隨后應力出現反復的升降現象;γ=0.6和0.8試樣達到峰值強度后并未出現應力跌落現象，而是試樣整體失去承載能力，軸向應力跌落至0;γ=1時，試樣首次應力跌落點處軸向應力和軸向應變分別為16.55 MPa和6.94×10-3，分別為其峰值強度和峰值應變的87.92%和101.02%，隨后出現應力上升后迅速下降至0的過程，與γ=0試樣相比首次應力跌幅較大。由此可見，γ對弧形裂隙黃砂巖試樣的峰后特征具有重要的影響作用，γ越大，試樣的峰后承載能力就越弱。

2.2 力學參數特征

由圖4(a)～(c)可以看出與完整黃砂巖試樣相比，單軸壓縮作用下弧形裂隙缺陷砂巖力學參數出現了明顯的劣化現象。圖4(a)表明隨著γ的增大，弧形裂隙砂巖峰值強度出現總體劣化趨勢，試樣峰值強度僅為完整試樣平均峰值強度的38.67%～54.34%。在γ=0.4～0.6內峰值強度劣化程度處于穩定狀態，但當γ在0.6～0.8內峰值強度劣化程度加劇，峰值強度由24.33 MPa降至20.13 MPa，降幅達17.27%。當γ=1時，試樣平均峰值強度最小，其值為18.99 MPa，表明γ在0.6～1.0內對試樣峰值強度的劣化最為明顯。由圖4(b)可以看出試樣峰值應變為完整試樣平均峰值應變的65.21%～70.12%。與試樣峰值強度劣化趨勢相似，峰值應變總體表現為隨γ值增大而呈減小趨勢。當γ=0時，試樣峰值應變最大，其值為6.97×10-3;當γ=0.6時，試樣峰值應變為6.64×10-3。可見在γ=0～0.6內，試樣峰值應變劣化程度較小基本趨于穩定。當γ=0.8和1.0時，試樣峰值應變分別降至為6.49×10-3和6.37×10-3，與γ=0.6的試樣峰值應變相比分別減少了0.35×10-3和0.47×10-3。由圖4(c)和(d)可以看出，隨著γ值的增加，弧形裂隙砂巖試樣的平均模量和割線模量均出現先增大后減小趨勢。弧形裂隙砂巖試樣的平均彈性模量和割線模量分別為完整試樣平均值的65.70%～91.00%和49.42%～70.30%，γ值從0增大到1，試樣的平均彈性模量由53.6 GPa降低到38.7 GPa，降幅為27.80%，割線模量由30.3 GPa減小到21.3 GPa，降幅為29.70%。

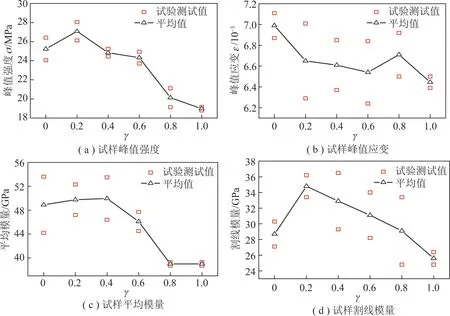
圖4 不同γ值試樣基本物理力學參數Fig.4 Stress-strain curves and mechanical parameters

2.3 試樣破壞演化及破壞形態

2.3.1聲發射與破裂演化特征

巖石材料在外力作用下內部裂紋萌生和擴展引起的能量釋放現象稱為聲發射，聲發射信號特征能實時反映巖石內部裂紋的動態演化過程[24]。根據巖石試件在受壓過程中聲發射信號特征(能量計數和振鈴計數)，可將黃砂巖試樣應力-時間曲線劃分為5個階段:① 壓密階段(OA)，在這個階段中巖石內部裂紋閉合導致較小振幅的聲發射產生，但由于巖石各向異性、非均勻性，聲發射事件比較雜亂;② 彈性階段(AB)，產生少量的聲發射;③ 穩定破裂階段(BC)，聲發射多為突發型的，比彈性階段聲發射信號強度、事件總數有所提高;④ 非穩定破裂階段(CD)，此段聲發射活動急劇增多;⑤ 峰后階段(DE)，此階段能量計數率達到峰值，特別是在峰后拐點處聲發射信號基本上達到峰值[25]。

圖5為不同γ值試樣在單軸壓縮下聲發射特征，由圖5(a)～(f)可以看出在初始壓密階段，γ=1試樣聲發射現象較為明顯，累計聲發射次數明顯增大，其余試樣聲發射現象并不明顯，累計聲發射次數呈緩慢增加趨勢。這是由于弧形裂隙γ越大，裂隙尖端處受到的集中應力也就越大，在壓密過程中除了部分礦物顆粒摩擦碰撞、微裂隙的咬合產生少量聲發射外，主要是尖端處開始產生拉伸破裂產生密集聲發射事件。

在彈性變形階段試樣的聲發射事件并不明顯，沒有較大的聲發射事件發生，累計聲發射曲線幾乎處于一個緩慢上升狀態，表明該階段6種試樣內部并未發生大的破裂過程，沒有明顯的能量釋放，而是聚集了較多的彈性能量。

在峰值強度前試樣進入非穩定破壞階段，試樣內部尖端處裂紋擴展迅速，聲發射活動變得非常活躍，在首次應力跌落即試樣初次破裂時，試樣釋放大量能量，聲發射次數顯著增加，累計聲發射曲線陡然上升。在試樣完全破壞的瞬間聲發射數達到最大值，表明弧形預制裂隙黃砂巖試樣依然具有較大的脆性，試樣整體破壞的瞬間釋放大量能量。由圖5還可以看出，隨著γ值的增大累計聲發射數整體減小趨勢，γ為0.8時，累計聲發射事件數最小，γ為0.2時，累計聲發射事件數最大。這也表明γ值越大，即弧形弧度越大越容易發生拉伸破壞。

屈服強度是試樣抵抗其微量塑形變形的應力，屈服點C的確定是研究固體力學機械性的一項重要評價指標。由圖5(a)～(f)可知砂巖壓縮過程中階段劃分的A，B，C三個分界點不易從試樣強度曲線上判斷，但根據聲發射信息可較好的進行識別，識別過程需根據振鈴計數、能量計數的特征判斷，并同時參考應力-時間的曲線進行綜合判定，筆者根據MARTIN[26]等提出的計算方法，定義單軸加載條件下C點為試樣屈服點，C點對應的強度為試件屈服強度。

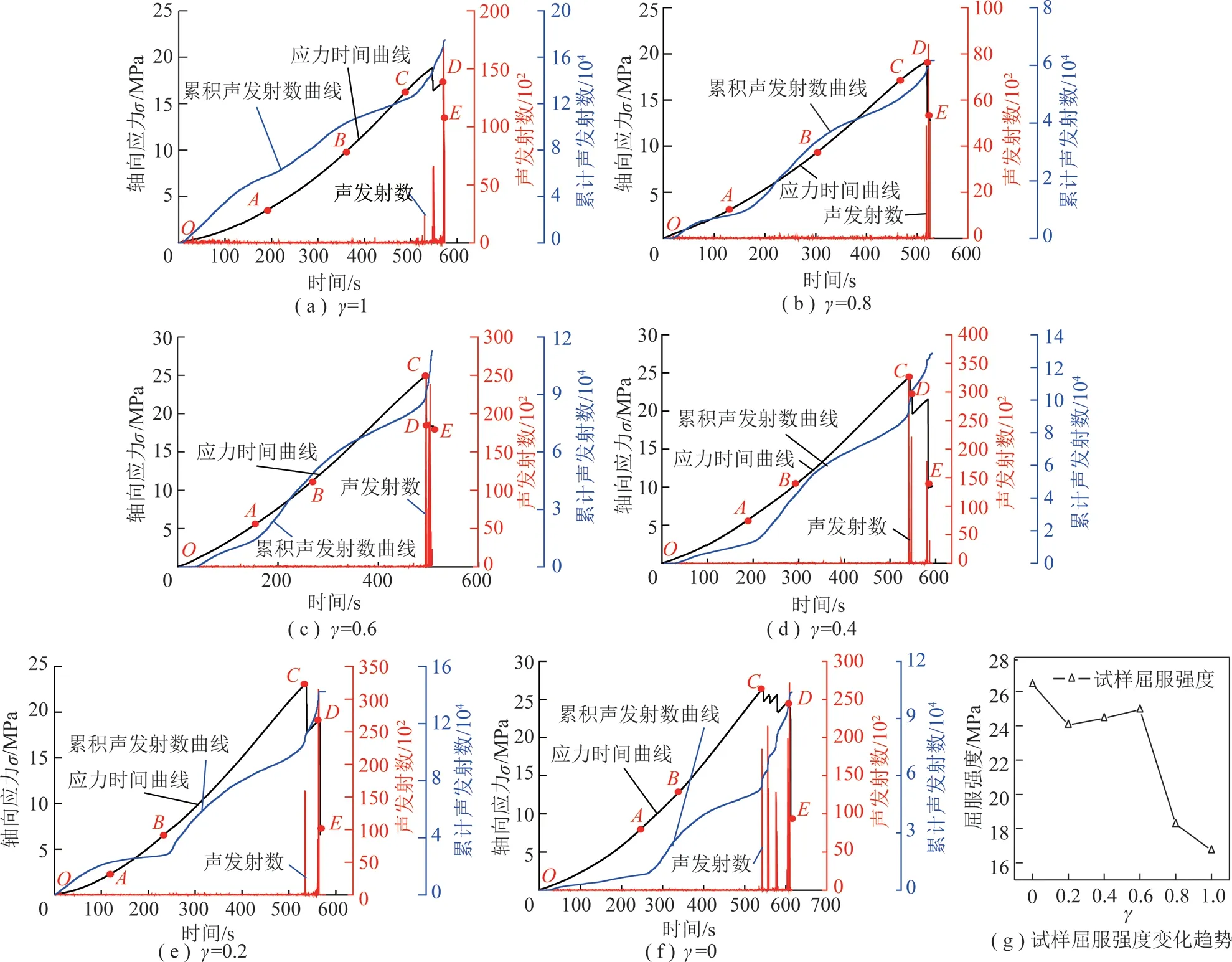
圖5 不同γ值試樣聲發射分布特征和屈服強度Fig.5 AE distribution characteristics and yield strength

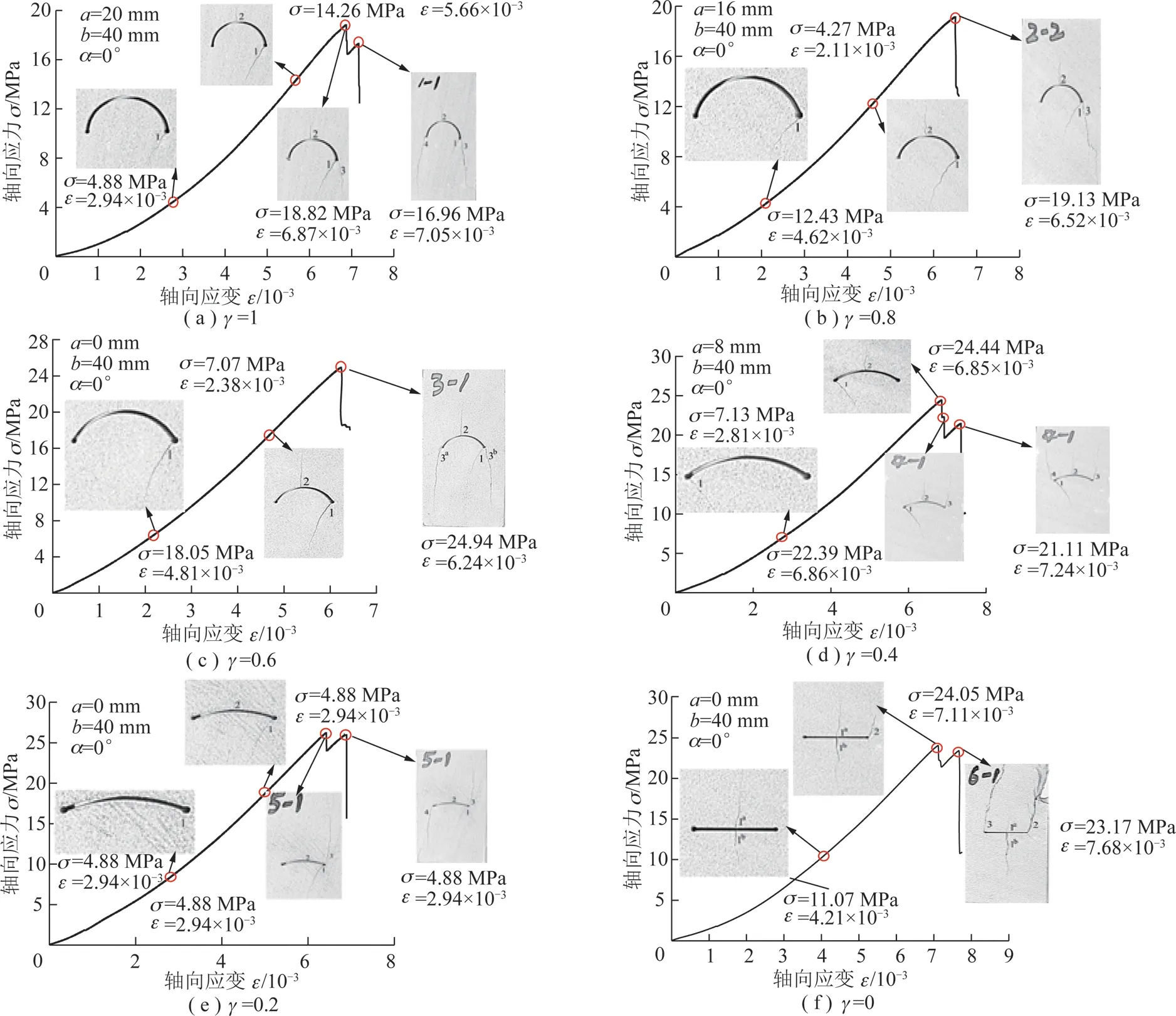
圖6 不同γ值試樣破裂演化過程Fig.6 Fracture evolution process of the sandstone samples

圖5(g)表明試樣屈服強度隨γ增大呈現先減小后緩慢增大最后又急劇減小趨勢，γ=1試樣屈服強度最小為16.72 MPa，γ在0.2～0.6試樣屈服強度趨于穩定，γ在0.6～0.8試樣屈服強度陡然減小，其強度由24.94 MPa降至18.26 MPa，下降了6.68 MPa，降幅為26.78%。γ=0時試樣屈服強度達到最大值為26.42 MPa。可見，在單軸壓縮作用下γ對試樣的屈服強度也具有重要影響作用。

從弧形裂隙缺陷砂巖初始破壞形式可知，試樣的破壞主要是從裂隙一側尖端處發起，隨后弧形頂部中間位置處產生縱向拉伸裂隙。隨著軸向應力增加，次生尖端拉伸裂紋萌生并且持續擴展，次生裂紋與自由面貫通導致試樣整體結構破壞，如圖6所示。由于篇幅原因，本文僅選取γ=1的試樣對弧形裂隙缺陷砂巖試樣的破裂演化特征進行分析。

在軸向壓力達到4.88 MPa，對應的軸向應變為2.94×10-3時，預制弧形裂隙右側尖端處出現細微的拉伸裂紋1，并伴隨較為強烈的聲發射現象，尖端處拉伸裂紋1的擴展范圍如圖6(a)所示。當軸向應力達到14.26 MPa，對應的軸向應變為5.66×10-3時，拉伸裂紋1持續擴展，同時弧形預制裂紋拱頂出現平行于加載方向的微小拉伸裂紋2，左側尖端出現輕微剝落現象并伴隨強烈的聲發射現象，但應力并未跌落。當軸向應力達到峰值強度18.82 MPa，對應的軸向峰值應變為6.87×10-3時，裂紋1和2繼續擴展，預制裂隙的右側尖端出現張拉裂紋3，隨后軸向應力由18.82 MPa跌落至16.48 MPa。當軸向應力達到16.96 MPa時，對應軸向應變為7.05×10-3時，裂紋1寬度出現開度變窄現象，裂紋2并未出現持續擴展，這種現象是由于處于同一承載結構中的裂紋3的持續擴展和新的張拉裂紋4的出現造成。隨著軸向應力的增大，拉伸裂紋3和裂紋4與試樣自由面貫通，試樣整體失去穩定導致最終破壞。

通過試樣破裂演化特征可知，預制弧形裂隙的破壞大部分是從底部尖端脆弱區發起，分析原因是由于該處是應力集中區，當應力大于其抗拉強度時，該處產生微小的張拉裂紋。隨著軸向應力增大，弧形裂紋拱頂部位出現張拉裂紋。但試樣的最終破壞并不是由初始尖端裂紋和非尖端裂紋的擴展所致，而是由次生尖端裂紋的擴展并與自由面貫通造成。γ的不同對弧形裂隙缺陷試樣的破壞形式具有重要影響，γ越大，試樣內弧形裂紋尖端處越容易產生張拉裂紋。

2.3.2初始起裂形式與起裂應力

巖石材料具有非均質、非連續及各向異性特點，在加載過程中會出現局部應力集中，當應力超過該區域的材料強度時，就會發生開裂破壞[18]。試樣在加載過程中的起裂位置和起裂應力能夠反映巖石材料的非均質性和內部缺陷的結構性。表1給出了試樣的初始起裂應力、起裂時的應變及初始起裂位置。可以看出預制弧形裂隙缺陷砂巖在單軸壓縮作用下，初始起裂是以弧形裂隙尖端處的拉伸破壞開始為主，出現一條與加載方向具有一定夾角的初始裂紋，隨后在弧形拱頂出現非尖端拉伸裂紋。隨著軸向應力的增大，裂紋逐漸擴展同時出現次生裂紋，次生裂紋擴展并與自由面貫通導致試樣出現整體失穩破壞。

表1 試樣起裂應力應變和起裂位置
Table 1 Stress and the position of the initial fractureof sandstone

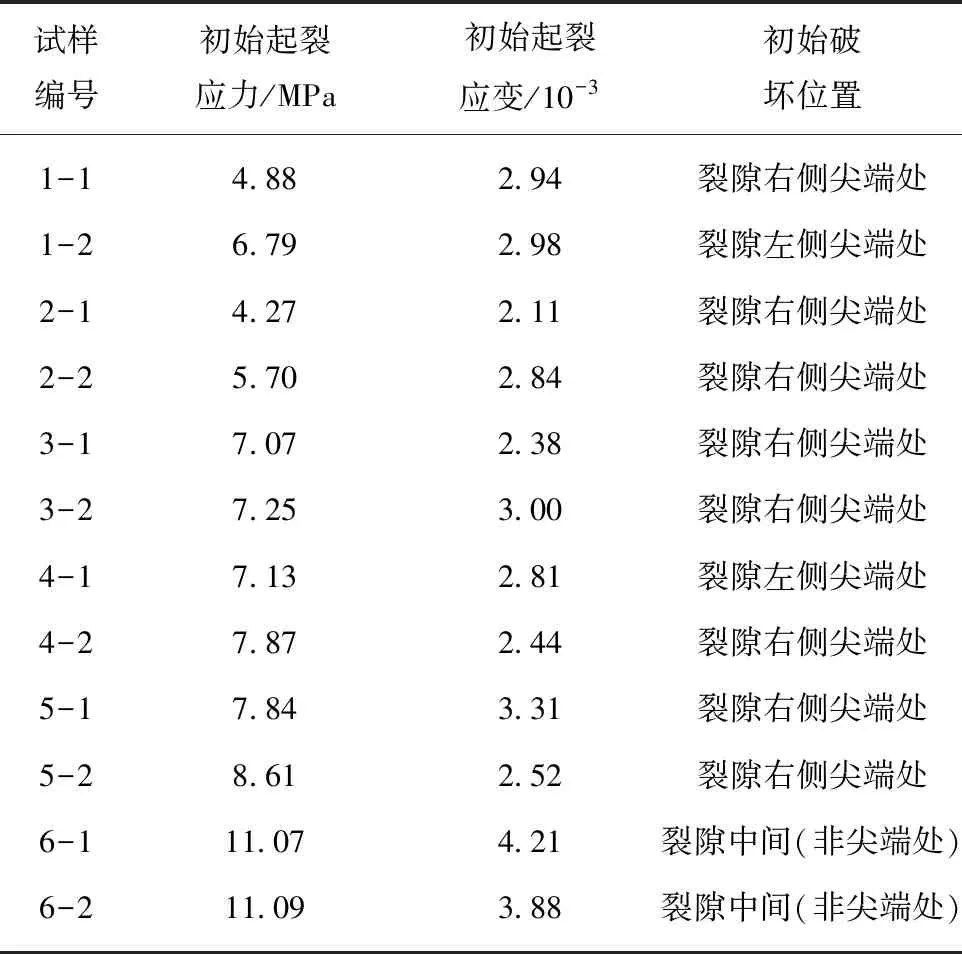
試樣編號初始起裂應力/MPa初始起裂應變/10-3初始破壞位置1-14.882.94裂隙右側尖端處1-26.792.98裂隙左側尖端處2-14.272.11裂隙右側尖端處2-25.702.84裂隙右側尖端處3-17.072.38裂隙右側尖端處3-27.253.00裂隙右側尖端處4-17.132.81裂隙左側尖端處4-27.872.44裂隙右側尖端處5-17.843.31裂隙右側尖端處5-28.612.52裂隙右側尖端處6-111.074.21裂隙中間(非尖端處)6-211.093.88裂隙中間(非尖端處)

由圖7(a)可知，γ值對試樣起裂應力具有重要的影響作用，隨著γ值的增大，試樣起裂應力呈總體減小趨勢，γ=0.8時試樣的平均起裂應力最小，其值為4.99 MPa，表明該試樣最容易發生初始破壞。γ=0時試樣的平均起裂應力值為11.08 MPa，平均起裂應力值最大。其中，γ值在0～0.2，平均起裂應力值由11.08 MPa降至8.23 MPa，降低了2.85 MPa，降低幅度達25.72%。γ=0.2～0.6，平均起裂應力由8.23 MPa降至7.15 MPa，降低了1.08 MPa，降幅為13.12%，由此可見，試樣的γ在該范圍內，起裂應力值變化并不明顯，對試樣初始破壞影響較小。γ=0.6～0.8，平均起裂應力出現先減小后增大趨勢。由圖7(b)可以看出γ值對試樣起裂應變也具有重要的影響，試樣相應起裂應變與起裂應力變化趨勢基本一致也呈現出先減小后增大的波動趨勢，γ=0.8時試樣的平均起裂應變最小，其值為2.48×10-3。

2.3.3試樣破壞形態分析

由圖8可以看出，試樣的最終破壞模式以拉伸破壞為主,圖8中，T為拉伸裂紋，S為剪切裂紋。通過圖9(a)～(e)可以發現，試樣破壞大部分是從應力集中區的弧形尖端發起，試樣在軸向應力達到起裂應力時，首先在一側弧形尖端處產生與豎向應力有一定夾角的微小拉伸裂紋1，隨著軸向應力的增大，拉伸裂紋1持續擴展且開度增大，同時弧形裂隙弧頂出現拉伸裂紋2。在應力達到一定強度時，裂隙尖端處順序出現較大拉伸裂紋3和4，在裂紋3和4擴展的過程中裂紋1開度變小。試樣最后的破壞是裂紋3和4與自由面的貫通造成的拉伸破壞。試樣在破壞的瞬間釋放的大量彈性能導致巖塊出現折斷現象，如圖8(a)～(c)和(e)～(f)在試樣破壞的過程中出現了1～2個的折斷破壞現象，然而圖8(d)試樣在失去承載能力時并未發生明顯的折斷現象，破壞后的試樣較為完整。

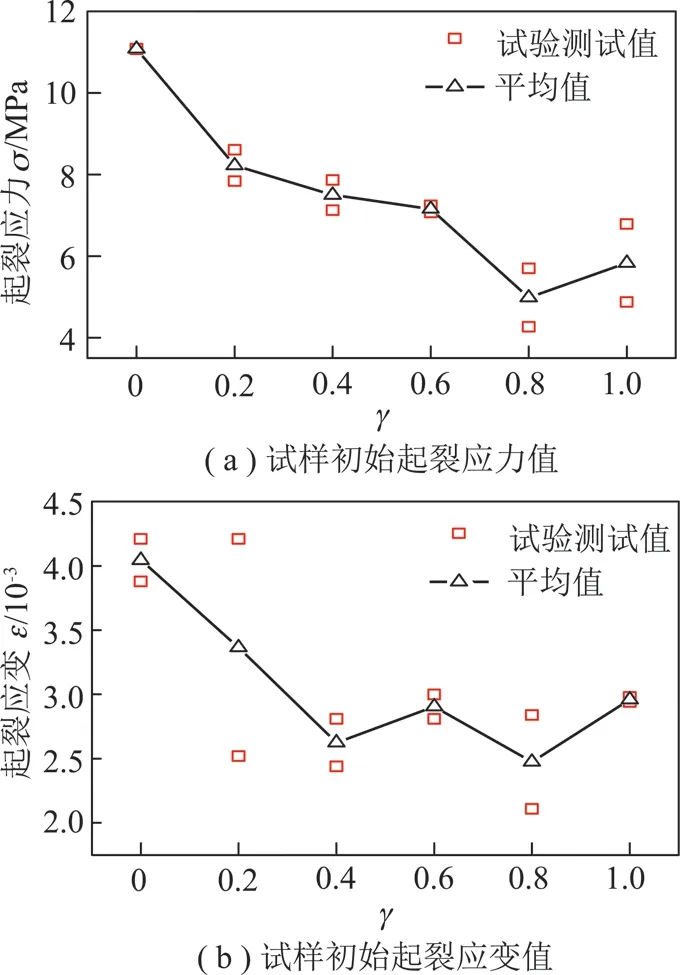
圖7 預制弧形裂隙單軸壓縮下起裂應力值和應變值Fig.7 Crack initiation stress and the strain of sandstone samples

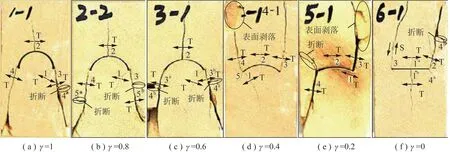
圖8 不同γ值試樣破壞形態Fig.8 Failure mode of the sandstone samples

圖8(f)即γ=0的試樣表明初始拉伸裂紋1a和1b同時萌生于直線型預制裂隙的中間位置處，裂紋1a和1b在裂隙兩側呈對稱分布，并且均近似平行于豎直加載方向。在軸向應力達到峰值強度時，裂隙右側尖端處出現拉伸裂紋2，同時出現應力跌落現象并伴隨巨大聲發射事件。隨著軸向加載的持續，拉伸裂紋2與自由面貫通，同時裂隙左側尖端處發生剪切破壞產生裂紋3，可見γ=0的試樣破壞模式為拉剪混合破壞。

3 裂紋擴展力學機制探討

任一種類型裂紋端部應力場分布規律是相同的[27]，其大小僅取決于應力強度因子KJ。因此本文通過建立如圖9所示弧形裂隙的力學模型來確定弧形裂隙尖端應力強度因子，該物理量可以表征裂紋端部應力場強弱以及斷裂韌性大小。假設黃砂巖中任意Z0點受集中荷載作用，預制圓弧形裂紋Z1Z2的圓心角為2β，弧形裂隙的半徑為r。弧形裂隙周圍應力場中可通過構建黎曼-希爾伯特問題后用標準復變函數法進行求解[28]。

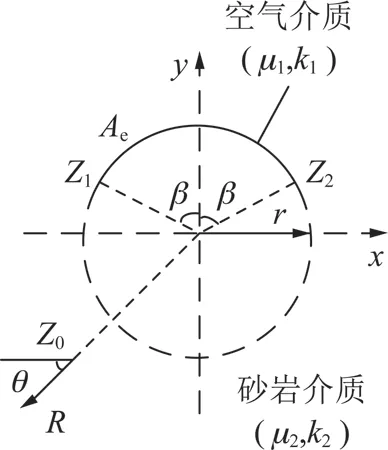
圖9 集中荷載作用下弧形裂隙Fig.9 Arc crack under concentrated load

可建立Kolosov-Muskhelishvili表達式如下:

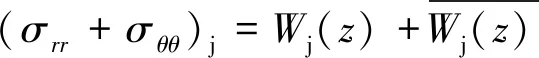
(1)

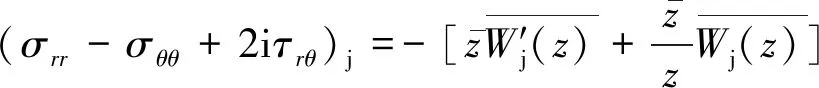
(2)

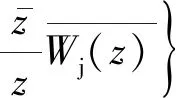
(3)

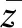
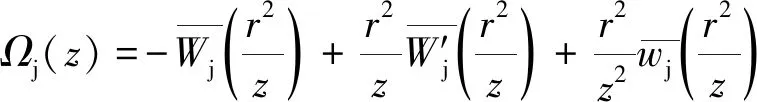
(4)

則可以證明:

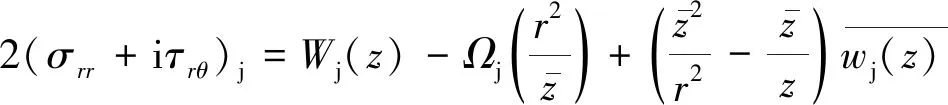
(5)

式中，r為質點到坐標原點的距離。

因為裂縫面無附著摩擦力從而引入了下面的黎曼-希爾伯特問題:

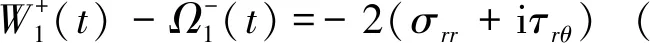
(6)

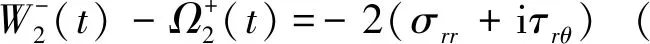
(7)

弧形裂隙兩介質交界面結合部分的應力和位移連續性需滿足如下要求:

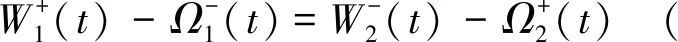
(8)

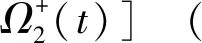
(9)

式中，μ1，μ2分別為空氣和砂巖介質的泊松比；k1，k2分別為空氣和砂巖介質的平面應力及平面應變。

Ac和Ab分別對應于2種介質交界面的開裂部分和黏結部分，式(8)和(9)可被視為在交界面結合部分從S+到S-的解析延拓，因此W1(t)和Ω1(t)可以用W2(t)和Ω2(t)來表示，因此，對于黃砂巖介質內潛能為

[W2(t)-Ω2(t)]++α[W2(t)-Ω2(t)]-=

-2(1+α)(σrr+iτrθ)

(10)

[W2(t)+αΩ2(t)]+-[W2(t)+αΩ2(t)]-=0

(11)

式中，

以上黎曼-希爾伯特問題可通過方程(12)和(13)解決:

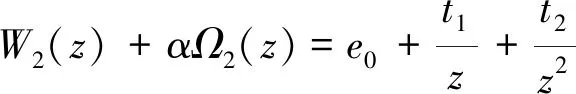
(12)

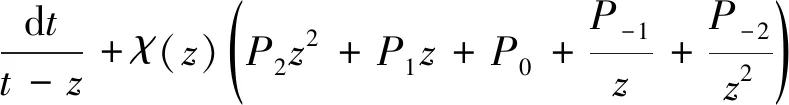
(13)

式中，e0為常數；t1和t2分別為弧形裂隙兩端的位置坐標；P0，P1，P2為羅朗展開式系數；P-1和P-2為與介質交界面法向相反的羅朗展開式系數。

式(13)中的χ(z)可由Plemelj方程解出:

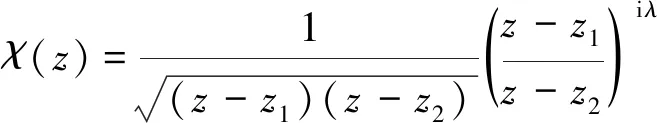
(14)

上式中當z→時，另外，

χ(z)在z→0和z→處的展開式如下:

χ(z)=F10(1+zF12+z2F13+…),z→0

(15)

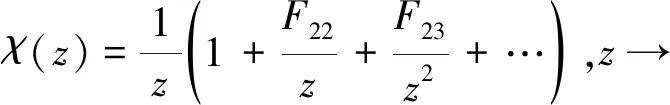
(16)

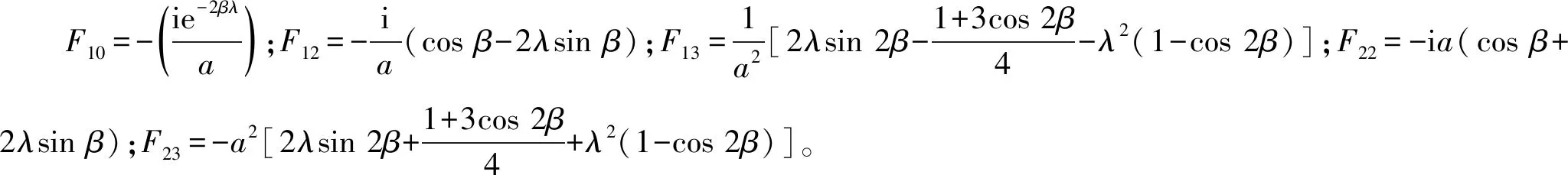
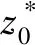
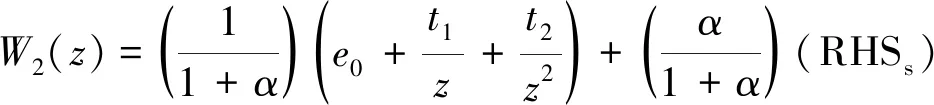
(17)

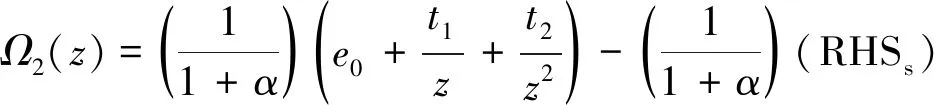
(18)

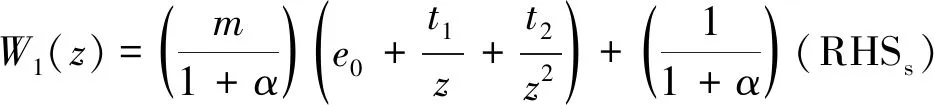
(19)

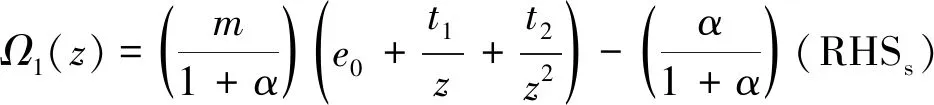
(20)

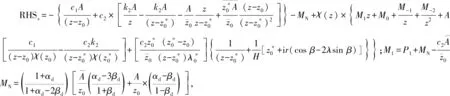
e0,t1,t2,M1,M0,M-1和M-2七個常量是由原點和無窮大處求解所得。根據文獻[29]定義了2種介質交界面裂紋的復應力強度因子為

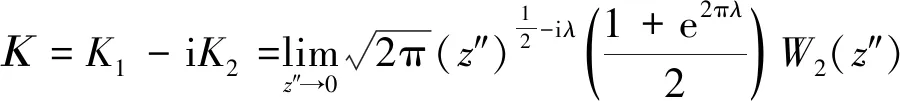
(21)

其中，λ=-lgα/(2π)；i為虛數單位;z″對應于z1處的新坐標系，該坐標系通過z=eiβ(z″-ir)進行轉換，如圖10所示。通過式(17)可求得交界面裂紋的復應力強度因子為

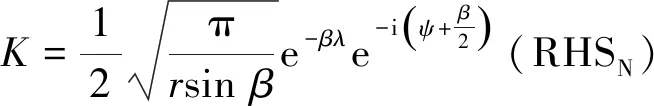
(22)

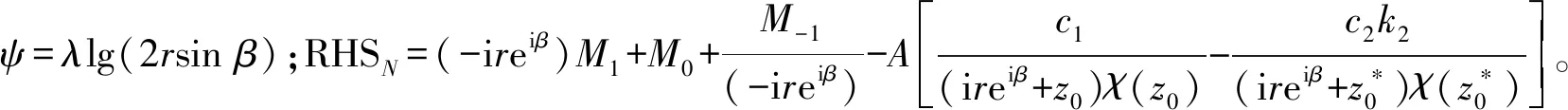
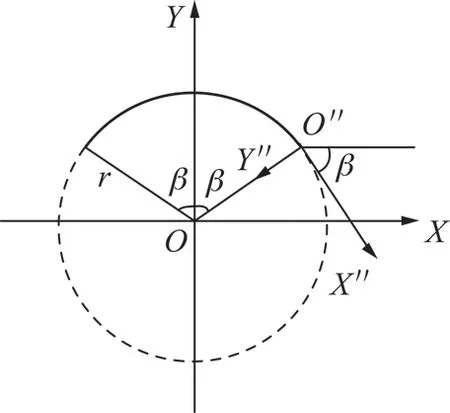
圖10 經過轉換后的新坐標系統O"Fig.10 Transformation to the new coordinate system at O"

通過交界面復應力強度因子可以看出弧形裂隙夾角β和半徑r影響裂隙尖端應力場分布，也是影響裂隙尖端起裂應力大小的重要因素，當γ=0→r=0 mm，β=0°;γ=0.2→r=52.0 mm，β=22.6°;γ=0.4→r=29.0 mm，β=43.5°;γ=0.6→r=22.67 mm，β=61.90°;γ=0.8→r=20.5 mm，β=77.3°;γ=1.0→r=20 mm，β=90°。把夾角β和半徑r代入式(22)可求出不同γ下的應力強度因子，由圖11可知，通過應力強度因子數值擬合曲線可以看出應力強度因子隨γ增大呈逐漸減小趨勢，這與試驗測得的初始起裂應力和應變值的變化趨勢基本吻合，表明弧形預知裂隙γ值越大尖端斷裂韌性越小，試樣越容易起裂。

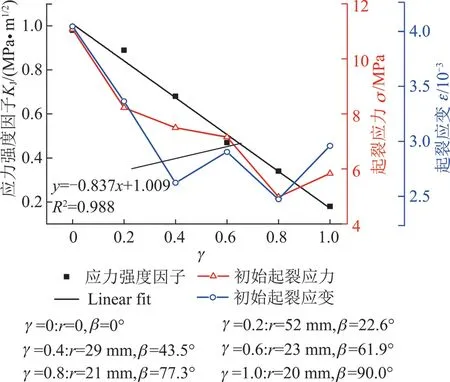
圖11 應力強度因子變化趨勢Fig.11 Change trend of stress intensity factor

4 結 論

(1)弧形裂隙缺陷砂巖試樣隨著γ的增大，峰后試樣的承載能力逐漸降低，試樣峰值強度、平均模量和割線模量出現總體減小趨勢。在γ=0～0.6峰值強度劣化程度處于穩定狀態，當γ為0.6～0.8時峰值強度劣化程度加劇，γ為1時，試樣峰值強度最小，這也表明γ在0.6～1.0對試樣峰值強度的改變影響因素最為顯著。

(2)隨著γ值的增大累計聲發射數呈整體減小趨勢，γ為0.8時，累計聲發射事件數最小，γ為0.2時，累計聲發射事件數最大。γ值對試樣起裂應力具有重要的影響作用，隨著γ值的增大，試樣起裂應力呈總體減小趨勢，γ=0.8時平均起裂應力值最小，試樣最容易發生初始破壞;γ=0時，試樣的平均起裂應力值最大，其值為11.08 MPa。試樣相應起裂應變也呈現出先減小后增大的波動趨勢。當γ=0時初始起裂裂紋萌生于直線型裂隙的中間位置;當γ=0.2～0.8時，裂紋萌生于預制裂隙尖端位置處。

(3)隨著γ的增大，試樣的破壞模式由拉剪混合破壞向拉伸破壞轉變，當γ=0時，試樣為拉剪破壞;當γ在0.2～1.0時，試樣為拉伸破壞。初始起裂裂紋擴展并不是導致試樣最終破壞的原因，次生裂紋的擴展與自由面貫通才是導致試樣整體破壞原因，試樣破壞瞬間釋放大量彈性能導致巖塊折斷和表面剝落現象。通過對含弧形裂隙裂紋擴展機制探討推導出應力強度因子表達式，并根據該表達式求出相應應力強度因子值，曲線擬合后發現其變化趨勢與試驗值變化趨勢基本吻合。

本文僅針對含弧形預制裂隙的γ對砂巖力學特征和破裂演化過程進行了研究，為了充分研究非直線型裂隙的對巖石力學影響，未來將通過改變加載方式和利用數值模擬等手段深入研究該含該類缺陷巖石的力學特征。