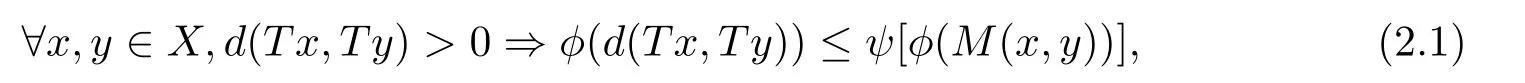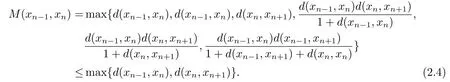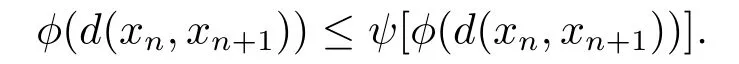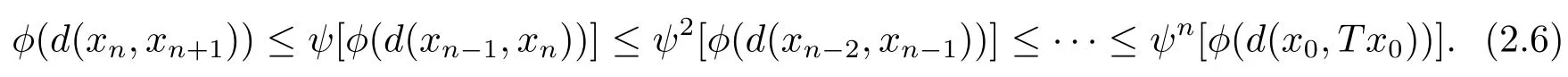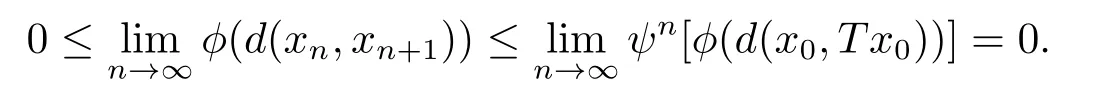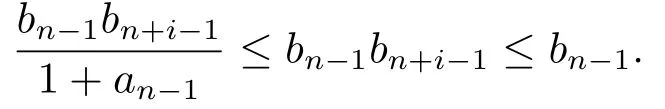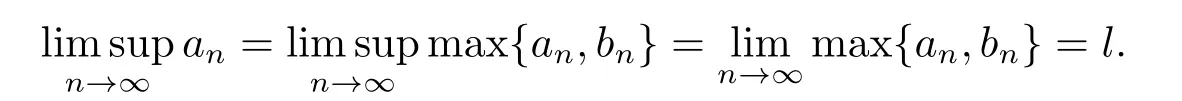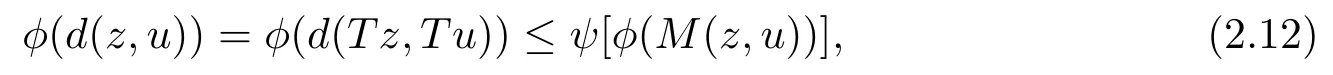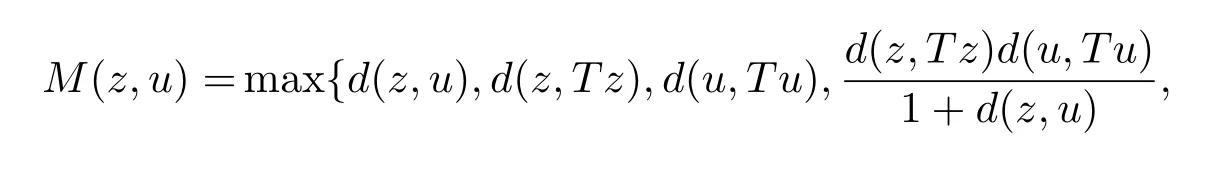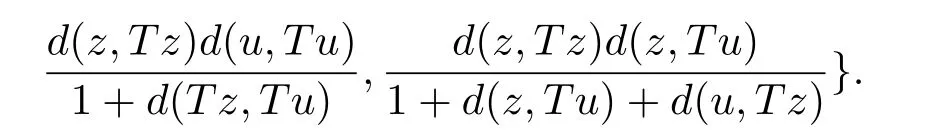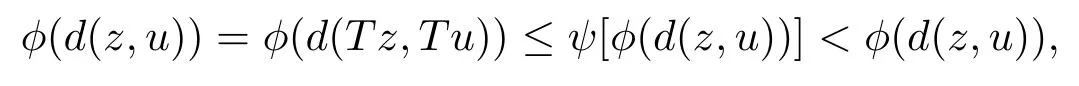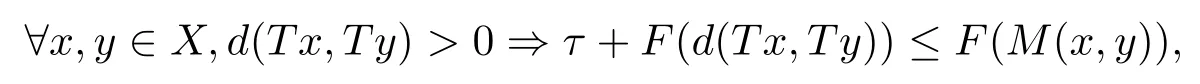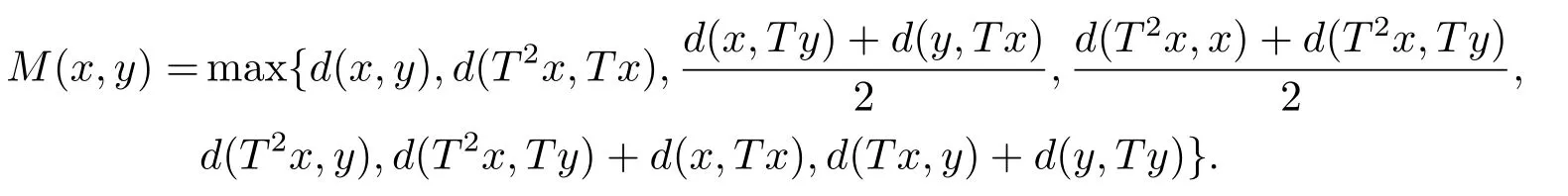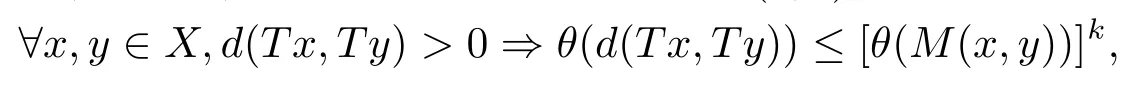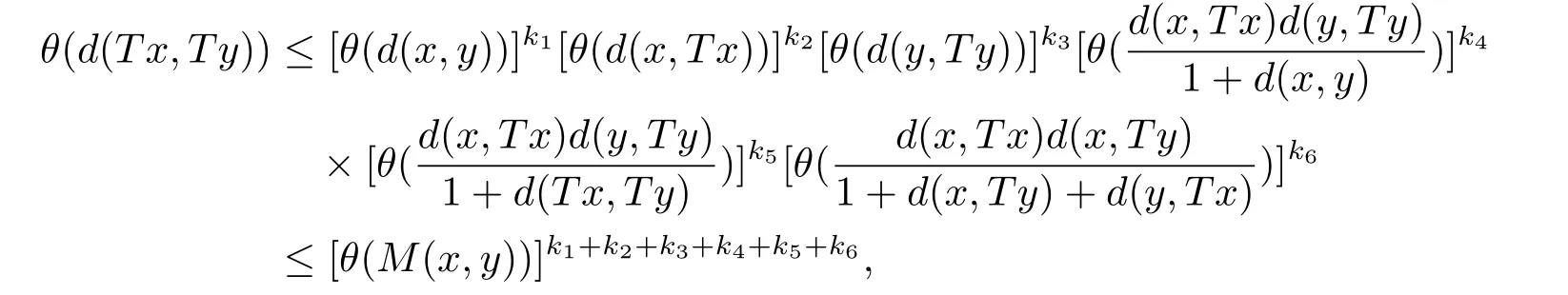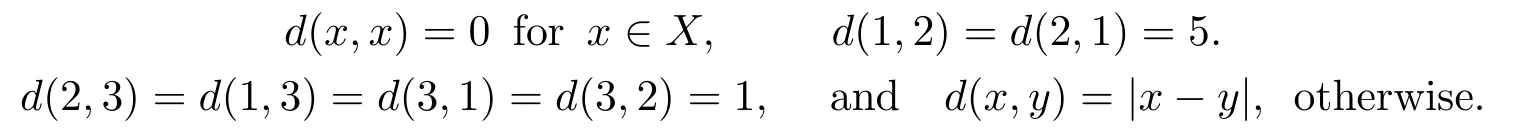Some Fixed Point Theorems in Complete ν-Generalized Metric Spaces
LIU Xianpeng(劉先鵬),JI Peisheng(紀培勝)
(School of Mathematics and Statistics,Qingdao University,Qingdao 266071,China)
Abstract: The contractive mapping of C-class function in the setting of metric space is generalized in this paper.The iterative method in complete ν-generalized metric space is used to prove the fixed point theorem of the C-class function on (ψ,?)-type contractive mapping.We also prove the fixed point theorems of the generalized F-type contractive mapping and generalized θ-type contractive mapping.
Key words: Fixed point; ν-generalized metric space;(ψ,?)-type contraction
1.Introduction and Preliminaries
The Banach contraction principle introduced by Banach[1]is one of the most important results in mathematical analysis.It is the most widely applied fixed point result in many branches of mathematics and it was generalized in many different directions[2?4].One of these generalizations was introduced by Branciari in 2000,where the triangle inequality was replaced by a so-called polygonal inequality.He introduced the concept ofν-generalized metric spaces as follows.
Definition 1.1[5?7]LetXbe a nonempty set andd:X ×X→[0,∞) be a mapping.Letν∈N.Then (X,d) is called aν-generalized metric space if the following hold:
1)d(x,y)=0 if and only ifx=y,for allx,y∈X;
2)d(x,y)=d(y,x),for everyx,y∈X;
3)d(x,y)≤d(x,u1)+d(u1,u2)+···+d(uν,y),for each set{x,u1,...,uν,y} ofν+2 elements ofXthat are all different.
Obviously,every metric space(X,d)is a 1-generalized metric space.A generalized metric space is also said to be a 2-generalized metric space.In [8],it shown that not every generalized metric space has a compatible topology.Indeed,only 3-generalized metric space has a compatible topology(see [9]).
Definition 1.2[5?7]Let (X,d) be aν-generalized metric space and{xn} be a sequence inX;
1) The sequence{xn} is said to be a Cauchy sequence ifd(xm,xn)→0 asm,n→∞;
2) The sequence{xn} is said to converge tox∈Xifd(xn,x)→0 asn→∞.
3) The sequence{xn} is said to converge toxin the strong sense if{xn} is a Cauchy sequence and{xn} converges tox.
The spaceXis said to be complete if every Cauchy sequence inXconverges.
A sequence in 2-generalized metric space may converge to more than one point and a convergent sequence may not be a Cauchy sequence(see[10]).A sequence may be convergent,but not in the strong sense.
Proposition 1.1[5]Let{xn} and{yn} be sequences in aν-generalized metric space(X,d) that converge toxandyin the strong sense respectively.Then

Branciari[11]also proved a generalization of the Banach contraction principle;however,the proof is not correct.When proving theorems onν-generalized metric spacesX,we may have to be careful,becauseXdoes not necessarily have the compatible topology(see [8-9]).
In 1997,Berinde[12]introduced the concept of comparison function.
Definition 1.3[12]A functionψ:(0,∞)→(0,∞) is called a comparison function if it satisfies the following:
1)ψis monotone increasing,that is,t1 2) limn→∞ψn(t)=0 for allt>0,whereψnstands for the nth iterate ofψ.Clearly,ifψis a comparison function,thenψ(t) Definition 1.4[13]Let?:(0,∞)→(0,∞) be a mapping satisfying the following conditions: (Φ1)?is non-decreasing,that is,for allt,s∈(0,∞),t (Φ2) for each sequence{tn}?(0,∞),limn→∞?(tn)=0 iff limn→∞tn=0; (Φ3)?is continuous. We shall denote byΦthe set of all functions satisfying the conditions (Φ1),(Φ2) and (Φ3). Lemma 1.1[13]Let?:(0,∞)→(0,∞) be a non-decreasing and continuous function with inft∈(0,∞)?(t)=0 and{tk}kbe a sequence in (0,∞).Then the following conclusion holds. Lemma 1.2[7]Let (X,d) be aν-generalized metric space and let{xn} be a sequence inXwith distinct elements (xn≠xmforn≠m).Suppose thatd(xn,xn+1),d(xn,xn+2),...,d(xn,xn+ν) tend to 0 asn→∞and that{xn} is not a Cauchy sequence.Then there existε>0 and two sequences{mk} and{nk} of positive integers such thatnk >mk >kand the following four sequences tend toεask→∞: Theorem 1.1[13]Let(X,d)be a complete metric space andT:X→Xbe a(ψ,?)-type contraction,that is,there exist?∈Φand a continuous comparison functionψsuch that where ThenThas a unique fixed pointz∈Xand the sequence{Tnx} converges toz. In this paper,we first prove the theorem of fixed point for (ψ,?)-type contraction in the setting of completeν-generalized metric spaces.We next prove the theorems of fixed point for generalizedθ-type contraction and generalizedF-type contraction. Definition 2.1Let(X,d)be a completeν-generalized metric space andT:X→Xbe a mapping.Tis said to be a generalized (ψ,?)-type contraction,if there exists a comparison functionψand?∈Φsuch that where Theorem 2.1Let(X,d)be a completeν-generalized metric space andT:X→Xbe a generalized(ψ,?)-type contraction.ThenThas a unique fixed pointz∈Xand the sequence{Tnx} converges toz. ProofLetx0be an arbitrary point inX.We construct a sequence{xn} such thatxn+1=Txn=Tn+1x0.IfTp?1x=Tpx,thenTp?1xwill be a fixed point ofT.So,without loss of generality,we can assume thatd(Tn?1x,Tnx)>0.From (2.1) we have where Now if max{d(xn?1,xn),d(xn,xn+1)}=d(xn,xn+1),then by (2.1) we have This implies that?(d(xn,xn+1)) This together with inequality (2.3) yields that Since?:(0,∞)→(0,∞),it follows from (2.6) that This implies that limn→∞?(d(xn,xn+1))=0.This together with (Φ2) and Lemma 1.1 gives Now,we claim that limn→∞d(xn,xn+i)=0,fori=2,3,4,···,ν. By (2.1),we have where From (2.4) and (2.5) we haved(xn,xn+1) Since limn→∞bn=0,there existsN0such thatbn <1 for alln>N0,so we have Similarly,we have Then we getM(xn?1,xn+i?1)≤max{an?1,bn?1}.Sinceψ(t) so we havean≤max{an?1,bn?1}. Sincebn Taking limit supremum in (2.8) by the property ofψ,we have which is a contradiction.Sol=0,that is, We will prove thatxn≠xn+j,for alln≥0,j≥1.Namely,ifxn=xn+jfor somen≥0 andj≥1,we havexn+1=Txn=Txn+j=xn+j+1,which implies that is a contraction.Thus,we obtain thatxn≠xmfor all distinctn,m∈N. In order to prove that{xn} is a Cauchy sequence,suppose that it is not.Then,by Lemma 1.2,using (2.7) and (2.9),we conclude that there existsε >0 and two sequences{mk} and{nk} of positive integers such thatnk >mk >kand the sequences (1.1) tend toεask→∞.Using (2.1) withx=xmk?1andy=xnk,one obtains where Taking the upper limit ask→∞in (2.10),we get?(ε)≤ψ[?(ε)],which is a contradiction withε>0.Thus,{xn} is a Cauchy sequence.By completeness of (X,d),there existsz∈Xsuch that Finally,we show thatTz=z.Arguing by contradiction,we assume thatTz≠ z.we have where On taking limit asn→∞in above inequation and using (2.11),we obtain This is a contradiction.HenceTz=z.This is thatzis a fixed point ofT. Now we prove thatzis the unique fixed point ofTinX.In fact,ifz,u∈Xare two distinct fixed points ofT,that is,Tz=z≠u=Tu,then it follows the assumption that where This together with (2.12) shows that which is a contraction.Hence,we havez=u,thuszis the uniqueness fixed point ofT. In 2014,Jleli and Samet[14]introduced the following notion ofθ-contraction. Letθ:(0,∞)→(1,∞) be a function satisfying the following conditions: (Θ1)θis non-decreasing; (Θ2)For each sequence{tn}?(0,∞),limn→∞θ(tn)=1?limn→∞tn=0; (Θ3)There existr∈(0,1) andl∈(0,∞]such that In the sequel we denote byΘthe set of all functions satisfying the conditions (Θ1)-(Θ3). Definition 2.2[14]A mappingTis said to be aθ-contraction if there existsθ∈Θandk∈(0,1) such that?x,y∈X,d(Tx.Ty)≠0?θ(d(Tx.Ty))≤[θ(d(x,y))]k. In this paper,we use the following condition instead of condition (Θ3). (Θ′3)Θis continuous on (0,∞). We denote by?the set of all functions satisfying the conditions (Θ1),(Θ2),and (). Theorem 2.2[13]Let (X,d) be a complete metric space andT:X→Xbe aθ-type contraction,that is,there existθ∈?andk∈(0,1) such that whereM(x,y)=max{d(x,y),d(x,Tx),d(y,Ty),12d(x,Ty),d(y,Tx)}.ThenThas a unique fixed pointz∈Xand the sequence{Tnx} converges toz. In 2012,Wardowski[15]introduced the following notion ofF-contraction. Definition 2.3[15]LetF:(0,∞)→R be a mapping satisfying: (F1)Fis non-decreasing,that is,for allt,s∈R,t (F2)for each sequence{tn}?(0,∞),limn→∞F(tn)=?∞if and only if limn→∞tn=0; (F3)there existr∈(0,1) such that limt→0+trF(t)=0. In the sequel we denote byFthe set of all functions satisfying the conditions (F1)-(F3). Definition 2.4[15]A mappingTis said to be aF-contraction if there existsτ >0 such that In this paper,we use the following condition instead of condition (F3). (F′3)Fis continuous on (0,∞). We denote byΓthe set of all functions satisfying the conditions (F1),(F2),and (F′3). Theorem 2.3[16]Let (X,d) be a complete metric space andT:X→Xbe aF-type contraction,that is,there existF∈Γandτ >0 such that where ThenThas a unique fixed pointz∈Xand the sequence{Tnx} converges toz. Theorem 2.4Let (X,d) be a completeν-generalized metric space andT:X→Xbe aθ-type contraction,that is,there existθ∈?andk∈(0,1) such that whereM(x,y) is given by (2.2).ThenThas a unique fixed pointz∈Xand the sequence{Tnx} converges toz. ProofDenote byψ(t)=ktand?:=lnθ:(0,∞)→(0,∞).It is easy to check that?∈Φ.Hence,we have lnθ(d(Tx,Ty))≤klnθ(M(x,y)). The conclusion of Theorem 2.4 can be obtained from Theorem 2.1. Definition 2.5Let(X,d)be a completeν-generalized metric space andT:X→Xbe a mapping.Tis said to be a generalizedJS-contraction whenever there are a functionθ∈?and positive real numbersk1,k2,k3,k4,k5,k6with 0 for allx,y∈Xwith. Corollary 2.1Let (X,d) be a completeν-generalized metric space andT:X→Xbe a generalizedJS-contraction.ThenThas a unique fixed point. Proof whereM(x,y) is given by (2.2).Supposingk=k1+k2+k3+k4+k5+k6,from Theorem 2.4,we obtainThas a unique fixed point. Theorem 2.5Let (X,d) be a completeν-generalized metric space andT:X→Xbe aF-type contraction,that is,there existF∈Γandτ >0 such that whereM(x,y) is given by (2.2).ThenThas a unique fixed pointz∈Xand the sequence{Tnx} converges toz. ProofDenoteψ(t)=e?τtand?:=eF:(0,∞)→(0,∞).It is easy to check that?∈Φ.Hence,we have eF(d(Tx,Ty))≤e?τeF(M(x,y)). The conclusion of Theorem 2.5 can be obtained from Theorem 2.1. Example 1LetX={0,1,2,3,4} andd:X ×X→[0,∞) be defined by: Note that (X,d) is a complete 3-generalized metric space which is not a generalized metric space since 5=d(1,2)>d(1,3)+d(3,4)+d(4,2)=4. LetT:X→Xbe defined by Defineψ:(0,∞)→(0,∞) byψ(t)=,and?:(0,∞)→(0,∞) by?(t)=.Clearly,ψ∈Ψand?∈Φ,Tis a generalized (ψ,?)-type contraction mapping.Now if{xn} is a sequence inXsuch thatxn→xasn→∞,forx∈{0,1,2,3} andy=4,we have Thus,all conditions of Theorem 2.1 are satisfied.Moreover,x=2 is a fixed point ofT.
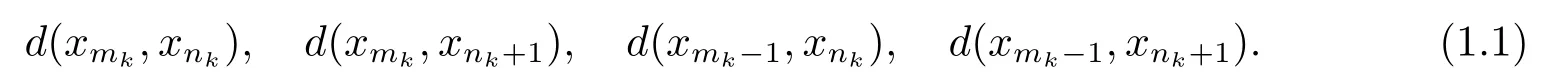

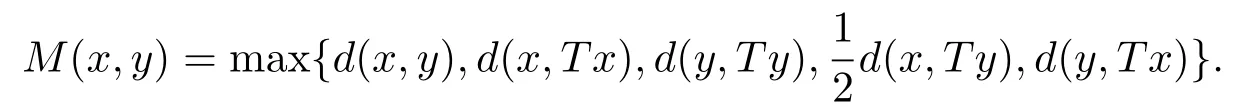
2.Main Result