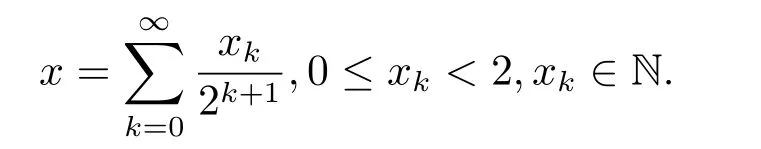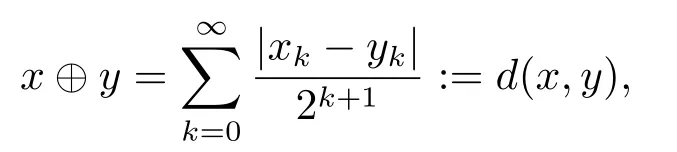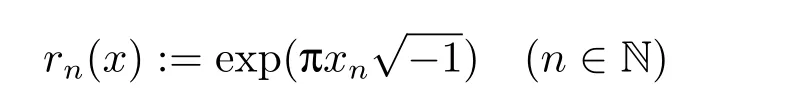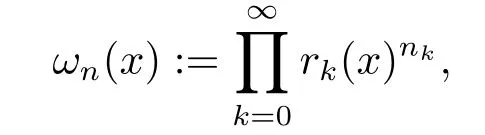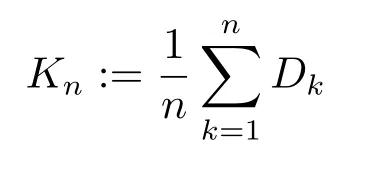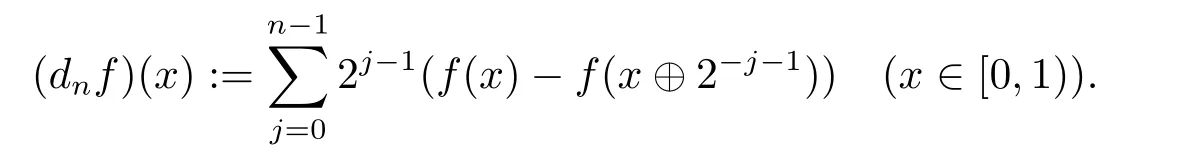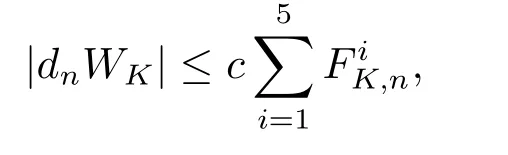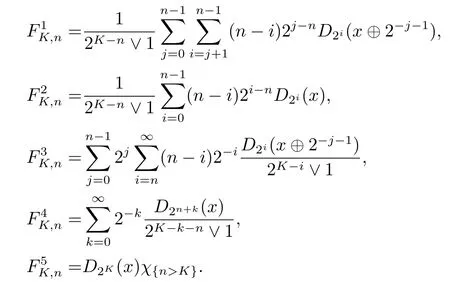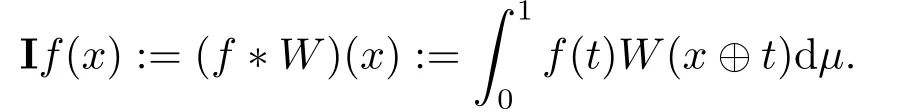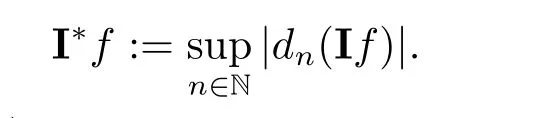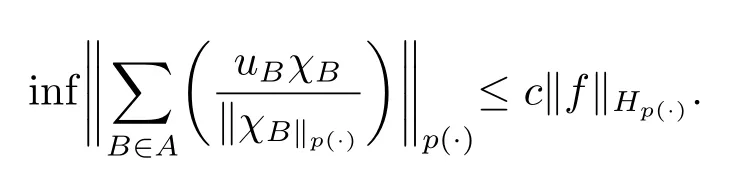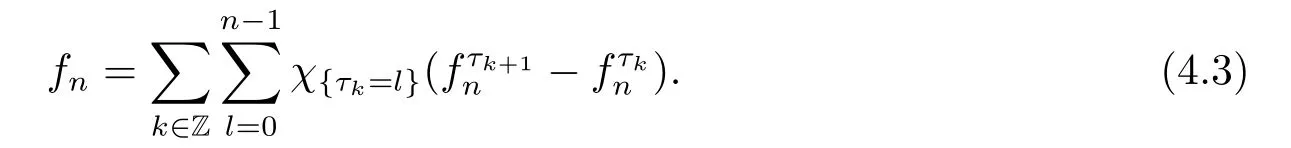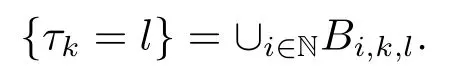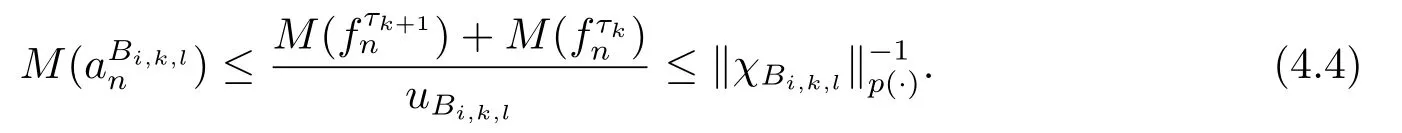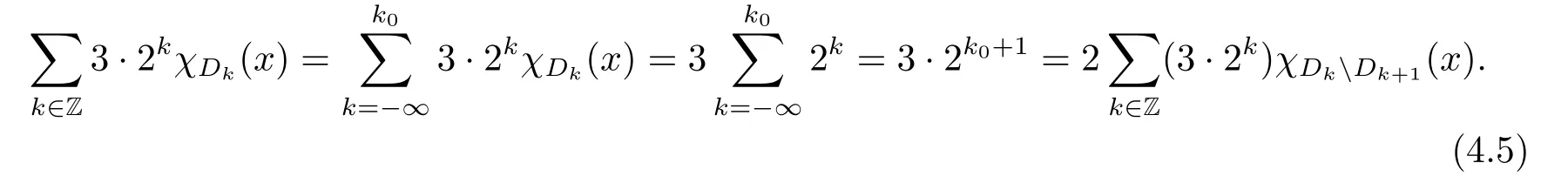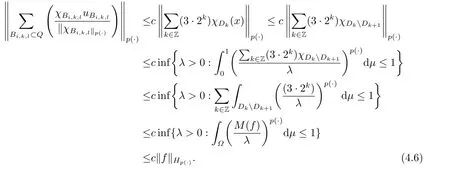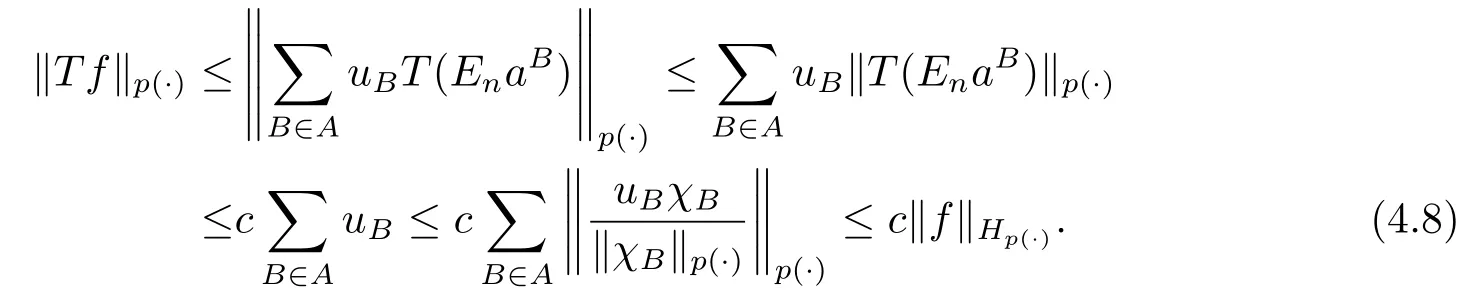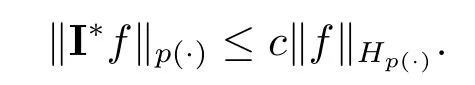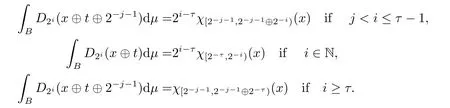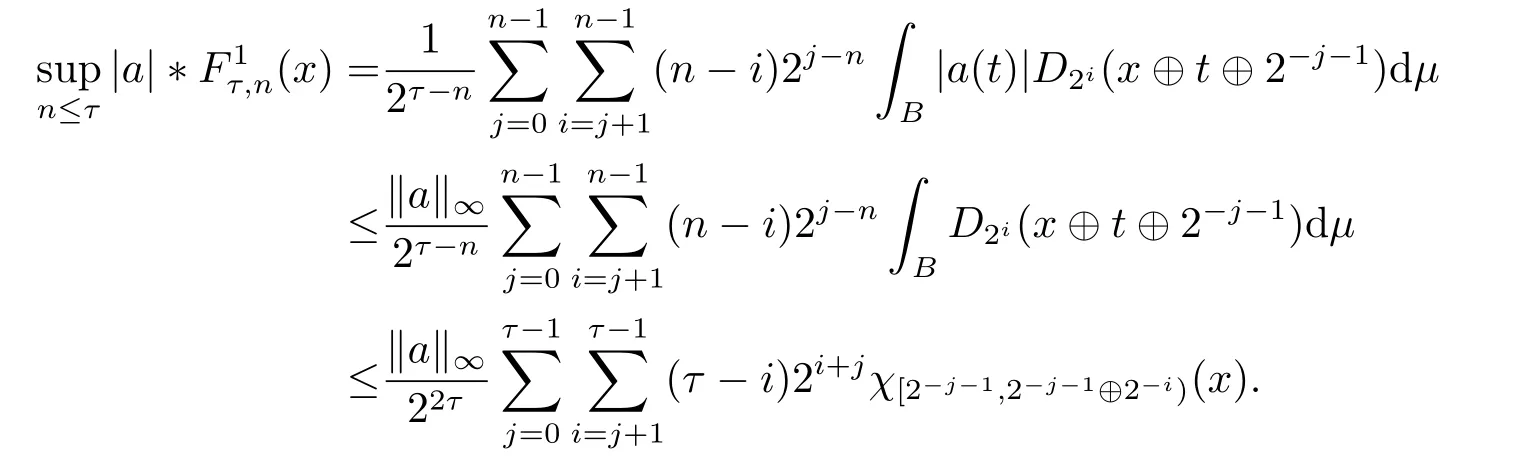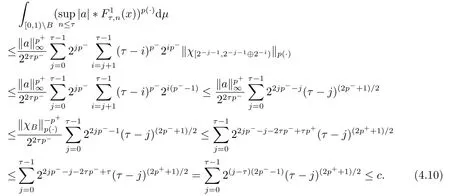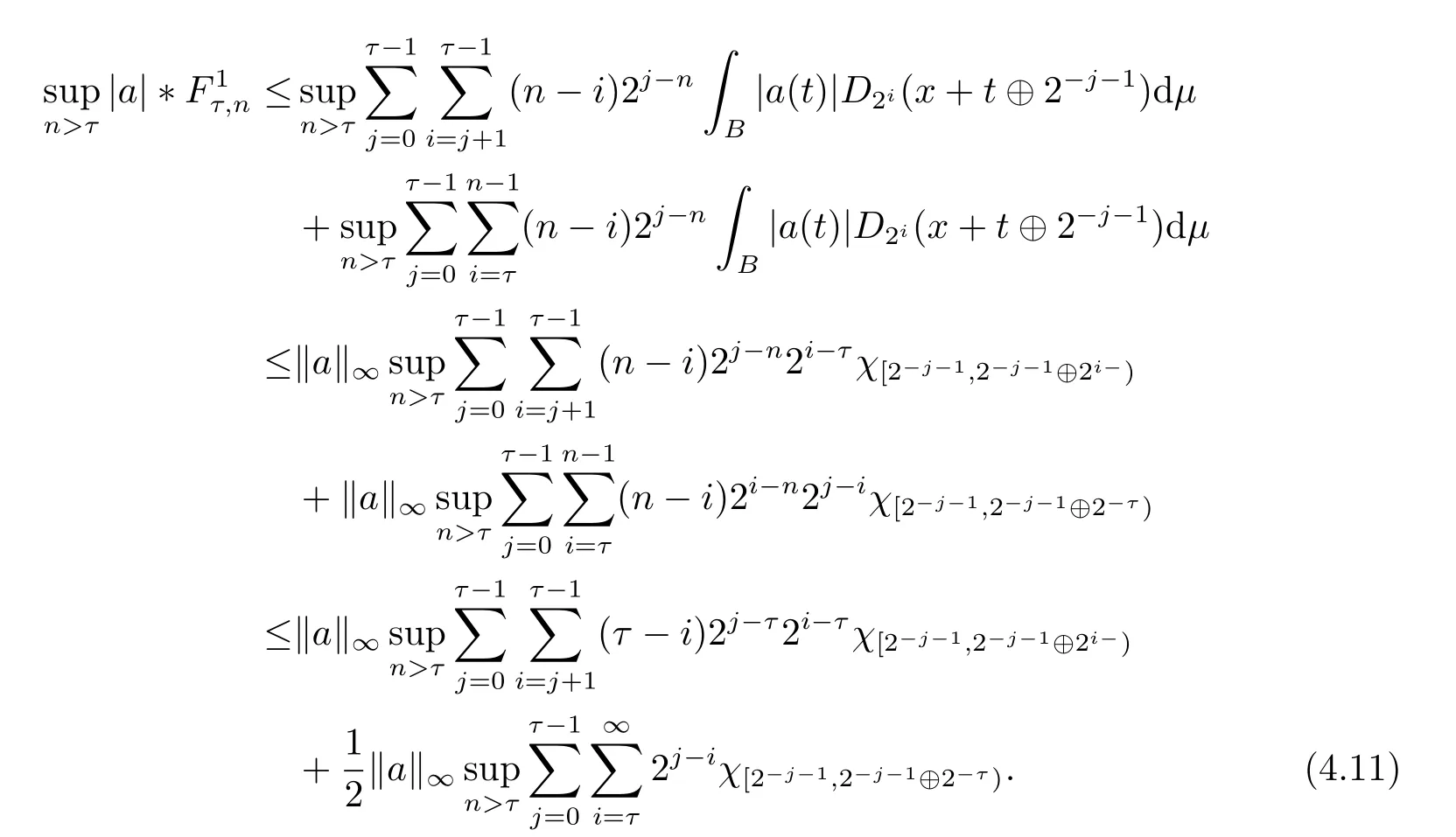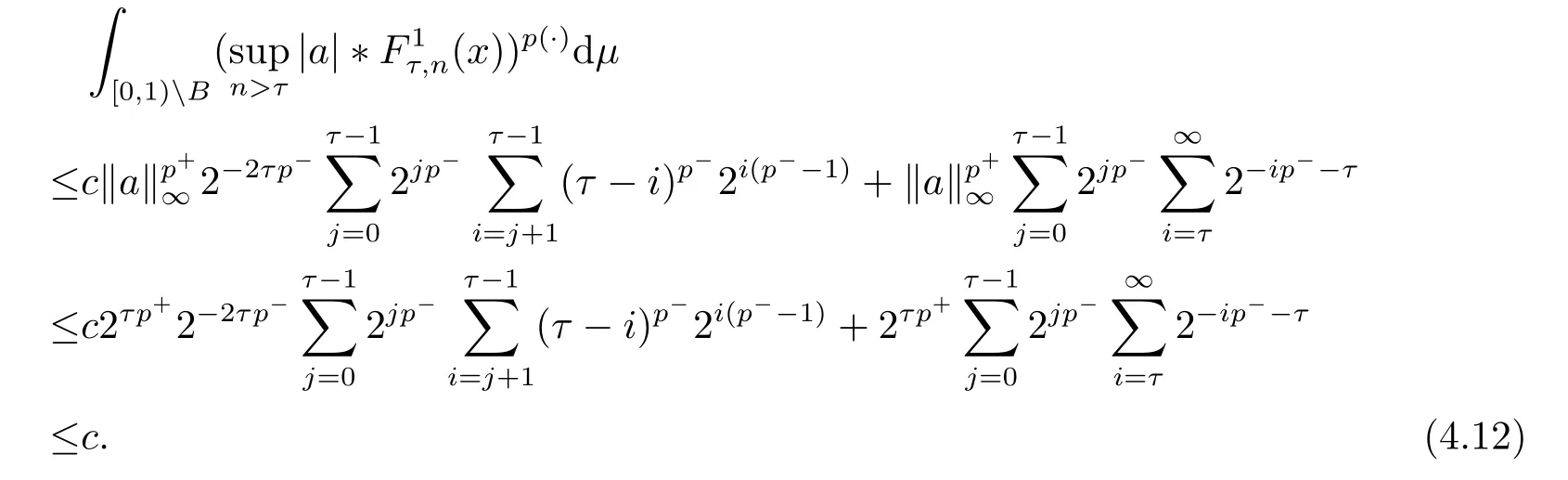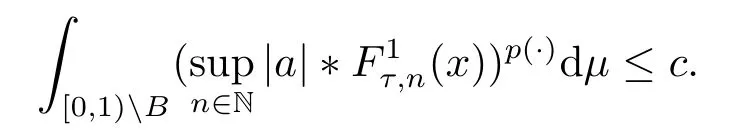The Boundedness of Maximal Dyadic Derivative Operator on Dyadic Martingale Hardy Space with Variable Exponents
ZHANG Chuanzhou(張傳洲),XIA Qi(夏綺),ZHANG Xueying(張學(xué)英)
(College of Science,Wuhan University of Science and Technology,Wuhan 430065,China)
Abstract: In this paper,we research dyadic martingale Hardy space with variable exponents.By the characterization of log-H?lder continuity,the Doob’s inequality is derived.Moreover,we prove the boundedness of maximal dyadic derivative operator by the atomic decomposition of variable exponent martingale space,which generalizes the conclusion in classical case.
Key words: Martingale;Variable exponent;Dyadic derivative;Atomic decomposition
1.Introduction
It’s well known that Musielak-Orlicz spaces and their special case,variable exponent Lebesgue spaces have been got more and more attention in modern analysis and functional space theory.In particular,Musielak-Orlicz spaces were studied by Musielak[11].Hudzik and Kowalewski[8]studied some geometry properties of Musielak-Orlicz spaces.Kovacik and Rakosnik[9],FAN and ZHAO[6]investigated various properties of variable exponent Lebesgue spaces and Sobolev spaces.Diening[5]and Cruz-Uribe[2?4]proved the boundedness of Hardy-Littlewood maximal operator on variable exponent Lebesgue function spacesLp(·)(Rn) under the conditions that the exponentp(·) satisfies so called log-H?lder continuity and decay restriction.Many other authors studied its applications to harmonic analysis and some other subjects.
The situation of martingale spaces is different from function spaces.For example,the good-λinequality method used in classical martingale theory can not be used in variable exponent case.Recently,variable exponent martingale spaces have been paid more attention too.Aoyama[1]proved that,ifp(·) isF0-measurable,then there exists a positive constantcsuch that‖M(f)‖Lp(·)≤c‖f‖Lp(·)forf∈Lp(·).Nakai and Sadasue[12]pointed out that the inverse is not true,namely,there exists a variable exponentp(·) such thatp(·) is notF0-measurable,and the above inequality holds,under the assumption that everyσ-algebraFnis generated by countable atoms.HAO[7]established an atomic decomposition of a predictable martingale Hardy space with variable exponents defined on probability spaces.Motivated by them,we research dyadic martingale Hardy space with variable exponents.Firstly,we give the characterization of log-H?lder continuity.By this,the Doob’s inequality is derived.Secondly,we give the atomic decomposition of variable exponent martingale space.Moreover,we prove the boundedness of maximal dyadic derivative operator.
2.Preliminaries and Notation
In this paper the unit interval [0,1) and Lebesgue measureμare to be considered.Through this paper,denote Z,N the integer set and nonnegative integer set,respectivety.By a dyadic interval we mean one of the form[k2?n,(k+1)2?n):=Iknfor somek∈N,0≤k <2n.Givenn∈N andx∈[0,1),letIn(x) denote the dyadic interval of length 2?nwhich containsx.Theσ-algebra generated by the dyadic intervals{In(x):x∈[0,1)}will be denoted byFn,more precisely,
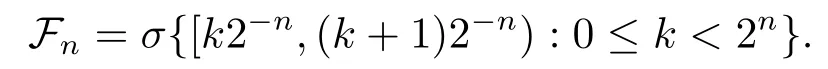
Obviously,(Fn) is regular.DefineF=σ(∪nFn) and denote the set of dyadic intervals{[k2?n,(k+ 1)2?n),0≤k <2n} byA(Fn) and writeA=∪nA(Fn).The conditional expectation operators relative toFnare denoted byEn.For a complex valued martingalef=(fn)n≥0,denotedfi=fi?fi?1(with conventiondf?1=0) and
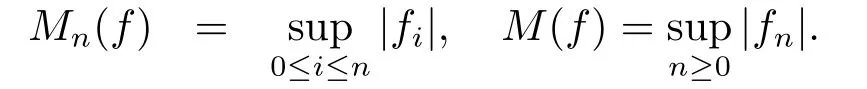
It is easy to see that,in casef∈L1[0,1),the maximal function can also be given by
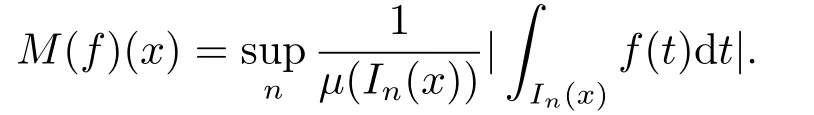
Proposition 2.1[10]If (Fn) is regular,then for all nonnegative adapted processesγ=(γn) andλ≥‖γ0‖∞,there exist a constantc>0 and a stopping timeτλsuch that

Lettingp(·):[0,1)→(0,∞) be anF-measurable function,we define

We use the abbreviationsp+=andMoreover whenp(·)≥1,we also define the conjugate functionp′(·) byLetP([0,1)) denote the collection of allF-measurable functionsp(·):[0,1)→(0,∞) such that 0 We say thatpis log-H?lder continuous if whend(x,y)≤1/2. The Lebesgue space with variable exponentp(·) denoted byLp(·)is defined as the set of allF-measurable functionsfsatisfying where Then we define the variable exponent martingale Hardy space analogous to classical martingale Hardy space as follows We always denote bycsome positive constant,it may be different in each appearance. Lemma 3.1Assume thatp+<∞,the following two conditions are equivalent: (i)pis log-H?lder continuous; (ii) For allt∈[0,1) andn∈N,we have Proof(i)?(ii) Sincex,y∈In(t),thend(x,y)≤2?n.Thus Moreover,we have (ii)?(i) Letx,y∈[0,1) be points withd(x,y)≤1/2,i.e.y∈I1(x) ory∈I1(x+1/2)which implyy∈I0(x).Thus we have sopis log-H?lder continuous. Remark 3.1[8]Ifpis log-H?lder continuous,then we have Lemma 3.2Suppose thatpis log-Hlder continuous with 1 ProofFixx∈[0,1) and letInbe a dyadic interval which containsx.By Theorem 2.8 in [9],we haveUsing H?lder’s inequality for the fixed exponentwe find that Then for everyx∈[0,1) we have Theorem 3.1Suppose thatpis log-H?lder continuous with 1 ProofWe assume that‖f‖p(·)≤1/2 by homogeneity.Sincewe have First we introduce the Walsh system.Every pointx∈[0,1) can be written in the following way: In case there are two different forms,we choose the one for which Forx,y∈[0,1) we define which is also called dyadic distance. The functions are called Rademacher functions. The product system generated by these functions is the Walsh system: wheren=andnk∈N. Recall that the Walsh-Dirichlet kernels satisfy Moreover,for any measurable functionf,the sequence{f ?D2n:=fn} is a martingale sequence. The Walsh-Fejér kernels are defined with and can be estimated by wherex∈[0,1),n,N∈N,2N?1≤n<2N. Butzer and Wagner[13]introduced the concept of the dyadic derivative as follows.For each functionfdefined on [0,1),set Thenfis said to be dyadically differentiable atx∈[0,1) if (dnf)(x) converges asn→∞.It is verified that every Walsh function is dyadically differentiable andfor allx∈[0,1) andk∈N.LetWbe the function whose Walsh-Fourier coefficients satisfy Set and let us estimate|dnWK|. Lemma 4.1[14]We have for alln,K∈N, where The dyadic integral off∈L1is introduced by Notice thatW∈L2?L1,so I is well-defined onL1. We consider the maximal dyadic derivative operator Definition 4.1A pair (a,B) of measurable functionaandB∈A(Fn) is called ap(·)-atom if 1)En(a)=0, 3){a≠0}?B. Theorem 4.1Suppose thatpis log-Hlder continuous and 1/2 and ProofWe apply Proposition 2.1 to the process (|fn|)n≥0andλ=2k,k∈Z.We obtain the stopping timeτksatisfyingτk≥τl,k≥l,limk→∞τk=∞a.e.,limk→∞fτkn=fna.e.and Consequently,fncan be written as Since{τk=l}∈Fl,we have a family ofBi,k,l∈A(Fl) such that WriteuBi,k,l=3·2k+1‖χBi,k,l‖p(·).WhenuBi,k,l≠0,define SinceM(fτkn)≤2k,k∈Z,the definition ofuBi,k,lyields ThusaBi,k,l=()n≥0is aL2-bounded martingale.Consequently,there exists aaBi,k,l∈L2such thatEn(aBi,k,l)=aBi,k,ln.Sinceτk+1>τk=l,we have Therefore (aBi,k,l,Bi,k,l) is really ap(·)-atom. For anyk∈Z,defineDk={τk <∞}.Sinceτkis non-decreasing for eachk∈Z,we haveDk ?Dk+1.For any givenx∈[0,1),there isk0∈Z such thatx∈Dk0Dk0+1.Then Therefore,for anyQ∈Awe have Thus we complete the proof. Theorem 4.2Suppose that the operatorTis sublinear and for eachp0 for everyp(·)-atom (a,B).IfTis bounded fromL∞toL∞,then ProofSupposing (a,B) is ap(·)-atom andL∞boundedness ofT,we obtain Thus for everyf∈Hp(·),we have Theorem 4.3Suppose thatpis log-Hlder continuous and 1/2 ProofBy Theorem 4.2,the proof of Theorem 4.3 will be completed if we show that the operatorI?satisfies (4.7) and is bounded fromL∞toL∞.Obviously, and Since‖D2n‖1=1,we can show that‖F(xiàn)i0,n‖1≤cfori=1,2,···5.From this it follows that‖dnW‖1≤cfor alln∈N,which verifies that I* is bounded onL∞. Ifa ≡1,then the left hand side of(4.9)is zero.Leta≠1 be an arbitraryp(·)-atom with supportBandμ(B)=2?τ.Without loss of generality,we may suppose thatB=[0,2?τ). Fork <2τ,ωkis constant onBand so Moreover To verify (4.7) we have to investigate the integral of (supn|a|?Fiτ,n(x))p(·)over [0,1)Bfor alli=1,2,···,5.Sincex∈[0,1)B,we have By the definition of an atom, Integrating over [0,1)B,we obtain Letn>τ.Ifj >τandx /∈B,thenx ⊕2?j?1/∈B.Consequently,forx /∈B,i≥j >τwe have Thus We can see as above that By (4.11) and (4.12) we have Similarly,we can also estimate the integral (supn|a|?Fiτ,n(x))p(·)over [0,1)Bfor alli=2,···,5.We omit it.By Theorem 4.2,we complete the proof. Corollary 4.1Suppose thatpis log-H?lder continuous and 1/2



3.Doob’s Inequality on Dyadic Martingale Space

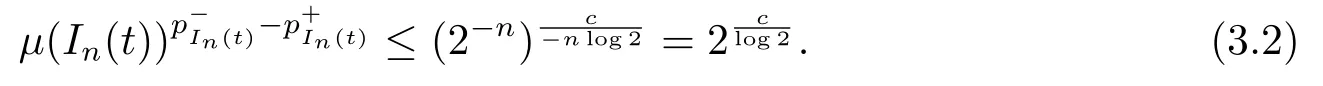





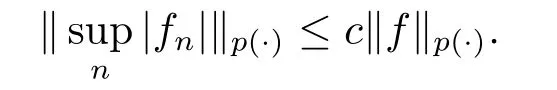
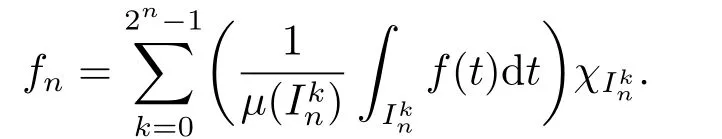
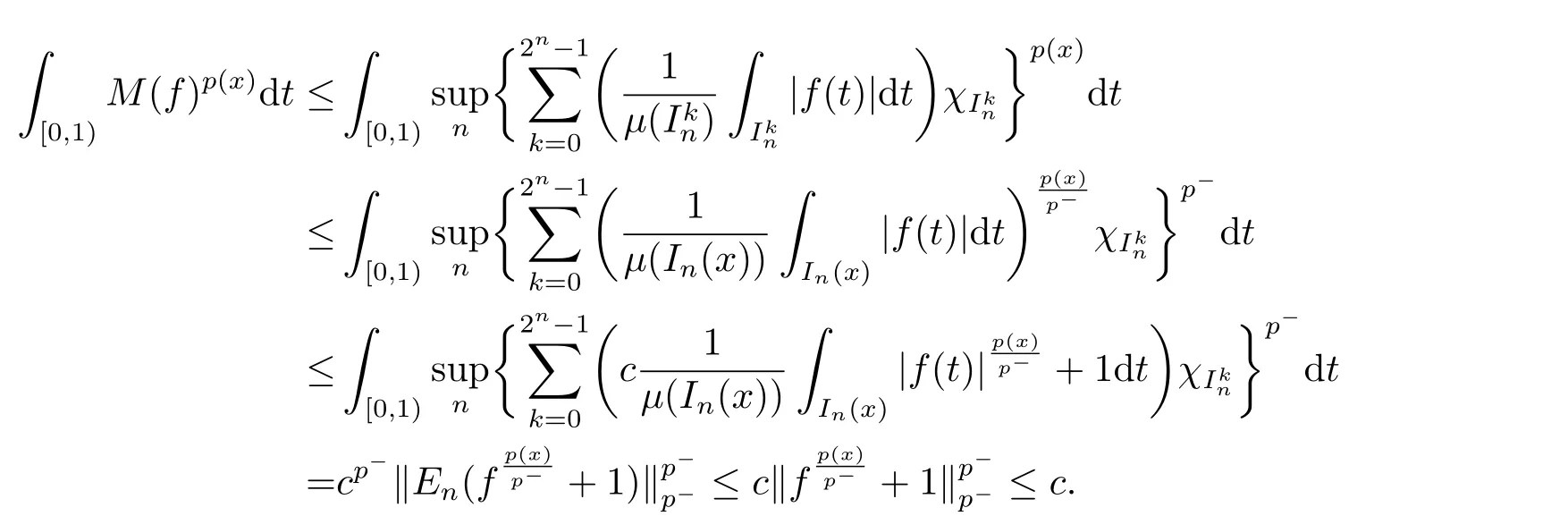
4.Dyadic Derivative