求二次比式和問題全局解的一個新的確定性算法

張博,高岳林

(1.北方民族大學數學與信息科學學院,寧夏 銀川750021;2.寧夏科學計算與智能信息處理協同創新中心,寧夏 銀川750021)

1.引言

分式規劃問題是非線性全局優化的一個重要分支,而二次比式和規劃問題是又一類特殊的分式規劃問題.在現實生活中,許多實際問題均可抽象為二次比式和規劃模型,且在投資問題、運輸方案、經濟效益、生產管理等領域有著廣泛的應用背景.數十年來它吸引了許多專家和學者的高度關注;其次,從研究的觀點來看,二次比式和規劃問題對理論分析和計算求解的方式提出了挑戰.本文主要考慮以下形式的二次比式和規劃問題(QFP):

這里,p≥2,H1i(x),H2i(x)均為二次函數其表達式如下：

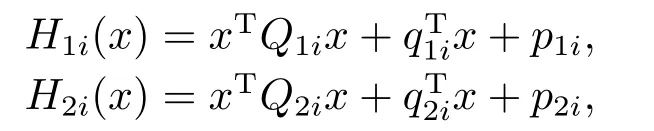
其中,b∈Rn,A∈Rm×n,Qsi∈Rn×n,qsi∈Rn,psi∈R,s=1,2,X是非空有界閉集.根據H2i(x)的連續性以及介值定理可知,對任意的x∈X有H2i(x)>0或者H2i(x)<0.如果存在某一個i∈{1,2,···,p}使得H2i(x)<0,用替代使得所有分式項的分母項均大于零;為了方便起見,假設此時,H1i(x)<0,H2i(x)>0,用替代其中M是一個充分大的正數,滿足對所有的x∈X,H1i(x)+MH2i(x)≥0,問題(QFP)的本質不變.因此,這里不失一般性,假定對所有的i=1,2,···,p,均有H1i(x)≥0,H2i(x)>0.

此外,對于問題(QFP)可能擁有多個局部最優解,這樣會干擾尋找全局最優解,使問題的難度增加,因此研究此類問題是必要的.本文為上述比式和規劃問題建立了一個分支定界算法.首先,通過線性代數矩陣滿秩分解的知識將原問題中通項的分子和分母的二次函數分別轉化為相應的兩項乘積和的形式,然后利用求解兩項線性乘積和規劃的知識[1]并結合一些線性化技巧分別構造問題目標函數中通項的下界,并基于此技巧構造出能夠為原問題提供可靠下界……