基于BQGA-ELM網絡在滾動軸承故障診斷中的應用研究

皮 駿， 馬 圣， 杜旭博， 賀嘉誠， 劉光才

(1.中國民航大學 通用航空學院，天津 300300；2.中國民航大學 航空工程學院，天津 300300)

在實際工程中，無論地面機械設施還是航空航天工業中所涉及的轉子機械，在長期的使用過程中會出現機械故障，尤其是轉子機械的軸承故障。如：航空發動機四號軸承，由于它所處的位置特殊，因此對它進行監控診斷難度較大。為了更好的解決這些問題，需要對故障診斷方法進行研究[1-2]。旋轉機械中的軸承性能狀態，將直接影響到機械設施能否正常有效的工作[3]。但由于軸承壽命離散度較大，因而廣泛引起國內外諸多學者的重視。

隨著對轉子動力學[4]的深入研究，根據物體的振動信號亦能診斷故障。這種方法避免了人為因素的干擾，但對振動信號的準確提取提出嚴苛的要求[5-6]。在信號采集、處理等過程中，故障振動信息的部分特征可能會丟失，這就造成了信號的模糊性。由于部分智能算法具有模糊識別的能力，即使故障振動信號的提取不是絕對準確，也能得到較好的診斷結果。因此在文獻[7-10]中，學者利用不同的信號處理手段對軸承故障振動信號進行處理，并分別結合支持向量機[11]、多核學習機[12]、人工神經網絡[13-14]、Elman[15]網絡和RBF[16]網絡對軸承故障進行診斷，并取得較好的成果。雖然這些學者運用部分神經網絡在診斷中得到較好的結果，但由于部分神經網絡收斂速度較慢、易陷于局部最優，因而得到的結果仍有提升的空間。

針對部分前饋型神經網絡存在的缺陷問題，Huang等[17]人提出了極限學習機神經網絡(Extreme Learning Machine,ELM)的概念。ELM避免了傳統前饋神經網絡對學習速率、終止條件、易陷于局部極優等缺陷，因而廣泛用于數據壓縮、特征學習、聚類、診斷等領域。近年來，ELM網絡被運用到航空發動機、機械等諸多領域的故障診斷中，同時得到了比部分前饋神經網絡更好的診斷結果。雖然ELM網絡的優勢明顯，但它相比傳統神經網絡可能需要更多的隱含層神經元數量，且隨機賦予輸入權值和閾值，可能會導致病態問題出現[18]。因此，部分學者提出用智能優化算法對網絡進行優化，如：盧錦玲等[19]利用改進粒子群算法和交叉驗證優化極限學習機，并將優化的學習機用于軸承故障診斷；徐繼亞等[20]利用鯨魚算法優化極限學習機，并用于軸承故障診斷；Yang等[21]利用量子粒子群算法優化極限學習機，并對航空發動機故障進行診斷；Lu等[22]引入傳感器故障失效率改進ELM網絡，并用于傳感器的故障診斷與重構。但GA(Genetic Algorithm)和PSO(Particle Swarm Optimization)等優化算法均存在一些缺陷[23]，所以用來PSO和GA優化ELM網絡不能得到很好的效果。針對ELM網絡缺陷和軸承故障診斷問題，本文提出Bloch球面量子遺傳算法優化極限學習機網絡作為滾動軸承故障診模型。

量子遺傳算法[24]是在傳統的GA中引入量子并行計算，極大地加快了算法對信息的處理速度。與傳統的GA不同的是，量子遺傳算法(Quantum Genetic Algorithm，QGA)用量子比特取代傳統遺傳算法中的二進制染色體；QGA采用量子門操作更新種群，能夠對空間進行有效搜索；同時采用量子位的平面坐標進行染色體編碼，使得染色體數量為單一編碼的二倍，因而增加種群的多樣性。但量子遺傳算法也存在部分缺陷，如：頻繁的二進制解碼、量子旋轉方向基于查表等。針對QGA存在的這些問題，Pan[25]提出的Bloch球面量子遺傳算法(Bloch QGA, BQGA)，BQGA比QGA擁有更好的多樣性和收斂性特征，且具有良好的空間搜索能力。在Bloch球面量子遺傳算法中，通過相位翻轉實現量子染色體的變異，從而能夠有效地保持種群的多樣性。因此，本文使用Bloch球面量子遺傳算法優化極限學習機網絡的輸入權值和隱含層閾值，再用Moore-Penrose算法計算ELM網絡的輸出權值矩陣，最后使用優化的ELM網絡對滾動軸承故障進行診斷。

1 極限學習機相關理論模型

Huang等提出極限學習機網絡，ELM網絡隨機賦予輸入權值和閾值，便能逼近任意非線性分段函數[26]。設ELM網絡輸入層有n個神經元，隱含層有l個神經元，輸出層有m個神經元，則ELM網絡的輸入權值矩陣表示為

(1)

式中：ωij為輸入層第i個神經元與隱含層第j個神經元間的連接權值。記隱含層與輸出層之間的連接權值矩陣為

(2)

式中：βjk為隱含層第j個神經元與輸出層第k個神經元間的連接權值。設隱含層神經元的閾值矩陣為

(3)

若存在Q個有效樣本，其輸入矩陣X和輸出矩陣T分別為

(4)

若ELM網絡隱含層神經元激活函數為g(x)，則Q個有效樣本輸出矩陣T中的任意元素tmQ可由式(5)計算

(5)

因此，輸出矩陣T的計算可簡記為

Hβ=T′

(6)

式中：H為ELM網絡隱含層輸出矩陣；T′為ELM網絡輸出矩陣T的轉置；β為ELM網絡輸出權值。輸出權值β可由最小二乘法求得

(7)

式中：H+為輸出矩陣H的Moore-Penrose廣義逆。由于最小二乘法能求得唯一解，因此ELM網絡使用Moore-Penrose廣義逆能夠極大的提高學習效率。

文中所用到的隱含層激活函數為

(1)Sigmoid()函數

(2)Sin()函數

f(a,b,x)=sin(ax+b)

(3)RBF()函數

f(a,b,x)=e(-b‖x-a‖2)

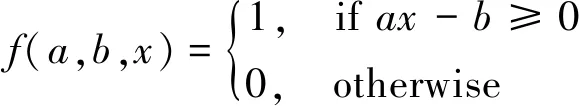
2 基于Bloch球面量子遺傳算法優化的ELM網絡(BQGA-ELM)

2.1 優化過程描述

極限學習機網絡相比傳統神經網絡可能需要更多的隱含層神經元，且由于隨機賦予輸入權值和閾值，可能會導致病態問題出現。因此，針對這一問題，本文提出使用Bloch球面量子遺傳算法優化ELM網絡，并應用于滾動軸承故障診斷之中。則BQGA優化ELM網絡的流程圖如圖1所示。

BQGA-ELM的具體步驟如下：

步驟1設置相關參數，包括種群大小、迭代步數、相位旋轉步長等；

步驟2Bloch球面上的某一點P，給定相位角θ和φ便可表示為|φ〉=[cosφsinθsinφsinθcosθ]T。因此，用量子位在Bloch球面上的坐標對染色體進行編碼，即

(8)

在式(8)的編碼方式中，φij=2π×rand；θij=π×rand；rand為(0,1)之間的隨機數；i=1,2,…，sizepop，j=1,2,…,n，sizepop表示種群規模，n表示量子位數(即：待優化的變量個數)。BQGA中，每條量子染色體包含三條并列基因鏈， 即量子位的xyz坐標， 而每條基因鏈表示待優化變量的一組近似解；

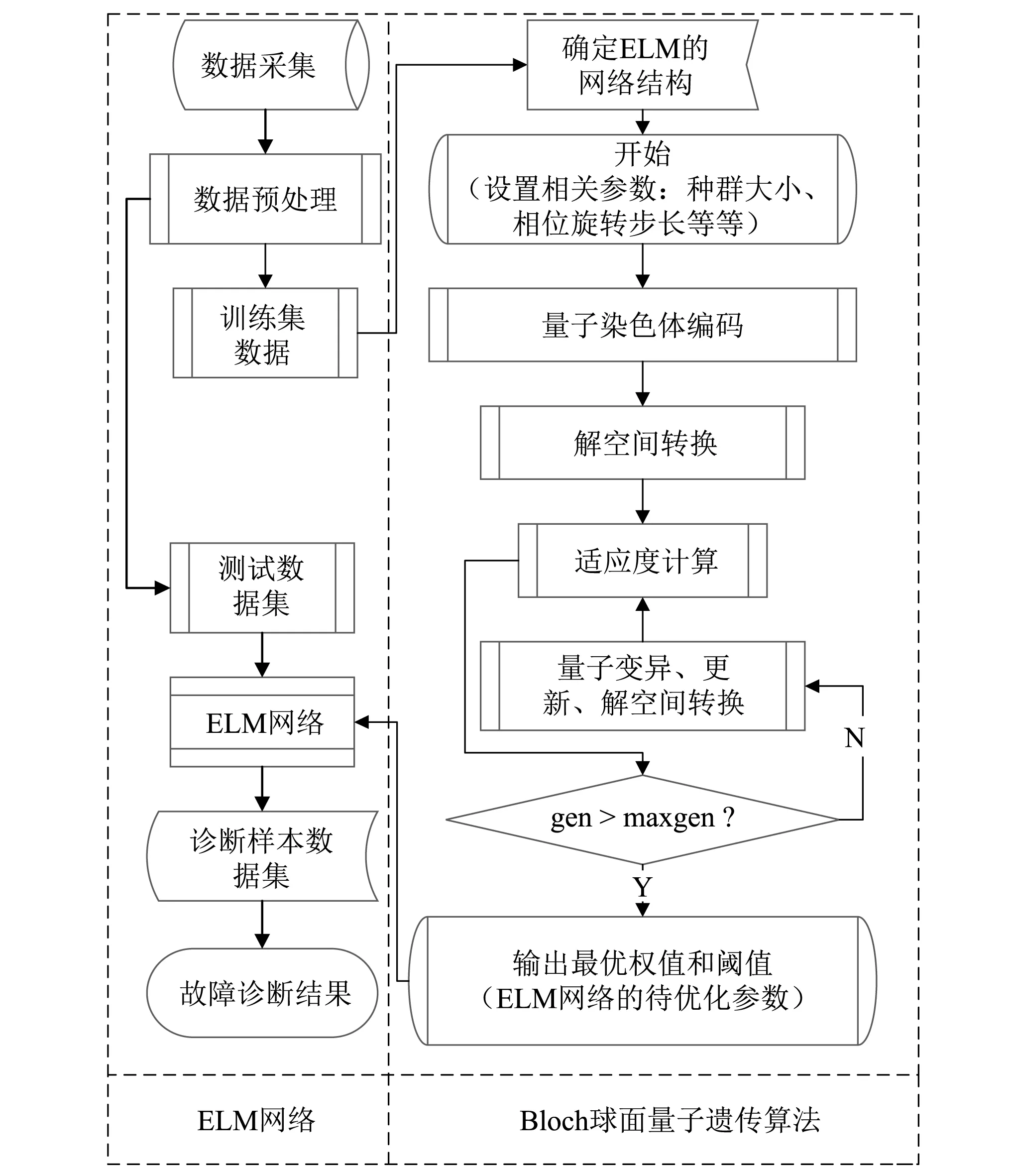
圖1 BQGA-ELM算法流程圖Fig.1 Flowchart of BQGA-ELM algorithm

步驟3將三組近似解進行解空間轉換，即將近似解轉換到目標函數的解空間；

步驟4根據式(9)的適應度函數，計算近似解的適應值。找出當前最優適應值與對應的當前最優染色體，同時將當前最優解轉存為全局最優解；

①見“UN should play a more effective role”.Beijing Review,1 November 1982:11-12．

(9)

式中：n為校驗集樣本數量；yi為網絡期望輸出；oi為真實輸出。

步驟5利用量子旋轉門U，更新量子染色體，得到新的量子染色體，即式(10)

(10)

式中：Δφ和Δθ為相位旋轉步長。

步驟6對旋轉更新后的新染色體進行解空間轉換，并計算新染色的適應度值，保存當前最優解與對應的染色體；

步驟7比較當前最優解和全局最優解。如果當前最優解優于全局最優解，則全局最優解被替換；否則繼續；

步驟8判斷是否滿足終止條件。若是，則輸出最優解；若否，則繼續循環執行步驟5～步驟7。

2.2 算法仿真校驗

為了驗證BQGA在ELM網絡優化中的可行性，選取UCI標準數據庫中的Wine和Abolone兩個標準數據集作為實驗數據，仿真數據集的相關屬性及數據集分配如表1所示。對比研究Bloch球面量子遺傳算法優化ELM網絡(BQGA-ELM)、量子遺傳算法優化ELM網絡(QGA-ELM)、粒子群算法優化ELM網絡(PSO-ELM)、經典遺傳算法優化ELM網絡(GA-ELM)以及未被優化ELM網絡六種方法之間的性能，此六種方法文中簡稱為診斷模型。ELM網絡的四種激活函數(Sigmoid()、Hardlim()、Sin()、RBF())均被考慮其中，計算結果中主要呈現測試集診斷準確率、均方根誤差、神經元數量以及計算耗時。

比較研究采用的計算機配置為:AMDA8-5500B APU with Radeon HD Graphics四核處理，金士頓DDR3L 4 G 800 MHz內存，文中所有算法均在MATLAB2014a上運行。

對比算法的參數設置說明：遺傳算法共有參數設置如下，種群大小為20，迭代步數100，種群范圍為[-0.5 0.5]；傳統遺傳算法交叉概率為0.6，變異概率為0.05；經典粒子群算法中，種群粒子數為20，迭代步數為100，粒子最大速度為0.1，最小速度為-0.1，粒子范圍為[-0.5 0.5]；量子遺傳算法中的變異概率為0.05；相位旋轉角均為：0.01π；ELM網絡中神經元數量設置見表。計算結果統計如表2和表3所示。

表1 仿真數據樣本集信息

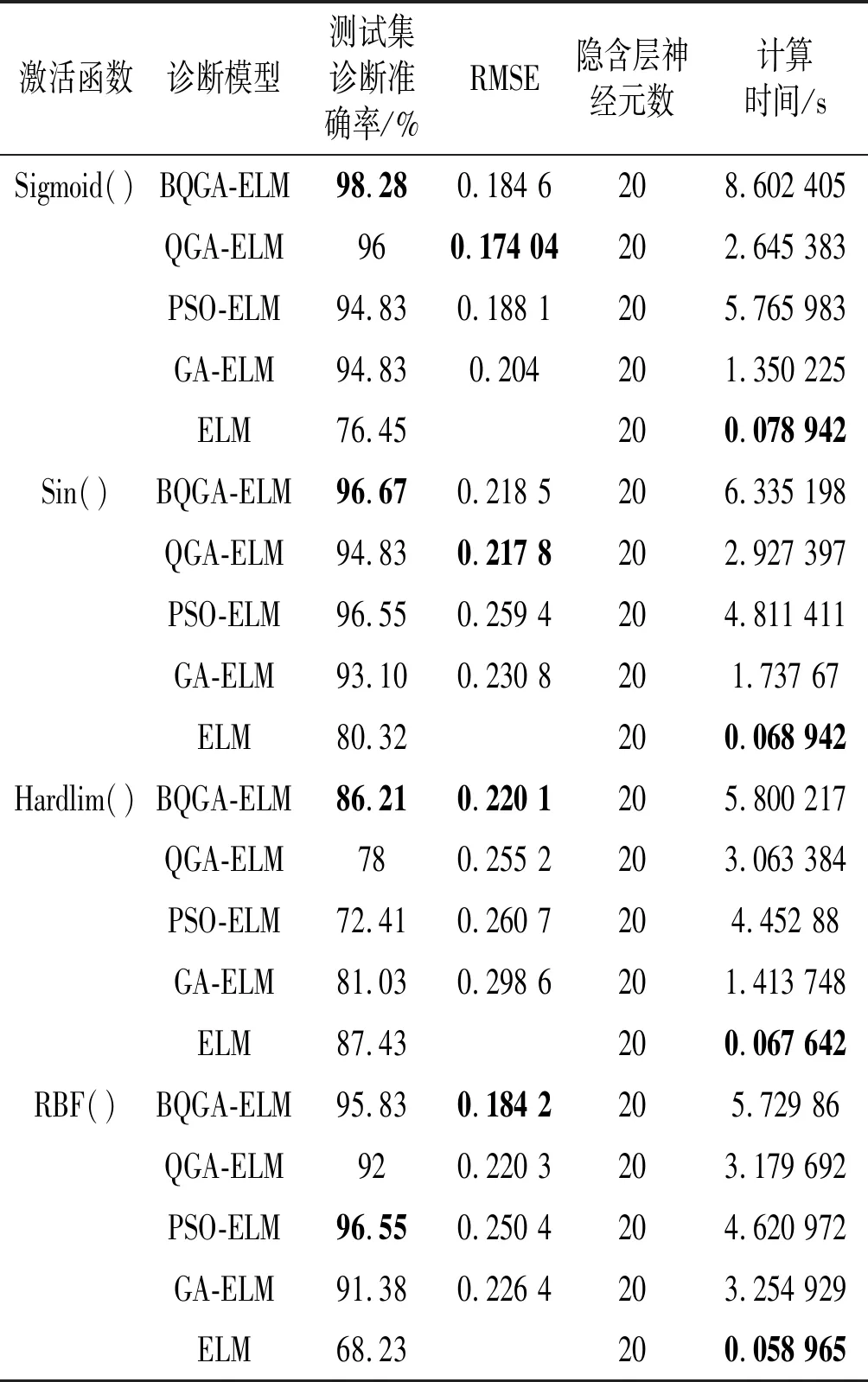
表2 樣本集Wine的診斷結果

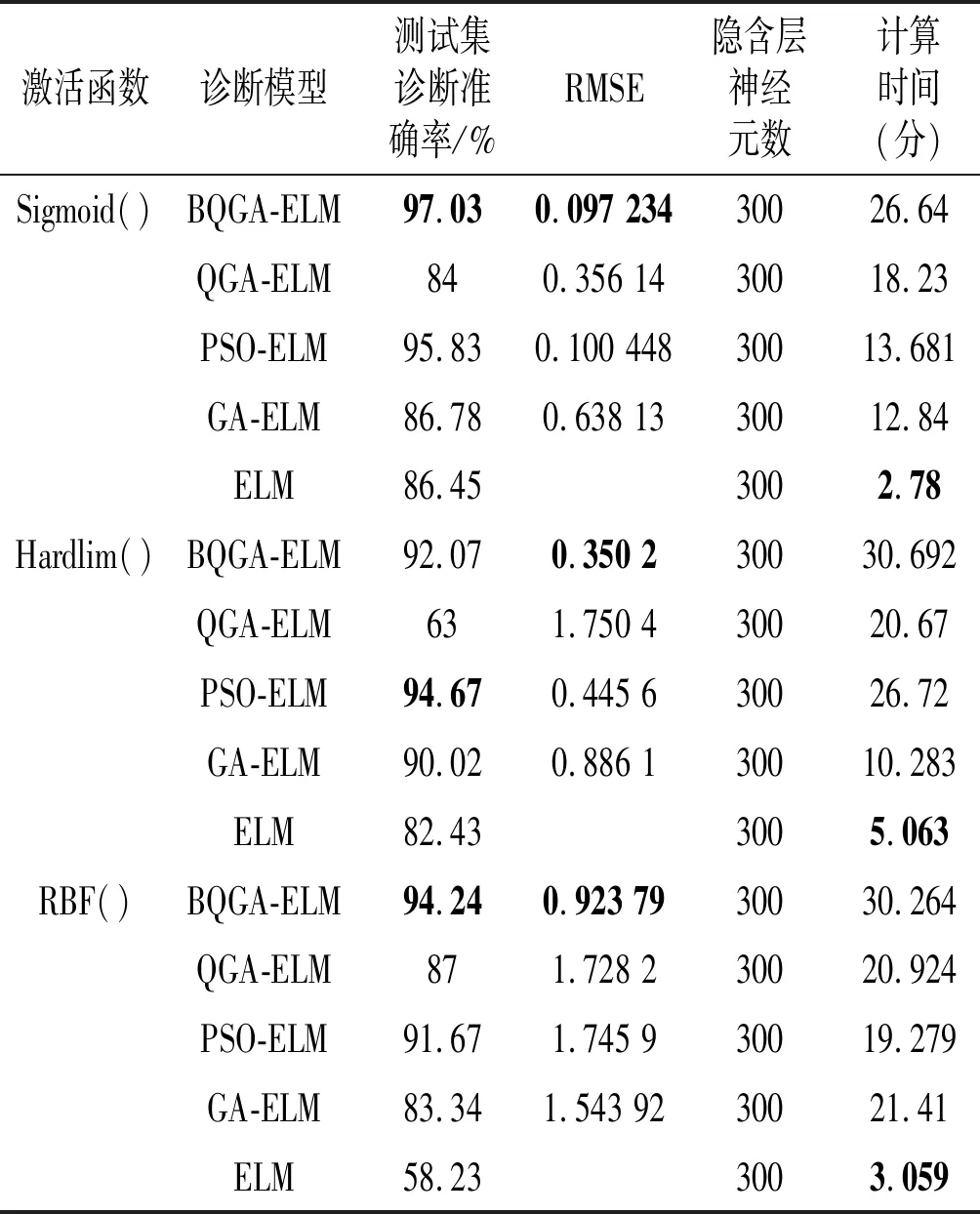
表3 樣本集Abolone的診斷結果

表2和表3呈現不同方法優化ELM網絡后的計算結果，計算結果均為30次分類實驗后的平均值，計算得到的最優結果在表2和表3中已用黑體加粗進行標記。在不同激活函數下，診斷效果差異較為明顯，因此使用ELM網絡時，應適當選擇激活函數。從表2和表3中的加粗黑體可以發現，BQGA-ELM模型的診斷效果最好，PSO-ELM模型其次，ELM網絡最差；這一結果表明BQGA在空間尋優的能力由于其它方法，但隨著其搜索維度的增加，計算量增大，其計算時間也相應增加；同時也凸顯出優化的ELM克服了ELM網絡中的部分缺陷。需要注意的是，ELM網絡隱含層神經元數對分類結果有影響，由于仿真測試小節并非本文的重點，所以此處并未對神經元數量進行分析，只是為了驗證文中診斷模型的可行性。

3 滾動軸承故障數據采集實驗

3.1 軸承故障實驗簡介

由于航空發動機軸承故障數據采集難度較大、成本較高，因此故障數據通過實驗模擬的方式獲得。滾動軸承故障診斷實驗裝置如圖2所示。

圖2 滾動軸承實驗裝置Fig.2 The test rig of the rolling element bearing

其中，實驗中所用設備包括：307型滾動軸承、加速傳感器、光電傳感器、電荷、信號調理機、計算機等。軸承座可以拆卸， 便于更換不同故障類型的軸承。聯軸器上貼有反光紙作為相位起始標志，光電傳感器提供轉速和鍵相信號；置于故障軸承軸向、徑向垂直和徑向水平方向的加速度傳感器測得軸承振動信號；最后再經過電荷放大器送至設備CAMD-6100型信號調理器處理。

實驗中轉子轉速為988 r/min，每周期傳感器采樣1 024個點，每次實驗采集16個周期。307型滾動軸承幾何參數如表4所示；實驗故障類型為：正常、內環故障、外環故障、滾珠故障，故障類型尺寸數據如表5所示，故障類型加工圖如圖3～圖5所示。

表4 307型滾動軸承的幾何參數

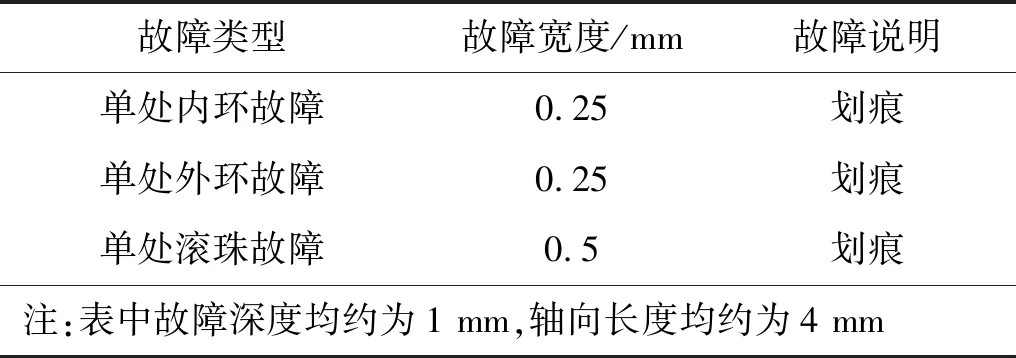
表5 滾動軸承模擬故障類型

圖3 滾動軸承內環單處劃痕故障示意圖Fig.3 The single scratch fault on the inner ring

圖4 滾動軸承外環單處劃痕故障示意圖Fig.4 The single scratch fault on the outer ring

圖5 滾動軸承滾珠單點點蝕故障示意圖Fig.5 The single erosion fault on a ball

3.2 軸承振動信號處理方式

在時域分析法中，特征參量峰值、峭度系數均為無量綱參數，且時域分析法處理過程不會使信號發生畸變或損失，采用最原始信息資料進行軸承故障診斷。首先，對采集到的軸承故障振動信號先進行時域分析；再利用SPSS軟件進行因子分析，根據碎石圖特征值遞減情形選擇累積方差貢獻率達到90%的因子，即：峰值、均值、均方根、方差、偏度、峭度；最后將這6個因子作為307型滾動軸承故障診斷的輸入特征量。

3.3 滾動軸承故障數據集樣本分配

將得到的數據集樣本分為：訓練集樣本、校驗集樣本、測試集樣本三部分，三部分數據隨機選擇，彼此互不重復。文中所用樣本分配如下：訓練集樣本容量為200個，校驗集樣本容量為100個，測試集樣本容量為100個。

4 滾動軸承故障診斷實例

4.1 數據標準化

為了避免故障特征量之間的數量級差異給診斷結果帶影響，因此按如式(11)進行歸一化處理

(11)

式中：xmax，xmin和xmean為某特征參量的最大值、最小值和平均值；xi是某特征參量的第i個值；x是歸一化后的值。

4.2 BQGA-ELM模型的輸出形式

極限學習機網絡采用三層結構，即：輸入層、隱含層和輸出層。輸入層神經元個數為：6個；隱含層神經元個數設置將影響到網絡診斷準確率，下小節將對隱含層神經元數量和激活函數進行分析；輸出層神經元個數設置為1，對于輸出神經元輸出結果的處理方式如表6所示。

表6 輸出結果的處理方式

4.3 隱含層神經元數量和激活函數的選擇

利用滾動軸承故障樣本數據，對幾種診斷模型進行分析，選擇合適的激活函數和神經元數量。在不同激活函數的前提條件下，分析神經元數量與測試集診斷準確率之間的關系，從而選擇合適的激活函數與神經元數量。其計算結果如圖6所示。

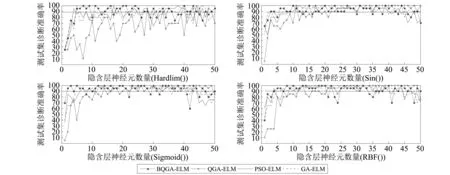
圖6 隱含層神經元數量和激活函數的選擇Fig.6 Choose of activation function and number of hidden neurons

從圖6中可以看出，幾種診斷模型在Hardlim()和RBF()函數下，測試集診斷準確率波動較為明顯；而在Sigmoid()和Sin()函數下，變化較為平緩，尤其在神經元數量處于[10,40]范圍內時，效果較好。直觀看來，診斷模型選擇Sigmoid()和Sin()函數時，對幾種算法而言效果均較好，且可比性較強；為了更加具有說服性，在每種激活函數下，統計各診斷模型測試準確率大于等于90%時出現的次數，并定義為頻數，根據診斷模型頻數的變化大小選擇激活函數。統計結果可視化為圖7所示。

從圖7中可以看出，當激活函數為Sigmoid()，Sin()和RBF()時，幾種診斷模型的頻率均相對較高。但仔細觀察發發現：在RBF()和Sin()函數下，幾種診斷模型之間的最大差異分別可達到15%和20%左右，不利于對比評估；而在Sigmoid()函數下，幾種診斷模型之間的差異最大可達到10%，相對較小。經過分析，選擇差異較小Sigmoid()函數作為幾種診斷模型的激活函數。因此，文中診斷模型的激活函數為Sigmoid()，神經元數量取值范圍為[10,40]。

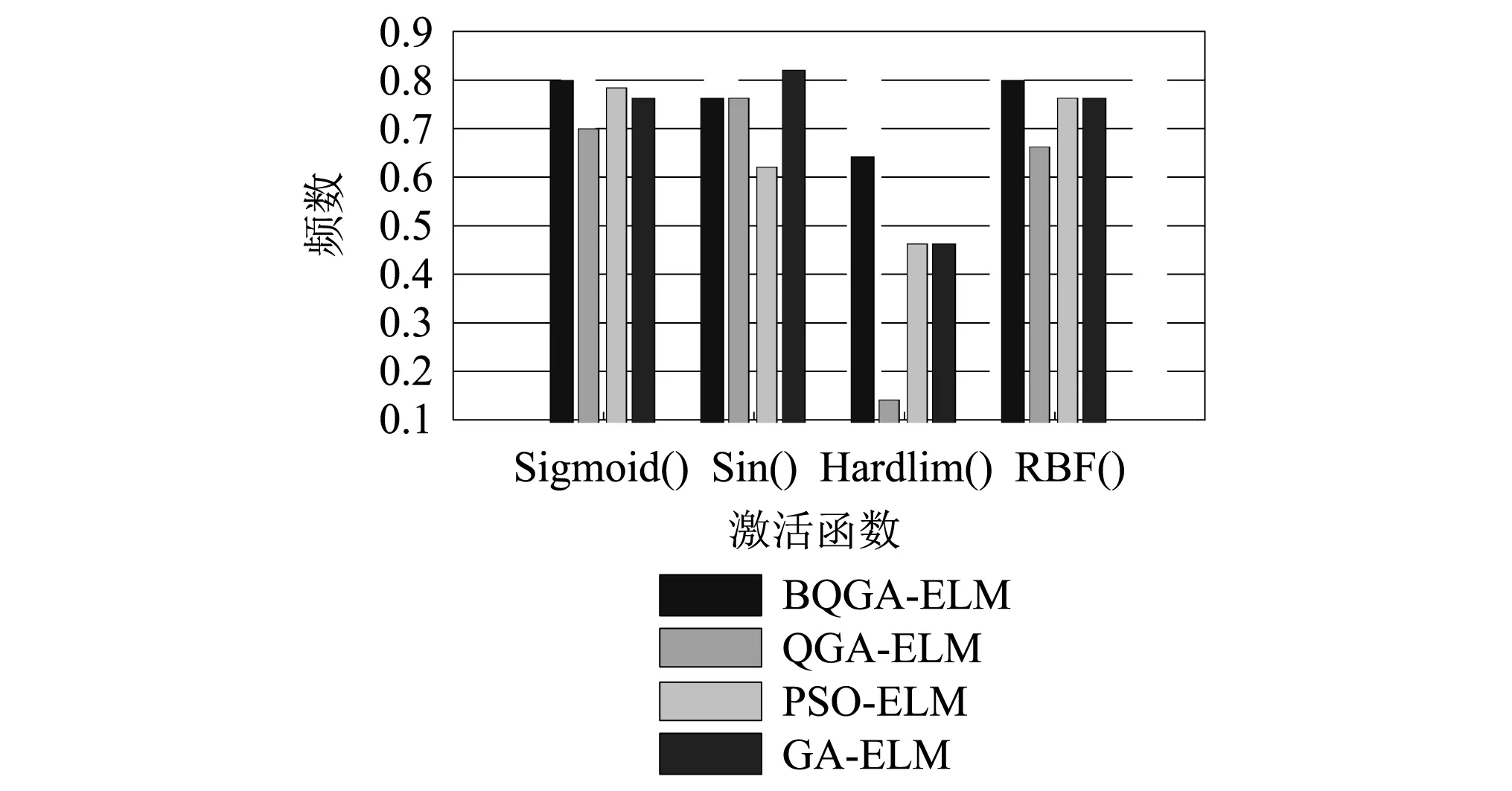
圖7 根據頻數選擇激活函數Fig.7 Choose of activation function according frequency

4.4 診斷結果評價標準

采用30次診斷后的平均值為文中評定的標準，平均診斷準確率按式(12)計算

(12)

式中：Accuracymean為平均準確率；T為重復診斷次數；y(t)為第t次診斷時，樣本診斷正確的個數；m為需要診斷的總樣本數量。

5 滾動軸承故障診斷結果分析

在本章節中，將從平均診斷準確率、誤差收斂情況以及診斷耗時三方面分析BQGA-ELM在滾動軸承故障診斷中的有效性。

5.1 平均診斷準確率

將在滾動軸承故障實驗章節中得到的四種軸承故障特征參量樣本，經過數據歸一化后，按照樣本分配方式進行隨機且不重復的分配。將分配好的訓練集樣本輸入診斷模型中進行訓練，用校驗集樣本對模型訓練效果進行校驗，選取最優權值閾值優化ELM網絡，并對測試集樣本進行診斷，其診斷結果如表7所示(最優結果已用黑體加粗標記而出)。

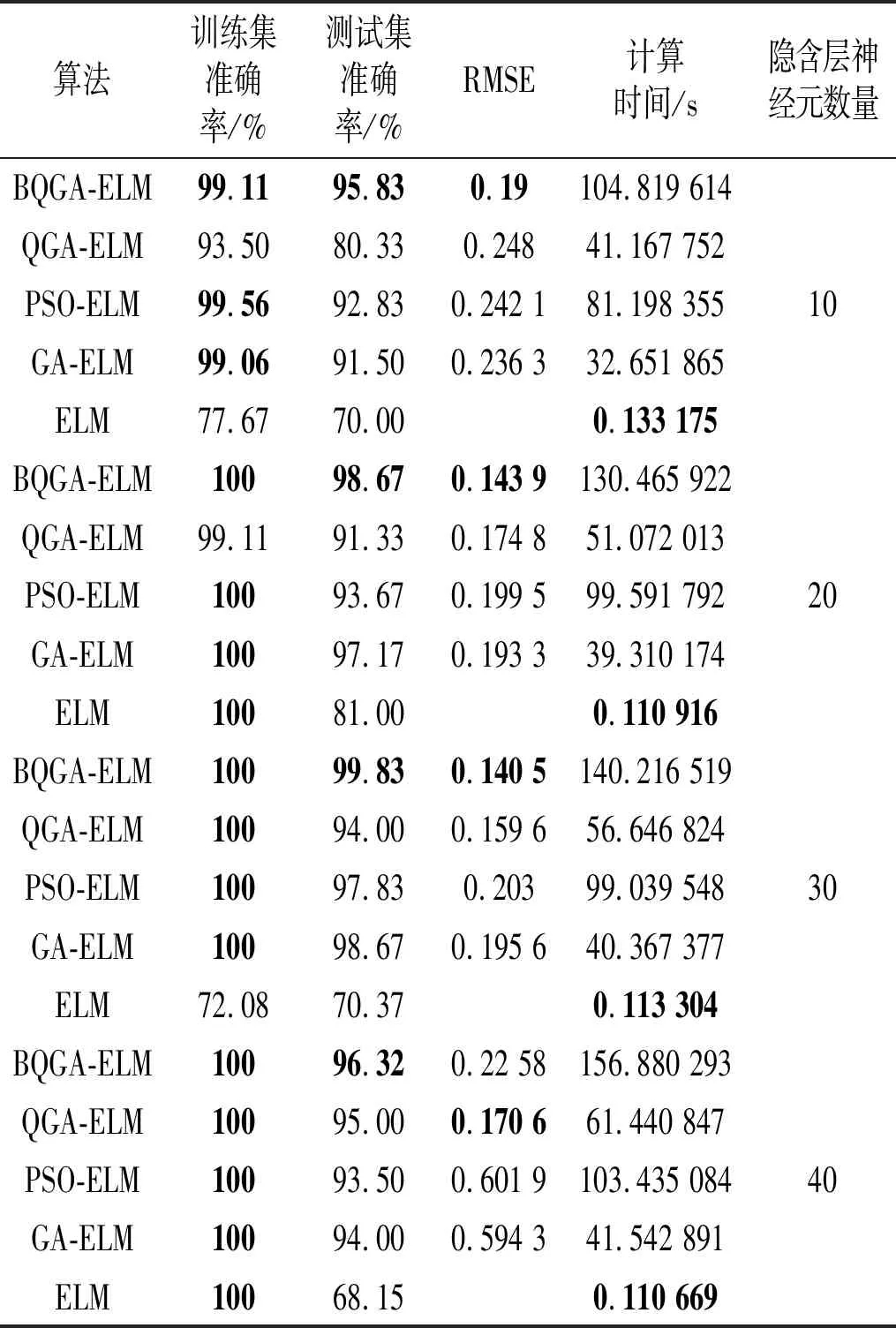
表7 不同診斷模型的平均診斷準確率

從表7的診斷結果可以看出，BQGA-ELM診斷模型對測試集樣本的平均診斷確率最高，校驗集RMSE收斂值也最低。當神經元數量為20，30和40時，診斷模型對訓練集樣本的診斷率均能達到最好，說明此時網絡對訓練集樣本利用充分，得到的訓練效果也最好；而這一結論也在測試集樣本中得到證明，除了ELM診斷模型之外，其它診斷模型對測試集樣本的平均診斷準確率均能達到90%以上。由于優化算法在尋優的過程，需要進行反復計算，因此被優化的ELM網絡診斷模型的診斷時間(=訓練時間+測試時間)均有所增加。但在實際故障診斷中，診斷模型先對故障樣本進行大量訓練，用訓練好的模型再去對故障進行診斷，因此會減少大量的計算時間(詳見“5.3”節)。因此，經過分析，BQGA-ELM相比于其它診斷模型，更加適用于滾動軸承故障診斷中。

5.2 誤差收斂

為進一步驗證BQGA-ELM診斷模型性能優于其它診斷模型，因此本小節從誤差收斂角度進行分析。當神經元數量為30時，幾種診斷模型誤差收斂如圖8所示。從圖8中可以發現，PSO-ELM和GA-ELM最先收斂，但收斂值卻較差，這表明GA和PSO可能陷入了局部極優，導致尋優終止；而BQGA-ELM和QGA-ELM能夠收斂到更小值，這得益于量子計算的并行性與搜索維度的增加。從誤差收斂角度分析，BQGA-ELM診斷模型的性能優于其它三者診斷模型。

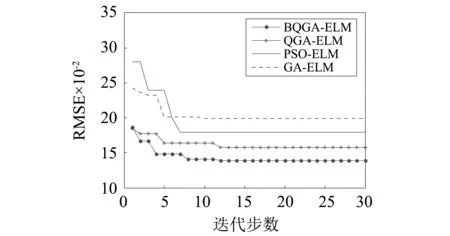
圖8 不同診斷模型的平均收斂誤差Fig.8 Average convergence error of different diagnostic models

5.3 診斷耗時

從表7中可以發現，除了ELM診斷模型，其它診斷模型計算時間均有所增加。表7中所給出的計算時間為訓練時間和測試時間之和，而實際故障診斷中，診斷模型都是在診斷訓練完成之后再對故障進行診斷。因此，在本小節中，分開統計訓練時間和診斷時間于表8中，并進行分析。從表8中可以看出，診斷模型訓練時間較長，但測試時間均較短。其中，由于BQGA相比于QGA增加了搜索維度，從而增加了量子染色體基因鏈的數量，這便導致計算量增加，尤其再重復運算過程中，時間累積效果更為明顯；但其診斷時間可以接受。ELM診斷模型訓練時間和診斷時間均較短，但其平均診斷準確率卻較低。同時，需要注意的是，診斷模型的訓練和診斷時間與計算機硬件設施存在一定的關系。因此，經過分析，BQGA-ELM診斷模型相比文中其它診斷模型更適宜于滾動軸承故障診斷。

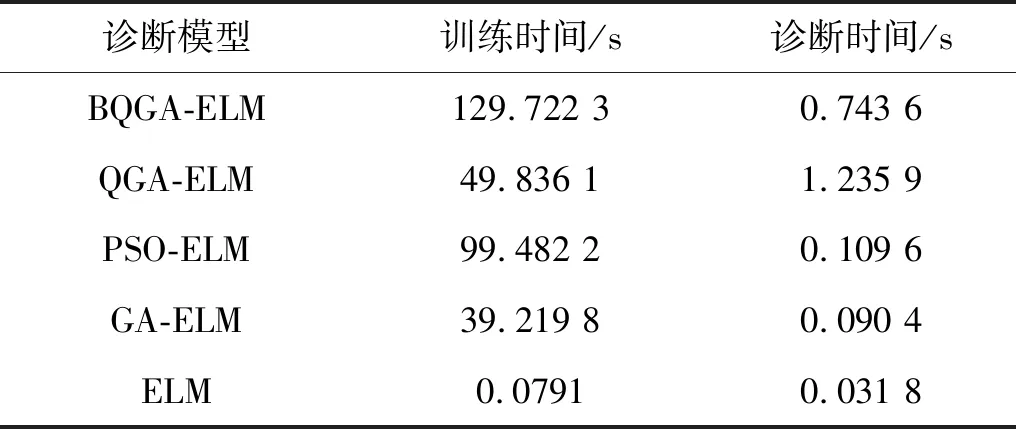
表8 平均計算時間

6 結 論

提出一種基于Bloch球面量子遺傳算法優化ELM網絡的診斷方法，利用BQGA并行、多維度的全局搜索能力，依據校驗集樣本的RMSE收斂情況，自適應的選擇ELM網絡的輸入權值和閾值，并將其應用于滾動軸承故障診斷中。通過仿真實驗，將BQGA-ELM，QGA-ELM，PSO-ELM，GA-ELM和ELM進行數據分類實驗對比，利用UCI標準數據中的兩組數據作為被測數據；仿真結果表明，BQGA-ELM在數據分類實驗中的有效性。

利用時域分析法提取實驗室采集到的軸承故障診斷振動信號的特征參量，并將其作為BQGA-ELM的輸入參數，進行滾動軸承故障診斷。診斷結果表明：BQGA-ELM在平均診斷準確率、誤差收斂性能以及故障診斷時間中均占據優勢。