基于靈敏度分析和不同數(shù)據(jù)融合的損傷識(shí)別方法

周俊賢， 呂中榮， 汪 利

(中山大學(xué) 工學(xué)院力學(xué)系，廣州 510006)

結(jié)構(gòu)損傷識(shí)別與健康檢測(cè)技術(shù)在世界范圍內(nèi)得到快速的發(fā)展和應(yīng)用，我國許多大型建筑上安裝了包括多種較大規(guī)模傳感器的健康監(jiān)測(cè)系統(tǒng)。在過去的十幾年里，國內(nèi)外研究者提出了大量基于振動(dòng)測(cè)試的損傷識(shí)別方法，如殘余力法、曲率模態(tài)法、模態(tài)應(yīng)變能法等一些經(jīng)典算法以及遺傳方法、人工蜂群算法等一些智能算法。結(jié)構(gòu)損傷識(shí)別往往被歸結(jié)為優(yōu)化問題，即通過定義一個(gè)目標(biāo)函數(shù)[1-2]，然后通過各種優(yōu)化算法來求得損傷參數(shù)。其中靈敏度方法是一種梯度類算法，與其他梯度法相比，其只需要計(jì)算一階靈敏度，且靈敏度方法有對(duì)小損傷比較敏感等優(yōu)勢(shì)，進(jìn)而受到了廣泛的關(guān)注。在實(shí)際工程中，最容易測(cè)量到的是模態(tài)數(shù)據(jù)，包括模態(tài)頻率和模態(tài)振型，其次是頻響數(shù)據(jù)和靜態(tài)數(shù)據(jù)。Farhat等[3]使用測(cè)試模態(tài)數(shù)據(jù)結(jié)合靈敏度分析對(duì)結(jié)構(gòu)進(jìn)行模型更新。Chen等[4]提出正則化的靈敏度方法，利用測(cè)量的不完全模態(tài)振型數(shù)據(jù)進(jìn)行模型更新。黃宗鵬等[5]由結(jié)構(gòu)的數(shù)值計(jì)算和試驗(yàn)測(cè)試得到的頻響函數(shù)，給出兩者的相關(guān)函數(shù)及其靈敏度的表達(dá)形式，提出了一種模型修正方法。楊辰等[6]基于靜力位移和固有頻率靈敏度矩陣，考慮這兩種動(dòng)靜測(cè)試數(shù)據(jù)，提出了融合靈敏度的結(jié)構(gòu)損傷識(shí)別方法。基于模態(tài)的識(shí)別方法，需要足夠的測(cè)試自由度同時(shí)依賴于模態(tài)識(shí)別的精度，這將增加測(cè)量工作量且在修正過程中引入了模態(tài)分析誤差，增加了修正的難度。基于頻響函數(shù)的模型修正方法，所必須的測(cè)試自由度較少，降低了測(cè)試工作量且不需要模態(tài)參數(shù)識(shí)別，降低了測(cè)試數(shù)據(jù)的誤差。但頻響函數(shù)需要構(gòu)造一個(gè)準(zhǔn)確合理的阻尼模型，且需要對(duì)所用的頻響曲線的頻率點(diǎn)和頻率段進(jìn)行精心的挑選。

本文提出了基于各類數(shù)據(jù)融合和靈敏度分析的損傷識(shí)別方法，將不同類型的測(cè)量數(shù)據(jù)通過加權(quán)融合到目標(biāo)函數(shù)中。算例表明，相對(duì)于僅考慮某一類數(shù)據(jù)的靈敏度方法，融合各類數(shù)據(jù)的靈敏度分析方法識(shí)別結(jié)果更加精確，抗噪能力更強(qiáng)。

1 理論方法

1.1 問題描述

剛度和質(zhì)量的改變會(huì)導(dǎo)致結(jié)構(gòu)頻率與振型等參數(shù)的變化，一般認(rèn)為損傷只引起剛度的改變，采用結(jié)構(gòu)模型中結(jié)構(gòu)單元?jiǎng)偠认禂?shù)的變化來表示結(jié)構(gòu)的損傷。結(jié)構(gòu)剛度矩陣可表示為

(1)

式中：K為損傷結(jié)構(gòu)的整體剛度矩陣；θi為單元?jiǎng)偠葥p傷系數(shù)；Ki為單元?jiǎng)偠染仃嚕籱為單元數(shù)目。

1.1.1 模態(tài)

考慮一個(gè)n自由度的結(jié)構(gòu)系統(tǒng)，通過有限元分析得到前n階特征值和振型Λr=〈λr,φr〉(r=1,2,…，n)。不考慮阻尼的結(jié)構(gòu)特征方程為

Kφr=λrMφr

(2)

式中：r=1,2,…,n為結(jié)構(gòu)的模態(tài)階數(shù)；M和K為結(jié)構(gòu)的質(zhì)量矩陣和剛度矩陣；λr為結(jié)構(gòu)的第r階特征值；φr為第r階振型，并已采用最大位移值的歸一化方法，將振型向量中各元素除以最大值。

1.1.2 頻響函數(shù)

黏性阻尼系統(tǒng)強(qiáng)迫振動(dòng)的復(fù)振動(dòng)方程為

(-Ω2M+iΩC+K)Z=F

(3)

式中：i為復(fù)數(shù)單位；Ω為外激勵(lì)的圓頻率;M,K和C為結(jié)構(gòu)的質(zhì)量矩陣，剛度矩陣和阻尼矩陣；Z和F為位移響應(yīng)復(fù)振幅列向量和外激勵(lì)幅值向量。

引入位移頻響函數(shù)矩陣H=(-Ω2M+iΩC+K)-1，則結(jié)構(gòu)復(fù)振幅響應(yīng)可以根據(jù)式(3)表述為

Z=HF

(4)

若激勵(lì)為頻域內(nèi)作用于結(jié)構(gòu)第j個(gè)自由度上的單位諧波激勵(lì)，則式(4)可以簡(jiǎn)化為Z=Hj，Hj為位移頻響矩陣的第j列。

1.1.3靜力位移

靜位移方程為

Ku=F

(5)

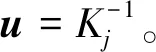
1.2 模型修正問題的目標(biāo)函數(shù)

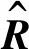
(6)

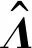
在損傷識(shí)別問題中，模型修正的目標(biāo)函數(shù)就是使測(cè)量數(shù)據(jù)和計(jì)算數(shù)據(jù)的殘差最小，見式(7)

(7)

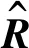
1.3 基于靈敏度的損傷識(shí)別方法

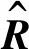
(8)

式中：Rk=R(θk)為第k次迭代的計(jì)算數(shù)據(jù)；Sk=S(θk)為第k次迭代中的靈敏度矩陣；Δθk為第k次迭代中的損傷參量更新值。

目標(biāo)函數(shù)式(7)變?yōu)?/p>

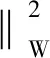
(9)

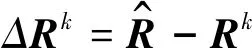
當(dāng)θ的維數(shù)遠(yuǎn)大于測(cè)點(diǎn)數(shù)目，即未知數(shù)遠(yuǎn)多于方程數(shù)時(shí)，式(9)為一病態(tài)的線性方程組，因此引入Tikhonov正則化方法[7]，新的目標(biāo)函數(shù)為

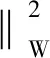
(10)

式中:λ為正則化系數(shù)，其值用L-曲線法[8]計(jì)算。當(dāng)測(cè)量數(shù)據(jù)遠(yuǎn)大于θ的元素個(gè)數(shù)時(shí)，λ趨近于0，這時(shí)式(10)就接近于原來的目標(biāo)函數(shù)式(9)。求解式(10),得到

Δθk=(SkTWSk+λI)-1SkTWΔRk

(11)

第k次迭代的參數(shù)θk+1表達(dá)式為

θk+1=θk+Δθk

(12)

1.4 增強(qiáng)的靈敏度方法迭代算法步驟

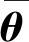
(13)

當(dāng)算得的ρ大于一個(gè)臨界值ρcr時(shí)，才表征線性化的目標(biāo)函數(shù)與原目標(biāo)函數(shù)有良好的吻合度。事實(shí)上，提高Tikhonov正則化參數(shù)λ某程度上等同于提高吻合度指標(biāo),表1為增強(qiáng)的靈敏度方法的具體步驟。

表1 增強(qiáng)的靈敏度方法的具體步驟Tab.1 Algorithmic details for enhanced response sensitivity approach

2 靈敏度分析與數(shù)據(jù)加權(quán)融合

2.1 靈敏度分析

針對(duì)不同的數(shù)據(jù)類型，靈敏度分析各不相同。

特征值靈敏度

(14)

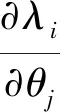
振型靈敏度

(15)

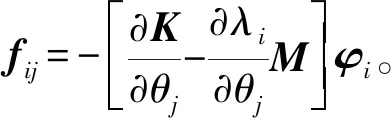
可以證得[K-λiM]秩為n-1，所以

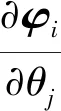
(16)

式中：v為特解；φ為對(duì)應(yīng)的齊次方程的通解。

假設(shè)第i階振型的第k個(gè)元素絕對(duì)值最大，為1，令系數(shù)矩陣[K-λiM]的對(duì)應(yīng)行和對(duì)應(yīng)列為0，坐標(biāo)為(k,k)的元素等于1，fij的第k個(gè)元素為0，矩陣表示為

(17)

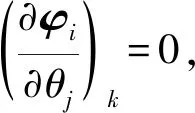
頻響函數(shù)靈敏度

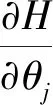
(18)

靜力位移靈敏度

(19)

最后根據(jù)測(cè)量數(shù)據(jù)組裝靈敏度矩陣

(20)

2.2 數(shù)據(jù)的加權(quán)與融合

當(dāng)采用不同數(shù)據(jù)時(shí)，要考慮不同數(shù)據(jù)間的影響，一方面，數(shù)據(jù)間的單位不同，無法做到量綱統(tǒng)一，如采用模態(tài)特征值與靜位移數(shù)據(jù)時(shí)，特征值數(shù)值較大，當(dāng)靜力位移數(shù)據(jù)量很少時(shí)，目標(biāo)函數(shù)中起主導(dǎo)作用的是特征值的殘差，靜力位移的影響有限；其次，當(dāng)采用不同單位時(shí)，也有不同的影響，如靜力位移數(shù)據(jù)，當(dāng)采用mm為單位時(shí)比采用m為單位時(shí)對(duì)結(jié)果的影響較大，因?yàn)楫?dāng)采用mm為單位時(shí)，靜力位移的數(shù)據(jù)數(shù)值較大。此外，即使采用同類數(shù)據(jù)，數(shù)據(jù)受到的噪聲水平并不相同，一部分?jǐn)?shù)據(jù)的測(cè)量誤差較大，一部分?jǐn)?shù)據(jù)的測(cè)量誤差較小。

所以參數(shù)的權(quán)重矩陣W應(yīng)該要能反應(yīng)參數(shù)和測(cè)量數(shù)據(jù)的不確定程度[9-10]。Link[11]把權(quán)重矩陣與平方靈敏度矩陣聯(lián)系在一起。Friswell等將權(quán)重矩陣取為測(cè)量協(xié)方差矩陣的逆矩陣。

當(dāng)僅考慮測(cè)量誤差，不考慮模型誤差的情況下，加權(quán)矩陣W取為測(cè)量數(shù)據(jù)協(xié)方差QR的逆矩陣時(shí)，計(jì)算得到的識(shí)別誤差的平方期望E[(θ-θex)T(θ-θex)]最小。

證明如下：

目標(biāo)函數(shù)式(7)進(jìn)一步線性化為

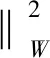
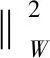
(21)

式中：εR為測(cè)量誤差；S=S(θex);h.o.t為可以忽略的高階項(xiàng)。當(dāng)θ在θex附近的，可以解得

θ-θex≈[STWS]-1STWεR=LWεR

(22)

式中：LW=[STWS]-1STW。可以得到

E[(θ-θex)T(θ-θex)]≈

(23)

式中：tr(·)為跡算子。

由于加權(quán)矩陣W被包含在輔助矩陣LW里，所以我們選擇直接尋找一個(gè)最優(yōu)的LW。

引入拉格朗日算子Θ

(24)

式中：L(LW,Θ)為拉格朗日方程。式(24)對(duì)LW作最小化處理，得到

(25)

結(jié)合LWS=I和式(25)得到

(26)

結(jié)合式(25)，最優(yōu)矩陣LW為

(27)

把此時(shí)的權(quán)重矩陣W稱為最優(yōu)權(quán)重Wopt

(28)

觀測(cè)當(dāng)權(quán)重矩陣時(shí)為最優(yōu)加權(quán)時(shí)，目標(biāo)函數(shù)變?yōu)?/p>

(29)

式中：σΛ，σH和σu分別為模態(tài)數(shù)據(jù)、頻響函數(shù)數(shù)據(jù)和靜力位移數(shù)據(jù)的標(biāo)準(zhǔn)差。經(jīng)過權(quán)重處理后，噪聲誤差大的數(shù)據(jù)，對(duì)結(jié)果的影響變小；另一方面，權(quán)重處理起到一個(gè)去量綱的作用，使得各類數(shù)據(jù)之間取得一個(gè)平衡。

3 算 例

用數(shù)值模擬的數(shù)據(jù)來代替實(shí)測(cè)數(shù)據(jù)，并給數(shù)據(jù)加上高斯噪聲，加載噪聲的方式為

(30)

式中：λ,φ,H,u為R(θex);eλ,eφ,eH,eu為對(duì)應(yīng)的噪聲水平；Randλ,Randφ,RandH,Randu為對(duì)應(yīng)的正態(tài)分布矩陣。

3.1 平面桁架

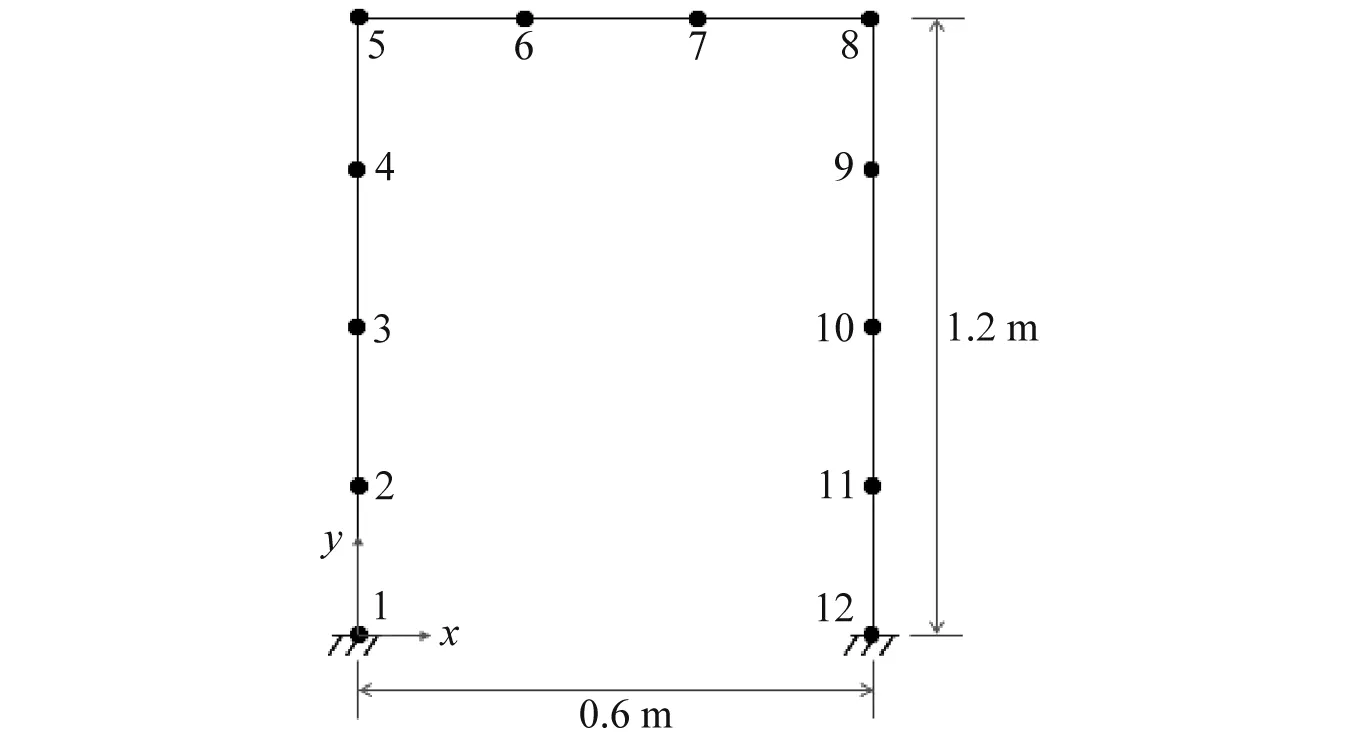
圖1 平面框架模型Fig.1 A plane frame model

圖1為單跨平面桁架，高1.2 m，寬0.6 m，邊界條件為左右兩邊固支。楊氏模量E=69 GPa,密度ρ=2.7×103kg·m-3，橫截面尺寸為b=0.01 m和h=0.02 m。

工況1：?jiǎn)卧?受損25%。

工況2：?jiǎn)卧?、單元6、單元10分別受損10%，15%，10%。

每種情況分別在隨機(jī)產(chǎn)生的20組數(shù)據(jù)下得到識(shí)別結(jié)果，然后取識(shí)別的平均值和標(biāo)準(zhǔn)差，來觀察方法抗噪的能力，結(jié)果如圖2和圖3所示。可以看到當(dāng)采用混合數(shù)據(jù)但不加權(quán)的情況下，識(shí)別誤差十分的大，如工況1的單元3識(shí)別結(jié)果；而采用經(jīng)過加權(quán)處理的混合數(shù)據(jù)的識(shí)別結(jié)果比單獨(dú)使用某類數(shù)據(jù)的識(shí)別結(jié)果要好，標(biāo)準(zhǔn)差要更小，反應(yīng)了抗噪能力更強(qiáng)。

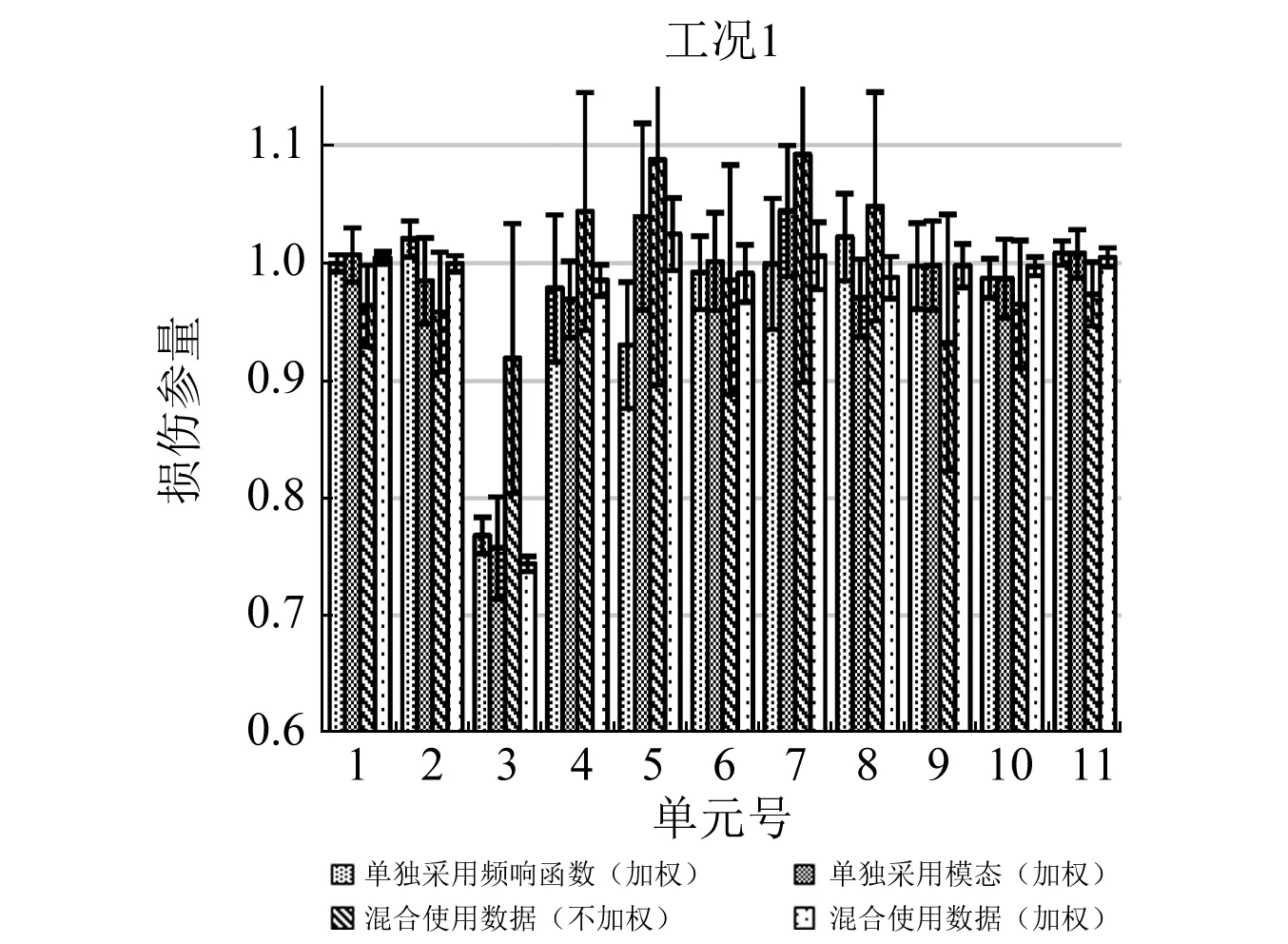
圖2 工況1損傷識(shí)別的均值與標(biāo)準(zhǔn)差的條形圖Fig.2 Bar graph with means and standard deviations for damage identification of scenario 1

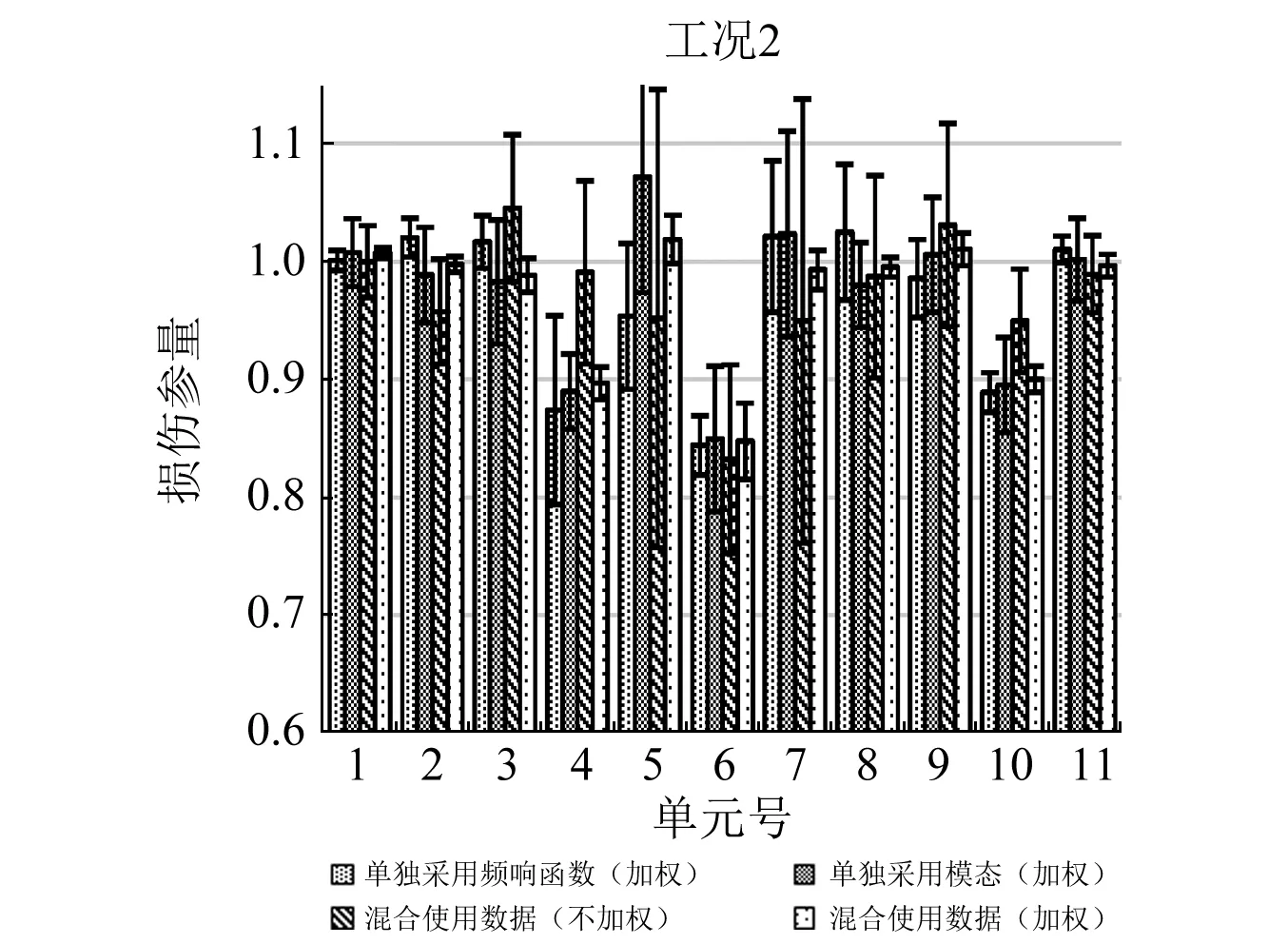
圖3 工況2損傷識(shí)別的均值與標(biāo)準(zhǔn)差的條形圖Fig.3 Bar graph with means and standard deviations for damage identification of scenario 2

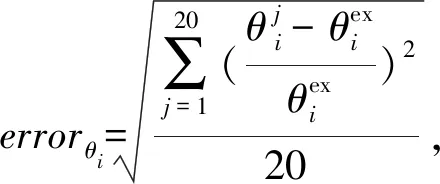
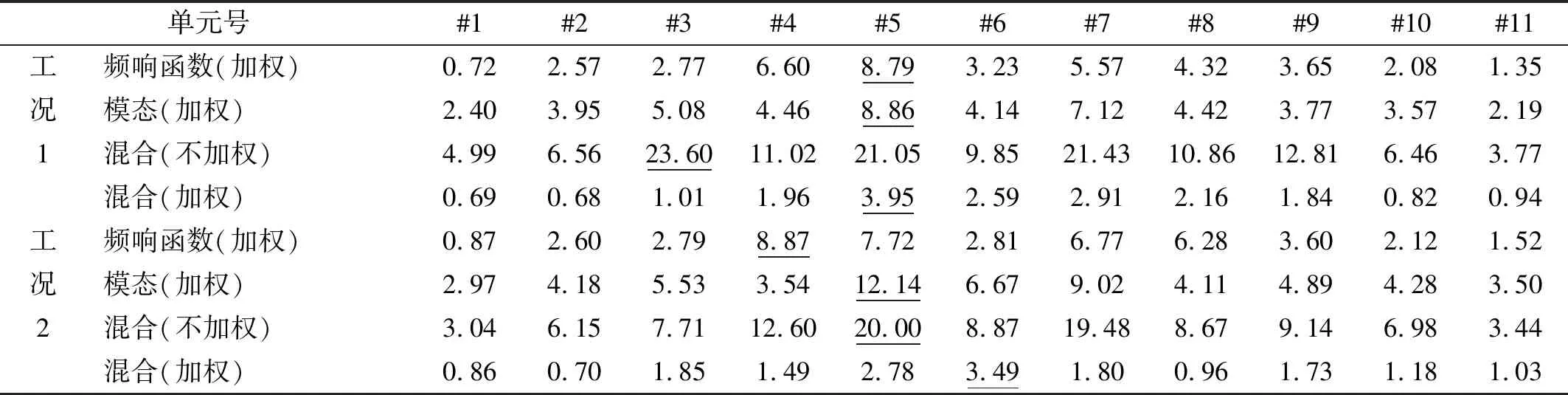
表2 單元?jiǎng)偠葥p傷參數(shù)的平均相對(duì)誤差Tab.2 The relative error of the damage parameters %

3.2 板

單跨板邊界條件為左右兩邊簡(jiǎn)支，尺寸見圖4。楊氏模量E=25 GPa,密度ρ=2.8×103kg·m-3，泊松比υ=0.2。有限元建模中，將板劃分30個(gè)4結(jié)點(diǎn)Reissner-Mindlin板單元。模型修正中的參數(shù)個(gè)數(shù)等于有限元單元數(shù)。

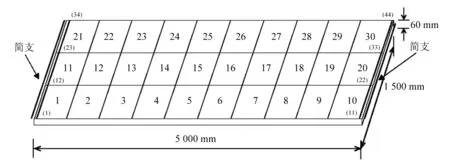
圖4 單跨簡(jiǎn)支板模型Fig.4 A single-span simple-support plate model

工況3：?jiǎn)卧?,單元18，單元23分別受損10%，20%，10%。

用式(27)計(jì)算每個(gè)單元的損傷參數(shù)的平均相對(duì)誤差，結(jié)果如圖5～圖8所示。可以看到單獨(dú)使用頻響函數(shù)的最大平均誤差為8.88%,因?yàn)殪o力位移數(shù)據(jù)較頻響函數(shù)少，所以單獨(dú)使用靜力位移數(shù)據(jù)的最大平均相對(duì)誤差為20.63%,采用不加權(quán)的混合數(shù)據(jù)最大平均相對(duì)誤差最大為33.24%，混合使用加權(quán)處理數(shù)據(jù)的最大平均相對(duì)誤差下降為3.5%，再次證明了對(duì)不同數(shù)據(jù)進(jìn)行加權(quán)的重要性。

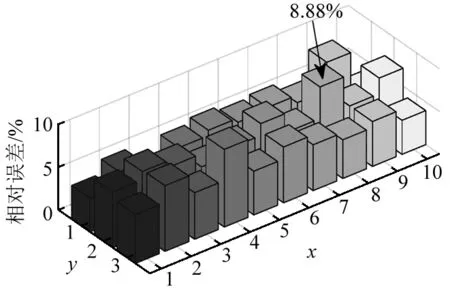
圖5 使用頻響函數(shù)的單元損傷參數(shù)相對(duì)誤差平均值Fig.5 Relative errors for damage parameters obtained with using frequency response function

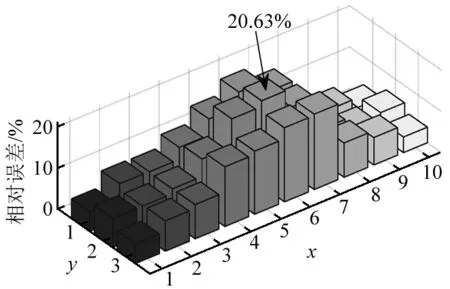
圖6 使用靜力位移的單元損傷參數(shù)相對(duì)誤差平均值Fig.6 Relative errors for damage parameters obtained with using static data

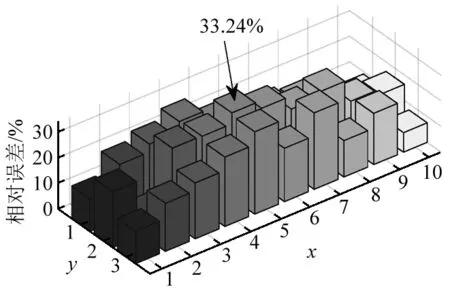
圖7 用混合數(shù)據(jù)(不加權(quán))的單元損傷參數(shù)相對(duì)誤差平均值Fig.7 Relative errors for damage parameters obtained with using unweighted hybrid data

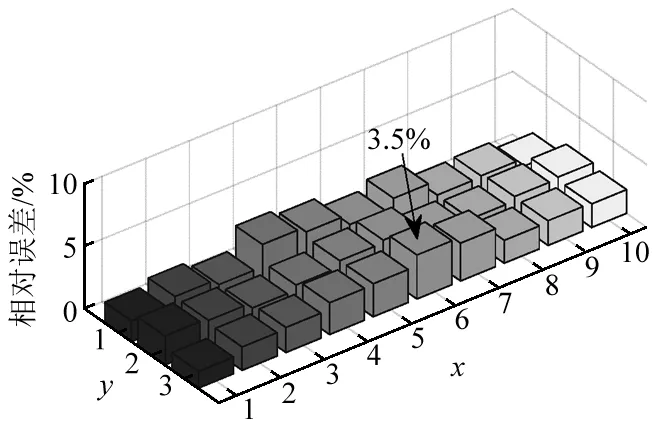
圖8 用混合數(shù)據(jù)(加權(quán))的單元損傷參數(shù)相對(duì)誤差平均值Fig.8 Relative errors for damage parameters obtained with using weighted hybrid data

4 結(jié) 論

本文采用基于靈敏度和多種數(shù)據(jù)加權(quán)混合的有限元模型識(shí)別法對(duì)結(jié)構(gòu)的局部損傷進(jìn)行識(shí)別，該方法包含了對(duì)不同數(shù)據(jù)的靈敏度分析以及令識(shí)別誤差的平方期望最小的最優(yōu)加權(quán)等理論，通過一階泰勒線性展開、靈敏度分析和正則化對(duì)識(shí)別方程進(jìn)行迭代求解得到識(shí)別結(jié)果。兩個(gè)數(shù)值算例表明提出的加權(quán)混合數(shù)據(jù)比起單一使用某種數(shù)據(jù)識(shí)別的結(jié)果更加準(zhǔn)確，損傷識(shí)別精度高，對(duì)模擬的測(cè)量噪聲不大敏感的優(yōu)點(diǎn)，具有較好的工程應(yīng)用潛力。其優(yōu)勢(shì)主要體現(xiàn)與：

(1)單獨(dú)使用某種數(shù)據(jù)時(shí)，數(shù)據(jù)量不夠多，如模態(tài)數(shù)據(jù)往往只能得到前幾階頻率和不完整振形，不足以識(shí)別多參數(shù)的大型結(jié)構(gòu)。

(2)單獨(dú)使用某種數(shù)據(jù)時(shí)，容易受到結(jié)構(gòu)的模型誤差影響，如頻響函數(shù)會(huì)受到結(jié)構(gòu)阻尼誤差的影響，而模態(tài)、靜力位移數(shù)據(jù)則不受其影響。

(3)通過最優(yōu)加權(quán)使不同數(shù)據(jù)取得一種去量綱化的效果，使不同數(shù)據(jù)對(duì)識(shí)別結(jié)果的影響得到平衡。