基于跟蹤誤差模型的智能車輛軌跡跟蹤方法*

潘世舉，李 華，蘇致遠，徐友春

（陸軍軍事交通學院，天津 300161）

前言

隨著人工智能和機器人技術的不斷進步，智能車輛技術迅速發展。其關鍵技術主要包括精確定位技術、環境感知技術、規劃決策和控制技術等［1-3］。軌跡跟蹤技術［4-7］主要是控制車輛的橫縱向運動，使車輛沿著參考軌跡行駛，其精確程度直接決定了智能車輛的行為表現。

近年來許多學者針對參考軌跡跟蹤問題進行了研究。文獻［8］中通過車載傳感器實時獲取行駛軌跡相對于最優路徑的偏差信息，采用偏差融合技術的PID控制方法（proportion integration differentiation control），實現鏟運車的無人駕駛控制。文獻［9］中采用改進的有限時間最優預瞄橫向控制算法，其車輛相對于軌跡的橫向偏差在±0.3 m內，但預瞄時間的選取較為繁瑣。文獻［10］中采用基于模糊控制和自校正模型控制方法，實現插秧機以1 m/s行駛時，平均橫向偏差為8.7 cm。文獻［11］中基于迭代學習控制理論設計迭代學習控制算法，該算法實現了車輛期望路徑有限區間內的高精度完全跟蹤控制，但僅適用于參考軌跡重復固定的情況。

隨著現代控制理論的發展，模型預測控制理論引起了人們的關注。文獻［12］中以車輛非線性運動學模型為基礎設計控制器，以低于1 m/s的速度跟蹤圓形路徑時，橫向最大誤差小于0.1 m。文獻［13］中采用車輛動力學模型設計控制器，以15 km/h的速度跟蹤軌跡時，可將誤差控制在0.2 m范圍內。

為進一步提高智能車輛軌跡跟蹤精度，本文中采用基于車輛動力學的跟蹤誤差模型設計模型預測控制器，在Carsim與MATLAB/Simulink構建的聯合仿真平臺中進行仿真實驗，并進行了實車驗證，以15 m/s的速度跟蹤軌跡時，橫向最大誤差在0.52 m范圍內，跟蹤效果較為理想。

1 車輛動力學模型

采用車輛四輪模型分析車輛在運動過程中的受力情況，為簡化計算，假設車輛在水平路面上行駛，車輛縱向速度恒定，不考慮橫向和縱向空氣阻力，前輪轉角較小。滿足以上條件的車輛動力學模型如圖1所示，其中，xoy為車體坐標系，坐標原點o為車輛質心所在點，x軸正方向為車頭方向，y軸正方向為垂直車體方向向左，z軸正方向為垂直xoy面向上，XOY為慣性坐標系。

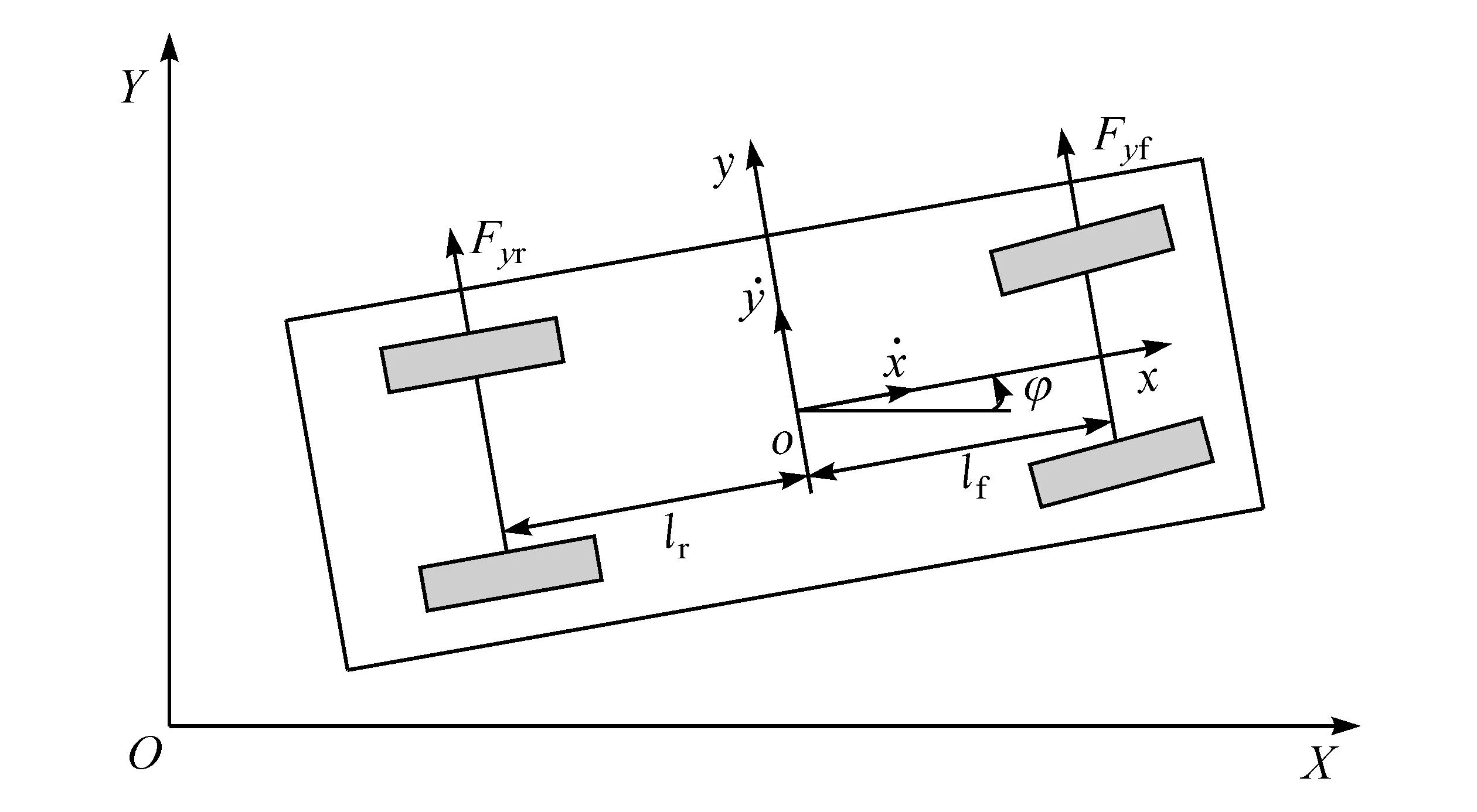
圖1 車輛模型

考慮車輛側向受力和橫擺運動，建立如下動力學方程：

式中：m為車輛的質量；φ為車輛在慣性坐標系下的航向；Fyf，Fyr分別為車輛前、后輪受到的側向力；Iz為車輛繞z軸的轉動慣量；lf，lr分別為車輛前、后軸中心到質心的距離。

在小角度假設下，前、后輪受到的側向力為

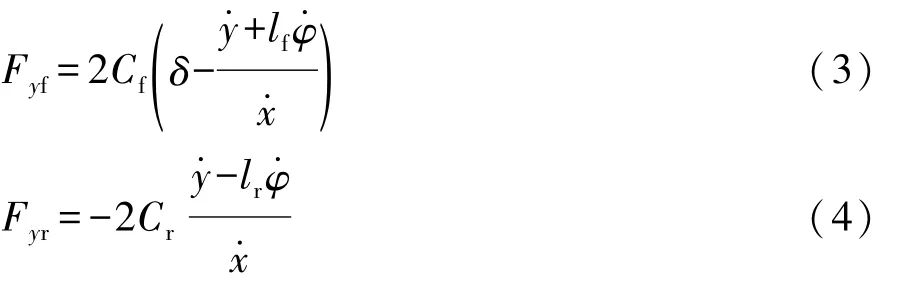
式中：Cf，Cr分別為前、后輪側偏剛度；δ為前輪轉角。聯合式（1）～式（4），可得

智能車輛的軌跡跟蹤問題是指在慣性坐標系中，設計軌跡跟蹤控制器，確定車輛控制輸入，使車輛在規定的時刻到達預設的軌跡點，并具備預設的狀態，包括位置、航向、速度、加速度等。因此，還應考慮車輛的縱向控制。本文中采用如下車輛縱向運動學方程：

式中：a為車輛的加速度；ar為參考點的加速度；s為車輛相對于軌跡起點的位置；sr為參考點相對于軌跡起點的位置。

定義車輛在參考軌跡跟蹤過程中產生的跟蹤誤差：e1為車輛質心與參考點的橫向誤差，e2為車輛與參考點的航向誤差［14］，e3為車輛與參考點的距離誤差，則

綜合式（5）～式（10），可得到基于參考軌跡的車輛模型為

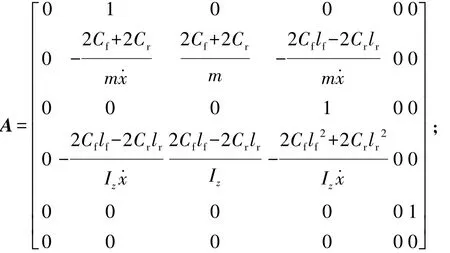
可以看出，該系統為非線性系統，為提高模型預測控制計算速度，還需進行線性化和離散化處理。

2 線性時變誤差模型

參考軌跡上的任意點均滿足式（11），即

其中，由于參考點處于參考軌跡上，則參考狀態量 ξr=［0 0 0 0 0 0］T。將式（12）在該點處進行一級泰勒展開，忽略高級項，得

式中：fξ，r為 f相對于 ξ的雅克比矩陣，fu，r為 f相對于u的雅克比矩陣，fw，r為f相對于w的雅克比矩陣。

將式（13）與式（12）相減得

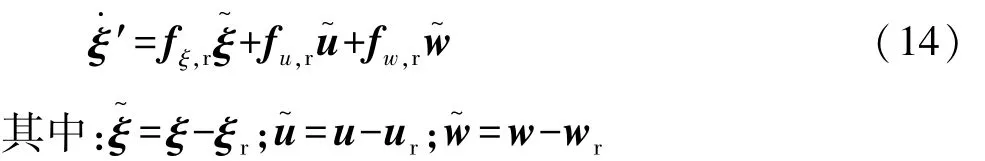
假設預測時域為Np，系統采樣時間為k=0，…，Np，系統采樣周期為T。車輛的底層控制器會在一個控制周期T內保持控制量的恒定，因此采用零階保持進行離散的方法能夠得到比較精準的符合期望的控制輸入量。設計增廣向量z=［ξ u w］T，則式（14）可表示為

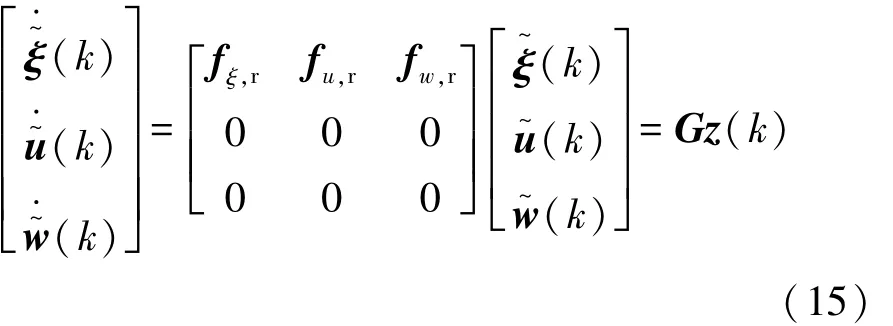
對Gz進行矩陣指數運算，采取零階保持可得

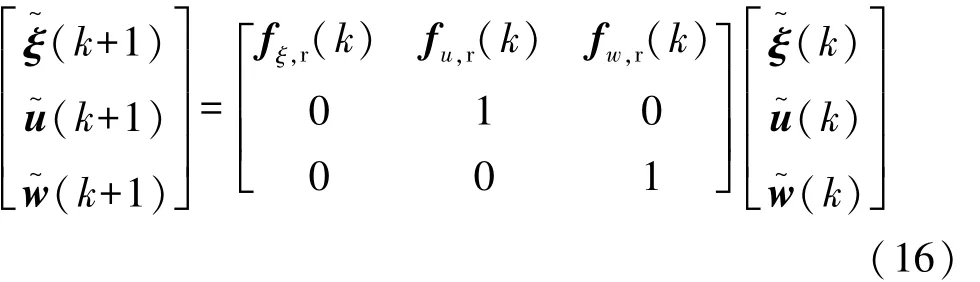
式中第一行即為車輛的線性時變誤差模型：

3 軌跡跟蹤控制器設計

3.1 預測模型

定義預測時域Np內的車輛的預測輸出矩陣、控制量矩陣和附加變量矩陣為

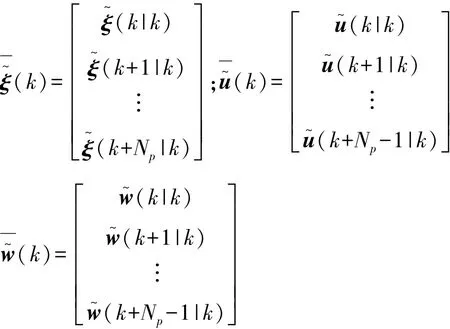
根據式（17），可推導出系統的預測方程為

式中：系統狀態量預測參數為

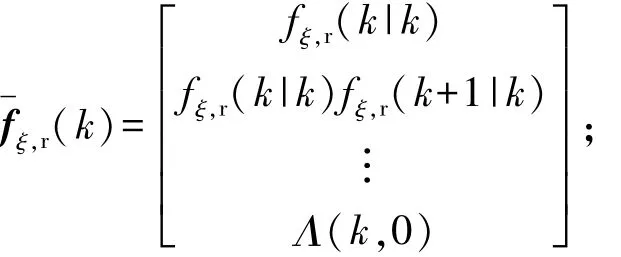
控制量矩陣預測參數為

附加變量預測參數為

3.2 滾動優化

滾動優化是對系統狀態量和控制量的優化，使得車輛能夠快速平穩地實現軌跡跟蹤，通過目標函數的最優來實現。式（18）中，u～表示的系統控制量未知，可通過設定目標函數進行求解。采用控制增量作為優化目標函數的狀態量，同時引入松弛因子，保證系統存在可行解。目標函數表達式為

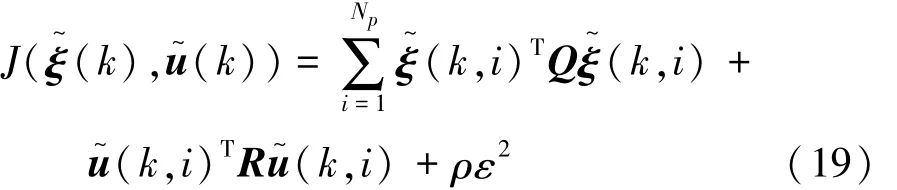
式中：Q為預測時域權重矩陣；R為控制時域權重矩陣；ρ為權值系數；ε為松弛因子。目標函數第1項表示對參考軌跡的快速跟蹤能力，第2項表示對控制量變化的優化能力。將式（18）代入式（19），轉化為二次規劃問題，并考慮系統狀態量、控制量和控制增量的約束條件，整理得

式中：Hk為正定Hessian矩陣；Gk為控制量系數矩陣；Pk為常數；E（k）為預測時域內系統跟蹤誤差；ξmin和 ξmax為狀態量約束最值；umin和 umax為控制量約束最值；Δumin和Δumax為控制增量約束最值。

3.3 反饋校正

在采樣時刻k，采用有效集方法進行求解，求取性能指標 J（ξ～（k），u～（k））的最小值，獲得最優的控制序列｛u～（k|k），…，u～（k+Np-1|k）｝，取第 1項作為控制增量，計算控制輸入量：

在（k+1）時刻，重新計算最優控制序列并將第1項控制增量作用于系統，從而實現最優控制。

4 實驗結果與分析

4.1 仿真實驗

4.1.1 仿真平臺介紹

該仿真平臺由CarSim提供車輛動力學模塊，通過MATLAB語言編寫 S-Function作為控制器，在Simulink中進行整體結構的搭建。

本文中CarSim車輛動力學模型整車質量為1 100 kg，質心與前、后軸中心的距離分別為1 040和1 560 mm，質心高度為540 mm，輪距為1 695 mm，路面附著系數為0.8，滾動阻力系數為0.8。

4.1.2 參考軌跡生成

在軌跡跟蹤驗證中通常使用雙移線進行測試，但標準雙移線工況彎道不足以平滑，不易在仿真中應用。本文中借鑒文獻［15］中的雙移線工況對所建立的控制器進行驗證，函數表達為

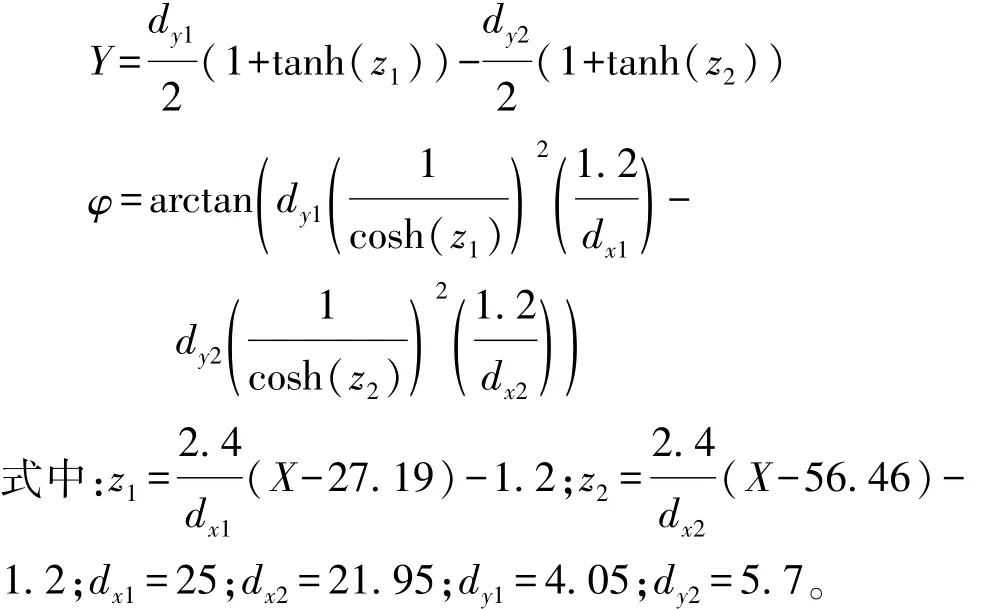
以10 m/s的速度跟蹤參考軌跡為例，進行控制器參數調試。隨著預測時域的增大，橫向跟蹤誤差減小，主要是因為預測時域較大時，控制器能夠更好地預測系統未來輸出，根據當前誤差及時修正系統輸入信號，但同時會增加計算量；控制時域的變化對控制器跟蹤效果影響較小，主要是因為反饋校正控制器僅將控制增量的第1個元素作用于系統；隨著控制周期變長，橫向跟蹤誤差逐漸減小。仿真控制器參數設置如表1所示。

4.1.3 軌跡跟蹤實驗

在慣性坐標系下，車輛初始狀態為：x=0，y=0，v=0，φ=0，δ=0。采用非線性MPC控制器和本文中設計的線性MPC控制器，以10 m/s的速度進行軌跡跟蹤，仿真跟蹤結果如圖2所示。線性MPC控制器的橫向最大誤差為0.517 m，航向最大誤差為0.053 rad；非線性MPC控制器的橫向最大誤差為1.496 m，航向最大誤差為0.124 rad。保持車輛初始狀態不變，采用本文中設計的MPC控制器，分別以5，10和15 m/s的速度進行軌跡跟蹤，仿真跟蹤結果如圖3和圖4所示，其中橫向最大誤差分別為0.452，0.517和0.292 m，航向最大誤差分別為0.059，0.053和0.067 rad，側向最大加速度分別為 0.619，2.585和6.298 m·s-2。

表1 仿真控制器參數

4.2 實車實驗

4.2.1 實驗平臺介紹

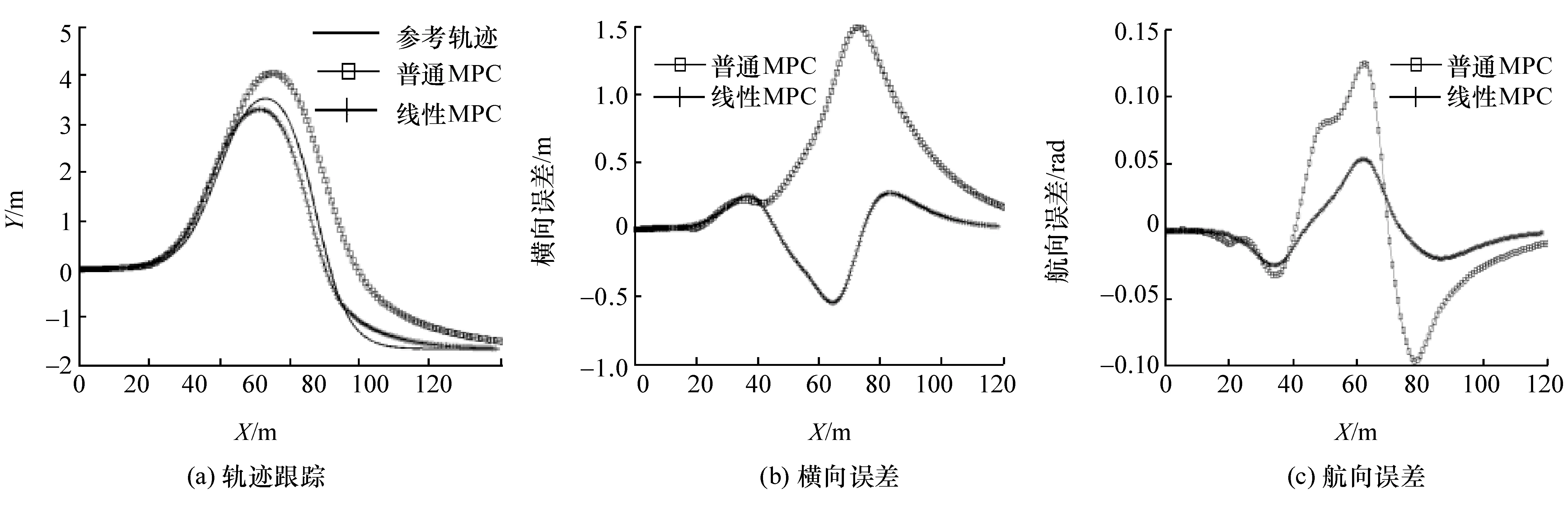
圖2 線性MPC與普通MPC跟蹤效果對比

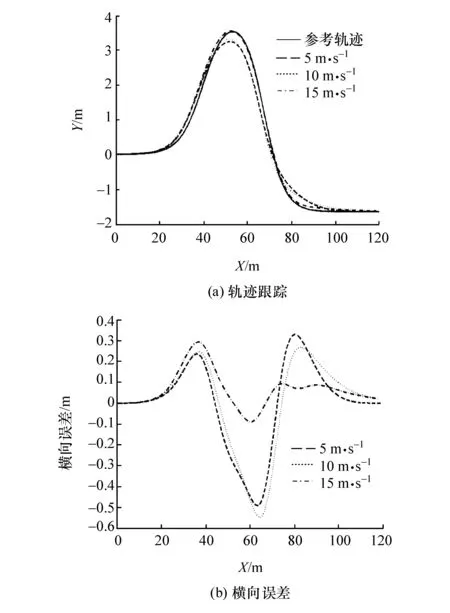
圖3 軌跡跟蹤與橫向誤差

圖4 航向誤差與側向加速度

實車實驗平臺為 JJUV8，該平臺改裝于長城Wey。硬件架構分為底層、交換層、感知層和計算層。底層主要包含執行機構驅動電路、車輛信號控制電路和中控管理電路；交換層主要包含交換機；感知層包括64線激光雷達、16線激光雷達、組合慣導、攝像頭和毫米波雷達；計算層部分包含兩臺工控機。軟件架構包括感知、預測、決策規劃和控制4部分，各部分并行計算，利用機器人操作系統的消息發布和訂閱機制進行數據交互。

決策規劃部分根據感知、預測部分發送的環境信息和車輛自身狀態等，實時規劃可行駛軌跡，周期為0.1 s；控制部分根據車輛自身狀態與參考軌跡的誤差計算控制量，周期為0.02 s。初始時，車輛質心位置與參考軌跡起點重合，航向與參考軌跡初始方向一致。實驗平臺和顯示界面如圖5所示，其中方框為車輛位置，曲線為參考軌跡。JJUV8實驗平臺參數如表2所示。

表2 JJUV8實驗平臺參數

圖5 實驗平臺和軌跡顯示界面

4.2.2 軌跡跟蹤實驗

軌跡跟蹤實驗中，為保證軌跡跟蹤實車實驗的可操作性和安全性，在天津空港經濟區選取一條道路空曠、車輛和行人較少且路面情況滿足要求的道路進行實驗，如圖5所示。車輛以5和10 m/s的速度分別進行3次實驗取其平均值，實車實驗跟蹤結果如圖 6所示，橫向最大誤差分別為 0.61和0.45 m，航向最大誤差分別為0.05和0.06 rad，側向最大加速度分別為0.54和3.72 m·s-2。

4.3 實驗分析

（1）本文中設計的線性 MPC控制器與普通MPC控制器的仿真實驗結果相比，橫向最大誤差減少0.98 m，航向最大誤差減少0.071 rad。主要原因是在求解最優解方程的過程中，方程包含了多個最優變量和非線性狀態約束，以及由控制量約束和狀態量約束組成的線性約束，對于非線性MPC，其求解的復雜程度隨系統狀態方程階數的增加而迅速增加，運算時間增加，很難保證實時控制，從而導致跟蹤誤差增大。

圖6 實車軌跡跟蹤結果

（2）軌跡跟蹤仿真實驗結果中，對于5和10 m/s跟蹤速度，橫向最大誤差隨速度增大而增大，航向最大誤差隨速度增大而減小，主要原因是轉彎時車輛質心變化導致繞z軸的轉動慣量發生變化、前輪轉角較大導致小角度假設不成立，控制器預測的車輛運動與實際情況差別增大。15 m/s跟蹤速度下橫向最大誤差較小，航向最大誤差較大，主要原因是轉彎處的側向最大加速度大于0.4g，輪胎側偏特性處于非線性范圍、左右車輪載荷變化導致的特性變化等。

（3）軌跡跟蹤實車實驗結果與仿真實驗相比，5 m/s跟蹤速度下的橫向最大誤差增加0.15 m，而航向最大誤差減小0.01 rad，主要原因是傳感器、執行器和路面不平坦等不確定因素對系統的干擾。10 m/s跟蹤速度下的橫向最大誤差減少0.07 m，航向最大誤差增加0.08 rad，主要原因是在仿真環境中路面附著系數和滾動阻力系數均為0.8，而實車實驗道路環境相對較差。

5 結論

本文中以車輛動力學模型為基礎，提出基于線性時變模型預測控制的軌跡跟蹤方法，設計控制器并進行仿真實驗與實車實驗。仿真實驗結果表明，該控制器與普通非線性MPC控制器相比，能夠滿足實時控制的要求，且跟蹤效果更優。在雙移線軌跡跟蹤過程中，5 m/s時橫向最大誤差為0.452 m，10 m/s橫向最大誤差為0.517 m。

利用JJUV8平臺進行實車驗證，車輛以5 m/s速度跟蹤軌跡時，與仿真實驗相比，橫向最大誤差增加0.15 m，航向最大誤差減小0.01 rad，基本滿足軌跡跟蹤的要求。車輛以10 m/s速度跟蹤軌跡時，橫向最大誤差為0.45 m，航向最大誤差為0.06 rad。本文中所設計的控制器效果較為理想，能夠滿足智能車輛的軌跡跟蹤要求。

下一步工作將繼續研究車輛在縱向速度變化、載荷轉移情況下的動力學模型，分析低附著系數和低滾動摩擦因數環境下的控制方法，兼顧車輛運動穩定性，并展開實車實驗。