本征正交分解在發動機缸內流場擬序結構研究中的應用*

秦文瑾，齊觀超，汪 濤，周 磊，賈 明，解茂昭

（1.上海理工大學機械工程學院，上海 200093； 2.天津大學，內燃機燃燒學國家重點實驗室，天津 300072；3.大連理工大學能源與動力學院，大連 116024）

前言

發動機工作時，缸內存在復雜的物理化學現象，相互之間強烈耦合。所有過程的發生均依托于缸內湍流場，可見對缸內湍流場的科學認識是正確理解其他物理化學現象的前提。湍流場內分布著各種不同尺度的渦團結構，其中大尺度渦團更多地受到宏觀整體流動環境的影響，而最小尺度渦團則在Kolmogorov尺度被耗散掉。各種尺度渦團通過經歷生成、發展、破碎和再生等過程，對瞬態流場施加影響。眾所周知，大尺度渦團往往攜帶著大部分的流場湍動能，這些渦團又可被稱之為擬序結構，它們在湍動能的產生和輸運過程中產生關鍵性的作用。然而到目前為止，研究者們還沒有對擬序結構給出明確的定義，只是將其描述為在時間性上具有準周期屬性，在空間上具有一定形態的流體組織結構。

近來，先進的光學診斷技術，如粒子圖形測速技術，先進的數值模擬技術，如大渦模擬，均得到快速發展，并成為研究湍流擬序結構的強有力工具。例如，可以通過使用這些工具記錄和再現瞬態流場信息，并形成完整的流場數據庫，為下一步的湍流場擬序結構特性研究提供數據支持。為實現從湍流背景中有效地識別和提取擬序結構，非線性數學方法的使用成了必要環節。

Lumley將本征正交分解（proper orthogonal decomposition，POD）引入到湍流研究領域，為人們提供了一種有效的數學分析手段和思路［1］。該方法可以將無窮維的非線性系統進行降維近似，對湍流場而言，POD可將瞬態速度場表示為一組POD模態的線性組合，模態反映著原瞬態流場空間內不同結構信息，并且相互之間線性無關，線性組合中各個模態對應的系數則反映著流場在時間演變上的信息。該方法的引入，極大地促進了湍流研究的發展。例如，POD方法可有效區別和分離不同的含能渦團結構，這為研究擬序結構提供了有效的手段。近來一些研究者應用該方法研究了發動機缸內流場，例如分離和重構了缸內矢量場（速度場）和標量場（溫度場、濃度場）。Raposo使用PIV手段測量了缸內流場，然后使用POD方法對測量數據加以處理分析［2］。Cosadia采用POD方法分析了缸內流場循環變動的特性［3］。Fogleman則使用POD方法研究了內滾流場破碎過程中湍流動態特性［4］。Haworth使用POD方法對一臺簡化的發動機缸內流場大渦模擬數據進行處理，分別研究了滾流和渦流的循環變動情況［5］。陳豪對實驗測量的200個循環流場數據進行了POD分析，針對所選數據有無進行相平均操作以及不同周期集合的選擇對POD分析結果產生的影響展開了討論［6］。秦文瑾提出POD 4分解方法，將瞬態湍流場分解為平均流場、擬序流場、過渡流場和湍流流場，并研究了4個分流場的循環變動情況［7］。李衛分別采用了相依賴POD方法和相不變POD方法研究了發動機缸內流場特性［8］。

本文中在前人研究的基礎上，嘗試將POD方法和Q準則方法進行結合，以用于發動機缸內湍流場擬序結構的研究中。通過對大渦模擬計算得到的缸內瞬態流場數據庫進行處理，來獲得缸內三維流場擬序結構特性，進而豐富人們對發動機缸內湍流場特性的認識。

1 本征正交分解

本征正交分解（POD）方法可以將瞬態流場分解為一組與空間信息相關的模態和一組反映時間信息的系數之間的線性組合：

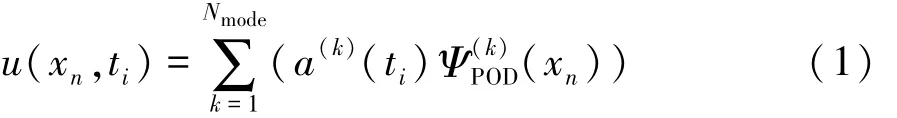
式中：ΨPOD（xn）為 POD模態；a（t）為 POD模態對應的時間系數。每個POD模態之間相互正交，原瞬態流場經POD分解后，大部分流場能量可被少數低階模態捕獲，從而為提取大尺度含能渦團成為可能，但對于空間采樣點較多的流場應用問題而言，經典POD方法計算成本較高。Sirovich提出的“快照”POD方法里［9］，速度場相關張量計算沒有采用空間采樣點數據的內積，而是采用不同時間采樣點數據內積得到，進而有效地提高了經典POD方法的計算效率。速度相關張量計算如下：

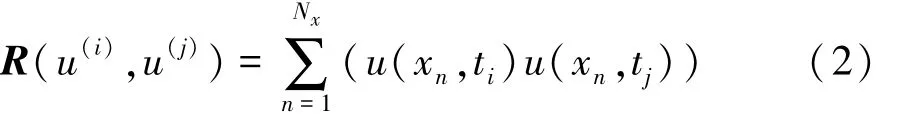
式中：Nx為空間采樣點數目；下標i和j分別代表不同采樣時刻。POD模態可通過將速度相關張量的特征向量與原始瞬態流場的內積獲得，如下式所示：

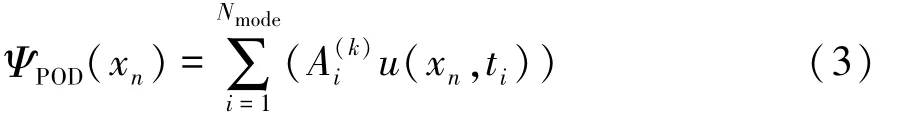
式中矩陣A由速度相關張量R的特征向量構成。

每個POD模態均與速度相關張量的特征值和特征向量一一對應，且每個POD模態捕獲的流場能量大小等于其對應的特征值幅值大小的一半。通過分析特征值幅值分布情況，即可獲得各POD模態所捕獲的瞬態流場能量分布特性。這樣，通過使用POD方法，不僅可以獲得瞬態湍流場不同尺度渦團空間結構特征，還能夠分析其能量分布特點。另外通過對POD時間系數的分析還能夠獲得其他流場信息，如循環變動的信息等。

2 數值計算介紹

大渦模擬方法采用空間過濾手段將瞬態流場信息分解為大尺度量和小尺度量，即亞網格尺度量。流場大尺度量可以直接通過數值模擬獲得，小尺度量則需要模型化來求解。采用較精細的網格，大渦模擬方法可以獲得比雷諾平均方法更加精確的模擬結果。對于流場分析而言，采用大渦模擬將有利于獲得更多流場細節。對于大渦模擬方法，亞網格應力可以通過幾種途徑獲得，例如通過采用代數方式建模，或通過采用輸運方程方式建模。本文中采用動態結構模型來求解亞網格應力。該模型沒有采用各向同性渦黏假設，即求解過程不涉及亞網格渦黏系數的求解，模型中亞網格應力被表示為亞網格湍動能和對應的系數張量的函數。該模型詳細信息可見文獻［10］。

為研究缸內流場擬序結構特性，對一臺四氣門單缸光學發動機進行了大渦模擬，完成了連續100個周期的冷態流場計算。幾何建模、計算初始條件和邊界條件均與實驗保持一致，實驗詳見文獻［11］，發動機參數見表1。計算采用有限體積法，對流項2階中心差分格式，變時間步長，最小網格精度為0.5 mm，真實氣體Redlich-Kwong狀態方程，標準壁面函數，并通過PISO算法求解該非穩態問題。在本文的表述中，0°CA規定為進氣沖程上止點時刻。

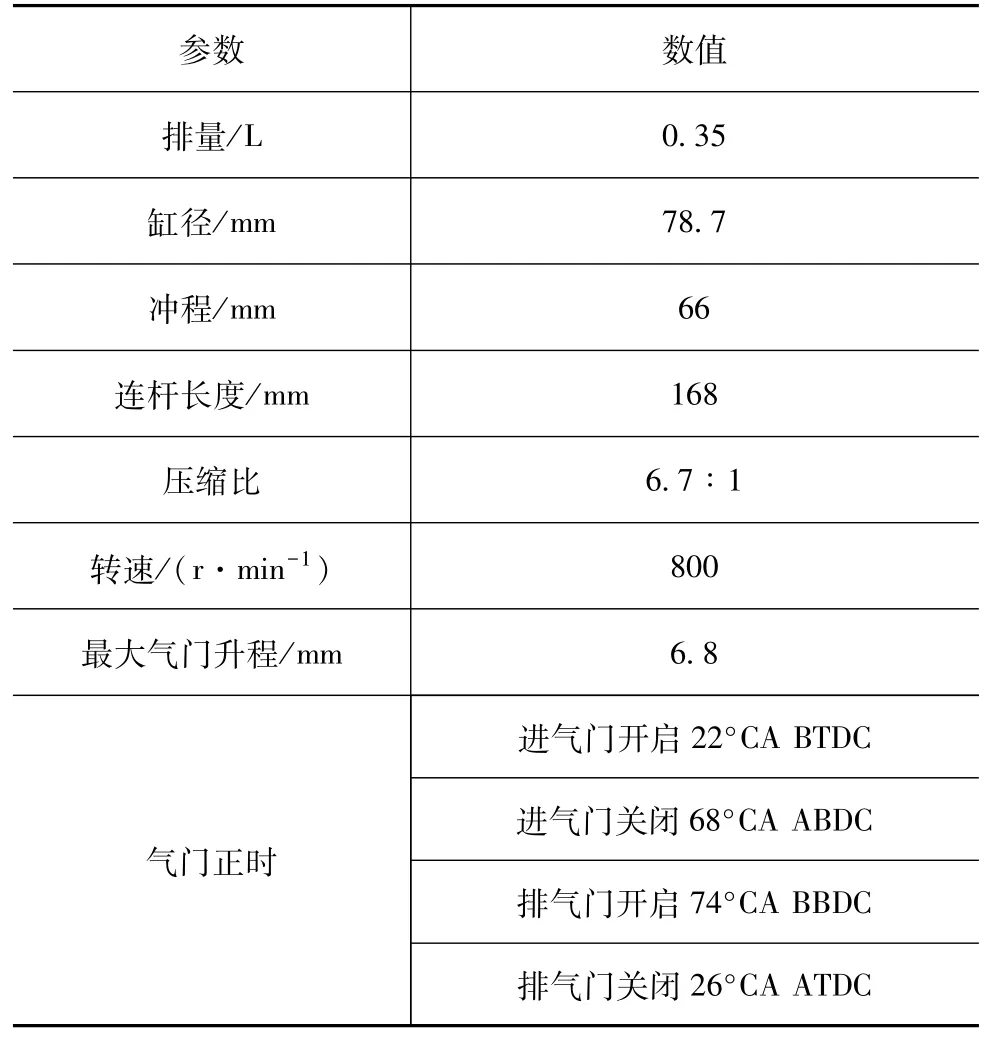
表1 發動機參數

3 結果與討論

在后臺階流或近壁面等基礎湍流流動模擬環節中，大渦模擬方法常常伴隨著采用高精度網格和高階離散格式，以便降低模型誤差和數值耗散誤差對模擬結果帶來的影響，特別是對微觀小尺度隨機湍流脈動的影響。Pope指出由高質量的大渦模擬所獲得的可解尺度湍動能應達到90%以上［12］，此時的大渦模擬可稱為“科學大渦模擬”。然而高精度的網格和數值離散格式對工程應用，特別是內燃機這種復雜幾何動邊界條件以及各項異性高瞬態多循環工作流場而言，并不實用。為了平衡計算效率和計算精度，計算常常采用低精度網格和低階離散格式，此時的大渦模擬又可被稱為“工程大渦模擬”［13］。故在本研究的大渦模擬計算環節，采用了較為稀疏的網格精度（最小網格尺寸為0.5 mm）和低階數值離散格式（2階中心差分格式）。

首先對大渦模擬計算得到的缸內垂直對稱平面滾流場與PIV測量結果進行了對比，由于缸內流場存在循環變動現象，單獨對比瞬態流場沒有實際意義，故首先將模擬和測量各自得到的100個連續流場進行相平均操作，然后進行比對，結果如圖1和圖2所示，線框表示PIV測量窗口范圍。通過觀察可以發現，在早期進氣沖程階段，進氣射流強烈，其主導著缸內整體流動形態，伴隨著活塞的下行，進氣射流強度持續下降，缸內整體流動形態也從進氣射流演化為大尺度滾流，該大尺度流動特征一直延續到壓縮沖程階段。模擬結果和實驗結果對比良好，說明本文中采用的動態結構大渦模擬模型可比較真實地再現發動機缸內流場。由于缸內流場是三維高度非定常湍流場，其中既包含著大尺度渦團運動，還包含著隨機分布的小尺度渦團運動，故二維流場不能全面反映發動機缸內流場信息，特別是對于擬序結構的特征信息。故以下工作將針對三維模擬結果展開，以期獲得較為全面合理的缸內流場特征。

本文中采用Q準則完成缸內渦團結構識別工作。Q準則基于速度梯度張量不變量原則，標量Q的定義如下：

圖1 大渦模擬計算得到的缸內對稱面滾流場

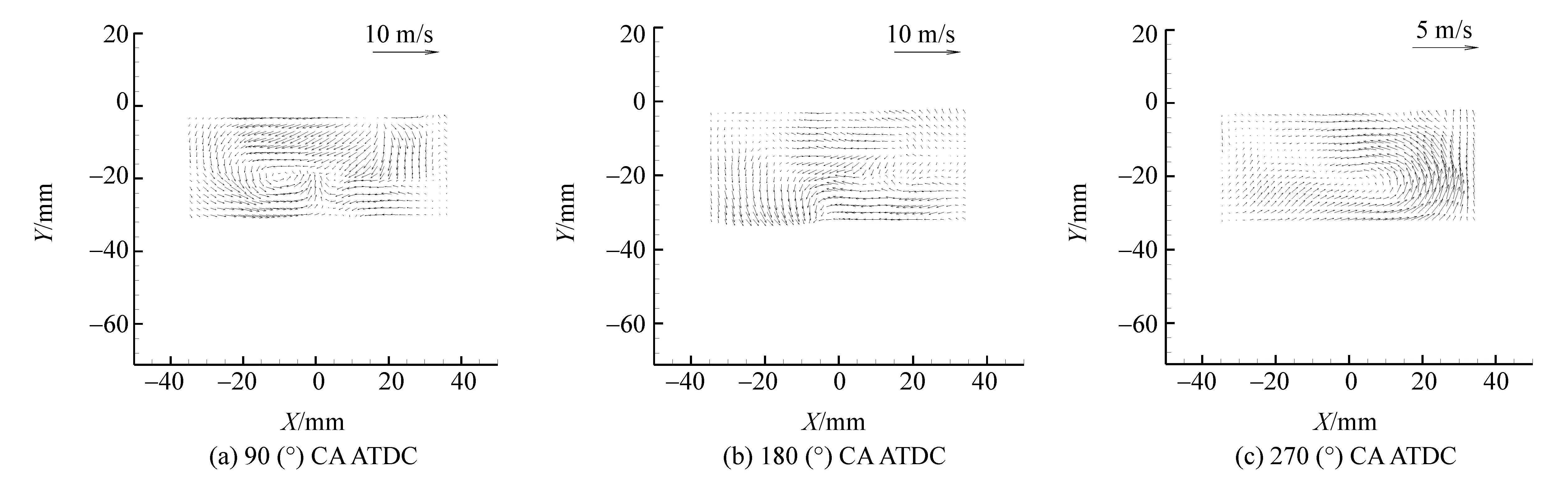
圖2 PIV測量得到的缸內對稱面滾流場

式中：Ωij為速度梯度張量非對稱部分；Sij為速度梯度張量對稱部分。它們分別代表著旋轉率張量和非旋轉應變率張量。當流場某處存在強烈渦團運動，該處的旋轉率張量幅值將明顯大于非旋轉應變率張量幅值，即該處的標量Q值為正，且數值較大。據此，可根據標量Q值大小來顯示流場渦團強度，且其等值面可以很好地展現渦團結構空間分布情況，故特別有利于識別大尺度擬序結構。

圖3和圖4展示了采用Q準則識別的缸內瞬態流場渦團結構和瞬態流場流線分布情況。在進氣沖程階段，通過兩個進氣門產生的進氣射流相互干涉，然后產生較為復雜的滾流運動。進入氣缸的高速氣流和缸內原有氣體之間形成強烈的相向剪切運動，進而促進大尺度渦團的產生。另外高速氣流和壁面的相互作用也促進了大尺度渦團的產生。較小尺度的渦團則主要產生并分布在缸內中心區域。在進氣沖程后期階段，缸內渦團運動強度顯著下降，大尺度渦團會被拉伸至破碎，進而產生數量眾多的小渦團，此時流場各項異性程度減弱。在壓縮沖程階段，大尺度渦團持續變形和破碎，進而促進小尺度渦團不斷產生，此時流場整體渦團強度變的更弱，且更加均質化。通過以上過程，可以發現缸內流場演變經歷從進氣沖程強烈的各項異性，經過流場渦團破碎強度衰減，在壓縮沖程階段逐漸趨于各向同性。

本文中將POD方法對大渦模擬缸內流場數據進行加工，以期獲得更加詳細的流場擬序結構信息。首先考察了POD方法的收斂特性。將不同數量“快照”流場（即不同周期流場）分別進行POD運算，若同樣階次的兩組POD模態保持一致，則說明所選用的“快照”數量實現了收斂目的，再額外增加“快照”數量，對于理解流場特性并不會增加額外的信息。文中采用相關性系數和誤差范式兩個參數來量化兩組不同模態空間信息差異性。在POD模態達到收斂的過程中，相關性系數應逐漸接近1，而誤差范式則應逐漸接近0。

本文中安排了9組由不同“快照”數量構成的數據集合，9組集合分別包含20，30，…，100個“快照”數量，然后對每組集合分別進行POD運算。5個POD模態（模態 1，模態 3，模態 5，模態 7，模態 9）進行了收斂性參數計算，結果如圖5所示。在所有POD模態里，模態1代表著流場平均流動狀態，并攜帶著流場絕大部分能量，故該模態在較早階段就實現了收斂。對于其他高階模態（模態3-模態9）收斂速度則越來越慢。這表明對于獲取高階模態刻畫的流場信息，需要使用更多數量的“快照”。通過觀察相關性系數和誤差范式的收斂趨勢，可以發現在本次研究中使用90個“快照”即可實現各組模態收斂，即不必使用全部100個數量的“快照”。

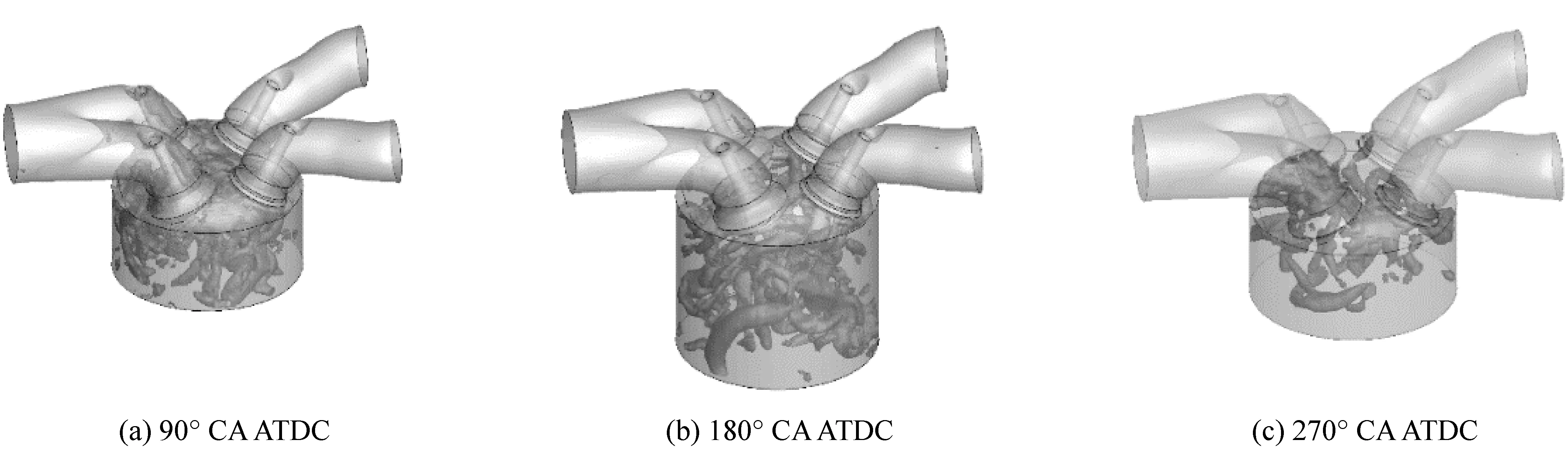
圖3 缸內擬序結構

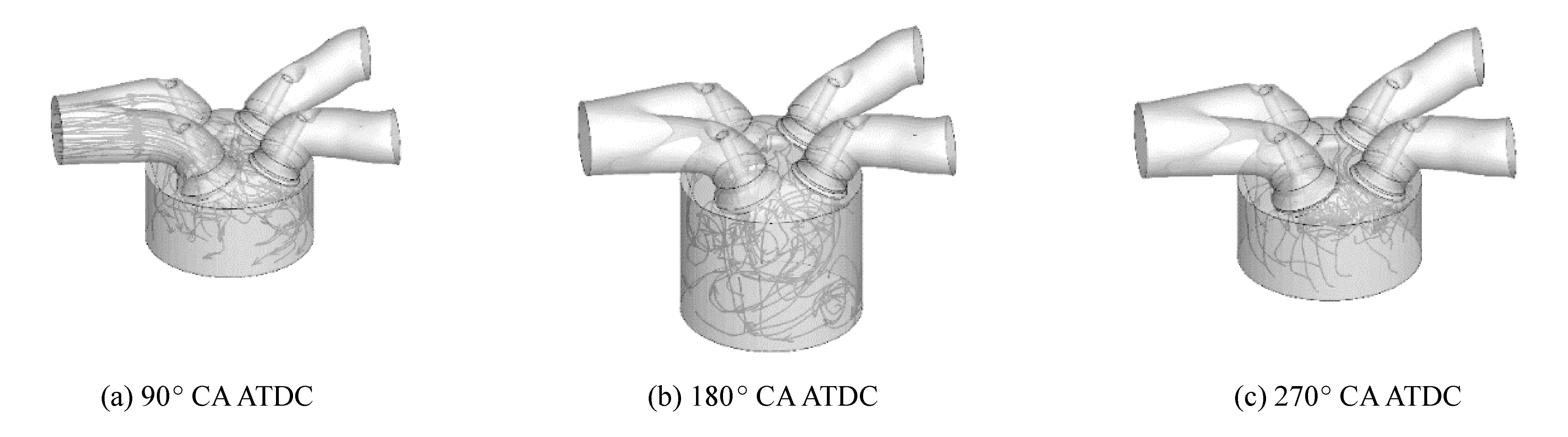
圖4 缸內速度場流線

圖5 POD模態收斂情況

除了考察空間POD模態收斂情況，還可以考察POD模態含能收斂情況。在POD方法中，特征值大小可以反映POD模態含能分布情況。按照特征值幅值從大到小進行排列，所對應的模態1則攜帶著流場絕大部分能量，而其他模態含能數量則逐漸遞減。本文中計算了不同數量“快照”流場進行POD運算后的特征值序列，并加以無量綱化。單獨模態含能情況以及多個連續模態累計能量情況如圖6所示。可以發現，模態1攜帶的能量最先達到收斂，其他高階模態含能收斂速度則逐漸變慢，再次說明使用更多數量的“快照”有利于高階模態刻畫的流場信息獲取。

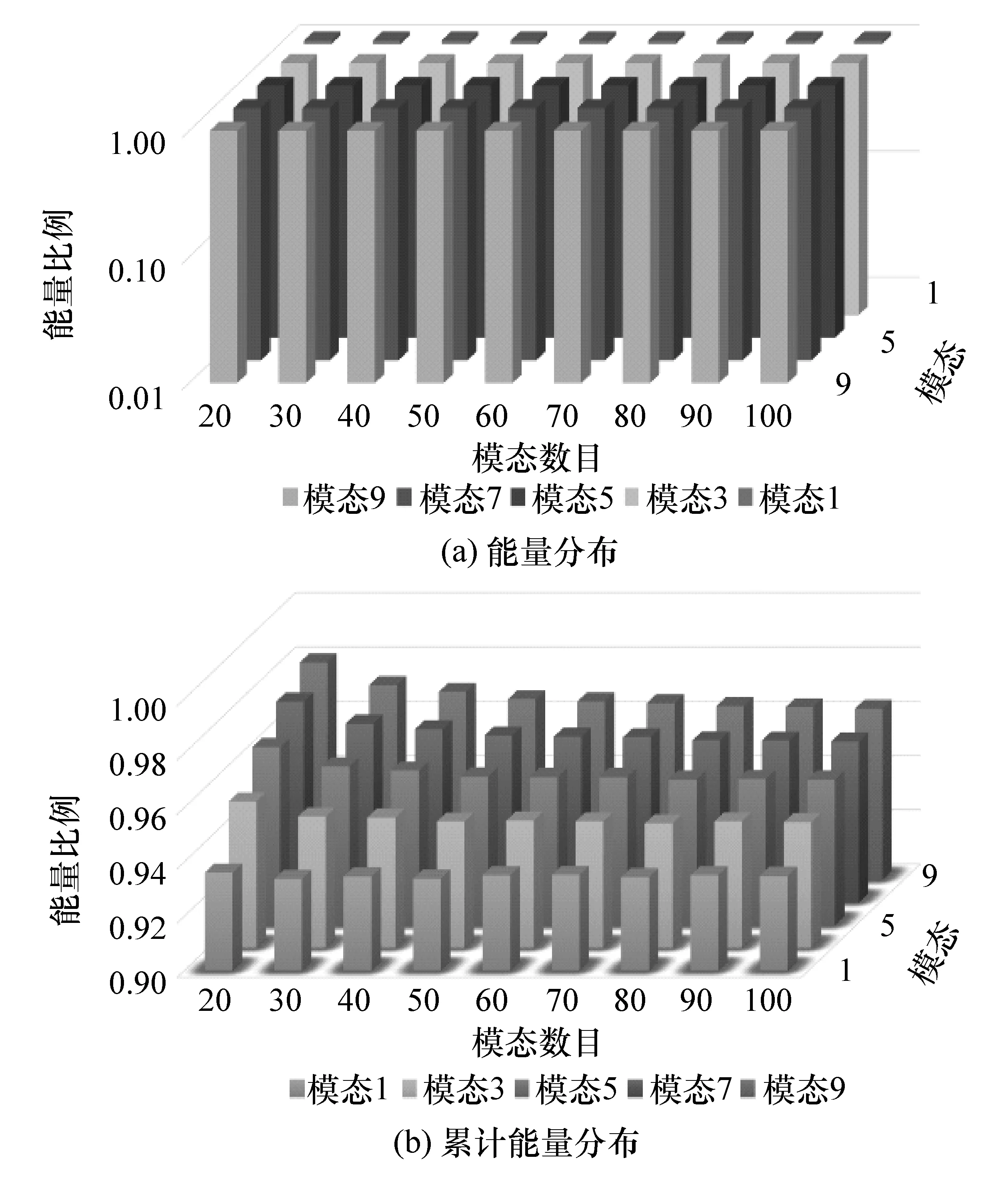
圖6 POD模態能量收斂情況

流場經過POD分解后，不同的含能流場結構可實現有效分離，即低階模態反映大尺度含能高的流場結構，如整體流動或局部擬序結構等，而高階模態則主要反映空間隨機分布的小尺度渦團結構。由于Q準則特別適用于三維流場渦團結構的識別，故本研究采用Q準則對缸內三維流場POD分解后得到的不同模態進行渦團識別，從而可以比較直觀地刻畫不同POD模態所反映的流場含能結構三維空間分布。圖7～圖9是使用Q準則識別的6個不同POD模態（模態1，模態2，模態3，模態4，模態50，模態90）內渦團空間分布情況。為方便不同沖程階段內渦團空間分布對比，在3個不同曲軸轉角時刻，標量Q分別取值為2，0.3和0.2（數值越大表明渦團強度越高）。進氣沖程階段強烈的進氣射流主導著缸內滾流運動，而高速氣體相向剪切運動則促進小渦團的隨機產生。通過觀察，可以發現此時模態1中的標量Q主要刻畫了進氣射流運動情況下的渦團形態。這些渦團主要分布在進氣門氣道附近處，并攜帶著流場絕大部分能量，在之后的流場演變過程中，這些渦團將會變形并輸運到缸內，逐漸演變成大尺度擬序結構。模態2中的標量Q刻畫了缸內流場整體滾流運動情況下的渦團形態，這部分渦團會伴隨著滾流運動實現空間分布的演變。模態3、模態4中的標量Q刻畫了一些較大尺度的擬序結構，其主要分布在氣門下方缸體中央區域，這部分渦團結構對缸內流場湍動能的維持起到了重要的作用。正是由于通過擬序結構的形成、變形和破裂，缸內流場實現了能量級聯。而其他高階模態下的標量Q則主要刻畫小尺度隨機渦團結構，從圖中也可以發現，模態越高其刻畫的小尺度渦團越具有隨機性，其空間結構分布越來越均勻，即呈現各項同性的特點，這部分渦團在湍流黏性的作用下被逐漸耗散掉。在進氣沖程后期，進氣射流強度降低，缸內流場整體流動強度同步減弱。越來越多的大尺度擬序結構被拉伸并破碎成更多較小尺度渦團，流場能量則從大尺度含能渦團傳遞到小尺度渦團內。通過觀察，可以發現，此時在POD模態1中的標量Q不再主要刻畫進氣射流中的渦團結構，而是刻畫整體滾流運動情況下的渦團形態，與早期的整體滾流運動下的渦團形態相比，此時這部分渦團強度和數量呈現明顯降低。模態2～模態4中的標量Q則刻畫的是較大尺度擬序結構，同樣，其他高階模態中的Q則依然刻畫小尺度渦團。在壓縮沖程階段，進氣射流影響消失，流場整體運動形態削弱，能量級聯現象依然在渦團不斷破裂的過程中發生。大量隨機小渦團不斷產生，并分布在缸內整個空間，流場逐漸趨于各向同性。此時模態1中的標量Q依然刻畫整體滾流運動中的渦團結構，模態2中的標量Q刻畫隨機分布的擬序結構，其他高階模態中的標量Q刻畫尺度逐漸減小的渦團結構。通過以上分析可知，采用Q準則對本征正交分解后的POD模態進行加工，可以很好地識別不同含能結構內的渦團，以便研究者觀察和分析這些渦團的空間形態分布和演變情況。

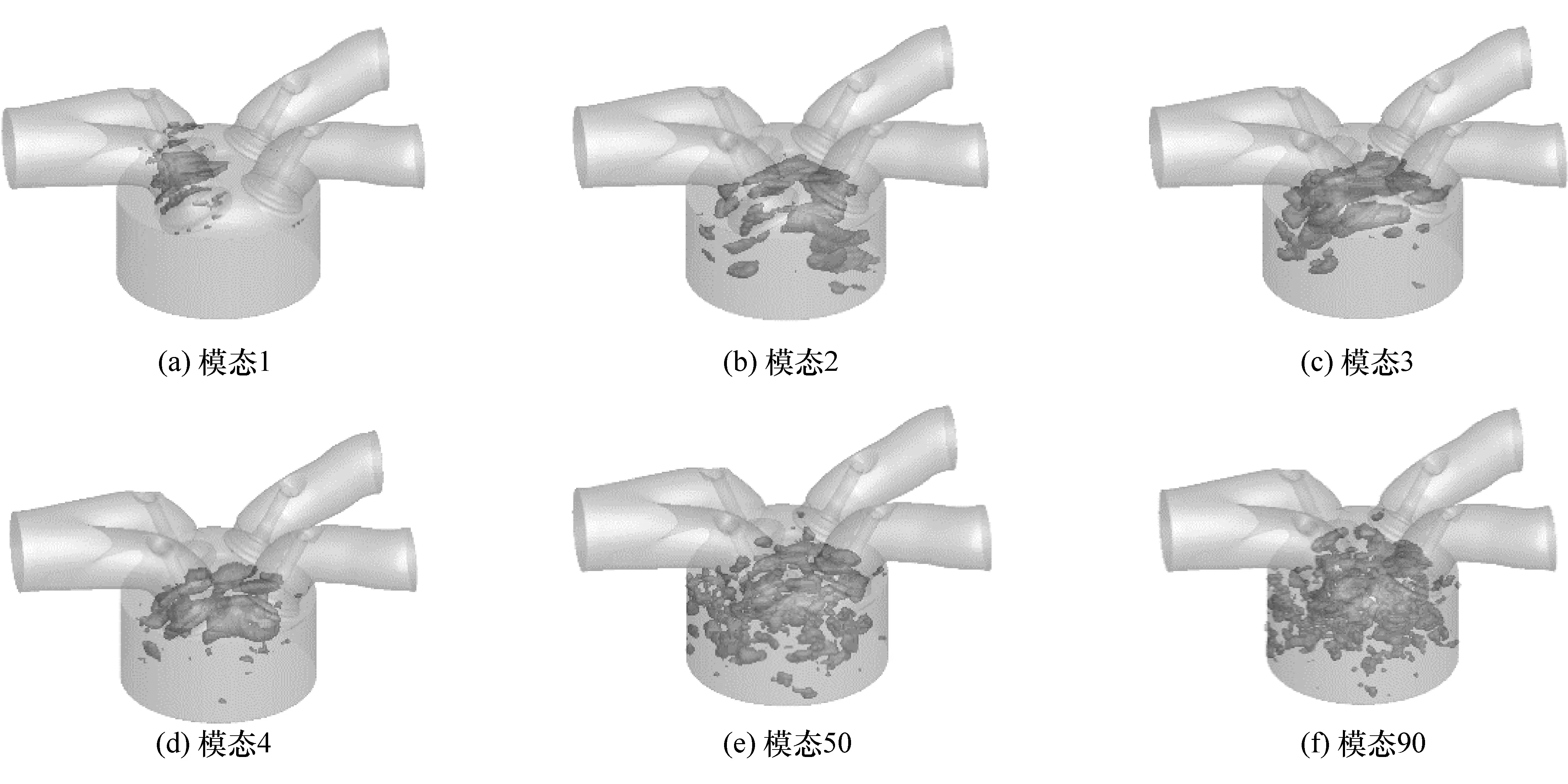
圖 7 90°CA ATDC（Q=2）

圖 8 180°CA ATDC（Q=0.3）

圖 9 270°CA ATDC（Q=0.2）

4 結論

本文中主要研究缸內流場擬序結構特性，通過對一臺四氣門單缸光學發動機進行了大渦模擬冷態流場計算，計算結果通過PIV實驗驗證。采用Q準則方法來識別缸內包括擬序結構在內的不同尺度流場渦團結構。隨后采用本征正交分解方法對模擬得到的缸內流場數據庫進行深加工，主要結論如下。

（1）進氣沖程階段，進氣射流強烈，其主導著缸內整體流動形態，缸內滾流運動形態形成，流場速度可達10 m/s。高速射流氣體與缸內原有氣體相向剪切運動產生較大尺度渦團。在壓縮沖程階段，渦團強度減弱，大尺度不斷破碎成小尺度渦團，流場速度下降到5 m/s以下。能量級聯現象在該過程中發生，流場逐漸趨于各向同性。

（2）對于POD操作，雖然較多數量的流場“快照”有利于分析高階POD模態反映的流場信息，但“快照”數量達到一定程度后，額外增加流場“快照”并不能有效地提供更多流場信息，如本研究中采用90個“快照”即可很好地描述所有100個“快照”全部信息。

（3）POD模態和Q準則的結合使用，可以很好地識別和刻畫不同含能尺度下的缸內流場結構，低階模態（模態1-模態4）主要識別整體流動狀態和大尺度擬序結構，而高階模態則（模態50-模態90）主要識別缸內隨機分布的小尺度渦團結構。