基于LabVIEW的頻域抽樣定理實驗

栗學麗

（山東大學 微電子學院，山東 濟南 250101）

時域抽樣定理和頻域抽樣定理是數字信號處理課程中的兩大基本定理。相比于時域抽樣定理的研究[1]，頻域抽樣定理的研究相對較少[2]，在教科書中只有簡單提及且不易學生理解[3]。文獻[4]和文獻[5]分別給出對一個序列抽樣32點和抽樣16點、32點的編程驗證示例，這些都是特殊點值；文獻[6]的編程可以任意變化抽樣點數，但只適用于抽樣點數大于序列長度的情況。

LabVIEW 采用圖形化編程，具備強大的信號處理、數據分析等功能，方便用戶建立自己的虛擬儀器，使編程和使用過程都生動有趣[1]。目前基于LabVIEW的虛擬實驗開發被廣泛應用于工業、科研和教學等領域[7]。本文通過直接抽樣法和離散傅里葉變換（DFT）法兩種編程方法，實現基于 LabVIEW 的虛擬仿真實驗來驗證頻域抽樣定理，幫助學生避免編程誤區、更好地理解和運用頻域抽樣定理。

1 頻域抽樣定理

離散信號的頻譜仍然為連續信號，不便于計算機處理。對其進行頻域抽樣，可得到離散頻譜，這對應于DFT過程。這個抽樣點數必須滿足一定的條件，才能從離散頻譜的離散傅里葉逆變換（IDFT）中恢復出原始信號。頻域抽樣定理就是研究抽樣點數所滿足的條件。

如果序列x(n)的長度為M點，若對其頻譜在上作等間隔抽樣，共有N點（抽樣點不包括ω=2π），得到只當抽樣點數滿足N≥M時，才能由X~(k)恢復出x(n)，即否則將產生時域的混疊失真，不能由不失真地恢復出原序列x(n)。這就是頻域抽樣定理，理論證明見文獻[8]。頻域抽樣定理是DFT和IDFT的理論基礎，是利用DFT計算離散信號頻譜的理論依據。頻域抽樣定理以及由它推導的內插公式可提供一種有用的濾波器結構和濾波器設計途徑[9]。此外，它還應用于雷達信號的目標識別[10]和通信上的頻分復用[11]。由此可見，頻域抽樣定理非常重要。本文基于LabVIEW設計了頻域抽樣定理虛擬仿真實驗。

2 頻域抽樣定理實驗界面設計

根據頻域抽樣定理，需對任意一個離散信號（序列）求得其頻譜值再進行抽樣，故需先設計一個任意離散信號。由傅里葉變換可知，若信號滿足絕對可和，則這個信號可表示為正弦信號的線性組合。因此，正弦信號是基本信號，可選幅值、頻率、相位、信號長度可調節的正弦信號作為基本測試信號，也可以由用戶自行輸入信號表達式作為測試信號。故在頻域抽樣定理實驗界面的左側設計可調測試信號源，分別為正弦信號和用戶的公式輸入信號，使信號源不再是單一的信號源。

為了更好地反映信號的時域和頻域關系，可以用波形圖直觀表示信號的時域、頻域值，幫助學生理解頻域抽樣定理的過程及其結果。還應有一個可調的抽樣點數按鈕，從而實現頻域抽樣定理在不同抽樣點數下的過程變化。故在實驗界面的右側設計圖形顯示區，分別顯示原始信號時域圖、原始信號幅度譜、頻域抽樣后的幅度譜和恢復信號時域圖。各圖之間用箭頭表示計算過程的流向，使數據顯示直觀和便于比較。用戶可以通過改變頻域抽樣點數按鈕，觀察不同抽樣點數下的仿真實驗圖形和驗證頻域抽樣定理。

通過 LabVIEW 軟件將所需顯示的控件拖放到前面板，可以很方便地設計出具有虛擬儀器外觀的交互式用戶界面。這些控件的圖標自動出現在 LabVIEW的程序框圖上，就可通過連線實現編程。

3 頻域抽樣定理實驗編程實現及驗證

在 LabVIEW 的程序框圖上進行編程，信號源部分由子程序signal_new.vi實現，其程序框圖如圖1所示。由于正弦信號的生成比較簡單，故不再詳述。用戶通過公式輸入信號，主要是通過解析公式節點（Parse Formula Node.vi）和已解析公式節點求值（Eval Parsed Formula Node.vi）等編程得到。

頻域抽樣定理的實現，關鍵是信號頻譜各抽樣點上頻域值的獲得。下面通過直接抽樣法和DFT法分別實現頻域抽樣定理。

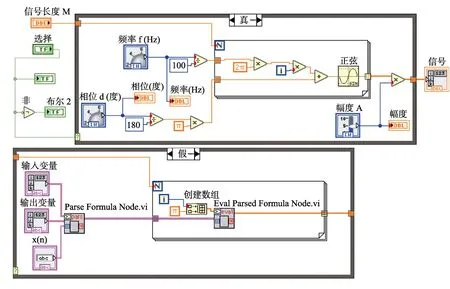
圖1 信號源子程序signal_new.vi程序框圖

3.1 直接抽樣法

按照頻域抽樣定理，應先對長度為M點的時域信號x(n)進行離散時間傅里葉變換（Discrete-Time Fourier Transform，DTFT），得到其連續的頻譜值再在其上等間隔抽樣得到N個抽樣點上的頻譜值，對這些離散頻譜抽樣值做IDFT，得到恢復信號比較x(n)與x′(n)的差別。

直接抽樣法程序框圖如圖2所示。由于當P點值遠遠大于信號長度M時，由DTFT得到的頻譜可通過P點的DFT（FFT.vi）近似實現，這里P取大于M的100倍且是抽樣點數N的整數倍的最小值，然后用降采樣（單次）函數（Decimate (single shot).vi）實現等間隔抽樣為間隔值），得到頻譜上的各抽樣點值，進而用 IDFT（Inverse FFT.vi）得到恢復信號x′(n)。通過改變頻域抽樣點數，觀察x′(n)并與x(n)比較，以驗證頻域抽樣定理。

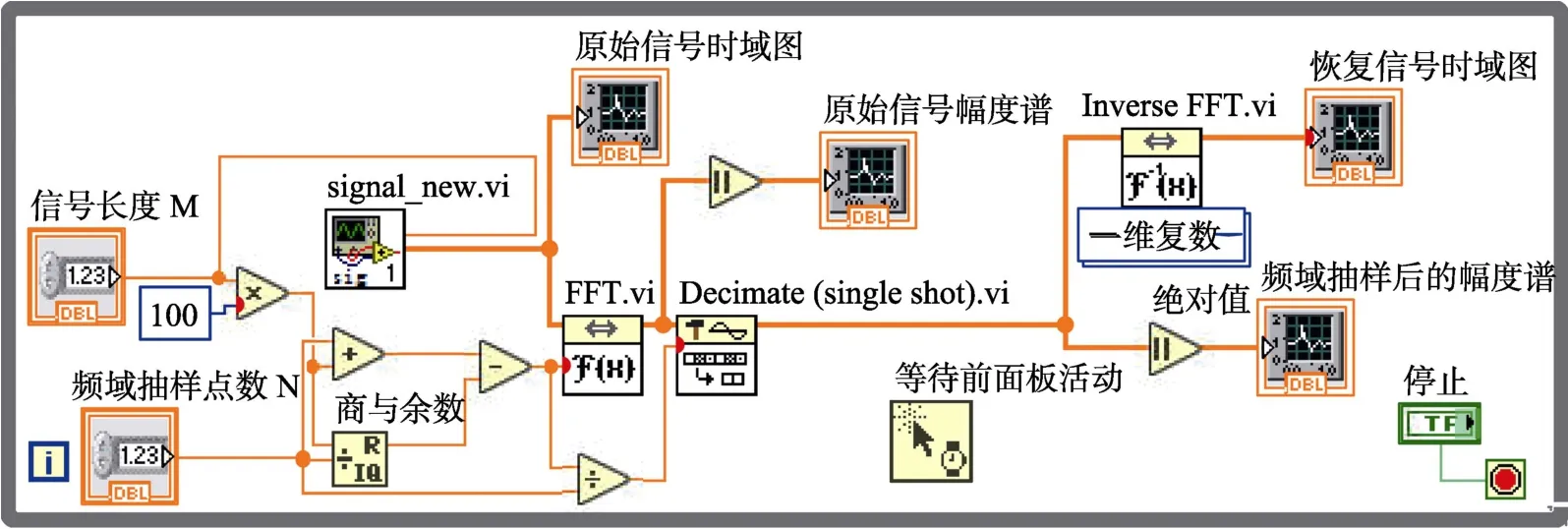
圖2 直接抽樣法程序框圖

這里，P值不能像文獻[4-5]取1024定值，因為一個定值不能保證對所有的N值都能有整數的等間隔值，這也是許多做實驗編程的學生常犯的錯誤。雖然程序并不報錯，但仔細比較就會發現程序運行結果并不是對所有的N都正確。本程序中將P設定為大于M的 100倍，保證了P?M，可由 DFT值得到 DTFT值。且P為N的倍數，為一個隨N變化的值，又保證了T=P/N為整數，能實現等間隔抽樣。這樣，對不同的N值都能正確驗證頻域抽樣定理。

通過這樣編程實驗，可以使學生更深刻地理解DTFT與DFT的關系，理解信號的頻譜、等間隔抽樣和頻域抽樣定理的含義。

3.2 DFT法

頻域抽樣值是通過對時域信號進行N點的 DFT得到的，再對它進行N點的IDFT得到恢復信號。有些學生參考文獻[6]直接對長度為M點的x(n)做N點的DFT，其值作為N點等間隔頻譜抽樣值。為說明該方法是否對所有的N值都成立，分別對N≥M和N＜M兩種情況進行推導。

已知

（1）N≥M，將x(n)補零到N點，

（2）N＜M，設

可知，當N≥M時，用x(n)的N點DFT可以得到N點頻域抽樣值；當N＜M時，N點頻域抽樣值是對信號做N點DFT得到。

由此可見，當N≥M時，用x(n)的N點DFT得到N點頻域抽樣值是正確的；但是當N＜M時，就不能這樣做，而是應先計算出然后對它求N點的DFT值，才是正確的頻域抽樣值。所以正確的編程應按照上述原理。DFT法程序框圖如圖3所示，用分支結構分別編寫N≥M和N＜M的情況。通過重排數組維數、二維數組轉置、數組元素相加等函數編程實現。

3.3 頻域抽樣定理驗證

圖 4給出N＜M時用戶公式輸入信號用 DFT法得到結果的一個示例。對每種情況用直接抽樣法和DFT法得到的結果是相同的，兩種求解方法思路不同，但它們的實質是一致的，只是DFT法編程稍微復雜。通過調節不同的信號源和不同頻域抽樣點數，可以驗證頻域抽樣定理的正確性。當N≥M時，頻域抽樣值恢復出的信號x′(n)比原信號x(n)多N-M個零點；當N＜M時，x′(n)比x(n)長度短，發生了時域混疊失真。學生通過調節不同的信號源和不同的頻域抽樣點數，可直觀地觀察到原信號、信號頻譜、頻譜抽樣值、恢復信號的圖形，深刻理解頻域抽樣定理。實驗編程過程學生也會將所學的知識融會貫通，將理論應用到實踐，真正領會到理論的意義及作用[12]。

圖3 DFT法程序框圖

圖4 N＜M時一個示例界面

4 結語

利用 LabVIEW 設計并實現了頻域抽樣定理仿真實驗，它具有交互性好、通用性強、方便比較、驗證結果正確等特點，有利于學生深入理解和應用頻域抽樣定理。通過實驗案例可見，理論推證是實驗編程的基礎，基于 LabVIEW 實現的參數可調的虛擬仿真實驗又可直觀地驗證理論，調動學生探索的興趣。理論和實驗相輔相成，能更好地提高教學質量。