混合多穩態隨機共振的故障信號檢測

張 剛， 李紅威

(1. 重慶郵電大學 通信與信息工程學院,重慶 400065；2. 重慶郵電大學 信號與信息處理重慶市重點實驗室,重慶 400065)

強噪聲背景下的微弱信號檢測技術一直是信號檢測與處理領域的研究熱點，它在機械設備狀態監測與故障診斷、應急救援和地震預測等領域應用廣泛。微弱信號檢測的本質為提高有用信號信噪比，因此檢測技術主要集中為抑制含噪信號中的噪聲提升信噪比，如濾波法、取樣積分法、小波降噪、經驗模態分解和變分模態分解[1]。但該類方法檢測粒度大且易損壞有用信號，造成檢測效果欠佳；而隨機共振在檢測微弱信號時利用噪聲能量不損害待測信號成為目前研究的熱點。

隨機共振是Benzi等于1981年研究古氣象變化時提出的，隨后在物理、生物、電子等領域均得到證實[2]。應用到微弱信號檢測中是將含噪信號通過非線性系統使周期驅動力和噪聲驅動輸出出現周期性的變化從而可將噪聲的一部分能量轉移給待測信號。隨機共振產生的必要條件為勢函數、噪聲和信號的協同作用，大量學者圍繞這三方面隨機共振因素進行了深入研究，以一階Langevin方程為基礎的過阻尼隨機共振模型分別有Woods-Saxon單穩態系統模型[3]、混合雙穩系統模型[4]、三穩態模型[5]、并行陣列系統模型[6]；二階方程較過阻尼具有近似濾波功能并且模型中含有可調的阻尼比增強了對噪聲的適應能力，因此關于二階方程的研究也在如火如荼的進行，比如基于逃逸率二階方程下的廣義調參隨機共振[7]、二階方程三穩態系統[8]。以上研究絕大數都是以理想化的高斯噪聲為背景，與實際的噪聲環境存在偏差，而α噪聲是具有顯著的拖尾特性和尖峰脈沖特性的非高斯噪聲，能夠更加接近于實際振動信號檢測應用場景，因此α噪聲作為背景噪聲受到越來越多的關注，其中有α穩定噪聲下時滯非對稱單穩系統隨機共振[9]、α噪聲驅動的非對稱雙穩隨機共振現象[10]、α噪聲背景下的脈沖幅度調制(Pulse Amplitude Modulation, PAM)信號檢測[11]。由于隨機共振受到絕熱近似理論的限制,因此在信號方面系統只能檢測低頻(f?1 Hz)信號,而在實際工程中其信號頻率遠遠大于1 Hz，極大的限制了隨機共振的應用發展,學者們通過不同的信號預處理方法打破傳統只能檢測小信號的桎梏,其中包括移頻變尺度隨機共振[12]、二次采樣的隨機共振技術[13]、頻率控制的自適應隨機共振[14]、信號頻譜重構的隨機共振[15]等等。以上研究使得隨機共振應用在實際工程信號處理中成為可能，其中最為典型是旋轉機械系統故障檢測，旋轉機械在交通工具、航空發動機、發電機等廣泛的工業應用中發揮著重要作用，其運行狀態的好壞直接影響生產生活安全，但是由于復雜機械設備中存在大量強噪聲使得軸承信號檢測變得尤為困難，因此旋轉機械的故障診斷問題極為突出。近年來涌現出大量研究:指數單穩隨機共振系統的軸承故障信號檢測[16]和變步長二階隨機共振系統的滾動軸承故障檢測[17]、隨機共振與經驗模態分解結合的滾動軸承故障檢測[18]等。目前為止，研究者發現Woods-Saxon模型具有平滑的底部，陡峭的勢壘壁，能夠保證粒子穩定運動使其達到較好輸出[19]，而三穩態模型在微弱信號檢測時有比其他穩態對噪聲利用率高的特點；因此本文將混合雙穩態隨機共振系統與Woods-Saxon模型相結合，提出混合三穩態隨機共振系統；然后利用自適應算法尋找混合型三穩隨機共振系統最優參數組合，對α噪聲背景下的仿真信號進行檢測，證明其優越性；最后為了更加充分的聚集目標頻率能量，將變分模態分解和混合三穩態隨機共振進行組合并應用于實際軸承故障信號檢測，仿真結果顯示系統檢測出的故障頻率與實際計算特征頻率相差無幾，進一步驗證了該系統的實用性，為該系統在實際工程的應用奠定了基礎。

1 系統模型

1.1 Woods-Saxon單穩態

Woods-Saxon為對稱的單穩態函數

(1)

式中：a為穩態壁陡峭程度；V為穩態深度；R為穩態寬度。由圖1可知：穩態的兩端收斂于x軸。由圖1(a)可知:固定V,R單獨調節a可以改變穩態壁的陡峭程度，并且隨著a的減小穩態勢阱壁逐漸變得陡峭。由圖1(b)可知：固定R，a單獨減小V，穩態深度減小，由圖1(c)可知:固定V，a，調節R，穩態的寬度隨著R的增大而增大并由其單獨表征。因此勢函數的形態由a,V,R聯合控制，系統參數間的耦合性不高，可有效控制勢函數的形態。

1.2 混合雙穩態模型

在混合雙穩態模型中勢函數Um(x)是非線性對稱雙勢阱，其勢函數為

(2)

圖2表示隨著穩態參數b的增大，穩態壁逐漸變得陡峭且勢壘高度減小，勢函數形狀由w型逐漸轉變為u型；因此可知參數b將影響混合雙穩態的穩態個數及穩態寬度，可有效控制混合型雙穩態涵蓋域及穩態間過渡。

圖1 勢函數隨不同參數的變化Fig.1 Potential function for different parameters

圖2 混合型雙穩勢函數隨b的變化Fig.2 Hybrid bistable potential function for different b

1.3 組合模型

基于以上兩種模型將Woods-Saxon單穩態模型與混合雙穩態模型相結合提出一種混合型三穩態模型，勢函數為

(3)

圖3是混合型三穩態的勢函數，其參考形態結構參數為(V,R,a,b)=(0.6,0.4,0.1,0.3)，由圖3可知該函數為軸對稱圖形，兩邊勢阱屬于混合雙穩態勢阱而中間勢阱屬于Woods-Saxon,從而可知該系統既保留了Woods-Saxon的特性又增添了三穩態的優點。

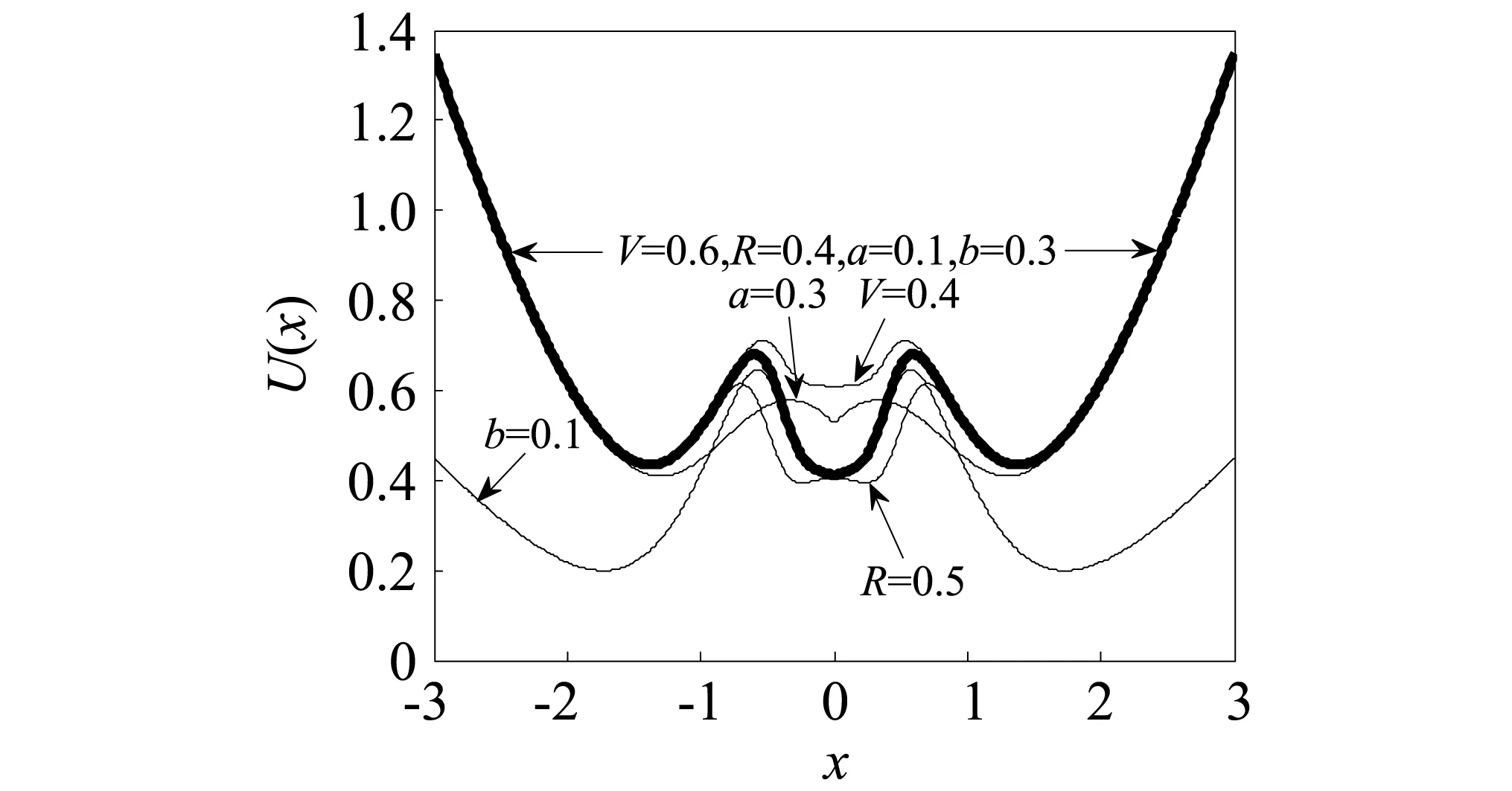
圖3 混合型三穩態勢函數Fig.3 Hybrid tri-stable potential function for different value

通過調節系統參數V可知影響中間穩態深淺，參數a影響中間穩態壁的陡峭程度，參數R影響中間穩態區域窄寬，參數b影響整體勢函數兩邊穩態壁的陡峭，由布朗粒子運動及勢函數形態關系可知：布朗粒子從單或雙勢阱躍遷變為三勢阱躍遷，極大的提高了噪聲的利用率，而由這些參數引起的勢阱與勢壘的改變也直接影響粒子的躍遷難易程度。

1.4 系統模型

隨機共振的三要素分別為：微弱驅動信號、噪聲和非線性系統，代入布朗粒子運動方程中可以理解為布朗粒子在外部周期驅動力下通過非線性系統在勢阱間的躍遷達到周期性，在不足以越過勢壘的情況下，通過協調噪聲的能量完成勢阱間的躍遷,因此二階三穩態布朗粒子運動方程為

(4)

其中傳統的隨機共振系統勢函數及勢阱力為[20]

(5)

而由式(3)可知混合三穩態勢阱力為

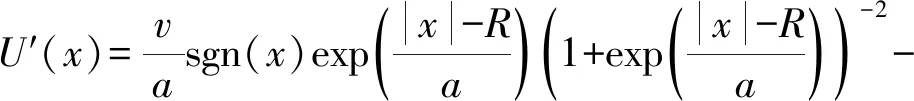
(6)

由隨機變量(x,y)的Fokker-Planck方程可知其概率密度函數

(7)

式中:k為阻尼比;s(t)為外部周期驅動力;ξ(t)為α噪聲，其特征函數表達式為

(8)

由式(8)可知α值決定該分布的拖尾特性和脈沖特性。拖尾特性和脈沖特性在α變化時呈現互反性，α值由小變大時拖尾特性由強變弱，脈沖特性由弱變強。β∈[-1,1]為對稱參數，確定分布的對稱性稱。參數σ∈[0,+∞)是尺度系數；μ∈(-∞,+∞)是位置參數，決定該分布的中心位置。由于α的特征指數越小，脈沖幅值就越大，振蕩粒子跳躍的距離很可能趨向無窮大，針對這個問題，經過大量仿真驗證對于混合三穩態數值仿真時對輸出截斷為5，雙穩態為2。

1.5 α噪聲的產生方法

α噪聲的隨機變量X通過Chambers-Mallows-Stuck方法產生[21]，當α≠1時

(9)

其中，

(10)

Dα,β,σ=σ[cos(arctan(βtan(πα/2)))]-1/α

(11)

當α=1時

(12)

式中：V為(-π/2,π/2)上的均勻分布；W為均值為1的指數分布，并且V和W相互獨立。

1.6 二階穩態方程的四階Runge-Kutta法

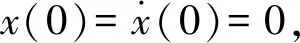
(13)

1.7 系統參數優化調節

隨機共振的產生依靠調節噪聲強度、系統參數使其產生協同作用來增強淹沒在噪聲中的有用信號，但是在此過程中需要判定系統是否產生了隨機共振，因此定量測度指標更加有助于實現和應用隨機共振現象目前性能指標主要包括信噪比、信噪比增益、互相關系數、駐留時間等，而隨機共振的主要特點就是將噪聲的能量轉化為有用信號的能量從而使有用信號實現非線性放大，最為直觀的性能指標就是判定系統對輸入信號進行非線性放大的程度。因此本文選取信噪比增益作為性能判定指標，其定義為輸出信號功率譜中信號頻率處的幅值與輸出背景噪聲之比同輸入信號功率譜中信號頻率處幅值與輸入背景噪聲之比的比值。該比值能較清晰的理解輸出相比輸入的受益程度，定義為

(14)

式中：snrout(f0)為輸出信噪比；snrin(f0)為輸入信噪比。由于實際應用場景中噪聲的復雜程度，外界噪聲源一定時其噪聲強度固定，因此通過調節噪聲強度實現隨機共振較困難，目前的研究主要集中在系統結構參數調節實現共振，由“2.3”節可知，中間勢阱主要依賴V，R，a控制，兩邊勢阱的調節主要影響因子為b，耦合性較低，本文選取自適應參數調節隨機共振，其具體步驟如下：

步驟1 初始化V，R，a及b,分別給定迭代步長和范圍；

步驟2 更新V，R，a,在b的給定范圍內搜索,比較信噪比增益,并記錄最大信噪比增益時V,R,a,b;

步驟3 判斷V,R,a是否超出搜索范圍,若未超出則轉到步驟2，若超出則停止更新轉到步驟4；

步驟4 分別在步驟2記錄的信噪比增益中調節k,找出并記錄每次調節過程中的最大信噪比增益；

步驟5 比較步驟4記錄的信噪比增益,找出最大的信噪比增益所在的V，R，a,b,k。

選取參數s(t)=0.8cos(0.2πt)，采樣頻率fs=5 Hz和采樣點數N=10 000，α噪聲參數：a=1.2，β=0和σ=1，μ=0，對于圖4(a)選取系統參數a=3，R=1和b=0.02，k=0.1，圖4(b)為固定系統參數R，b，k，而將V=5，圖4(c)為固定系統參數V，b，k，令a=3，對于圖4(d)為固定V，b，a，k，由圖4(a)～圖4(d)的各個系統參數在不同α下的信噪比增益均呈現“先增后減”的單峰現象，可證明該系統在α噪聲下可產生隨機共振現象且系統參數b的搜索范圍小于V，a和R范圍。由圖4(e)，k為阻尼項在粒子運動過程中擁有阻礙粒子運動的功能，因此在實現隨機共振時，當系統采用較高阻尼比時系統達到共振時所需的噪聲能量更強，這一點可以從圖中阻尼比由0.1增加到1時，信噪比增益曲線逐漸右移說明，因此在微弱信號檢測時，可通過調節各個系統參數以及阻尼項使待測信號的信噪比增益達到最優值，從而檢測出目標信號。

2 變分模態分解

變分模態分解(Variational Mode Decomposition，VMD)是一種自適應頻率分解方法,每個模態由中心頻率和帶寬組成, 此過程可理解為迭代和搜尋變分問題的最優化,其中μk(t)為模態函數,具體求解步驟為

步驟1對于每一個μk(t)通過Hilbert得到其解析信號,利用exp(-jωkt)調制估計中心頻率

(15)

步驟2每個模態都能緊密地圍繞在各自中心脈沖頻率ωk附近,ωk的帶寬由以上解調信號的高斯平滑度來估算,則建立受約束的變分問題為

(16)

式中:f為原始信號;uk為模態函數;ωk為各個模態的中心頻率。

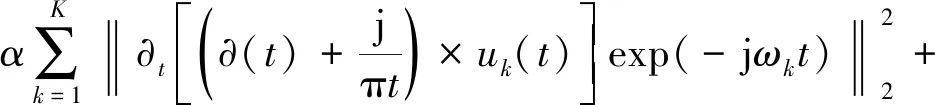
式中:α為懲罰因子；λ為拉格朗日因子。

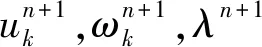
(18)

步驟5通過Parseval /Plancherel傅里葉等距變換將其轉換到頻域

(19)

通過ω=ω-ωk進行變量代換,然后將其轉換為非負頻率區間積分形式,最終求解的更新表達式為

(20)

(21)

算法流程如下:

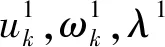
步驟2n=n+1開始整個算法的循環；

步驟3 利用式(20)和式(21)更新uk和ωk,k=k+1,k∈(1,K),K為窄帶模態函數分量個數；

步驟5 給定精度e>0,若滿足判定表達式

則迭代終止,否則返回步驟2。

3 仿真信號分析

3.1 諧波振動信號

旋轉機械廣泛應用在交通工具、航空發動機、發電機等系統中，其運行時的安全可靠是減少經濟損失、避免人身傷害的前提；因此若要保證機器的穩定，準確的健康監測與診斷系統對指示旋轉機械可能發生的初期故障具有重要意義，通常旋轉機械系統是通過產生的諧波振動信號獲取機器的運行狀態[22]，因此選取采樣頻率fs=5 000 Hz的諧波振動信號模型為

采樣點數N=10 000，原始信號中其中各次諧波的幅度值d(m)m=1,2,3=[1,0.8,0.5]，信號基頻f0=10 Hz，因此cos(4πf0t)和cos(6πf0t)是以f0為基頻的二次諧波和三次諧波，其中:ξ(t)是噪聲強度D=2的α噪聲，參數設置為α=1.2，β=0，σ=1，μ=0。由圖5(a)可知諧波振動信號完全被淹沒在α噪聲背景下，時域圖只能觀察到噪聲特性。在將時域信號利用FFT變換后求其相應的功率譜圖5(b)可知功率譜中特征頻率無法識別，因此需要借助隨機共振對信號進行非線性放大，但是由于隨機共振受絕熱近似理論的限制，而此時諧波振動信號的頻率遠大于1 Hz ，所以采用二次采樣對諧波振動信號壓縮等效為滿足條件的低頻信號，采樣壓縮比R=fs/fsr=1 000，二次采樣頻率為fsr=5 Hz。將淹沒在α噪聲中的諧波振動信號輸入到經典雙穩隨機共振系統，其中系統參數和阻尼比(a,b,k)=(1,1,0.5)，從圖5(c)可觀察到其特征頻率，但是在其高頻還存在噪聲頻率而且干擾頻率較多，因此采用式(13)對諧波振動含噪信號為輸入的式(4)進行求解，利用自適應參數尋優系統參數組合為(V,R,a,b,k)=(0.5,1,1,0.01,0.3)。經過混合型三穩態隨機共振系統后，圖5(d)是顯示諧波振動信號輸出功率譜圖，對比圖5(b)、圖5(c)相應功率譜可知隨機共振系統可對含噪信號進行非線性放大凸顯特征頻率，對比圖5(c)、圖5(d)混合三穩態共振系統較經典雙穩態系統在諧波振動信號特征頻率處均有較大程度的提高，能夠更好的協同噪聲放大信號，最大程度的吸收高頻噪聲能量轉化為低頻有用信號能量，使特征頻率更加明顯，而且準確的檢測出諧波振動信號，因此在α噪聲背景下檢測諧波振動信號混合三穩態系統優于經典雙穩隨機共振系統。

圖5 經典雙穩和混合三穩諧波信號檢測Fig.5 The harmonic vibration signal detection of the classical bistable and hybrid tri-stable system

3.2 調幅信號

旋轉機械完成旋轉動作的主要部件為轉子，轉子常常會發生與靜止件的碰撞摩擦，這時故障會引起振動信號的調制現象，因此有效識別和提取調幅振動信號調制特性對檢測轉子故障具有實際意義[23]。選取采樣頻率fs=20 000，采樣點數N=10 000，調幅振動信號

s(t)=A(m)(1+cos(2πf1(t)))sin(2πmf0t)+ξ(t)

其初始幅度參數為A(m)m=1,2,3=[0.8,0.5,0.2]，其中調制頻率f0=300 Hz，被調制頻率f1=30 Hz，ξ(t)是噪聲強度D=1.5的α噪聲，噪聲參數設置為α=1.2，β=0，σ=1，μ=0。圖6(a)為原始調幅信號時域圖形，在α噪聲背景下的調幅信號功率譜圖如圖6(b)，調幅信號已經完全淹沒在噪聲下，由于0～10 kHz內均有頻率點幅值，因此無法區別噪聲和有用信號。利用二次采樣對調幅振動信號壓縮等效為滿足條件的低頻信號，采樣壓縮比R=fs/fsr=10 000，二次采樣頻率為fsr=2 Hz，將淹沒在α噪聲中的諧波振動信號送入經典雙穩隨機共振系統，其中系統參數和阻尼比(a,b,k)=(1,1,0.5)，由圖6(c)可以看到在0～400 Hz內f0=300 Hz處功率譜幅值為579.1和f0+30 Hz處105.2,f0-30 Hz處126.4的譜峰值，400～800 Hz內只能觀察到2f0=600 Hz處270.4的功率譜幅值，2f0±30 Hz周圍存在著明顯的干擾噪聲頻率，而在800～1 200 Hz內3f0=900 Hz及3f0±30 Hz完全被噪聲所覆蓋，由此可知經典雙穩系統對調幅信號檢測不佳，利用自適應參數尋優算法獲得混合型三穩隨機共振系統最優參數組合及阻尼比參數大小為(V,R,a,b,k)=(1,1,5,0.3,0.5)，圖6(d)為經過混合三穩態系統的輸出功率譜圖,相比雙穩態模型而言混合三穩態系統在800～1 200 Hz內能觀察到3f0=900 Hz的譜峰值為1 042，對比圖6(c)、圖6(d)可知混合三穩態在轉子故障引起的調幅振動信號檢測中優點凸顯，不僅檢測信號的個數優于經典雙穩，更是在待測信號功率譜幅值方面高于一個量級，因此混合三穩態系統擴展了信號的檢測范圍。

圖6 經典雙穩和混合三穩調幅信號檢測Fig.6The amplitude modulated signal detection of the classical bistable and hybrid tri-stable system

3.3 周期衰減脈沖信號

軸承故障診斷中故障信號總是以沖擊級數的形式出現[24]。因此選擇含有α噪聲的周期性單邊衰減脈沖離散信號作為強噪聲下的模擬軸承故障信號，其單周期衰減脈沖表達式為

s(t)=Aexp(-gt)sin(2πfnt)

采樣頻率為fs=20 000，固定頻率為fn=1 200，故障頻率為f0=200，幅度為A=0.8，衰減率g=600，采樣點數N=10 000，圖7(a)周期衰減脈沖信號時域圖，在原始信號中加入α噪聲，噪聲強度D=0.2，參數設置為α=1.6和β=0，σ=1，μ=0。傅里葉變換后求得其功率譜如圖7(b)中并沒有觀察到故障頻率，最大幅值處為固定頻率處。0～500 Hz內f0幅值過小，經過采樣壓縮比R=fs/fsr=10 000，二次采樣頻率fsr=2 Hz后送入經典雙穩隨機共振系統(a,b,k)=(1,1,0.5)，由圖7(c)可以看到在0～1 200 Hz內處功率譜幅值為2.751，譜幅值較低且整個帶寬內都存在噪聲，噪聲利用率較低；因此利用式(12)對含噪周期衰減脈沖信號為輸入的式(4)進行求解，利用參數自適應尋優算法獲得最優參數組合為(V,R,a,b,k)=(3,5,1.7,0.04,0.5)，圖7(d)為經過混合三穩態系統的輸出功率譜圖，800～2 000 Hz處已無噪聲存在，且能夠檢測出故障特征頻率外的二倍頻及三倍頻，對比圖7(c) 、圖7(d)可知混合三穩態更適合于軸承故障的診斷，能夠清晰、準確的提取出軸承故障的特征頻率。

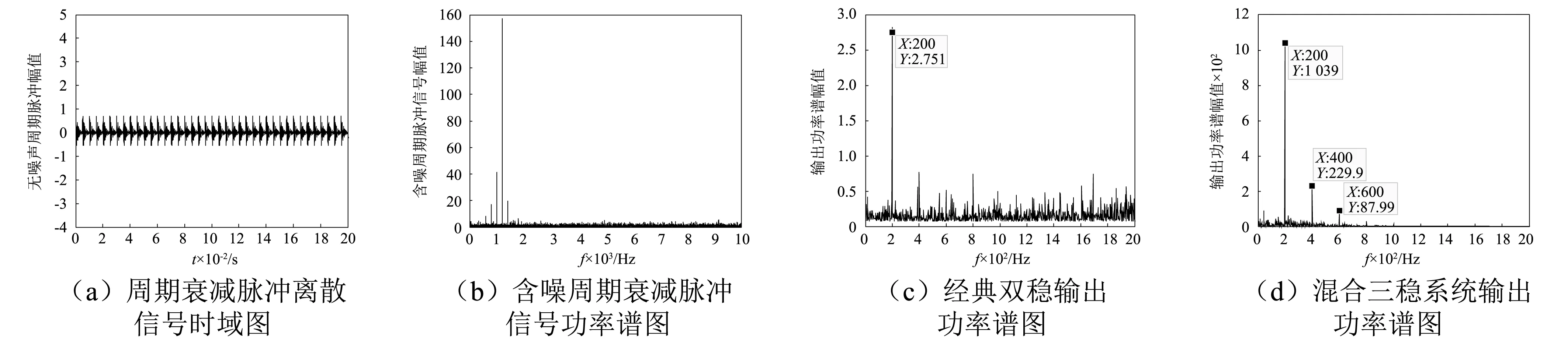
圖7 經典雙穩和混合三穩周期衰減脈沖信號檢測Fig.7 The periodic unilateral attenuation impulse signal detection of the classical bistable and hybrid tri-stable system

4 深溝球軸承實驗驗證

滾動軸承故障信號具有非平穩性、微弱性，常常淹沒在強大的背景噪聲中難以發現和提取，極易對工程應用造成不可估量的損失，軸承故障常常以倍頻形式存在，為驗證變長模態分解與混合三穩隨機共振組合系統在軸承故障信號檢測的實用性。采用西儲大學電氣工程實驗室型號為6205-2RS JEM SKF的深溝球軸承裝置[25]。軸承轉速1 797 r/min采樣頻率fs=12 kHz；表1滾動軸承主要計算參數，由式(22)計算外圈故障頻率為107.3。

圖8 6205-2RS JEM SKF實驗與采集裝置Fig.8 6205-2RS JEM SKF experimental equipment

表1 6205-2RS JEM SKF軸承參數

軸承故障信號頻率計算

(22)

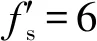
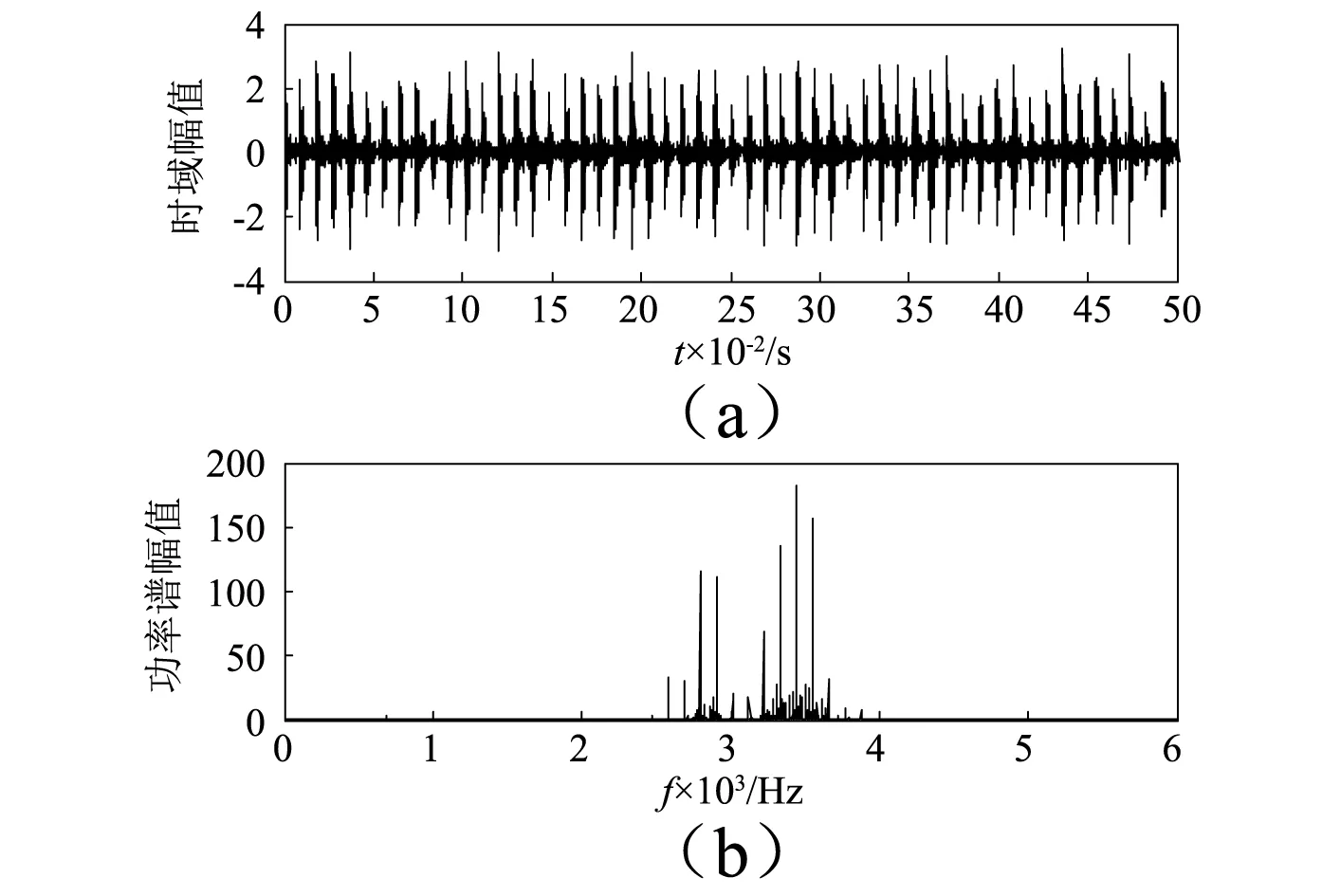
圖9 故障信號的時域圖和頻域圖Fig.9 The time domain and frequency of the fault signal

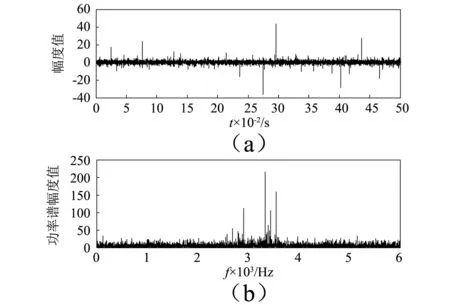
圖10 加噪信號時頻圖Fig.10 The time domain and frequency of the noisy fault signal

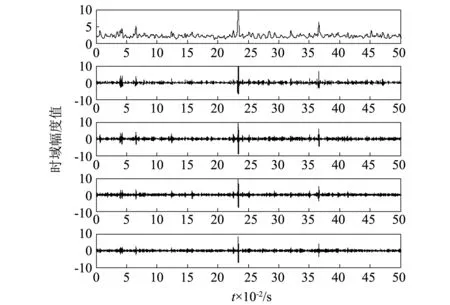
圖11 變分模態分解時域圖Fig.11 The time domain of the VMD

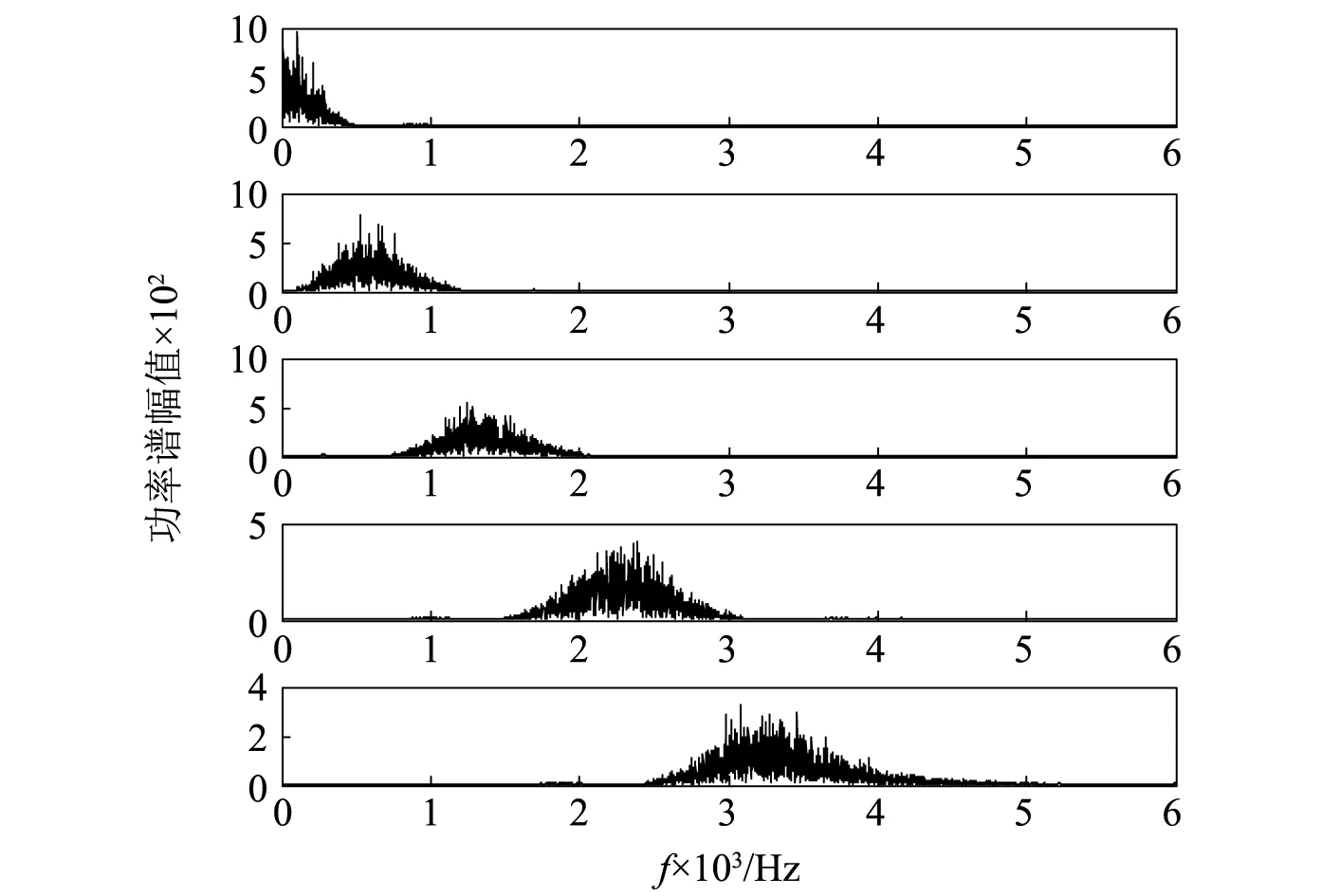
圖12 變分模態分解功率譜圖Fig.12 The frequency of the VMD

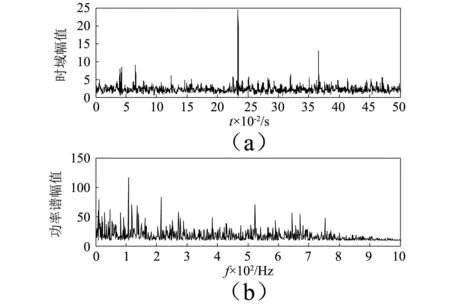
圖13 重構信號時頻圖Fig.13 The time and frequency of the reconstructed signals

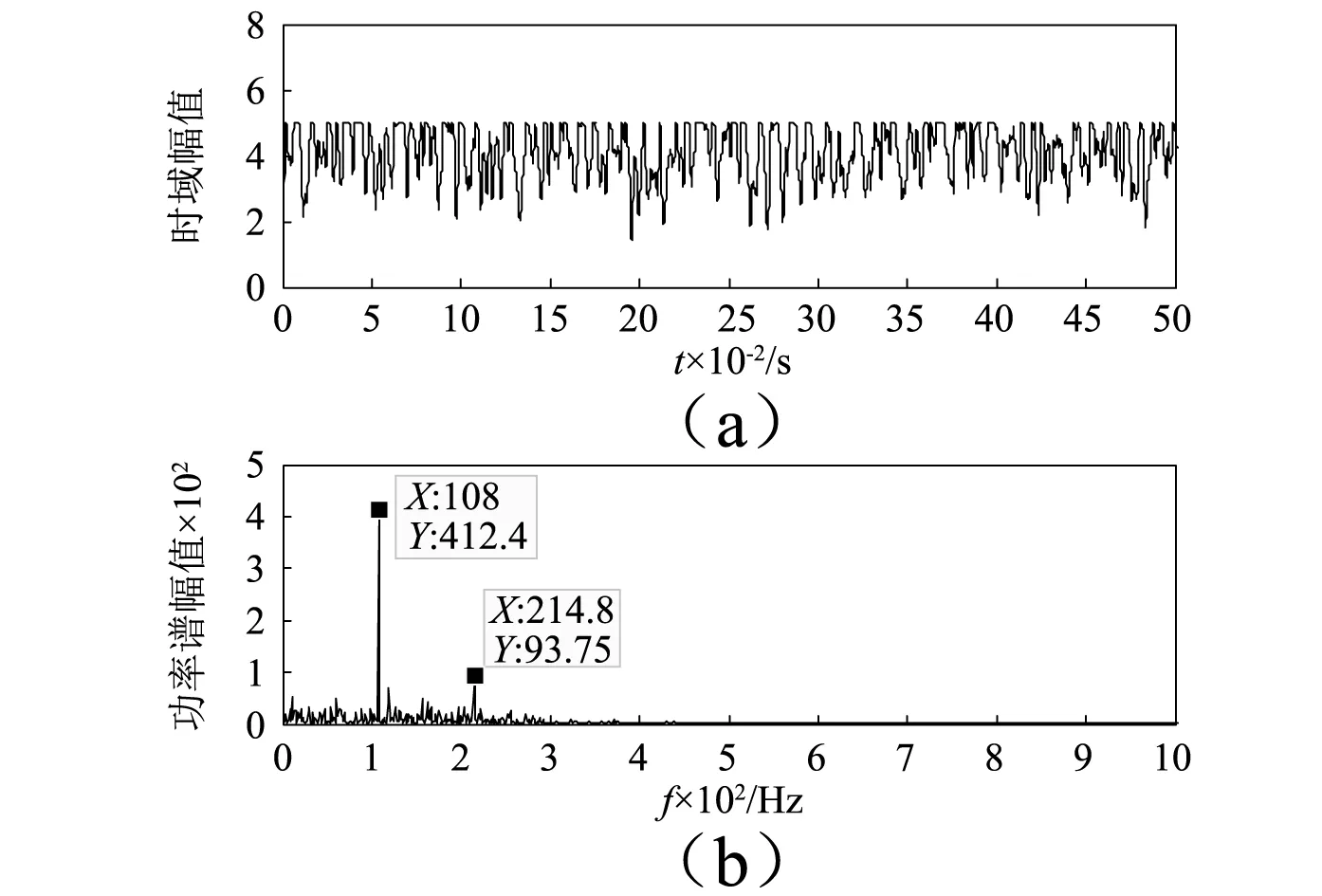
圖14 組合系統輸出時頻圖Fig.14 The time and frequency of combined system

5 結 論

本文將Woods-Saxon單穩態系統與混合雙穩態系統組合成一種新型的三穩系統，稱為混合型型三穩隨機共振系統。該系統不僅保留了Woods-Saxon對于軸承信號檢測的優良性，而且擁有三穩態對噪聲充分利用的特點，文中以信噪比增益為衡量指標，利用自適應算法通過調節系統參數(V,R,a,b,k)實現隨機共振的最佳輸出，而且利用噪聲的變化證明了混合三穩態信噪比增益符合隨機共振的典型先增后減特性，針對α噪聲背景的諧波振動信號、調幅信號、周期衰減脈沖信號進行檢測，結果表明：混合三穩態系統在三者檢測中均優于經典雙穩態系統，能夠檢測出經典雙穩態未檢測出的待測信號。為了更好的將系統應用于實際，將變長模態分解與混合三穩態結合，能夠實現更近一步的聚集目標頻率能量,通過實際軸承信號驗證，該系統在復雜噪聲背景下不僅檢測出軸承特征頻率而且清晰顯示其倍頻，充分的證明了該系統在故障檢測效果的良好性，因此本文為所提系統的應用提供了有意義的參考價值。