等離子體參量的發射光譜診斷的研究

孫殿平

(華東師范大學 a.精密光譜科學與技術國家重點實驗室;b.物理與材料科學學院，上海 200062)

1 概 述

等離子體是 “物質第四態”， 已被廣泛地應用于激光器、光源照明、能源、物質與材料加工、環保與宇宙科學、化學合成、表面處理、薄膜制備、閃電放電過程研究等諸多領域[1-12]. 因此其電子密度、粒子密度、溫度等參量的診斷成為物理學研究的重要課題之一[1,7].

研究等離子體參量有實驗診斷、理論解析和數值模擬3種研究手段[13-18]. 由于等離子體中的物理化學過程極其復雜，使得理論解析以及計算機數值模擬很難準確地獲得等離子體的各種參量，這就顯現了等離子體實驗診斷的重要性. 常用的實驗診斷手段主要有光學診斷技術、Langmuir探針[19]和質譜技術[13].

光譜學診斷方法是用等離子體的發射光譜或吸收光譜診斷等離子體溫度、密度和化學組分等參量的方法[16-17]. 此法是在20世紀50年代初期由H.邁克等人較為系統地提出的[16]，起初應用于天體物理和基礎實驗研究，應用于實驗室等離子體最早是從高溫聚變等離子體診斷開始的，后來又應用于航天環境模擬、化工冶煉、熱加工和能源等方面的實驗中.

等離子體發射光譜作為無干擾方法可用于多種等離子體物理特性的診斷，如等離子體的電子溫度、電子密度、激發溫度甚至某些動力學過程. 針對高溫等離子體，其中的連續輻射光譜可用于電子溫度的測量[20]，線狀譜線的Stark效應[21]可以用于電子密度的測量，而線狀譜線的強度分布可以用于激發溫度的診斷[22]. 針對低溫等離子體，上述效應雖然較弱不足以可靠診斷等離子體，但也促進了許多其他技術的發展，高分辨發射光譜的譜線線型分析[23]是等離子體中激發過程動力學機理的一種有效分析手段.

在低溫等離子體診斷中，發射光譜學的早期應用主要有兩方面，即刻蝕和沉積過程[24]的機理診斷以及非穩態等離子體發光過程的時間行為分析. 瞬態等離子體的非平衡特性明顯，重新發展相應的發射光譜診斷技術的分析理論顯得十分重要. 例如：利用譜線的Stark展寬測量電子密度的理論模型必須加以修正. 利用譜線的Stark移動測量電場分布[24]的原理也需要改進. 利用分子光譜譜帶[25]分析實現溫度測量是發射光譜診斷的重要內容，但是瞬態等離子體的非平衡特性使得傳統光譜模擬理論方法也必須加以修改.

發射光譜法由于儀器系統簡單、選擇性好、適用范圍廣、環境條件要求低，可以作為一種便攜式在線無接觸診斷方法. 但是由于大量干擾譜峰的存在，在實踐中這種方法主要用于簡單分子的等離子體診斷.

然而發射光譜的定量分析卻是一個難點，發展定量分析的理論和方法是十分必要的. 另外對于不發光物種的診斷是間接的. 可利用吸收光譜技術定量測量不發光物種成分、濃度、溫度等參量[26]. 20世紀60年代，開始用激光光譜診斷法對等離子體狀態和輸運性質進行實驗研究[8,27].

2 實驗測量裝置

常見的發射光譜測量實驗裝置如圖1所示，主要包括2部分：等離子體產生裝置和光譜測量裝置[8,28].

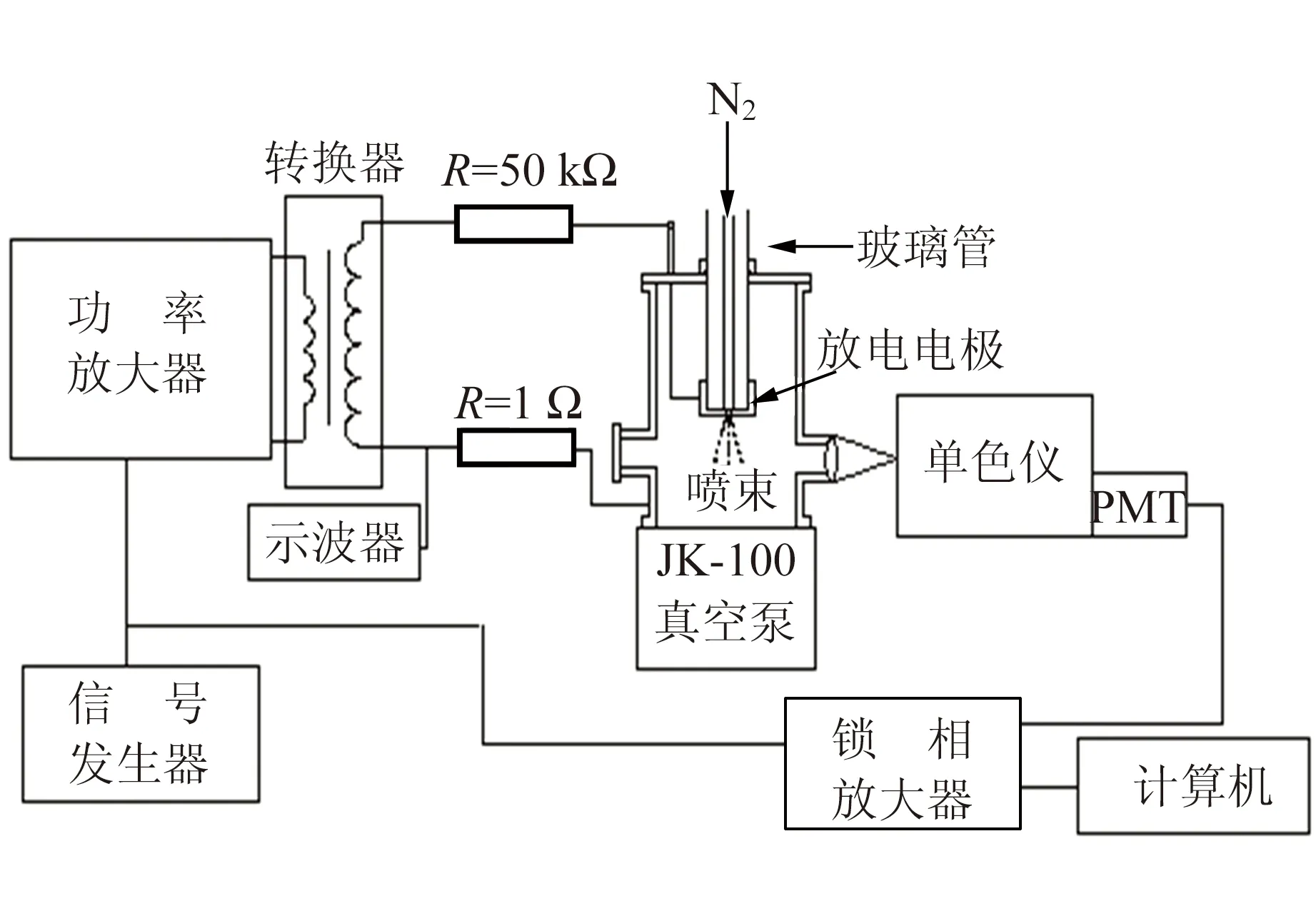
圖1 實驗裝置示意圖

交流電壓產生等離子體，其氣體瞬態分子(如離子分子、自由基分子和激發態分子等)在每個放電周期發生2次濃度的突然變化，因此鎖相放大器采用1f參考信號進行解調來獲得速度調制光譜，2f參考信號進行解調來獲得濃度調制光譜. 探測到的信號經由鎖相放大器解調后輸送到電腦記錄和讀取[29]. 它是一種內調制光譜技術,具有很高的靈敏度. 若兩電極放電不均勻對稱，通過濃度調制光譜分別在1f和2f參考頻率上進行測量，可以了解電極的放電強度及氮離子分子產生的微觀過程[28，30].

脈沖直流放電技術實驗裝置如圖2所示[31]，探測信號經Boxcar 檢測采集數據后送入計算機處理，對于脈沖激光產生的等離子體的研究也可采用類似光譜采集系統[31-33]. 通過Boxcar或采用計算機軟件控制[34]，可以測量等離子體中不同壽命粒子的發射光譜信號的時間演化特性[35-36].

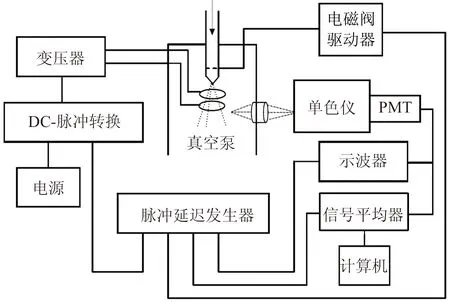
圖2 文獻[31]中的脈沖直流放電實驗裝置示意圖

3 等離子體參量的發射光譜測量

發射光譜攜帶著大量的信息：1)光譜線的頻率，據此可確定等離子體的激發物種;2)光譜線的強度及強度分布;3)光譜線的線型. 因此原則上利用等離子體的發射光譜能提供診斷等離子體溫度、電子密度、激發、電離狀態和化學組分及各成分的相對含量等[7]，還可以獲得分子的轉動溫度、等離子體的激發溫度等重要參量[36-38].

3.1 等離子體的溫度及其診斷

在多數情況下，等離子體會偏離局部熱力學平衡狀態，這樣就不能用單一溫度描述出等離子體的行為，需區分討論激發溫度、振動溫度、轉動溫度等不同溫度的概念. 通常，如果等離子體中每種組分的速率都分別滿足1種Maxwell速率分布，針對某種粒子不同類自由度的平均能量就可以定義不同的溫度，那么不同的組分就可用不同的溫度來描述. 這樣等離子體中發生的不同過程就可用不同的溫度來表征. 通常的光譜法測溫，總是假定等離子體處于局部熱力學平衡和光薄狀態[36-38].

3.1.1 平動溫度

離子、原子的平動能量對應平動溫度. 所以平動溫度測量可用離子或原子發射譜線的多普勒展寬法測量. 線狀譜譜線的多普勒展寬計算平動溫度的方法是利用等離子體中的粒子熱運動引起的譜線的展寬效應[38-40]. 首先確定譜線的中心波長λ0，然后，確定該波長譜線的寬度Δλ1/2，再用譜線多普勒展寬公式:

(1)

式中，kTa為計算原子的溫度,單位是eV，ma和A分別是被測原子的質量和相對原子量，c是真空中的光速.

多普勒展寬測溫法只適用于粒子數密度較小、低壓、稀薄氣體的情況(例如分子束中)，譜線加寬主要是由效應引起的.

從式(1)可知，溫度愈高，多普勒加寬愈大，而在相同溫度下，輕粒子的譜線加寬大于重粒子的，故此法常采用氫譜線作為測量線. 在低溫等離子體測溫范圍內，加寬量很小，僅為0.01～0.000 1 nm，必須用高分辨率光譜儀才能測定.

3.1.2 轉動溫度

分子氣體溫度不太高時會激發轉動自由度. 轉動態分布處于熱平衡時，分布在轉動狀態J的分子數為[37]

(2)

式中，NJ′表示原子、離子或分子處于給定的轉動能級的布居數，Be為轉動能級的轉動常量，N為總粒子數，Ttot即為轉動溫度. 由于所用單色儀的分辨率不同，得到不同分辨率的發射光譜，因此不同分辨率的轉動光譜有對應的不同轉動溫度測量方法.

1)轉動譜線可分辨的高分辨轉動光譜

對于轉動分辨清晰可見的光譜，P,Q,R支的間距比較大，不必考慮3支的重疊. 根據每條譜線的強度和對應的轉動量子數，可以用

(3)

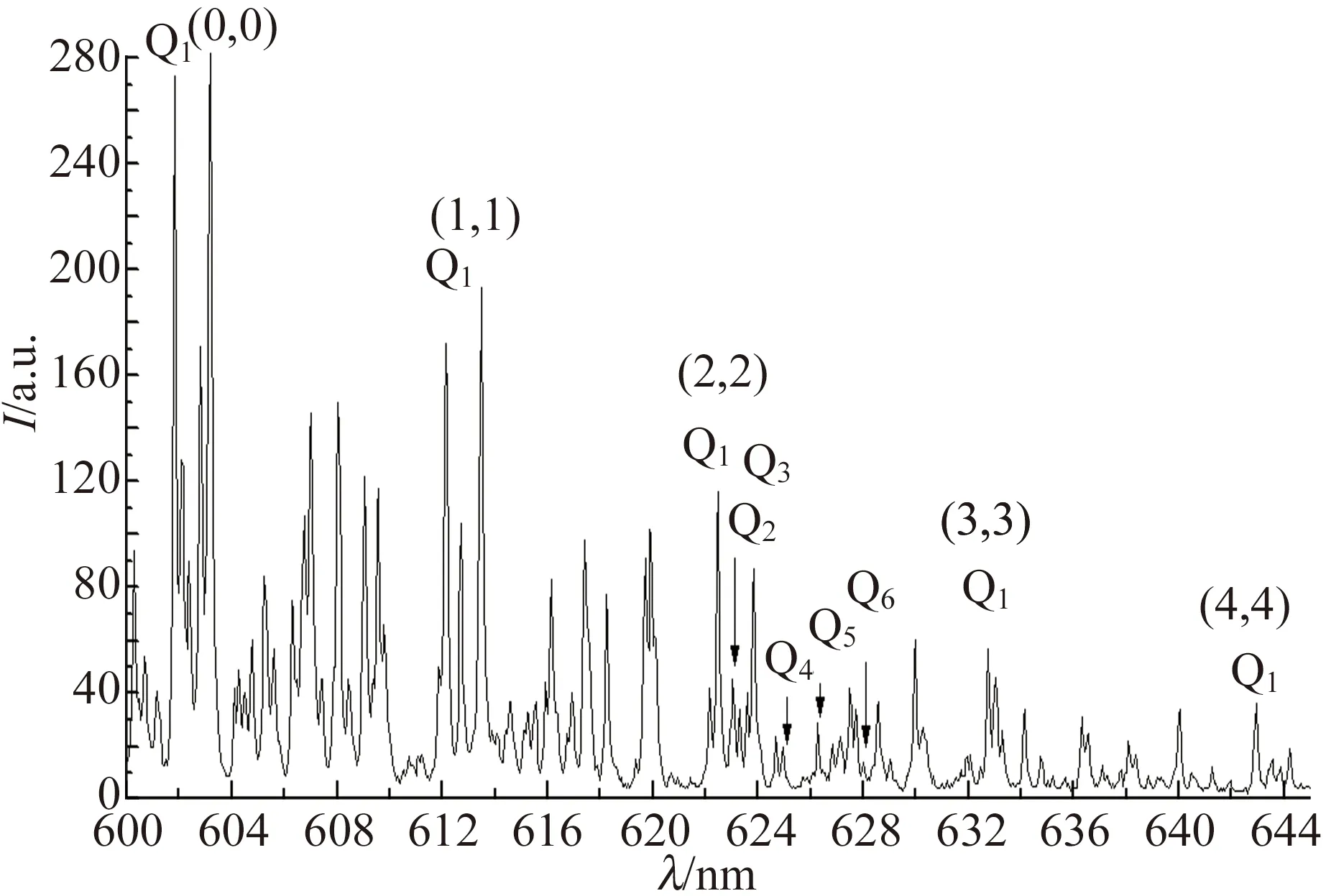
圖3 文獻[41]中氫分子帶的振轉結構光譜圖

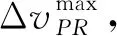
(4)

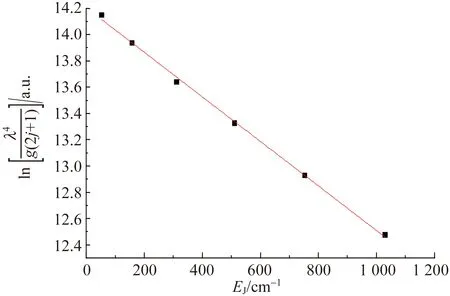
圖4 文獻[41]中氫分子放電Fulcher-α帶(2,2)Q支發射光譜的玻爾茲曼曲線

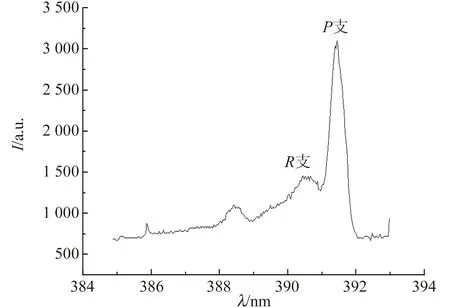
圖5 文獻[30]噴束中的電子態(0，0)振動帶躍遷譜線

3)P支和R支不可分辨的轉動光譜帶

對P,Q和R支有重疊，特別是三重態的躍遷,如CO轉動譜線(如圖6所示)[8]，各支重疊嚴重，很難分辨. 對于這樣的譜帶，可編寫程序進行模擬，通過與實驗譜線相比，可以得到轉動溫度.

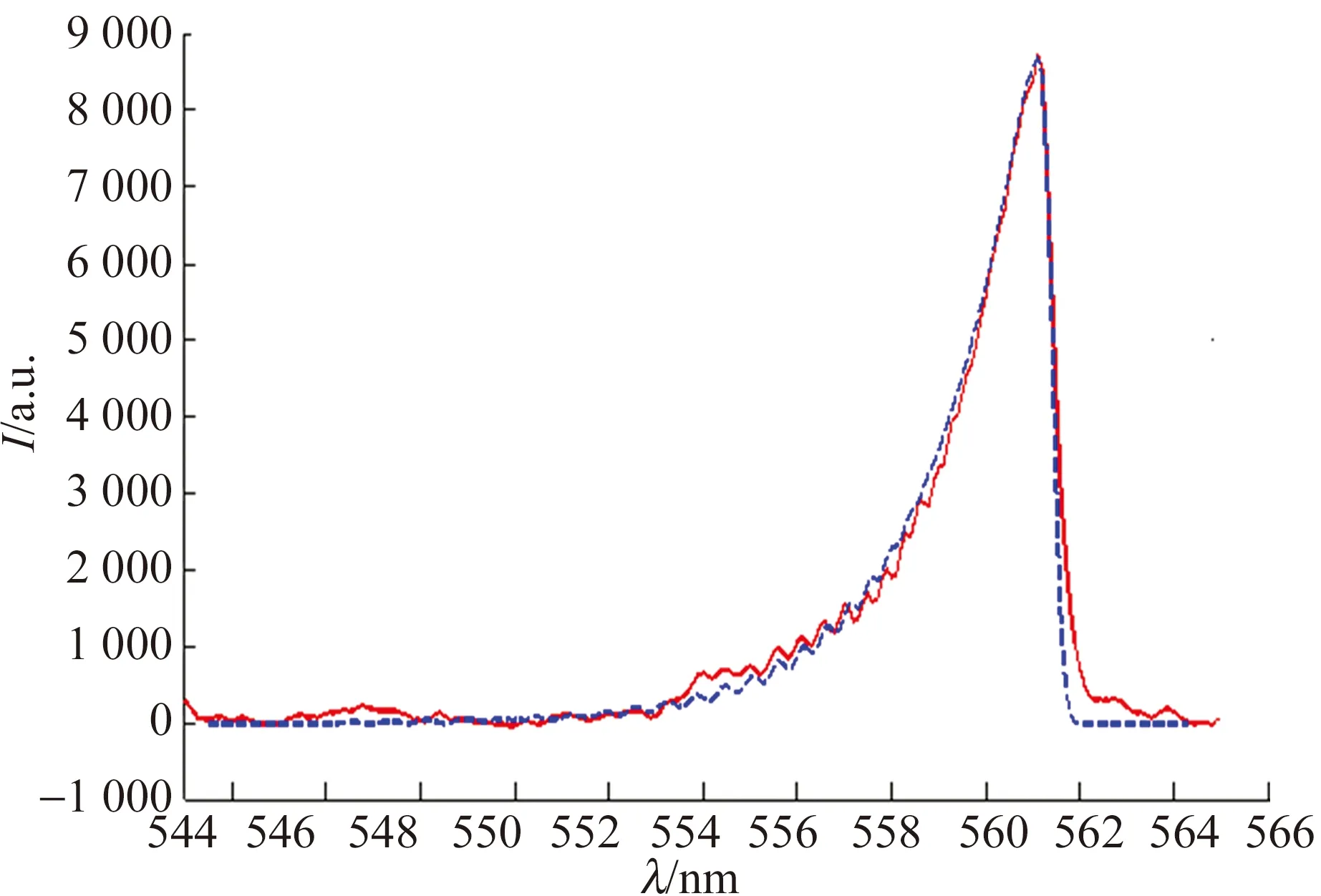
圖6 文獻[8]中CO B1∑→A1Π(0,3)發射光譜與轉動溫度在450 K時的發射光譜模擬

在放電體系中，激發態的形成有2種機制:一種電子碰撞激發，另一種是反應形成. 對于電子碰撞激發過程中，分子角動量是守恒的，因此由NJ′可以推測下能級的轉動態分布情況，而反應生成激發態的過程分析則相當復雜.

3.1.3 振動溫度

在同一電子態的不同振動態v中的粒子數Nv為[8,37]

(5)

式中,Qv為配分函數，Tv即為振動溫度，G(v)為振動能量. 等離子體中分子的振動溫度不受重視，但有學者[42]認為通過增強等離子體的振動激發，反應物將易于吸附到催化劑上，并能有效克服反應勢壘，使能耗降低，因此分子的振動溫度在化學合成中成為一個重要參量.

1)譜線可分辨振動譜的振動溫度

由于振動函數是歸一化的，對v的前進組帶，所以在一般情況下，同一電子態的振動躍遷中，電子躍遷矩Re為常量，可得[8]：

(6)

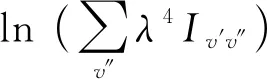
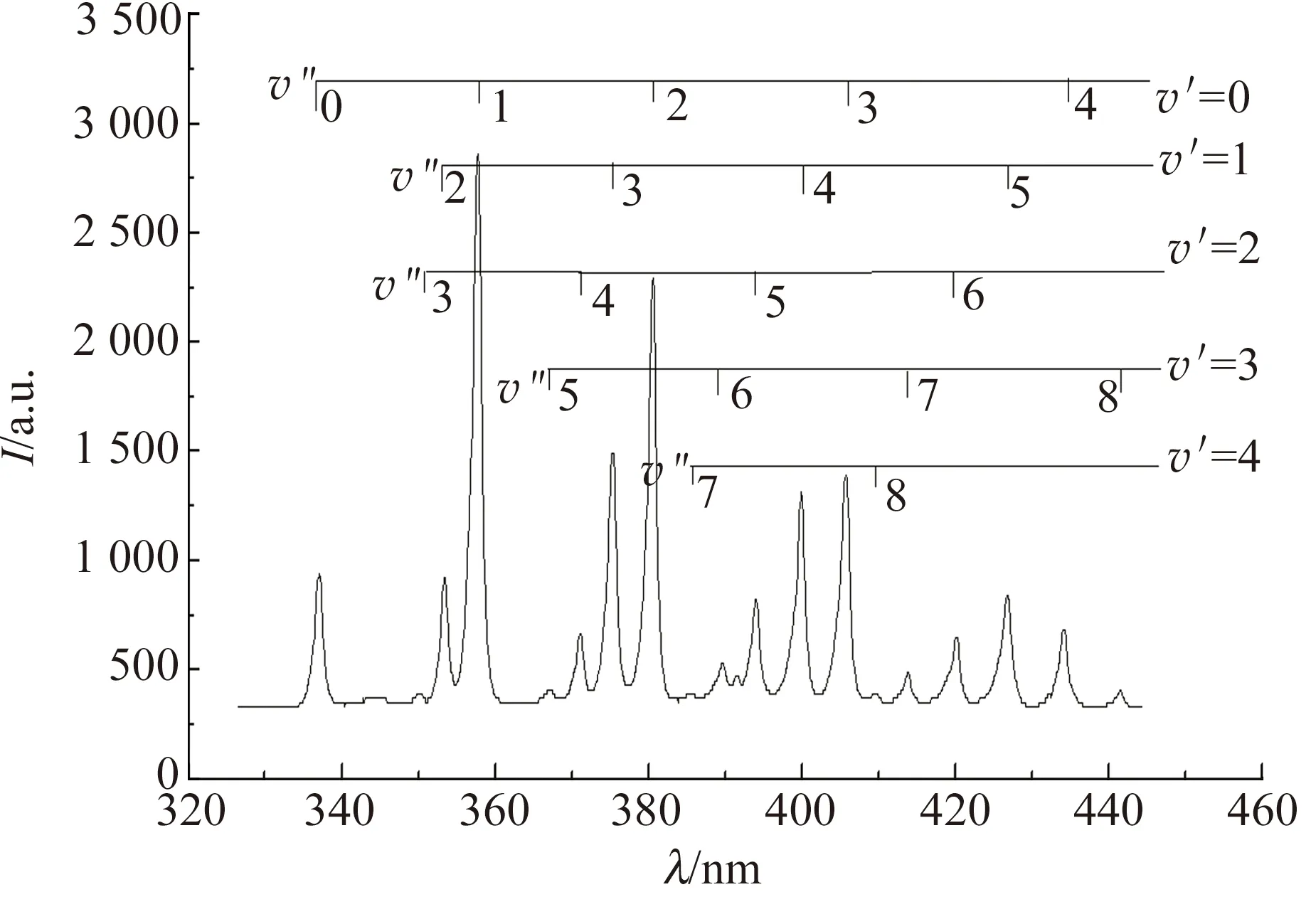
(a) 玻璃管中探測到的N2發射光譜

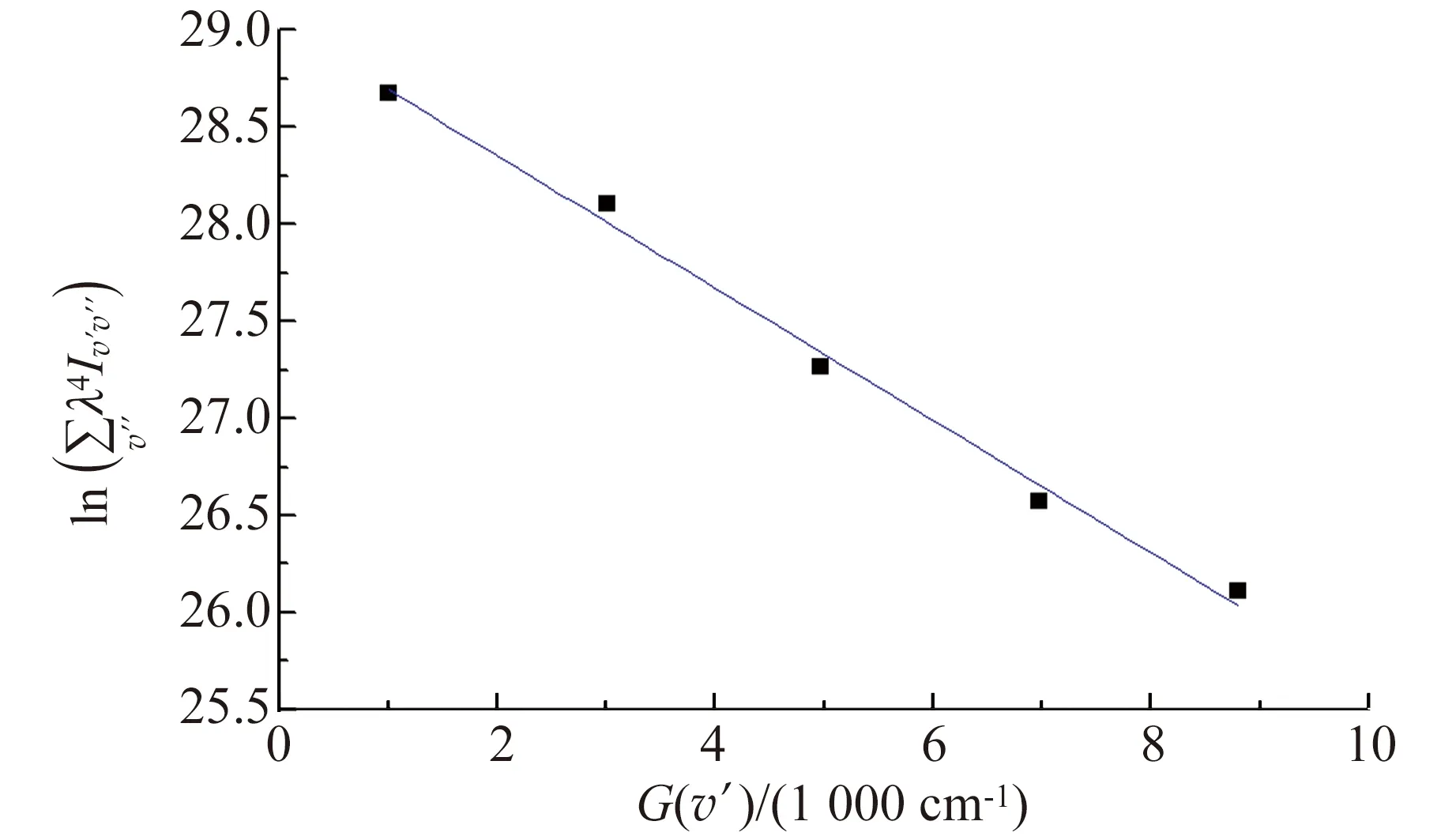
(b)玻璃管中N2C3πu振動能G(v′)玻爾茲曼圖圖7 文獻[30]中玻璃管中探測到的N2發射光譜及玻爾茲曼圖

2)不能分辨振動轉動譜線的振轉溫度

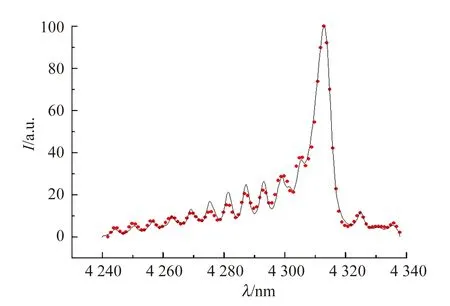
圖8 文獻[44]中CH(A2Δ-X2Π) (0，0)帶發射光譜及LIFBASE程序模擬光譜

對于由幾個振轉動帶的光譜疊加而成不能分辨振動轉動譜線,例如CH(A2Δ-X2Π)帶的發射光譜[44]，如圖8所示. 可以采用LIFBASE程序[43-44]通過理論模擬來獲得較為精確的振動溫度與轉動溫度.

利用上述方法，通過對在分子預解離或與其他粒子碰撞造成轉動能級非熱力學平衡造成[45]雙溫度分布或多溫度分布研究，可以進一步得出內能重新分配機制[46-48]，還可對燃燒過程中振動能平動能轉化和分配機制進行研究[48].

3.1.4 電子溫度

電子溫度用來表征等離子體中粒子和電子碰撞過程的熱平衡狀態，也稱電子激發溫度. 如果處于某一能量范圍的激發態上的粒子通過電子碰撞過程達到了某種局部平衡狀態，那么處于第q能級的粒子數密度nq由玻爾茲曼分布給出[2,7-8]

(7)

式中，Z為配分函數，gq為統計權重，Eq是q能級的能量，Te為電子溫度. 在等離子體形成的初始階段，連續背景輻射較強，可以利用連續背景輻射來確定電子溫度；在中、后期階段，連續背景輻射較弱，而原子、分子、離子的分裂譜線很強，這時應使用這些分立譜線. 通過測量激發態粒子的光輻射強度，可以得到相應激發態的粒子數布居數之比，進而利用玻爾茲曼圖解法可以得到電子溫度. 電子溫度與某一能量范圍的電子數密度相關.

1)兩譜線法

采用等離子體局部熱平衡近似，可以通過測量相同原子2條譜線的相對強度來確定等離子體的電子激發溫度[2,8]

(8)

式中下標1和2是分別指第一與第二條譜線.

兩譜線法可用于同一元素的2條中性原子譜線的強度比，也可用屬于同一元素的2條離子譜線的強度比. 在選擇發射譜線計算電子溫度時，還需滿足E2-E1>kTe. 為測量電子激發溫度，選用相距較近的Ar 763.51 nm和772.42 nm光譜線對電子溫度進行分析.

2)玻爾茲曼斜率法

如果有足夠多的譜線，其激發能及躍遷概率等數值為已知，則當測得它們的強度后，可由繪出曲線，如圖9所示. 式中，C為常數，Ei為能級，單位eV. 溫度Texc可由直線斜率求得.

(9)

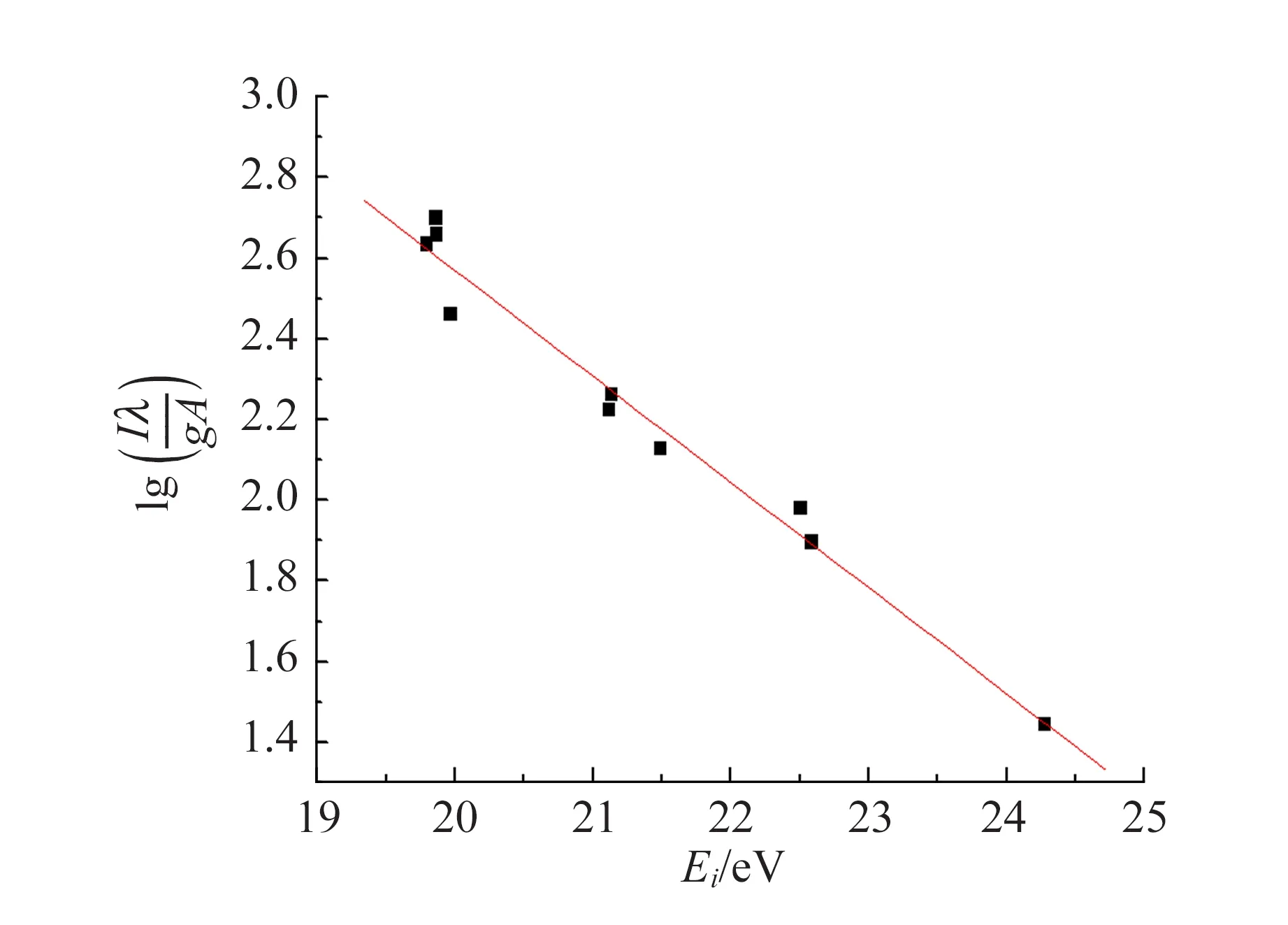
圖9 文獻[8]噴束中氬氣放電發射光譜的玻爾茲曼曲線

使用玻爾茲曼斜率法時應注意的問題很多，如所選譜線的躍遷概率應有可靠的值，譜線應無自吸收的影響，而且譜線組的激發能差值應盡可能大，所選譜線的強度隨等離子體溫度的變化應該很靈敏等. 玻爾茲曼斜率法的優點：一是應用了多條譜線的信息，因此測溫精度較高；二是此法還可用來驗證哪些點(即哪些譜線)處于局域熱力學平衡.

利用電子溫度，可以監控等離子體噴槍特性、激光焊接過程、材料加工和照明形成等過程[49-50].

3)連續光譜求電子溫度

在等離子體中，韌致輻射與復合輻射的相對貢獻與等離子體溫度密切相關，各種輻射和吸收機制共同作用達到平衡. 通過等離子體光譜的連續光譜，借助文獻[51-52]公式作計算機模擬可得電子溫度. 因此，此法應用到激光等離子體的電子溫度、電子密度以及其隨時間的演化機制研究[52-53].

3.1.5 電離溫度

如果把玻爾茲曼分布應用到連續狀態，就是相當于電離的情況. 粒子的分布用沙哈方程描述，與這個電離自由度相聯系的溫度定義為電離溫度. 一次電離的沙哈方程形式為[7]

(10)

式中ni和ne分別是一次電離原子數密度和電子數密度，nα為中性原子數密度，Z1和Z分別為一次電離離子的配分函數和中性原子的配分函數，Ei為電離能，Te是電子溫度，Ti是電離溫度.

3.2 電子密度

為了對某種等離子體系作出有意義的理論模型，就必須很好地了解氣體動力學截面、帶電粒子與不帶電粒子的碰撞截面、不同粒子的密度和溫度等數據．在上述參量中，頭等重要的是電子密度ne的數值及其隨時間的變化，因為許多動力學反應速率直接或間接地依賴于電子密度[54].

3.2.1 根據半峰寬計算電子密度

當等離子體的溫度比較低，電子密度在1020～1024m-3范圍內，譜線的線型又是洛倫茲線型時，譜線展寬主要機制是發生輻射躍遷的原子受到德拜球內離子電場作用產生(準靜態近似)的斯塔克能級分裂. 一般來說中性粒子引起的碰撞展寬和共振展寬可以忽略, 最終的譜線輪廓由斯塔克效應和多普勒輪廓決定. 當電離度不小于1%時, 由帶電粒子的長程庫侖力作用所決定的斯塔克效應占優勢. 對于氫原子，斯塔克效應是線性展寬，它的譜線展寬與電子密度有關，這時譜線輪廓的半峰寬Δλ1/2與電子密度關系為

(11)

式中，Δλ1/2是歸一化輪廓的半峰值寬度，α1/2其數據可查文獻[54]，例如Hβ的α1/2=0.087，ne的單位為m-3. 對于其他非類氫原子，斯塔克效應為非線性展寬，但近來一些文獻也對類氫原子的譜線展寬測量電子密度進行探討，如Al Ⅱ 281 nm譜線和Hα譜線的斯塔克加寬測得結果近似很好；文獻[55-56]利用近似公式Δλ1/2=αne,得到Ar 415. 86 nm譜線,α=2.30×10-18nm/cm3；ArⅠ 430. 01 nm譜線,α=2.27×10-18nm/cm3. 文獻[57]討論了考慮電子溫度影響時，利用弧室內和弧室出口等離子體射流的ArⅠ430 nm譜線，根據經驗公式

lnne=58.241+0.992 ln Δλ1/2-0.414 lnTe

(12)

計算等離子體射流的電子密度. 根據式(12)討論了在氬等離子體射流方向上, 存在著電子溫度和電子密度的梯度分布.

對于除氫元素之外的其他元素的發射譜線，Griem 以列表的形式分別給出了中性原子(He Ⅰ～ Ca Ⅰ和Cs Ⅰ)和一價離子譜線(Li Ⅱ～ Ca Ⅱ)的斯塔克加寬和頻移參量[54]，利用他們的計算數據和實驗結果對照，就能估算等離子體中的電子濃度.

利用斯塔克效應進行診斷的一個優點是，由于它是僅與電子密度有關的效應，與溫度關系極微，即與等離子體是否達到熱平衡關系不大，因而無論是瞬變等離子體還是準穩態等離子體，都可以應用斯塔克效應進行診斷.

3.2.2 根據光譜上可分辨的譜線極限估計電子濃度

等離子體中，由于電荷場的相互作用，原子和原子性離子的輻射譜線的半寬度，隨著光譜項中的主量子數增加而增大，以至使相鄰譜級間隔減小，甚至重疊. 隨著電子濃度增大，這種效應將擴展到較小主量子數的光譜項，即當電子濃度增大時，可分辨譜線序列的極限向長波長偏移. 因此可分辨譜線的極限與等離子體中的電子濃度是有關的. 如圖10所示，H原子光譜中可測到λ=383.498 nm原子譜線，對應nmax=9.

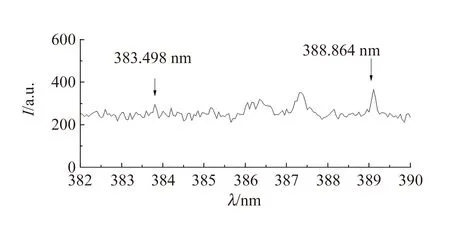
圖10 文獻[41]中等離子體中氫原子譜線

經計算，得出等離子體中電子濃度ne與可分辨的最后一根巴末耳譜線的主量子數nmax之間關系為[8,58]

lgne=23.94-7.5lgnmax-

(13)

(14)

其中，ND和λD分別是德拜屏蔽球內的電子數目和德拜屏蔽球半徑，Zp是輻射粒子的電荷數，中性粒子Zp=0，單荷正離子Zp=1.Ze是輻射粒子的核電荷數數目，Ze(H)=1，Ze(He)=2. 只要測出可分辨的那個主量子數nmax，知道Zp，Ze和Te后就可利用式(13)～(14)算出電子濃度ne. 使用式(13)～(14)測定電子密度，其誤差幾乎等于一倍．原因在于:“最后可分辨”譜線并不能嚴格確定．不過，這項技術還是有用的，得出的公式也將會適用于所有的原子，而不僅是類氫原子.

4 結束語

發射光譜是一種時空分辨性能良好的無干擾診斷技術. 它不僅能診斷出激發態物種，而且通過光譜解析還能獲得等離子體參量的諸多信息，但以前的理論一般都是建立在平衡等離子體條件下的，因此發展出對于非平衡等離子體的光譜進行準確解析的理論非常具有必要性和重要性，因為工業大規模使用的一般都是非平衡等離子體[59-63].

冷等離子體廣闊的應用前景，必將推動對其內部物理化學反應機理的深入了解，這就對等離子體物種及參量的精確實驗診斷提出了更高的要求. 一方面，應該不斷改進現有的診斷手段和探索新的實驗方法，另一方面，由于一種診斷手段通常只能探測某一種物種或參量，所以將幾種診斷手段聯用[32,64]，并充分發揮各自的優點，將有助于準確、全面地診斷等離子體的各種物種和參量.