小世界網絡理論在城市公共交通線網優化中的應用

吳亞萍

摘要：隨著社會經濟的不斷發展，城市交通在城市發展中所占據的地位不斷提高，其自身存在的問題也在不斷地出現，對城市內部的交通進行優先發展可以優化交通資源的利用效率，也可以逐漸解決城市的擁堵問題。優先發展公共交通的關鍵部分就是對公共交通網絡進行優化，從而促使公共交通競爭力得到提高。因為公交線路的聚集性比較高和平均最短站間路徑小，從而對小世界效應進行了反映。以小世界網絡理論的效率理論為基礎，研究了小世界在公交網絡中網絡理論的擬合問題，在公交網絡優化過程中給出小世界網絡理論應用方法。并以杭州市主城區中心區公交線網的應用為例說明了該方法的應用。

關鍵詞：小世界網絡;公交線網;全局效率;局部效率優化

中圖分類號：G434? ? ? ? 文獻標識碼：A

文章編號：1009-3044（2019）19-0263-02

1 引言

在城鎮化和交通汽車化的發展環境下，城市交通供給和需求之間的矛盾一天天突出，目前已經發展為在城市長期發展中急切需要解決的問題。通過對國內外相關理論的研究以及對城市交通建設現狀進行實地考察，優化現有常規公交系統、建立智能交通網絡是解決交通擁堵和環境污染等問題的根本出路。現在，在國內普通的公交線路優化過程中，基本上是建立數學優化模型的理論研究。這些措施對于解決公共汽車規劃過程中遇到的實際問題的效果不是很大，因為數據是很難被全部收集到的，這些措施也過于理想化，難以被實際操作。面對這些問題，本文主要在其他學者研究的基礎之上，根據公交線網的實際優化成果及目前的研究情況，根據小世界網絡理論提出了公交網絡優化措施。將小世界網絡的統計特性應用到公共交通網絡中。以杭州市為例，對公共交通網絡的優化進行了研究。經過分析公交網絡抽象模型，在眾多措施中選擇了最好的網絡方案，使得公交網絡的傳輸效率得到提高，以及網絡的容錯能力也被提高了。結合定性和定量分析，根據實際情況提出更具操作性的優化方案，為相關部門和企業提供決策支持。

2 模型與特性分析

2.1 小世界網絡模型

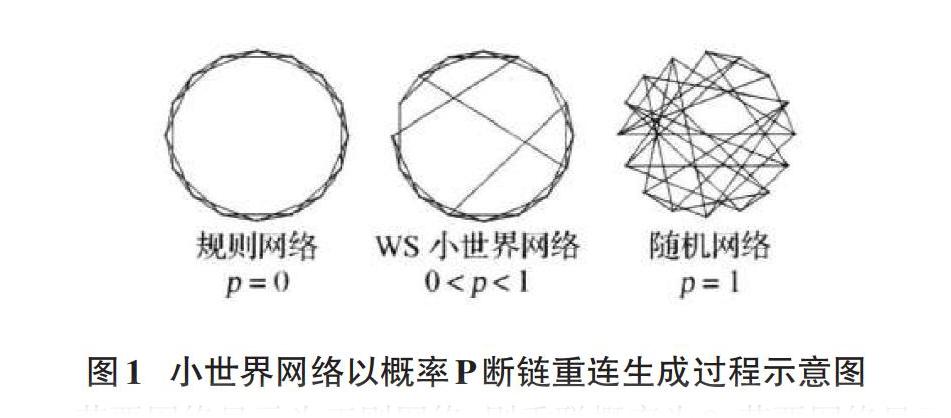
1998年，STROGATZ和WATTS提出了小世界網絡模型（WS模型）[2]。通過和經典模型相的對比，小世界網絡模型可以對很多現實網絡自己組織形成的體系進行解釋。隨著時代的不斷發展，關于該研究的深入程度也在不斷提高，很多的實際考察結果也現實，很多真實網絡包括交通網絡具有的世界特征都是比較小的。小世界網絡模型能夠被定義為：隨著環網規則特別是在具有N個節點的情況下被給定，每個節點對稱地連接到其最近的m個鄰居。然后讓每一個節點都以概率P與其他節點進行重連便得到了小世界網絡。如圖1所示演示了這種重連過程。

若要網絡顯示為正則網絡，則重聯概率為0;若要網絡顯示為隨機網絡，則要求p為1;若要求網絡形成是小世界網絡，則要求p處于特殊區間，也就是0與1之間。網絡可以表示為G=（V，E），其中V代表給定的節點，是一組網絡節點;E表示邊，是網絡節點關系的集合。N為網絡節點數，A=（aij）是相應的鄰接矩陣。對于0，1矩陣A來說，若節點i與節點j相連，而且i不等于j，aij=1就會出現，否則aij=0。

2.2 模型特性分析

①小世界網絡平均路徑長度L和聚集系數C

在常規的網絡中，節點和節點間最小的路徑的平均值是路徑平均長度，同時路徑的平均長度也是對節點分離程度的參數的描述;網絡中全部節點的聚類系數的平均值是聚合系數，是對網絡的容錯性能進行描述和對聚合程度盡心表述的參數[2]。在規則性的網絡中，因為節點是根據特定的條件進行分布的，這種情況下它們的聚集系數C都是比較大的，只是節點和節點間的平均路徑長度L的值也會比較大。隨機網絡因為它們節點的分布都是比較隨意的，所包含的聚集系數一般比較小，以及平均路徑長度L也比較小。作為分布于兩種網絡之間的小世界網絡，使得小世界網絡同時具備這兩種網絡的長處，也就是含有較大的聚集系數C，較小的平均路徑長度L，從而使得小世界網絡具備比較好的網絡特性。

②小世界網絡的效率

為了使得小世界網絡可以被更直接又生動地表現出來，對于引入其他重要的參數效率也是必要的。經過對這個參數的引入，使得小世界網絡的效用能夠被用一個定值表現出來。基于網絡知識和圖論，在描述一個公共網絡的過程中能夠使用兩個矩陣：相互關聯的矩陣（aij）和一階鄰接矩陣（lij）[3]。當點i和點j的邊連通無阻時，aij=1，lij是兩點之間的現實距離;當i點和j點沒有被直接連通時，aij=0，lij=∞。如圖2所示。

在得到aij和lij后，用貝爾曼算法能夠取得最短路徑矩陣dij[3]，并將i點和j點兩點間的效率解釋為eij=1/dij，vi，j，如果dij≤lij，那么i點和j點之間的效率也可以被闡釋為eij=1/dij，vi，j。若dij=∞，那么aij=0，能夠總結出e（g）=[1/（n-1）]1/dij是網絡的平均傳輸效率。理想情況下，它可以被認為是dij=lij，emax=e（g（n，n（n-1）/2）=[1/n（n-1）]1/lij。上面所描述的就是全局效率Eglobe參數[4]，對于完整網絡和現實的網絡在他們之間的平均路徑的對比過程中進行描述，也就是對平均路徑在現實網絡和完整網絡之間到底有多大的相似度，能夠得出0≤e（g）≤1，如果e越接近1，那么效率就會變高。

但是，在實際網絡中，維持每一個節點都可以正常并同時間進行工作的狀態是很難的。如果一個節點在網絡中不能和平常情況一樣進行工，那么對于提高網絡的效率就是必須要做的事情。在對網絡中容錯性尤其是自治分散板塊進行描述時，對另外一個參數進行了定義：局部效率ELOC[4]。如果全局效率gi是除去網絡中i點后的，那么局部效率公式就可以被闡釋為Eloc=1/NΣE（gi）。

3 模型算例

在城市公共交通網絡的建設過程中，其社會性的特點在逐漸的突出，人工規劃城市公共交通網絡的過程中，所受到的影響因素是多方面的。所以，由此看，總線網絡不僅不是完整網絡也不是隨機網絡。從城市交通網絡自身的特性來進行了解，發現較小的世界效應都是經過較小的平均站間和較大的聚集度進行反映的。一些研究表明，公交網絡是一個小型世界網絡，具有通過指數進行分布、明顯的社區結構以及較強的通信能力等特點。

為了對公交線網優化中的小世界網絡的應用進行研究，對杭州市主城區中心區域公交站點和線路組成的網絡進行實例分析。圖3見研究區域的公交站點。

在實例分析中，對現有網絡進行了抽象描述：（1）將每個車站視為網絡中不同的節點;（2）同一條線路作為節點在不同的車站以相同公交站名處理;（3）將公交線路網絡中站點間的連接線視為連接網絡節點之間的弧線;（4）圓弧兩端兩個節點和節點間的距離是對圓弧的權重的表示;（5）孤立的車站不存在于公交網絡中，因為所有的兩個車站都能夠被一條或多條線路進行連接，因此網絡連接是比較完全的。在上述抽象定義的基礎上，通過在杭州主城區中心區布置公交線路和站點，共得到78個節點，即N為78，從而建立了78階距離矩陣。得到了公交網絡的最短路徑矩陣。網絡系統的全局效率和局部效率分別為0.2864和0.4674。所以，當全局和局部之間的效率越來越接近1時，也是網絡整體性能最好的時刻。由于計算結果仍遠未達到預期水平，對目前存在的網絡進行了重新架構，并通過增加和刪除一些總線線路和調整網絡節點進行了改進。優化后，總效率為0.4227，局部效率為0.5324，都有一定的提升。公交線網優化的流程圖見圖4。

4 結論與展望

公交線網優化是系統工程，需要循環往復的進行優化，從而使得在公交線網優化中使用小世界理論給出最直接的參考依據。但是根據本研究所提方法對現有公交線網進行調整涉及方方面面的復雜因素，不一定能起到立竿見影的效果，最多可以給城市交通的管理者提供具有限制的參考價值，因此本研究方法比較適用于新建公交網絡的設計。另外在規模較大線網系統中，建立矩陣和計算需要大量的工作量，也可通過對線網系統進行適當分塊來解決，怎么樣將規模比較大的線網系統進行合理的優化和劃分還需要進行深入的探討。

參考文獻：

[1] Christos Valouxis，EfthymiosHousos.Combined bus and driver scheduling.Computer& Operations Research 29，2002：243-259.

[2] WATTS D J， STROGATEZ S H.Collective dynamics of small-world netword[J].Nature，1998，3（5）：393-440.

[3] 樊夢.基于WS小世界網絡拓撲特性的自組織PSO算法[J].大眾科技，2010（10）：35-37.

[4] 汪小帆，李翔，陳關榮.復雜網絡理論及其應用[M].北京：清華大學出版社，2006.

[5] 史路.城市公共交通線路模擬優化[J].公路交通技術，2014（04）：111-118.

【通聯編輯：王力】