最優(yōu)化原理在動態(tài)規(guī)劃中的應(yīng)用

日毛吉,張愛萍

(1.西北民族大學(xué) 數(shù)學(xué)與計算機科學(xué)學(xué)院,甘肅 蘭州 730030；2.城關(guān)區(qū)教師進修學(xué)校附設(shè)小學(xué)，甘肅 蘭州 730030)

1 引言

動態(tài)規(guī)劃主要是按照系統(tǒng)狀態(tài)而進行時間與空間上的階段性控制，并運用數(shù)學(xué)方法對各個階段的狀態(tài)進行推算，并做出最終最具實效性、最佳經(jīng)濟效益的決策[2].在經(jīng)濟發(fā)展的不斷推動下，各行各業(yè)的生產(chǎn)經(jīng)營活動的擴張，增加了資金管理、資源管理、能源管理、人力資源管理、公共事業(yè)管理等的復(fù)雜程度，給管理科學(xué)提出了許多新的要求與問題，數(shù)學(xué)作為管理科學(xué)中數(shù)量分析方法的基礎(chǔ)，解決這些問題具有獨特的思路和方法，其中動態(tài)規(guī)劃的思想方法顯著的效果得到了廣泛的應(yīng)用[8,10].因為動態(tài)規(guī)劃的方法在處理某些比較復(fù)雜的問題進行優(yōu)化時，比整數(shù)規(guī)劃、目標(biāo)規(guī)劃，線性規(guī)劃和非線性規(guī)劃等用動態(tài)規(guī)劃比其他方法更方便求解.但實施動態(tài)規(guī)劃需要充足的資金支持和對管理系統(tǒng)進行維護，不僅對系統(tǒng)維護人員和維護費用都需要資金的支持，還要有充足的人力、資金和物質(zhì)來保障的條件下才能有效進行.動態(tài)規(guī)劃管理在企業(yè)發(fā)展和市場競爭力的提高中起著重要的作用，它可以優(yōu)化企業(yè)的管理過程，為企業(yè)的發(fā)展帶來重要的保障[1].

動態(tài)規(guī)劃最初是由理查德·貝爾曼(Richard Bellman)在20世紀(jì)40年代提出的，是為了敘述并處理某一些比較特殊問題的過程，所以在該過程中不時地尋找最優(yōu)的決策方案.到1953年，Bellman繼續(xù)對動態(tài)規(guī)劃問題進行了推理分析，著重提出動態(tài)規(guī)劃的作用是在較大的決策中代入較小的決策問題.1957年Bellman發(fā)表了很多學(xué)術(shù)論文，并出版了他的第一部著作《動態(tài)規(guī)劃》，這本書成為當(dāng)時應(yīng)用和研究動態(tài)規(guī)劃理論的唯一書籍.在Bellman與協(xié)助他的工作人員正在完善和推廣此方法的同時，在時刻關(guān)注動態(tài)規(guī)劃發(fā)展的其他的一些學(xué)者也對此做出了很大的功績，其中貢獻最大的是Aris和Mitten.Aris在三年期間共出版了兩部涉及動態(tài)規(guī)劃的著作，并在1964年與Wild.

Nemhauser聯(lián)手創(chuàng)立了解決分枝、循環(huán)性多階段決策系統(tǒng)的一套理論.

自從動態(tài)規(guī)劃在我國應(yīng)用開始，很多學(xué)者對動態(tài)規(guī)劃進行了詳細(xì)的研究，2014年趙娟、樊超[3]對動態(tài)規(guī)劃的使用方法進行了詳細(xì)的描述；2015年梁聰剛、王鴻章[9]對供應(yīng)鏈與排序問題在動態(tài)規(guī)劃的背景下進行研究；2014年潘云濤[6]將動態(tài)規(guī)劃與公共設(shè)施管理聯(lián)系在一起進行研究.2015年程六滿、王柯敬[11]闡述了各行各業(yè)的企業(yè)都在管理應(yīng)用中加入取得到了廣泛的應(yīng)用.常淑芬[7]通過實際管理中的一些例子來闡述動態(tài)規(guī)劃在管理中的應(yīng)用.而Mitten則提出的一些基礎(chǔ)性觀點后來也被應(yīng)用在動態(tài)規(guī)劃的發(fā)展當(dāng)中，并對顯式動態(tài)規(guī)劃路徑的數(shù)學(xué)性質(zhì)做出了很大的貢獻.

2 基本原理

一個過程的最優(yōu)策略具有這樣的性質(zhì)，即無論其初始狀態(tài)及其初始策略如何，其以后諸決策對以第一個決策所形成的狀態(tài)作為初始狀態(tài)而言，必須構(gòu)成最優(yōu)策略[4,5].

基本步驟：

(1)將問題的求解過程恰當(dāng)?shù)胤殖扇舾呻A段，一段可按問題所處的空間或時間進行分，并確定階段變量，對n個階段問題(k=1,2,...,n);

(2)正確地選擇狀態(tài)變量sk，它應(yīng)當(dāng)滿足無后效性等三個條件，并確定狀態(tài)集合sk;

(3)確定決策變量xk及階段的允許決策集合Dk(sk);

(4)寫出狀態(tài)轉(zhuǎn)移函數(shù)sk+1=Tk(sk,xk);

(5)由已知條件，得到指標(biāo)函數(shù)Fk,n,fk(sk),F1,n,f1(s1)由最優(yōu)化原理，列出

fk(sk)={Fk,n(sk)}=min{d(sk,xk)+fk+1,n(sk+1)}.

于是得基本方程

也稱為逆序法遞推公式.

3 模型求解

3.1 逆序解法

由于查找最優(yōu)解優(yōu)方向與多階段決策過程的實際進行方向相反，從最后一段開始計算逐段前推，求得全過程的最優(yōu)策略.

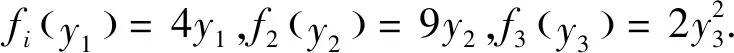
解：令第k階段初已有的狀態(tài)變量sk是分配給第k到第三個項目的金額；決策變量yk為投第k個項目的資金；狀態(tài)轉(zhuǎn)移方程為sk+1=sk-yk.初始狀態(tài)為sk時，從第k到第三個項目的利潤最大，第k階段的最優(yōu)指標(biāo)函數(shù)用gk(sk)表示，那么g1(s1)為所計算的總利潤.

遞推方程為：

k=3時，

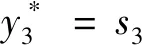
k=2時，

設(shè)

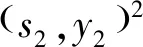
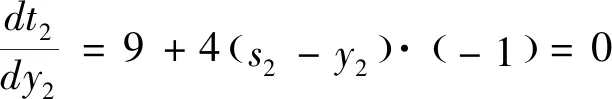
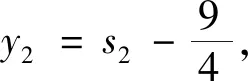
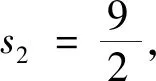
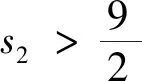
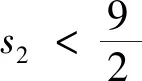
當(dāng)k=1時，

g2(s2)=9s2時，

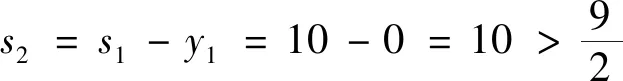
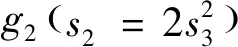
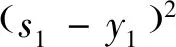
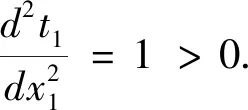
其次，穩(wěn)定供需關(guān)系，健全天然氣需求管理。建立天然氣發(fā)展綜合協(xié)調(diào)機制，推動供用氣企業(yè)全面簽訂合同，鼓勵簽訂中長期的供氣合同。“煤改氣”堅持以氣定改，在落實氣源的前提下有規(guī)劃的推進。突出京津冀及周邊重點區(qū)域，同時建立和完善天然氣領(lǐng)域信用體系，對嚴(yán)重違法失信行為實施聯(lián)合懲戒，健全天然氣供需側(cè)管理，準(zhǔn)確預(yù)測天然氣需求。

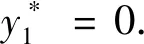
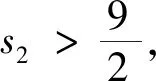
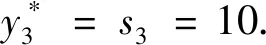
因此，最優(yōu)方案于投資第三個項目，最大利潤為200萬元.

3.2 順序解法

尋優(yōu)方向與過程的行進方向相同，計算時從第一段開始逐段向后遞推，計算后一階段要用到前一段的求優(yōu)結(jié)果，最后一段計算的結(jié)果是全過程的最優(yōu)結(jié)果.

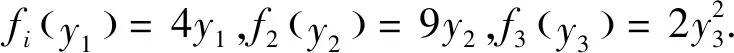
解：設(shè)第1到第k個項目投入的資金用狀態(tài)變量sk+1,那么s4=10,s3=s4-y3,s2=s3-y2.即狀態(tài)轉(zhuǎn)移方程：sk=sk+1-yk,令第k段投入的資金sk+1用最優(yōu)指標(biāo)函數(shù)gk(sk+1)表示，當(dāng)投入的資金sk+1時，獲得第1到第k項目的最大利潤，故可得基本方程為：

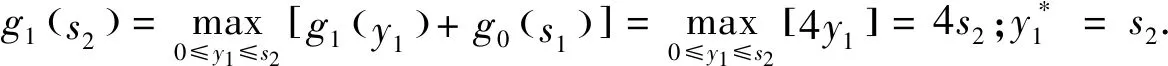
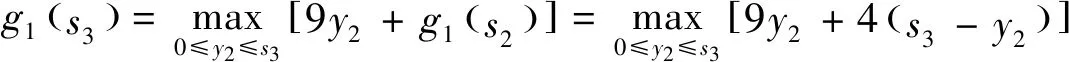
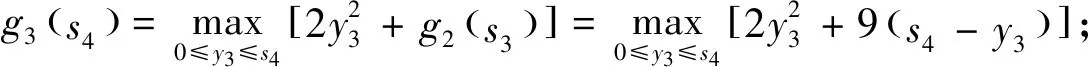
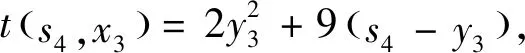
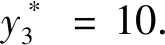
因此，最優(yōu)解與逆序法是相同的，該公司只投資于第三項時才獲得最大利潤200元.

4 應(yīng)用舉例

4.1 資源分配中的應(yīng)用

例3.M集團有5個新設(shè)備，將分配給下屬的三個分公司機構(gòu)，利潤如表1所示.那么，該集團如何分配設(shè)備以實現(xiàn)總利潤最大化.

表1 設(shè)備臺數(shù)及利潤的關(guān)系

分析：管理的目標(biāo)是在最小成本下實現(xiàn)最大利潤，如何獲得有限資源的最優(yōu)配置是項目投資中要考慮的問題.

解：

(1)建立數(shù)學(xué)模型

令第i個分公司收到xi設(shè)備后得到的收益用目標(biāo)函數(shù)Ti表示，分配給第i個分公司的設(shè)備總數(shù)用決策變量xi表示，那么

設(shè)備分配給第k個分公司的過程為第k個階(k=1,2,3),狀態(tài)變量sk為分配給第k個分公司的設(shè)備總數(shù),0≤sk≤5,決策變量xk為分配給第k個分公司的設(shè)備數(shù),0≤xk≤sk,狀態(tài)轉(zhuǎn)移方程：

第k個分公司接受xk設(shè)備后得到的收益用階段目標(biāo)函數(shù)Tk(sk,xk)表示，將設(shè)備sk分配給第k個分公司到第n個分公司后到的總收益用最優(yōu)指標(biāo)函數(shù)gk(xk)表示.從而動態(tài)規(guī)劃的基本方程為：

(2)遞序法求解

變量sk=0,1,…,5,xk=0,1,…,5,k=0,1,…,5.

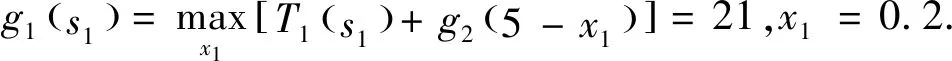
(3)結(jié)論分析

求解得出最大利潤g1(s1)，然后按k=1,k=2,k=3.遞推，從而得出最優(yōu)策略有兩種方案：x1=0,x2=2,x3=3或x1=1,x2=2,x3=1.得到的結(jié)果可知，第三個分公司1臺，分配給第二個和第三個分公司2臺，或分配第一個分公司0臺，第二個分公司2臺設(shè)備，第三個分公司3臺設(shè)備或分配給第一個分公司2臺，該集團的利潤和為21萬元.

4.2 采購與銷售問題中的應(yīng)用

例4.服裝城使用倉庫來專門銷售一種產(chǎn)品.倉庫的最大容量可以儲存1000單位的貨物.如果服裝城每個月只能銷售倉庫月的貨物.該服裝城在某月進貨時，貨物下月初能到，甲商品四個月的買賣價格如表2所示，若服裝城自一月銷售以來，倉庫有商品500單位.該服裝城如何計劃一月至四月的進購與銷售，若不算庫存成本，使預(yù)期收益最大.

表2 買賣價格表

解：(1)變量說明

狀態(tài)變量sk：第k月初倉庫中的存貨量；決策變量xk：第k月賣出的貨物數(shù)量；決策變量yk：第k月訂購的貨物數(shù)量；狀態(tài)轉(zhuǎn)移方程:sk+1=sk+yk-xk;最優(yōu)指標(biāo)函數(shù)fk(sk):從第k月到4月末所獲得的最大收益.則有以下逆序遞推關(guān)系式：

(2)問題求解

x3=s3,y3=1000時,有最大值，f3(s3)=60000+13s3;

得x2=0,y2=10000-s2,f2(s2)=6000+13s2+4000-4x2=10000+9s2;

得x1=500,y1=0,f1(500)=14500+3×500=16000.

表3 最優(yōu)策略表

(3)結(jié)論分析：第一月訂購的貨物數(shù)量為0.賣出的貨物數(shù)量為500時，則由逆序遞推得出最大利潤為16000.

4.3 生產(chǎn)管理中的應(yīng)用

例5.時代設(shè)計公司一個機器設(shè)計出兩種不同價格產(chǎn)品的模型，機器一天內(nèi)可利用8小時，設(shè)計兩種模型的任意一種都要占機器1小時，令兩種模型售價與產(chǎn)量成線性關(guān)系.(10-s1)與(14-2s2)為該兩種產(chǎn)品的銷售價格，而s1,s2分別為兩種產(chǎn)品模型的產(chǎn)量,設(shè)兩種產(chǎn)品的成本分別為2s1和4s2,如何安排兩種產(chǎn)品模型的生產(chǎn)量才能使該電腦在8小時內(nèi)獲收益最大.

解：(1)問題分析：令y1是電腦可利用的，即s1=8,y2是生產(chǎn)第一種產(chǎn)品s1件后剩余的可利用的電腦時間，y3是生產(chǎn)第二種產(chǎn)品s2件后電腦可利用的時間.

(2)建立模型:因要求電腦用8小時，所y3=0.于是狀態(tài)方程為：

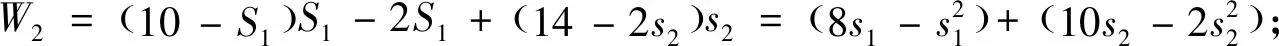
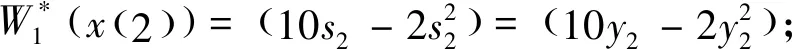
由狀態(tài)方程y2=y1-s1代入上式得：

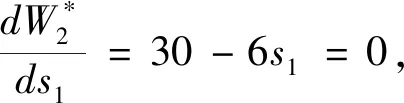
由此得到最優(yōu)策略生產(chǎn)第一種產(chǎn)品模型5件，第二種產(chǎn)品模型3件，8小時可獲收益27百元.

4.4 設(shè)備更新中的應(yīng)用

例6.全自動洗衣機的平均一年的更新凈費以及維修費用、效益表4所示，如何在接下來五年內(nèi)制定更新戰(zhàn)略，以實現(xiàn)總利潤最大化.

表4 更新凈費和維修費、效益用表

解：當(dāng)k=5時，狀態(tài)變量r5可取1,2,3,4

當(dāng)k=4時，狀態(tài)變量r4可取 1,2,3,

當(dāng)k=3時，狀態(tài)變量r3可取1,2,

當(dāng)k=2時，狀態(tài)變量r3只取1,

當(dāng)k=1時，狀態(tài)變量r3只取0，

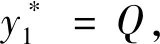
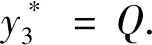
所以最優(yōu)策略為:{K,Q,Q,Q,K},即第一年初購買的全自動洗衣機到第2、3、4初各更新一次，可用到第5年末，總利潤為17千元.

5 結(jié)論

通過對動態(tài)規(guī)劃在管理等方面的應(yīng)用得知，利用動態(tài)規(guī)劃解決某些多階段決策問題，它的思路清晰、簡單、容易實現(xiàn).在一般情況下，將一個大問題拆分成若干個小問題時，利用數(shù)學(xué)算法的方式找到解決每一個分問題的最優(yōu)方法，從而解決一些較大的問題.若在管理的工作中融入動態(tài)規(guī)劃的思想方法，可以為企業(yè)的銷售管理、生產(chǎn)管理、經(jīng)營管理、資源分配等領(lǐng)域的發(fā)展提供有效決策，并且為企業(yè)規(guī)劃人員、處理數(shù)據(jù)和監(jiān)督檢查等部署業(yè)務(wù)做出合理的判斷和分析，更新管理方法和優(yōu)化企業(yè)管理手段，從而提高企業(yè)經(jīng)營各個環(huán)節(jié)的效率和應(yīng)變能力，實現(xiàn)企業(yè)經(jīng)濟效益增長，就會給企業(yè)的管理工作帶來極大的方便.