二叉樹指標隨機場關于分枝馬氏鏈的一類強偏差定理

閔 帆,楊衛國

(江蘇大學理學院,江蘇鎮江212013)

1 引言

本文主要研究二叉樹TC,2(二叉樹TC,2的根點o 與2 個支點相連, 其他的支點與3 個支點相連(見圖1)). 為了方便, 將TC,2簡記為T2. 對于T2上的任一頂點t, 記|t| 表示根點o 和頂點t 之間的距離. 若|t|=n, 則稱t 位于樹的第n 層. Ln表示T2的第n 層上所有頂點的集合, T(n)表示二叉樹T2從0 層(根) 到n 層的所有頂點的子圖. |T(n)| 記為子圖T(n)所含頂點數. 對于二叉樹上任一頂點t, 記t1和t2為t 的兩個子代.

設(?,F) 為一可測空間, {Xt,t ∈T2} 是定義在(?,F) 上且取值于G={0,1,··· ,b ?1}(b 是正整數) 的隨機變量集合, 設B 為T2的子圖, 記XB= {Xt,t ∈B}, xB表示XB的實現. 設P 是可測空間(?,F) 上的概率測度, 我們稱P 為樹T2上的隨機場. 令{Xt,t ∈T2}在P 下的分布為P(XT(n)=xT(n))=P(xT(n)).

定義1.1[二叉樹指標分枝馬氏鏈][1]設T2為二叉樹, {Xt,t ∈T2} 是定義在概率空間(?,F,Q) 上在G = {0,1,··· ,b ?1} (b 是正整數) 中取值的隨機變量集合, 設p ={p(x),x ∈G} 是G 上一概率分布, P = (P(y1,y2|x)) 是定義在G×G2上的一隨機矩陣(滿足P(y1,y2|x)≥0,?x,y1,y2∈G 及如果對n ≥1, 有

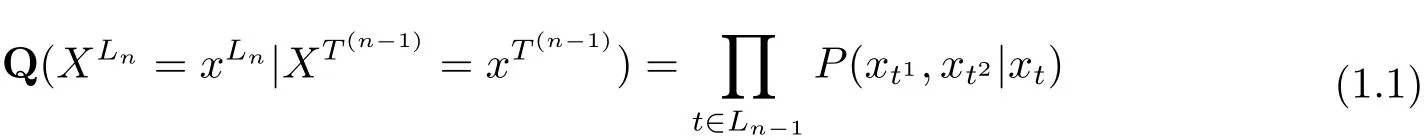
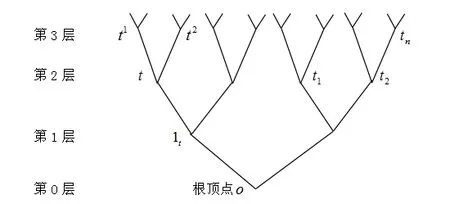
圖1:二叉樹TC,2

及

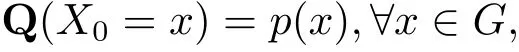
則稱{Xt,t ∈T2} 為具有初始分布p 與隨機矩陣P 并在G 中取值的二叉樹指標分枝馬氏鏈.

注1.2[1]若{Xt,t ∈T2} 在概率測度Q 下為二叉樹指標齊次分枝馬氏鏈, 則

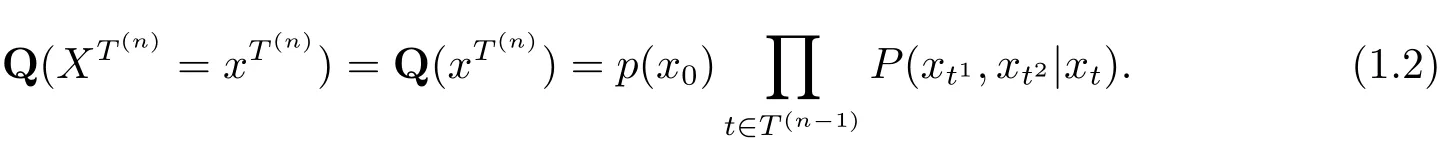
為避免技術問題, 總假定p(x) 和P(y1,y2|x) 是正的.

定義1.3[2]設T2為二叉樹, {Xt,t ∈T2} 是定義在可測空間(?,F) 上取值于G 的隨機變量族, ?x,y1,y2∈G, 設p(x)>0 且P =(P(y1,y2|x)) 為正的隨機矩陣, 設Q,P 為(?,F)上的兩個概率測度, 其中{Xt,t ∈T2} 在概率測度Q 下為具有初始分布p 與隨機矩陣P 的二叉樹指標分枝馬氏鏈. 設P(xT(n))>0, 令

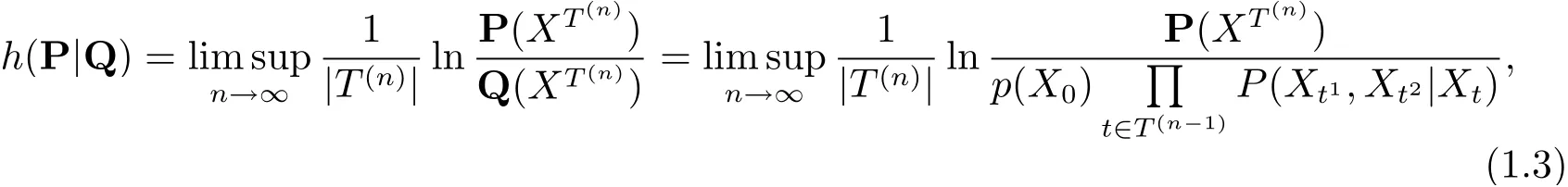
則稱h(P|Q) 為P 關于Q 的樣本相對熵率或漸近對數似然比.

類似于參考文獻[2] 中引理1 的證明可知

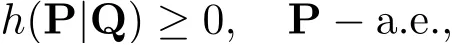
故h(P|Q) 可作為T2上的任意隨機場與分枝馬氏鏈之間偏差的一種度量.

樹指標隨機過程是近年來發展起來的概率論的一個新的研究方向. 文獻[1] 研究了二叉樹上分枝馬氏鏈的等價性質; 文獻[3] 研究了二叉樹有限狀態分枝馬氏鏈的強大數定律和Shannon-McMillan 定理; 文獻[4] 研究了二叉樹上有限狀態分枝馬氏鏈的強大數定理; 文獻[5] 研究了二叉樹非齊次分枝馬氏鏈的等價定義、強大數定理和熵遍歷定理; 文獻[6] 研究了關于齊次樹上隨機場的一類強偏差定理; 文獻[2] 研究了關于Cayley 樹上任意隨機場和馬氏鏈場的強偏差定理; 文獻[7] 研究了齊次樹指標齊次馬氏鏈隨機場的一類強偏差定理; 文獻[8] 研究了Bethe 樹指標隨機場關于非齊次馬氏鏈的一類強偏差定理.

本文通過引入漸近對數似然比作為二叉樹指標任意隨機場與分枝馬氏鏈之間偏差的一種度量, 進而構造鞅的方法, 得出了二叉樹指標隨機場關于分枝馬氏鏈的一類強偏差定理, 作為推論得到了二叉樹指標分枝馬氏鏈的強大數定理和漸近均分性.

2 強偏差定理

強偏差定理是由不等式表示的一類強極限定理, 是由等式表示的一類強極限定理的推廣.本節將建立二叉樹指標任意隨機場關于分枝馬氏鏈的一類強偏差定理.

引理2.1設T2為二叉樹, {Xt,t ∈T2} 是定義在可測空間(?,F) 上的隨機變量族. P與Q 是(?,F) 上的兩個概率測度, 其中{Xt,t ∈T2} 在Q 下是具有嚴格正的隨機矩陣P =(P(y1,y2|x)) 的二叉樹指標分枝馬氏鏈. P(XT(n))>0, 設{gt(x,y1,y2),t ∈T2} 是定義在G3上的函數族, L0={0}, Fn=σ(XT(n)), n ≥1, 令

其中λ 為實數, EQ表示在Q 下的數學期望, 則{tn(λ,ω),Fn,n ≥1} 為在概率測度P 下的非負鞅.

證由式(1.1), (2.1) 可知

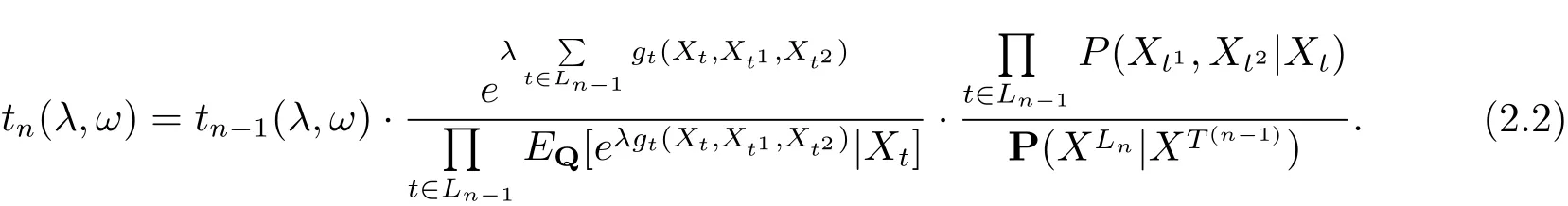
令

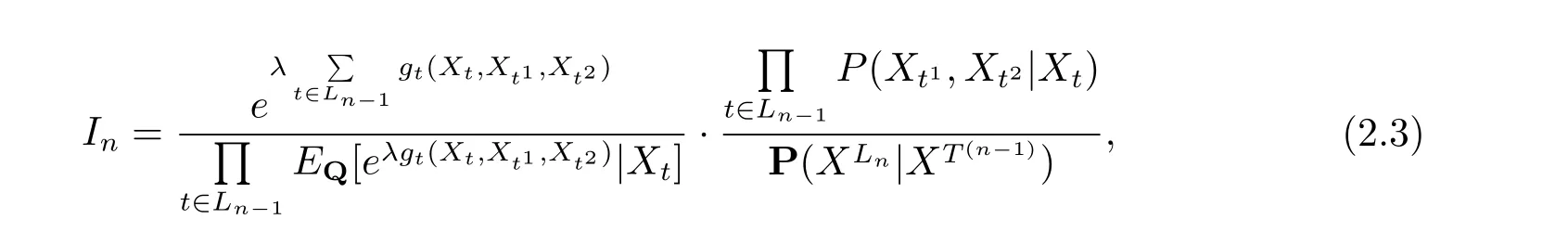
則

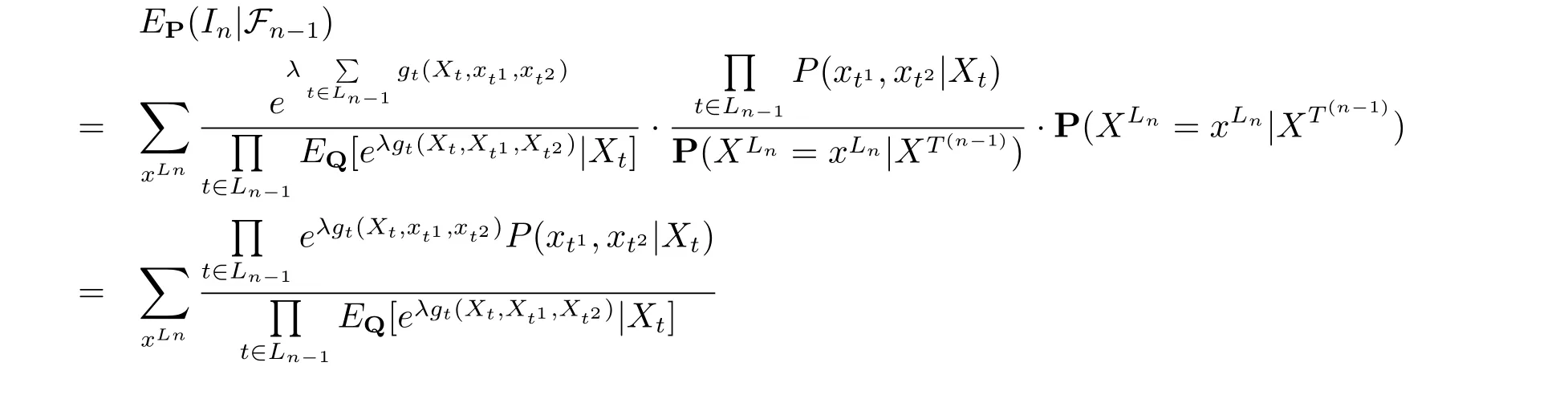
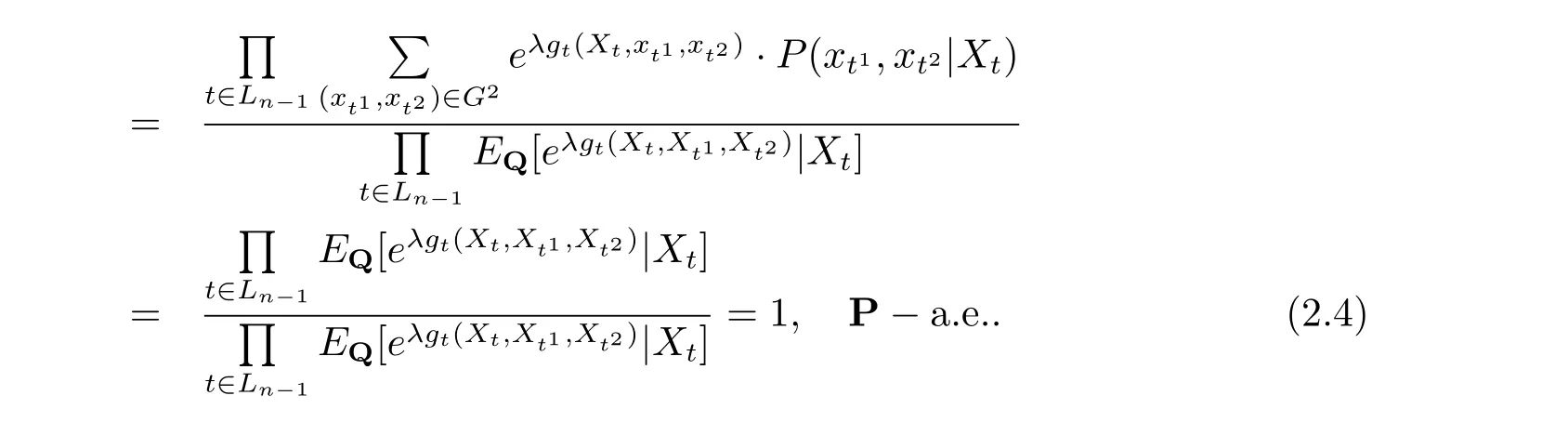
由式(2.2), (2.4) 可知

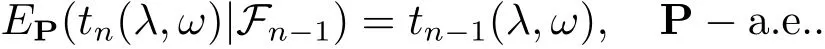
又易知EP[t1(λ,ω)]=1, 因此

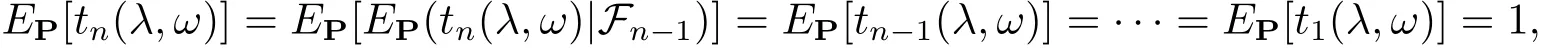
故{tn(λ,ω),Fn,n ≥1} 為在概率測度P 下的非負鞅.

引理2.2設T2為二叉樹, {Xt,t ∈T2} 為二叉樹指標分枝馬氏鏈, 設{gt(x,y1,y2),t ∈T2} 是定義在G3上的函數族, {an,n ≥1} 為正隨機變量序列. 設α>0,

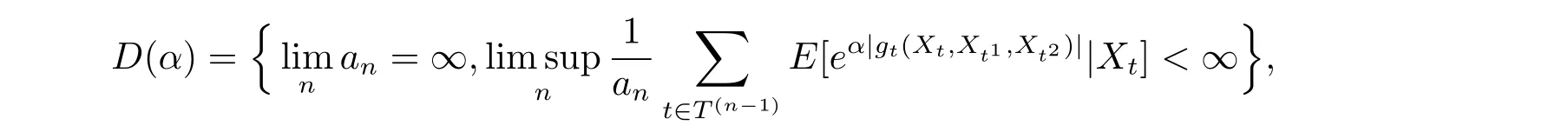
則

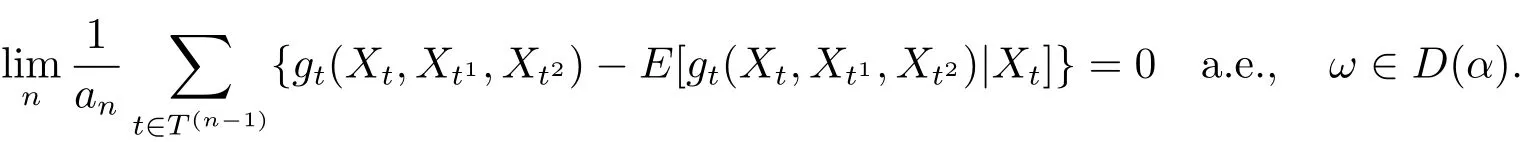
定理2.3設T2為二叉樹, {Xt,t ∈T2} 為定義在可測空間(?,F) 上且取值于G ={0,1,··· ,b ?1}(b 是正整數) 的隨機變量族, P 與Q 是定義在F 上的兩個概率測度, 并且{Xt,t ∈T2} 是在概率測度Q 下的二叉樹指標分枝馬氏鏈, 也即式(1.2) 成立. 令h(P|Q) 如(1.3) 式定義, 且{gt(x,y1,y2),t ∈T2} 是定義在G3上的函數族. 設c ≥0 是一個常數, 令

假設存在α>0, ?i ∈G, 有

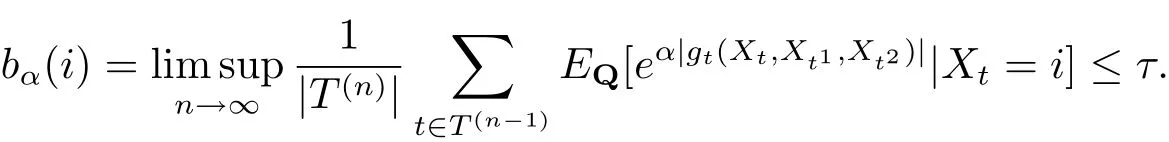
令

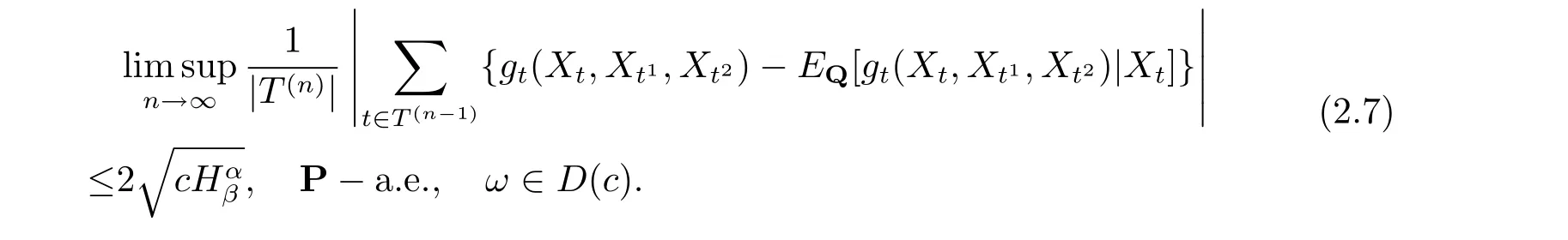
特別地, 有

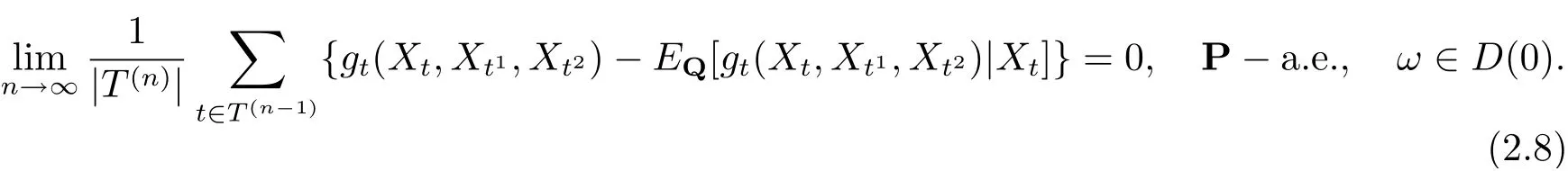
證令tn(λ,ω) 如(2.1) 式定義. 由引理2.1 知, {tn(λ,ω),Fn,n ≥1} 是非負P - 鞅. 則由Doob 鞅收斂定理可知

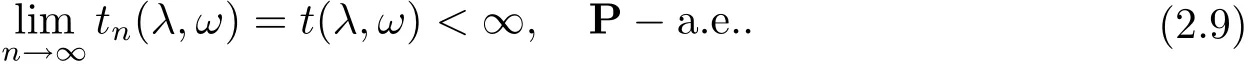
因此有

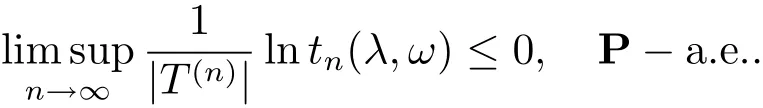
由式(2.1), (2.9) 可知

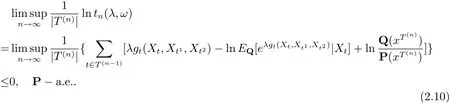
由式(1.3) 及(2.10) 可知

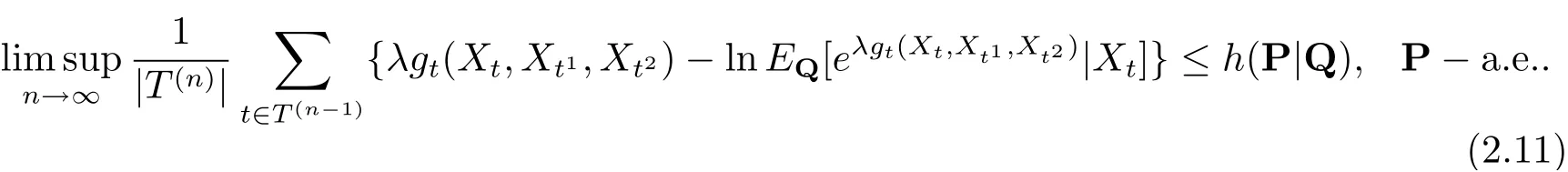
由式(2.11) 可知

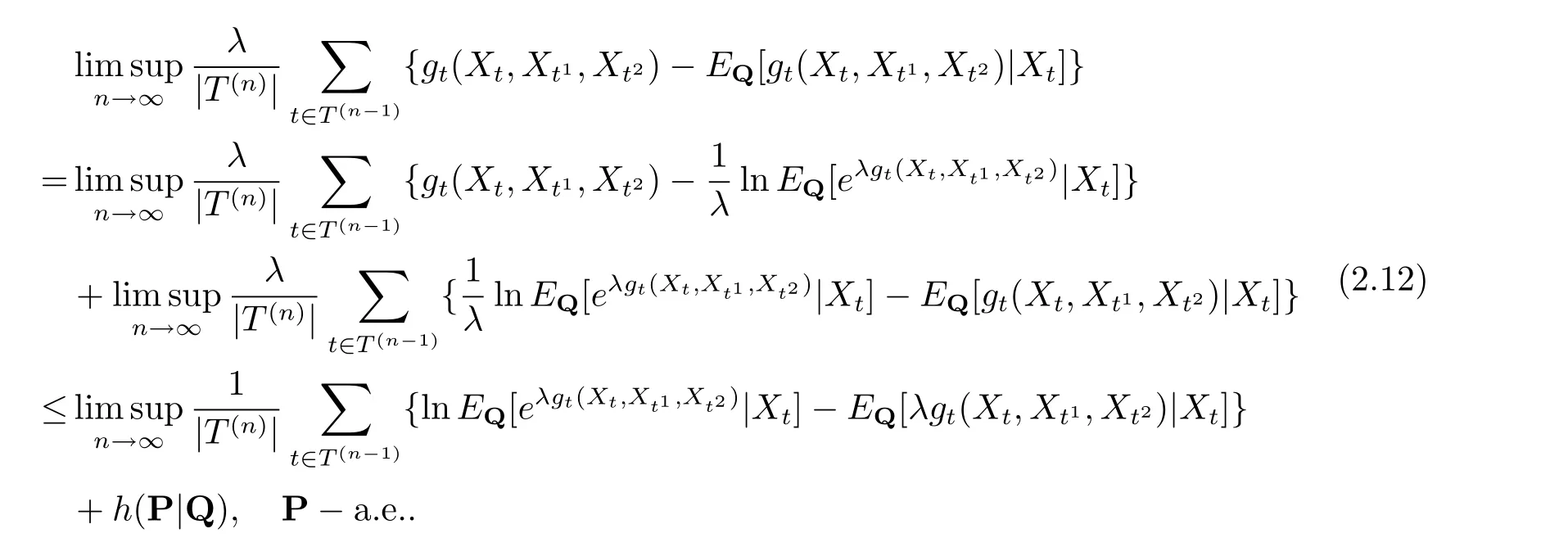
令|λ|≤β. 由不等式ln x ≤x ?1 (x>0) 和并注意到

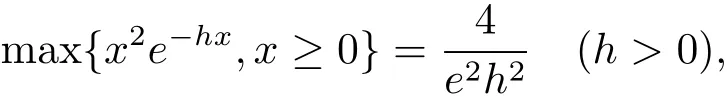
則對于所有的ω ∈?, 有

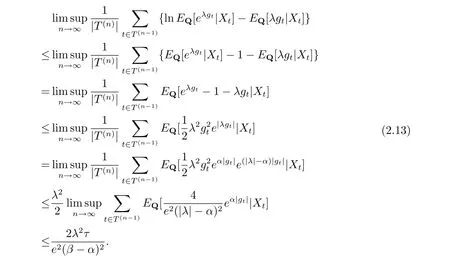
其中為了方便, 將用gt代替gt(Xt,Xt1,Xt2), 由式(2.6), (2.12) 和(2.13) 知

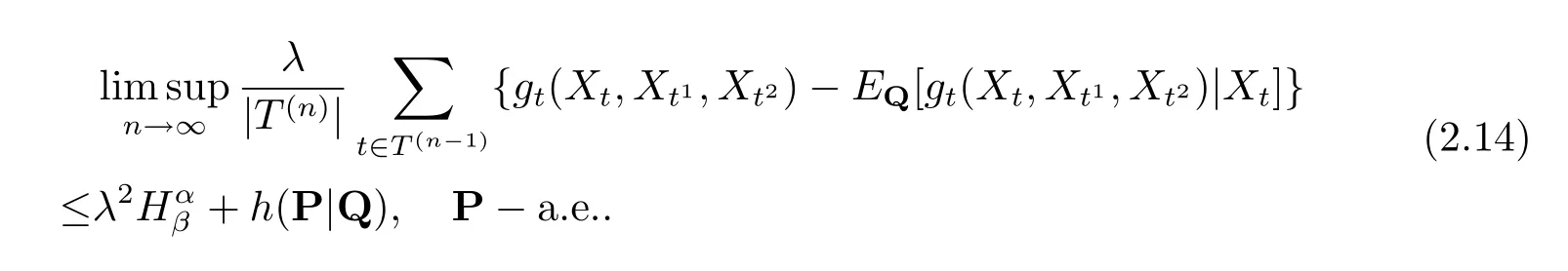
由式(2.5) 與(2.14) 可知

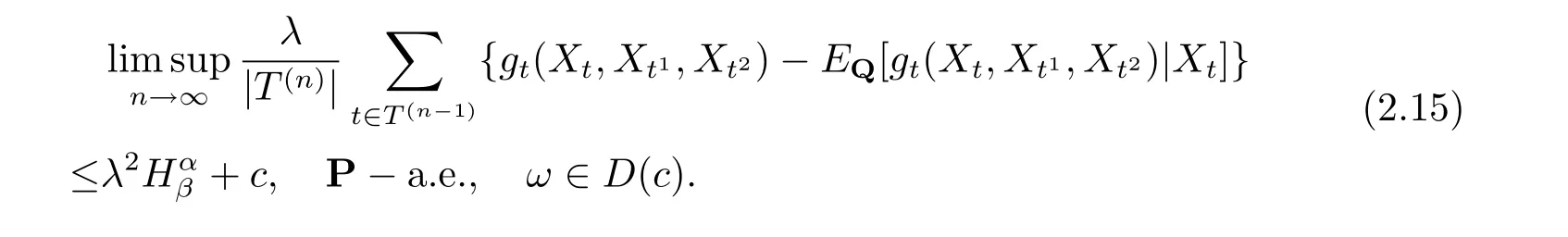
當0<λ ≤β <α 時, 將式(2.15) 左右兩邊同時除以λ 可知

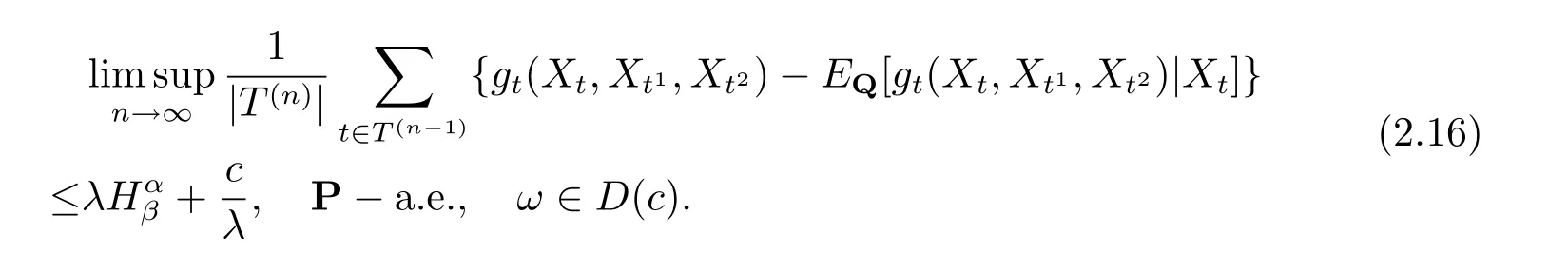
容易看出, 當0 < c < β2Hαβ時, 函數時獲得最小值可知

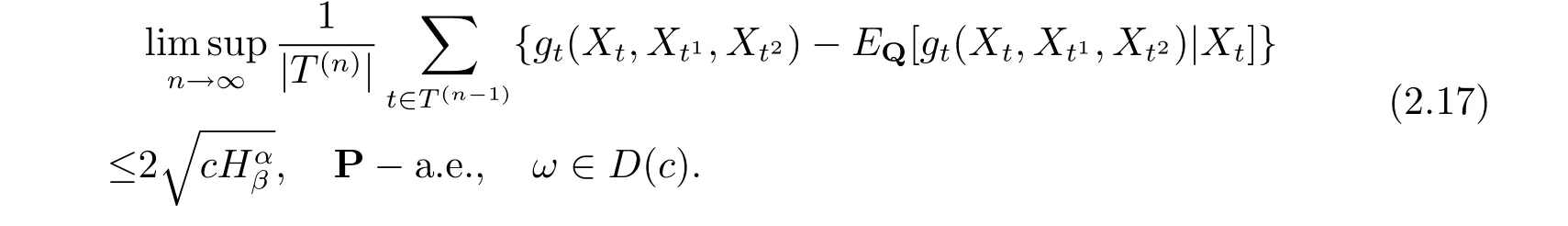
當c=0, 由式(2.16) 可知

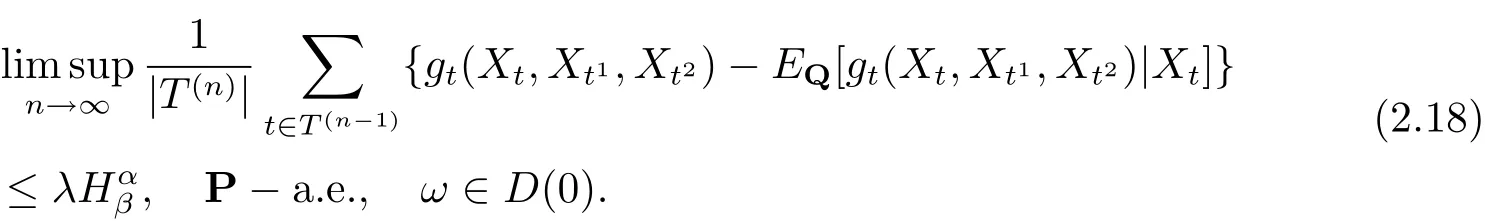
令式(2.18) 中λ →0+, 可知

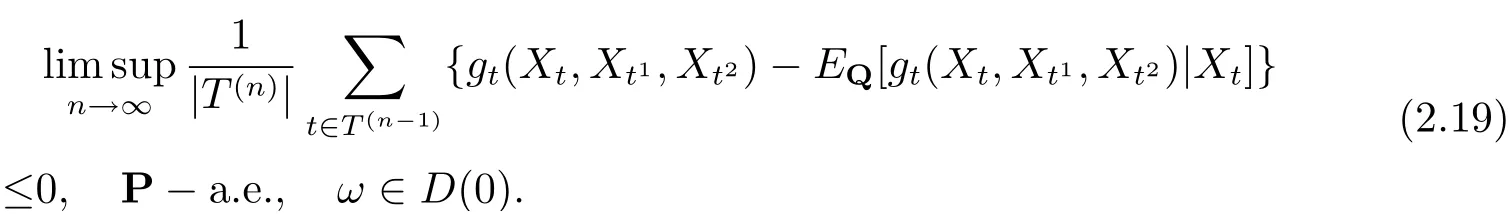
因此當c=0 時, 公式(2.17) 成立. 當?α

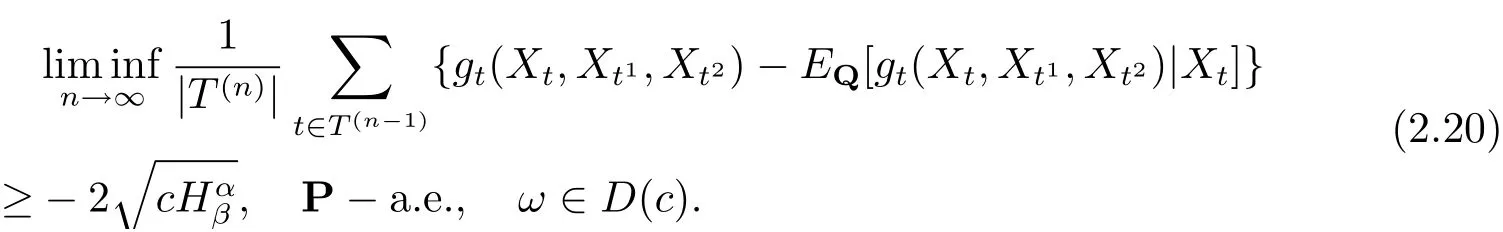
由式(2.17), (2.20) 可知式(2.7), 繼而可知式(2.8). 故此定理2.3 得證.

3 強大數定理及漸近均分性(AEP)

本節研究二叉樹指標隨機場關于分枝馬氏鏈的強大數定理與漸近均分性(AEP), 作為推論得到了二叉樹指標分枝馬氏鏈的強大數定理和漸近均分性.

設T2為二叉樹, {Xt,t ∈T2} 是定義在可測空間(?,F) 上在G 中取值的隨機變量族, 可得結論如下.

定義3.1[3]設P 是(?,F) 上的一個概率測度, xT(n)為XT(n)的實現. 記{Xt,t ∈T2}在概率測度P 下的分布為P(XT(n)=xT(n))=P(xT(n))>0. 設

則稱fn(ω) 為XT(n)在概率測度P 下的熵密度. 如果{Xt,t ∈T2} 在概率測度Q 下是具有初始分布p(x) 和隨機矩陣P 的二叉樹指標分枝馬氏鏈, 則

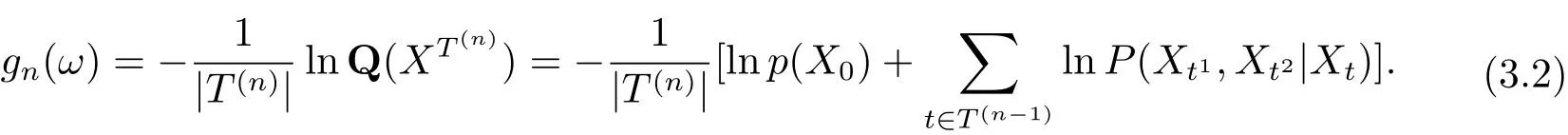
熵密度fn(ω) 收斂(L1收斂, 依概率收斂, a.e. 收斂) 到一個常數的性質在信息論中被稱為漸近均分性(AEP) 或者是Shannon-McMillan 定理.

定義3.2[3]設Sk(T(n))(k ∈G) 是隨機變量集{Xt,t ∈T(n)} 中k 出現的次數,Sn(k,l1,l2) = Sk,l1,l2(T(n)) 是隨機序偶集{(Xt,Xt1,Xt2),t ∈T(n?1)} 中序偶(k,l1,l2)(k,l1,l2∈G) 出現的次數, 即

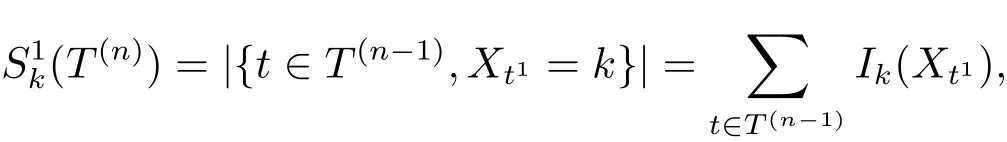
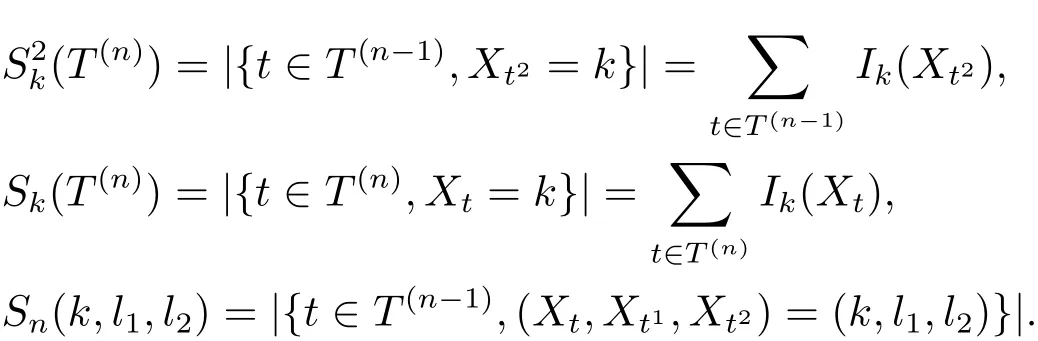
顯然

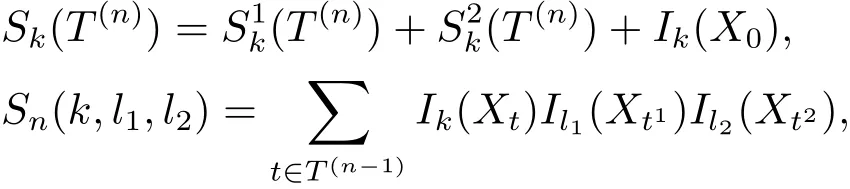
定理3.3設P 與Q 是定義在F 上的兩個概率測度, 并且{Xt,t ∈T2} 是由定義1.1 定義的二叉樹指標分枝馬氏鏈如定義3.2 所定義, 令

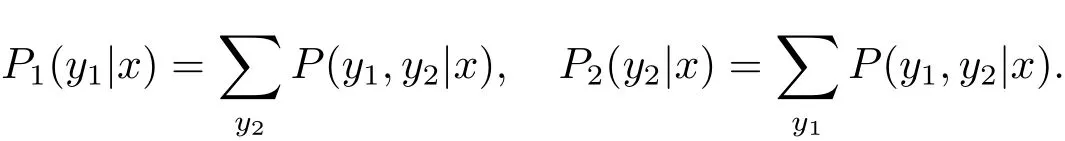
設轉移矩陣P1=(P1(y1|x)),P2=(P2(y2|x)), 令轉移矩陣則

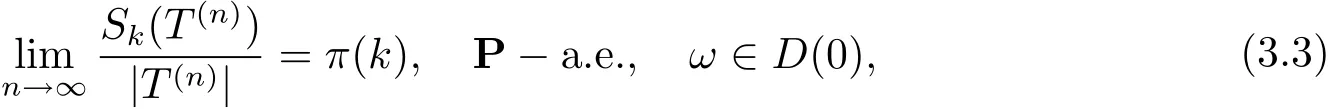
其中(π(0),··· ,π(b ?1)) 為由矩陣R 決定的平穩分布.

證首先轉移矩陣是遍歷的, 這是因為P(y1,y2|x)>0, 可知P1(y1|x)>, 所以. 即R 是遍歷的.

令gt(x,y1,y2)=Ik(y1), 則

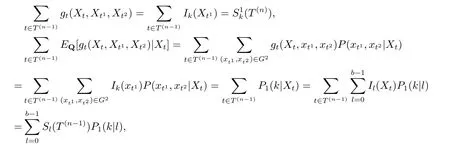
故由式(2.8) 可知

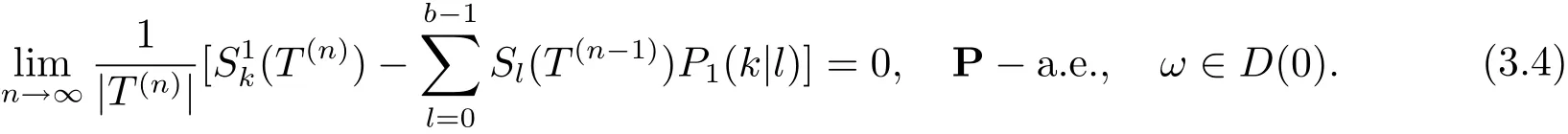
同理令gt(x,y1,y2)=Ik(y2). 類似可知

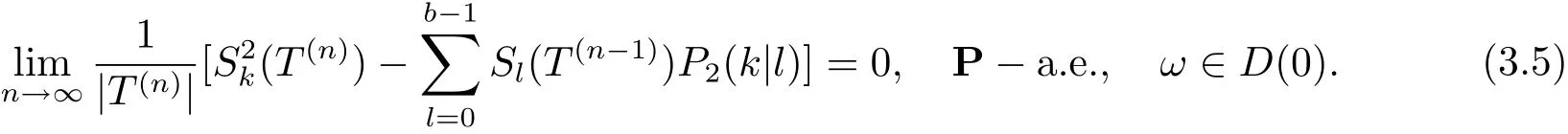
用R(m|k) 乘以式(3.7), 將對k ∈{0,1··· ,b ?1} 求和, 并再次利用式(3.7) 可知

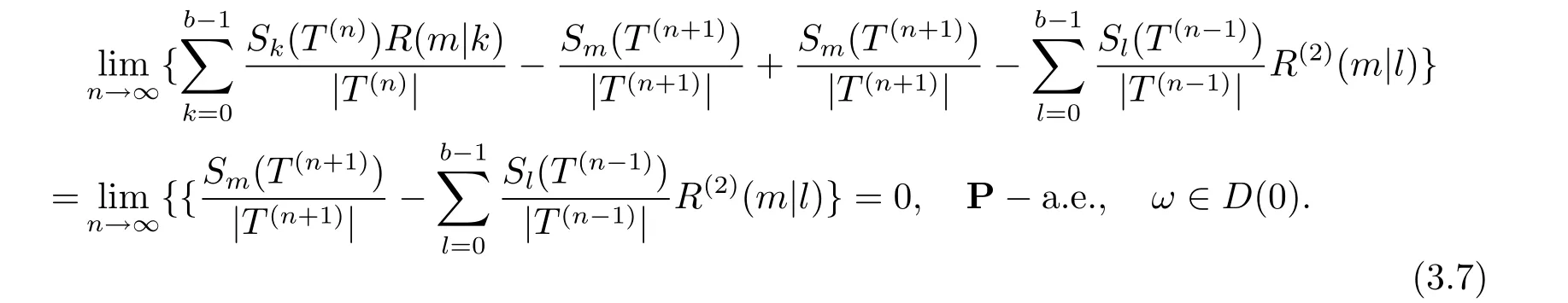
由歸納法可知

注意到

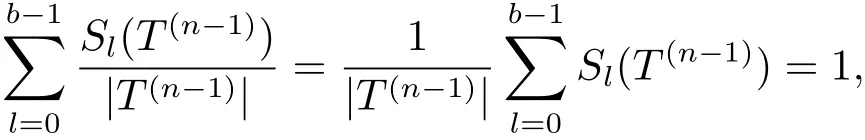
定理3.4在定理3.3 的條件下, 令如定義3.2 所述, 則

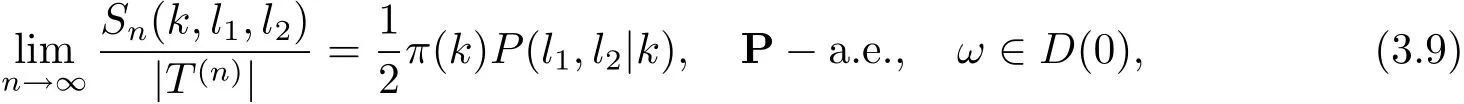
其中(π(0),··· ,π(b ?1)) 為由矩陣R 決定的平穩分布.

證令則

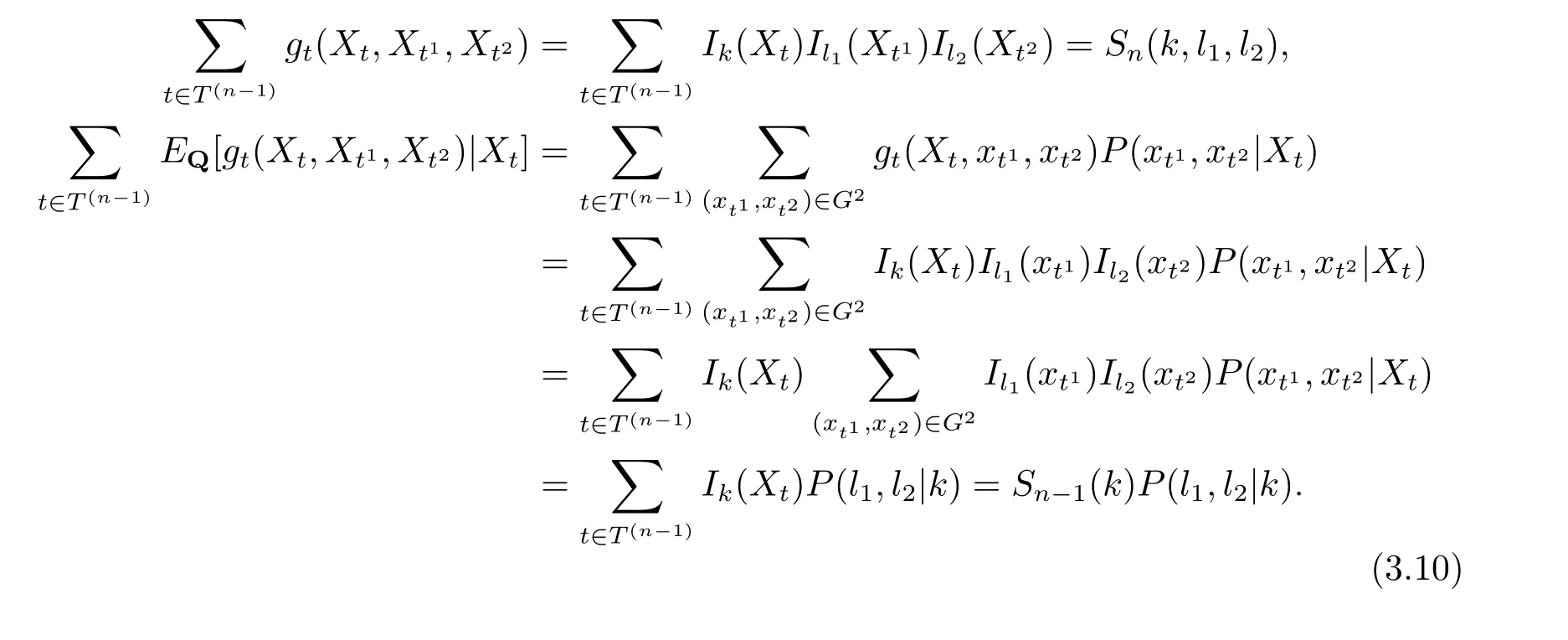
由式(2.8) 可知

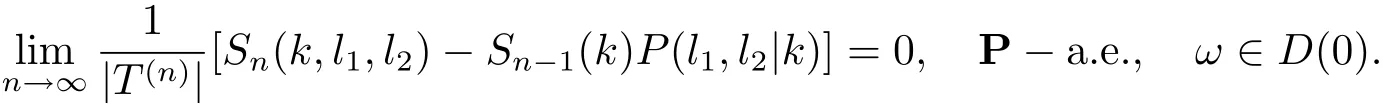
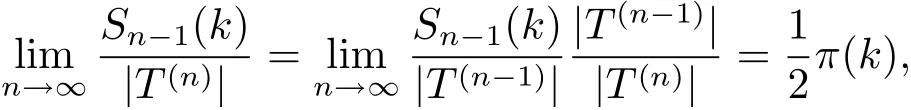
因此式(3.10) 得證.

定理3.5在定理3.3 的條件下, fn(ω) 是如(3.1) 所定義的熵密度, 則

其中(π(0),··· ,π(b ?1)) 為由矩陣R 決定的平穩分布.

證因為

由式(3.2) 與式(3.10)、(3.13) 可知

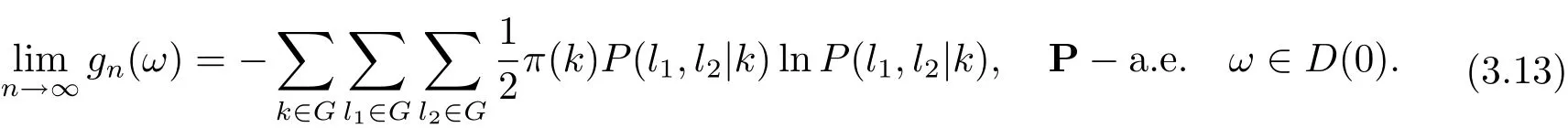
由式(1.3), (3.1), (3.2) 可知

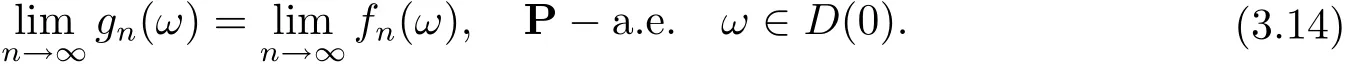
故綜合式(3.14), (3.15) 可知式(3.12) 得證.

定理3.6設{Xt,t ∈T2} 在概率測度Q 下是具有嚴格正的隨機矩陣P =(P(y1,y2|x))的二叉樹指標分枝馬氏鏈, {Xt,t ∈T2},Sn(k),Sn(k,l1,l2), fn(ω) 如定義3.2 所述, 令

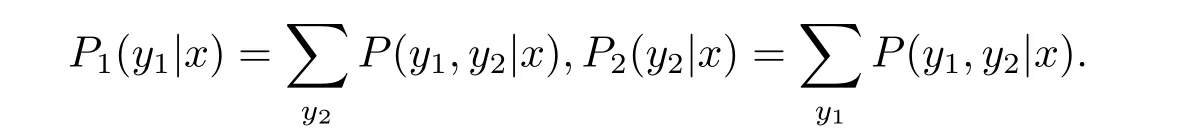
設轉移矩陣P1=(P1(y1|x))P2=(P2(y2|x)), 假設轉移矩陣則

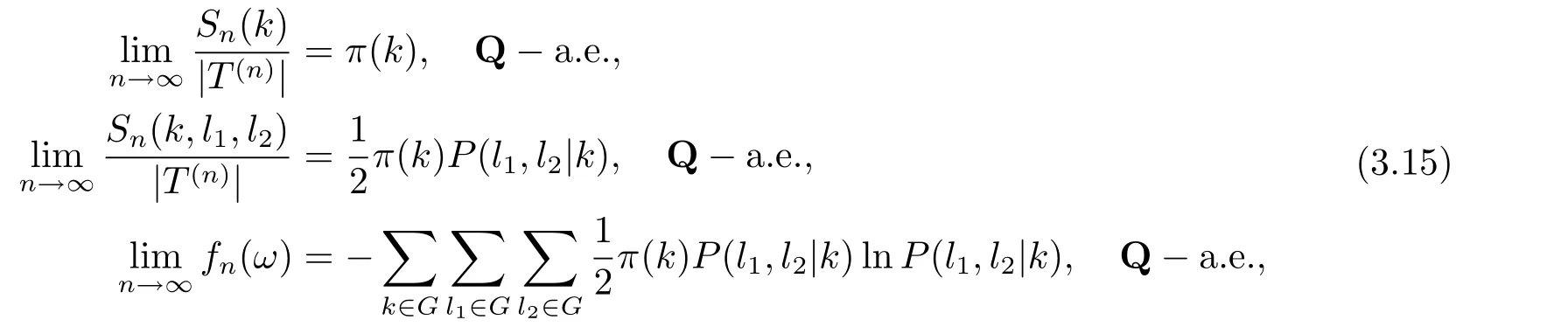
其中(π(0),··· ,π(b ?1)) 為由矩陣R 決定的平穩分布.

證令定理3.3 中P ≡Q, 則gn(ω)=fn(ω), 進而知D(0)=?. 因此由式(3.4), (3.10),(3.12) 可知式(3.16), (3.17), (3.18) 得證.