關于Hayman 問題的差分模擬的值分布

王鑫鑫, 葉亞盛

(上海理工大學理學院, 上海200093)

1 引言

本文采用常用的Nevanlinna 理論的標準記號和基本結果[1?2]. 特別地, λ 表示為f(z)的級, σ2(f) 表示為f(z)的超級. 本世紀, 隨著亞純函數差分模擬的值分布理論的建立[3?4], 國內外學者做了大量的研究, 得到了很多的研究成果[5?8]. 特別, 值分布論中的一些經典結果也被相應的差分模擬. 通常, 平移差分?cf(z)=f(z+c)?f(z) 被看作是的差分對應,f(z)n?cf(z) 和f(z)n+a?cf(z)被看作是微分多項式和f(z)n+a的差分對應. 1959 年, Hayman[9]證明了如下的兩個定理.

定理A設f(z) 為超越亞純函數, n 為正整數, b 為非零有窮復數, 則n ≥3 時,有無窮多個零點.

定理B設f(z) 為超越亞純函數, n 為正整數, a(0) 和b 為兩個有窮復數, 則n ≥5時,+af(z)n?b 有無窮多個零點.

后來, Ye 和Fang 等人[10?11]將定理B 中的f 和交換位置, 得到了下面的定理C.

定理C設f(z) 為超越亞純函數, n 為正整數, a(0) 和b 為兩個有窮復數, 則n ≥2時, f(z)+a?b 有無窮多個零點.

2011 年, Liu[12]等人對定理A 中的f(z)n進行差分模擬, 得到了下面的定理D.

定理D設f(z) 為有限級超越亞純函數, c 為非零復常數, n 為正整數, α(z) 為f(z) 的小函數, 則n ≥6 時, f(z)nf(z+c)?α(z) 有無窮多個零點.

2014 年, Li[13]等人得到了更為細致的定理E.

定理E設f(z) 為有限級超越亞純函數, c 為非零復常數, n 為正整數, 多項式p(z)則

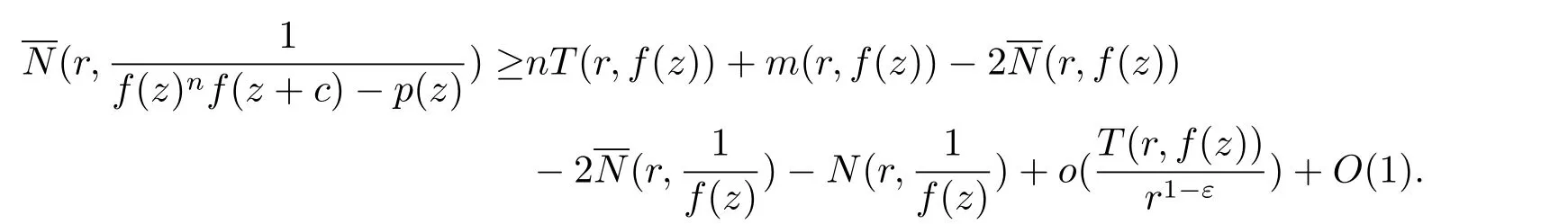
本文主要研究了下面的問題.

(i) 若將定理E 中的f(z+c) 改為f(z) 的差分多項式, 可以得到怎樣的結論？

注1.1 亞純函數f(z) 的差分多項式H(z,f) 定義如下

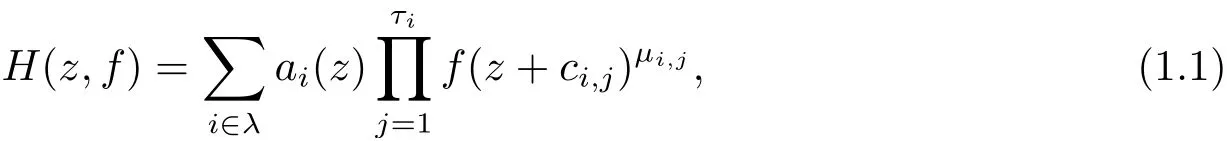
其中λ 為指標集,包含m(≥1)個不同的i,ci,j為復常數,μi,j為非負整數,系數為f(z)的小函數,對H(z,f)的每一個單項式定義其次數為再將H(z,f) 所有單項式的最高次數定義為H(z,f) 的次數, 即

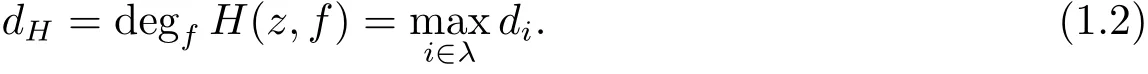
對于問題(i), 首先在一般差分多項式的情況下, 證明了定理1.1.

定理1.1設f(z) 為超越亞純函數, σ2(f)<1, c 為非零復常數, n 為正整數,為f(z) 的小函數, H(z,f) 是形如(1.1) 式的差分多項式, 則

其次, 對比定理E, 下述推論1.1 顯著改進了其結果.

推論1.1設f(z) 為超越亞純函數, σ2(f)<1, c 為非零復常數, n 為正整數,為f(z) 的小函數, 則

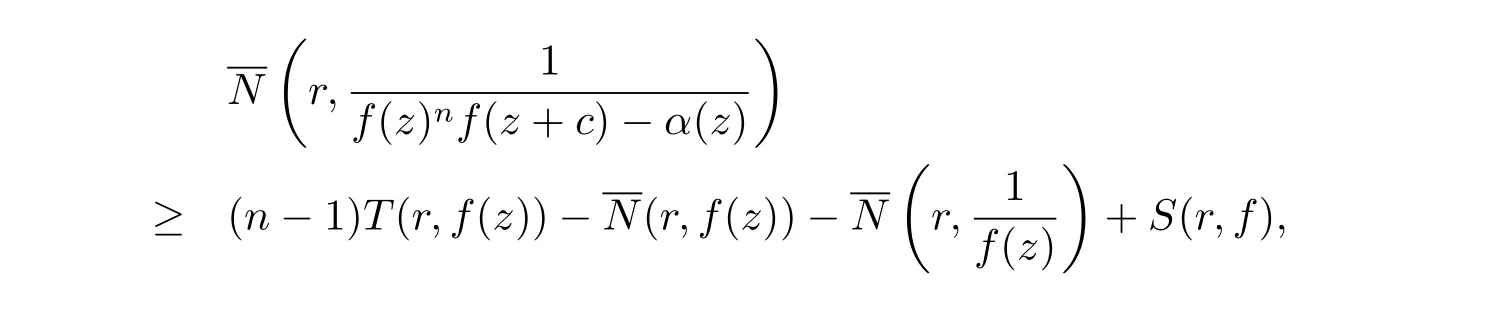
其中r →∞, r /∈E, E 為一個有限測度集.

推論1.2設f(z) 為超越亞純函數, σ2(f)<1, c 為非零復常數, n 為正整數,為f(z) 的小函數, 則n ≥4 時, f(z)nf(z+c)?α(z) 有無窮多個零點.

上述推論1.2 將定理D 的條件n ≥6 改進為n ≥4. 例1.1 說明該結論最佳, 不能再改進.

例1.1f(z)=c=πi, 則當n= 2、3 時,

定理1.2設f(z) 為超越亞純函數, σ2(f) < 1, 且滿足N(r,f) = S(r,f), c 為非零復常數, n 為正整數,為f(z) 的小函數, H(z,f) 是形如(1.1) 式的差分多項式, 且H(z,f) 中僅有一個單項式具有最高次數, 則

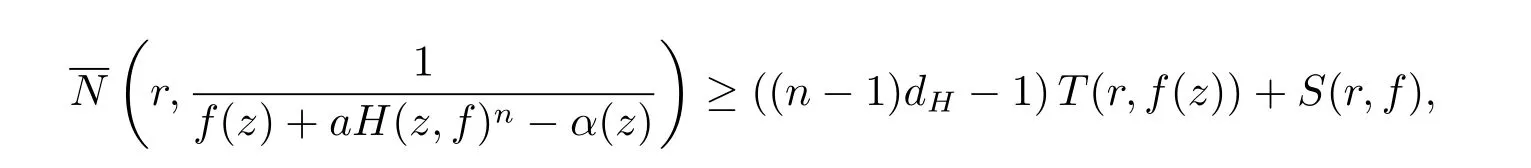
例1.2H(z,f)=f(z)f(z+πi), 則

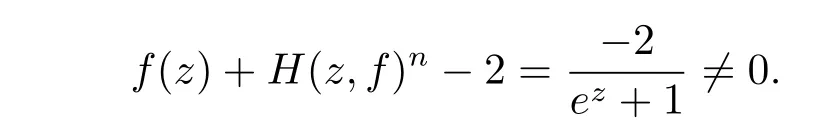
上例說明定理1.2 的條件N(r,f)=S(r,f) 不可缺.

推論1.3設f(z) 為超越整函數, 則n ≥3 時, f(z)+af(z+c)n?α(z) 有無窮多個零點.

例1.3

上例說明推論1.3 結論最佳, 不能再改進.

定理1.3設f(z) 為超越亞純函數, σ2(f)<1, c 為非零復常數, n 為正整數,為f(z) 的小函數, 若f(z) 滿足

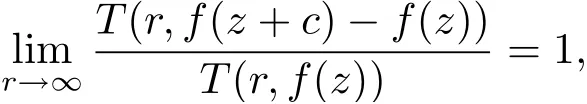
則n ≥5 時, f(z)+a(f(z+c)?f(z))n?α(z) 有無窮多個零點.

例1.4f(z)=ez+p(z), p(z) 為多項式, c=2πi, α(z)=p(z)+(p(z+c)?p(z))n, 則

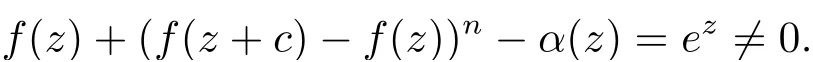
上例1.4 說明定理1.3 若要成立, 需對f(z+c)?f(z) 附加一些條件.

定理1.4設f(z) 為超越亞純函數, σ2(f)<1, c 為非零復常數, n 為正整數,為f(z) 的小函數, 則

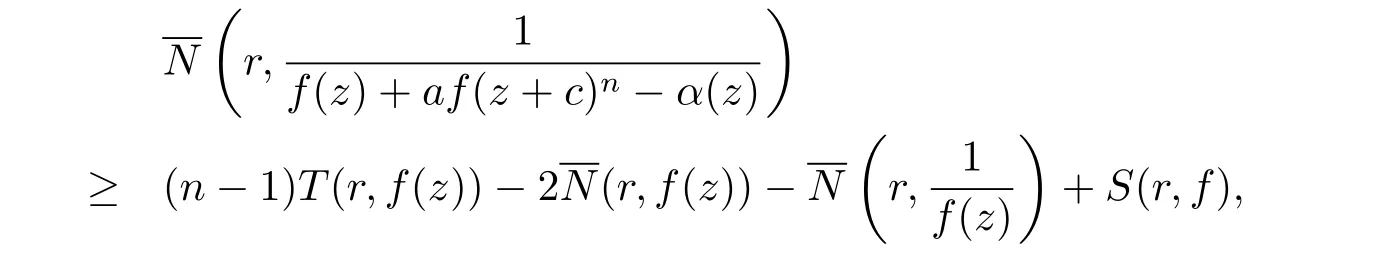
推論1.4設f(z) 為超越亞純函數, σ2(f)<1, c 為非零復常數, n 為正整數,為f(z) 的小函數, 則n ≥5 時, f(z)+af(z+c)n?α(z) 有無窮多個零點.

2 引理

引理2.1[7]設f(z) 為非常數亞純函數, σ2(f)<1, c 為非零復常數, 對任意的ε>0, 有

其中r →∞, r /∈E, E 為一個有限測度集.

由文獻[7, 引理8.3], [14, p. 66] 及[15, 引理1], 得到下面的引理2.2.

引理2.2設f(z) 為非常數亞純函數, σ2(f)<1, c 為非零復常數, 則

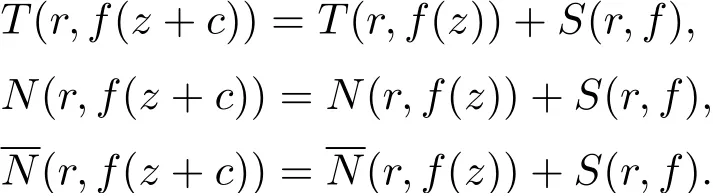
引理2.3[16]設f(z) 為有限級亞純函數, 滿足N(r,f) = S(r,f), H(z,f) 是形如(1.1)式的差分多項式, 且H(z,f) 中僅有一個單項式具有最高次數dH, 則

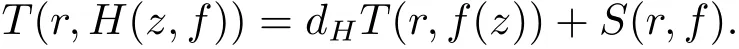
由文獻[16, 定理1] 和[17, 引理2], 得到下面的引理.

引理2.4設f(z) 為超越亞純函數, σ2(f)<1, H(z,f) 是形如(1.1) 式的差分多項式, 則

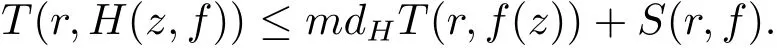
3 定理1.1–1.4 的證明

定理1.1的證明 記

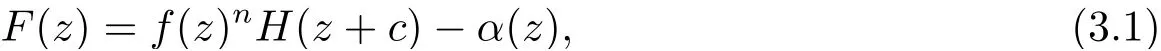
則

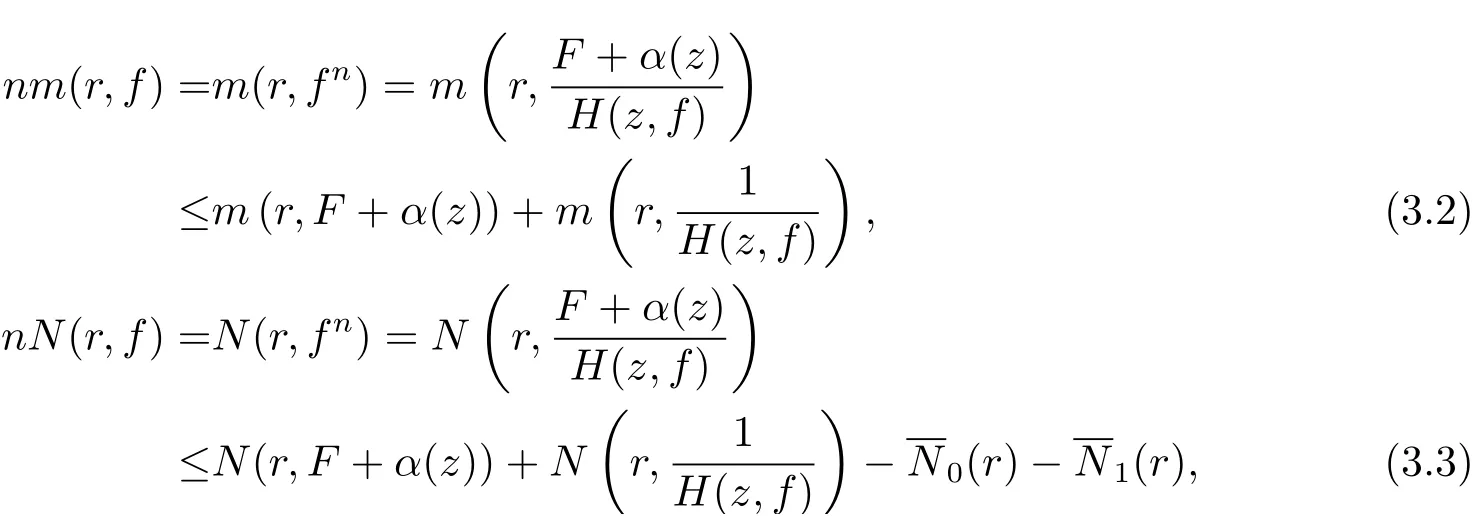
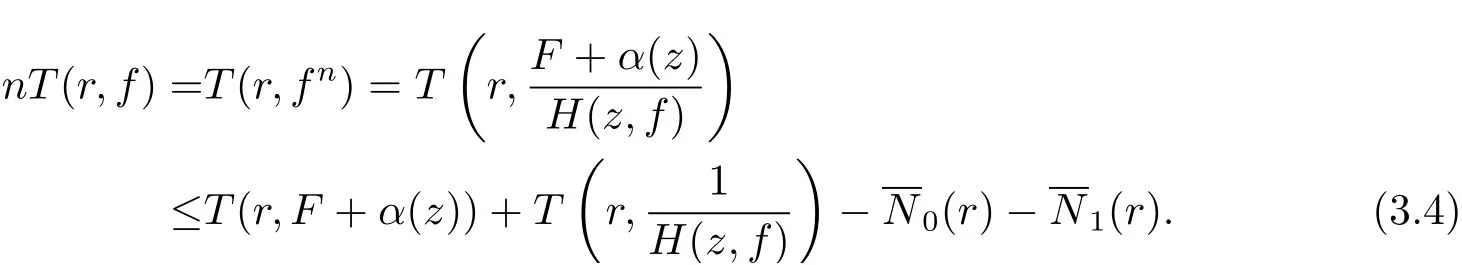
由(3.1) 式可知F +α(z)=fnH(z,f), 則有

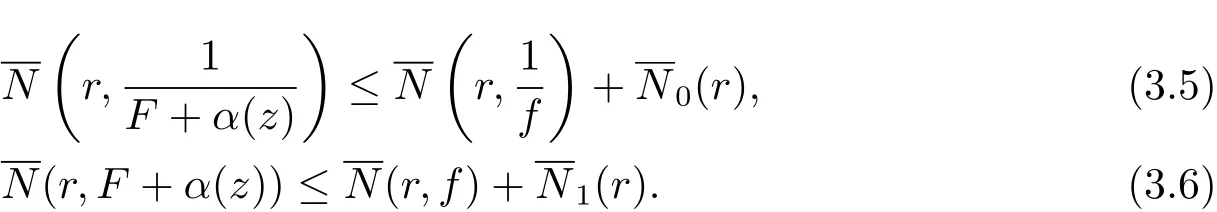
再由關于三個小函數的第二基本定理及(3.5)–(3.6) 式, 可知

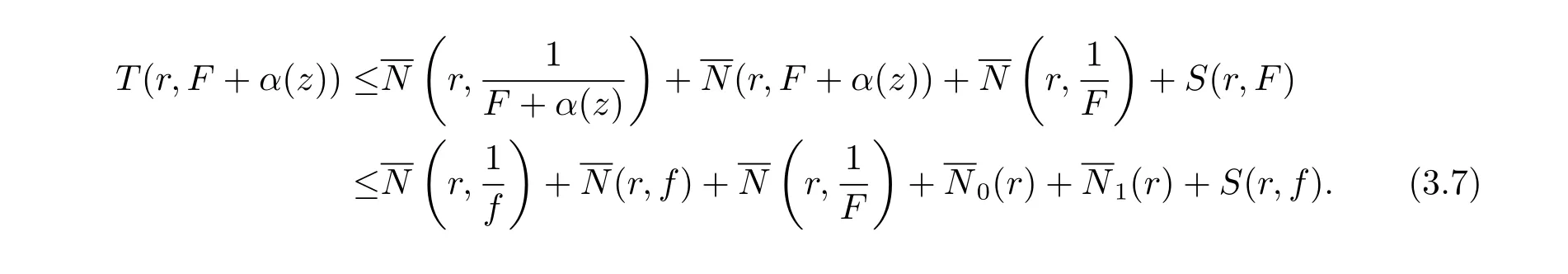
又由引理2.4 可知

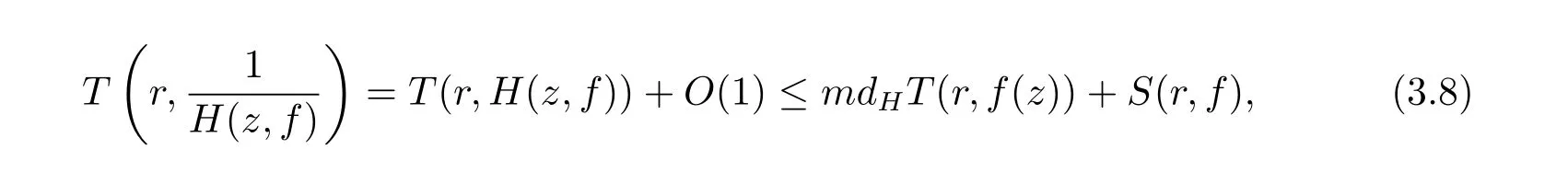
從而將(3.7)–(3.8) 式代入(3.4) 式可得

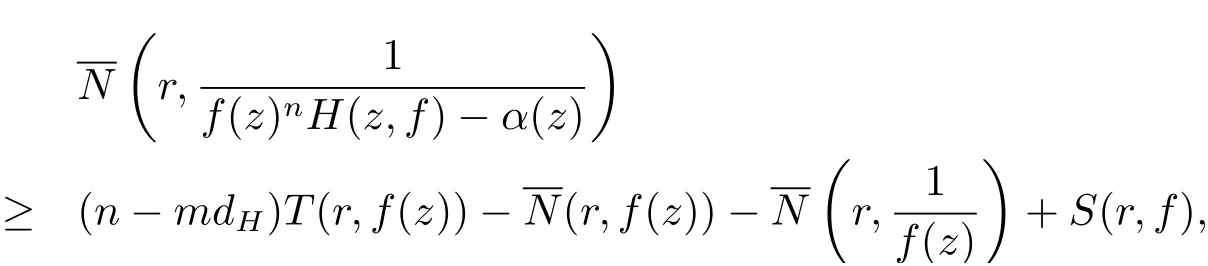
其中r →∞, r /∈E, E 為一個有限測度集.

定理1.2 的證明記則

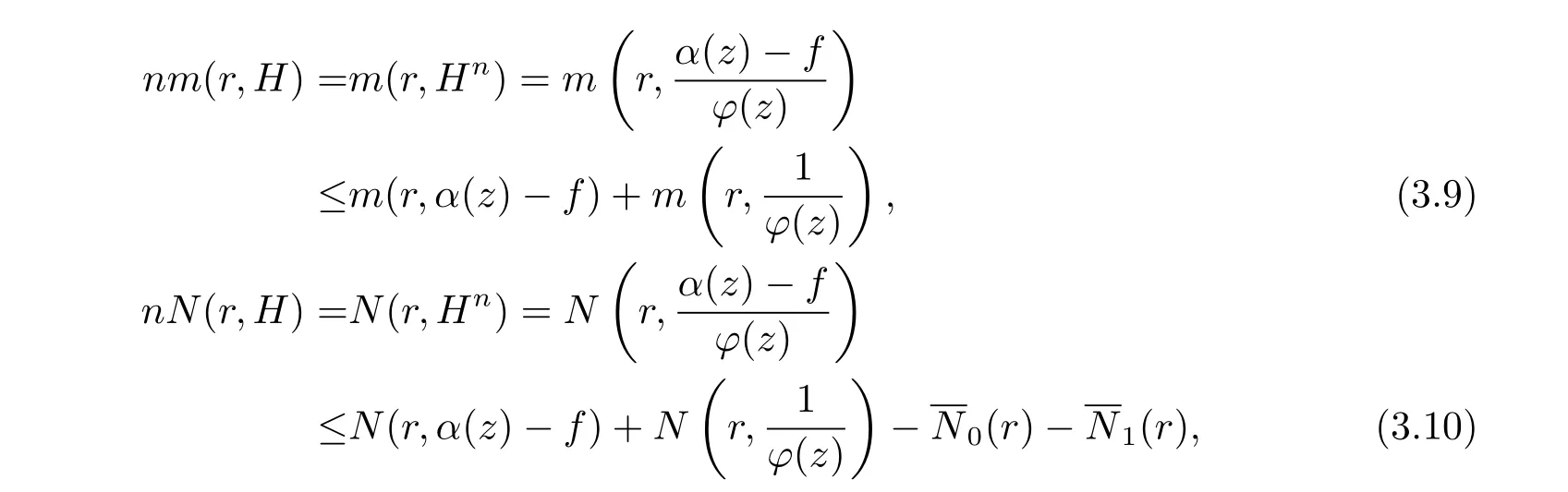
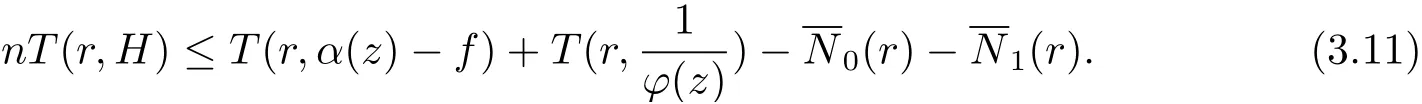
由N(r,f)=S(r,f), 可知N(r,H)=S(r,f). 所以

再由關于三個小函數的第二基本定理及(3.12)–(3.14) 式可知

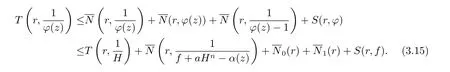
又由引理2.3 可知

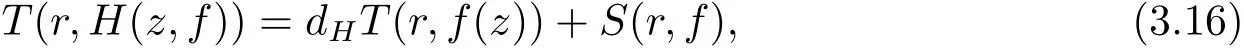
從而將(3.15)–(3.16) 式代入(3.11) 式可得

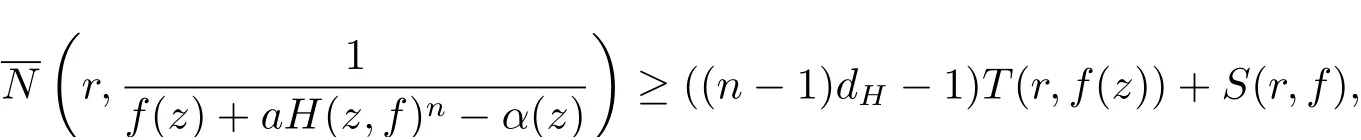
定理1.3 的證明記則

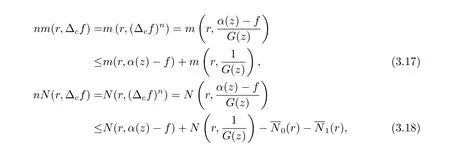
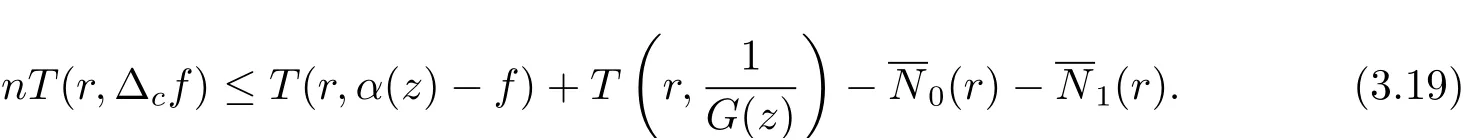
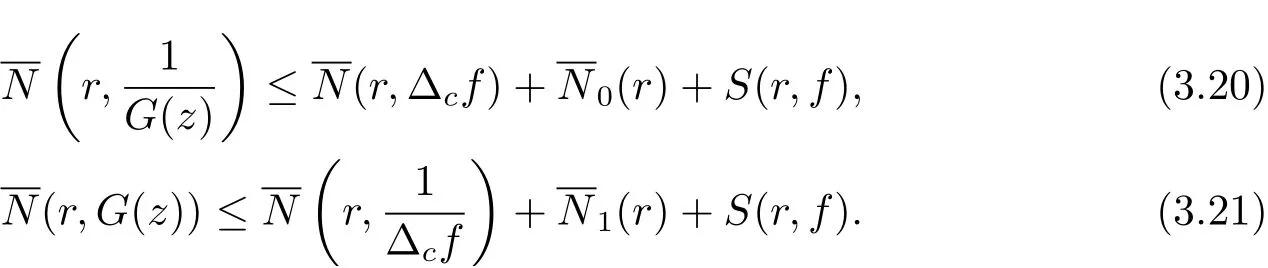
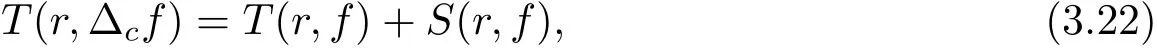
再由關于三個小函數的第二基本定理及(3.20)–(3.22) 式可知

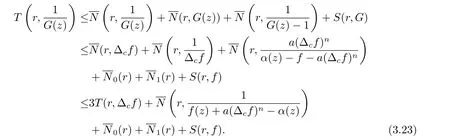
從而將(3.22)–(3.23) 式代入(3.19) 式, 可得

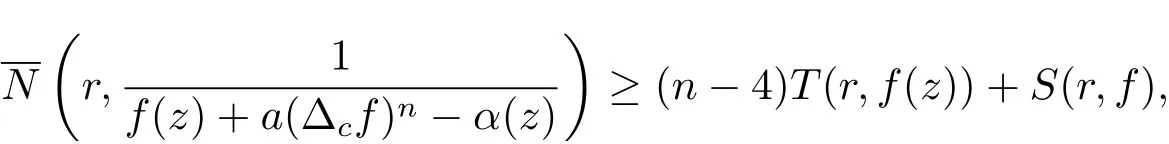
其中r →∞, r /∈E, E 為一個有限測度集.

所以n ≥5 時, f(z)+a(f(z+c)?f(z))n?α(z) 有無窮多個零點.

定理1.4 的證明記則

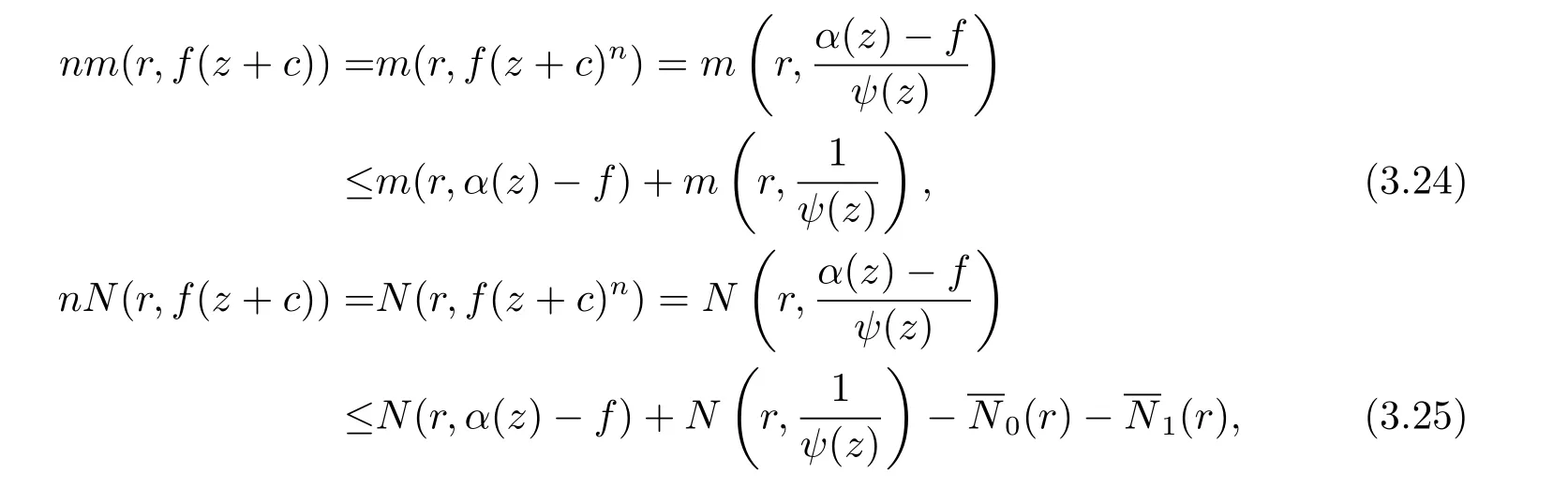
由(3.24)–(3.25) 式, 可得

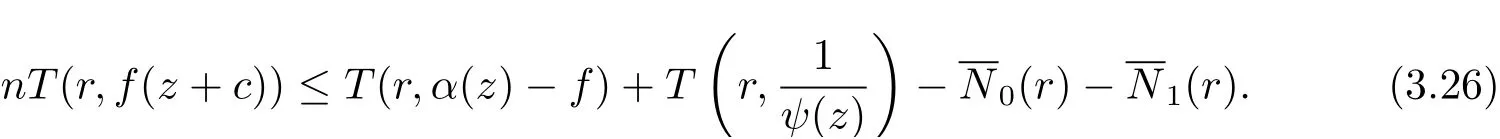
由引理2.2, 可知

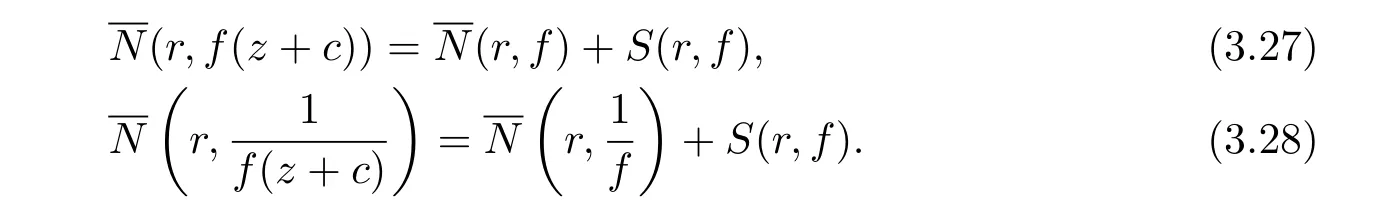
所以

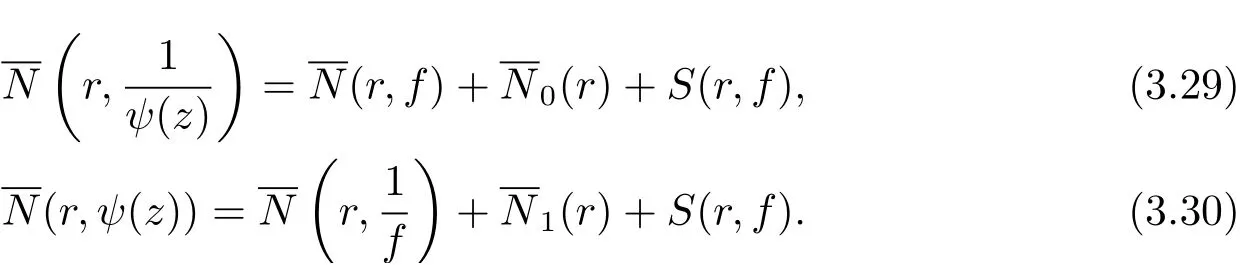
再由關于三個小函數的第二基本定理及(3.29)–(3.30) 式, 可知

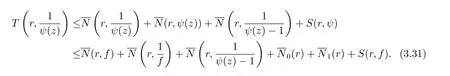
又由引理2.2 可知

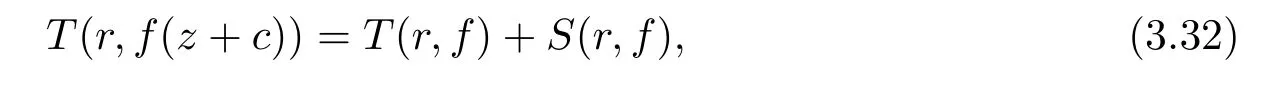
從而將(3.31)–(3.32) 式代入(3.26) 式可得

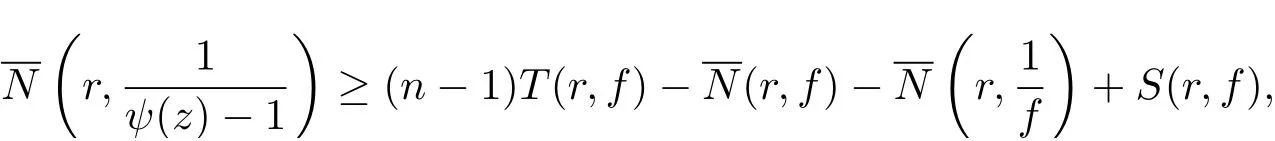
即