四元數(shù)Sylvester 方程的Toeplitz 約束解及其最佳逼近

黃敬頻,藍(lán)家新,毛利影,王 敏

(廣西民族大學(xué)理學(xué)院, 廣西南寧530006)

1 引言

Sylvester 方程是矩陣?yán)碚撗芯恐蟹浅Ｖ匾囊活惥仃嚪匠? 它在特征結(jié)構(gòu)配置、航天控制技術(shù)、微分方程數(shù)值解、模式識別等領(lǐng)域都有實(shí)際應(yīng)用[1?3]. 目前, 關(guān)于Sylvester 方程的解與約束解人們多在實(shí)數(shù)域或復(fù)數(shù)域上討論, 并已取得豐富的成果[4?8], 而在四元數(shù)體上討論該方程的約束解問題甚少. 隨著四元數(shù)矩陣在圖像處理、飛行器姿態(tài)控制等方面的應(yīng)用發(fā)展[9,10], 討論四元數(shù)Sylvester 方程的約束解具有較大實(shí)際意義. Toeplitz 矩陣是一類特殊結(jié)構(gòu)矩陣, 它在信號壓縮感知、超視距雷達(dá)電離層相位擾動校正等方面有重要作用[11?13].

本文目的是把實(shí)數(shù)域上的Sylvester 矩陣方程AX ?XB = C 推廣到四元數(shù)體上討論,給出該方程存在Toeplitz 約束解的條件及解法, 同時討論它的最佳逼近問題.

幾年前，在外創(chuàng)業(yè)成功的柳中輝回村，村企聯(lián)合進(jìn)行新農(nóng)村建設(shè)，打造總占地14000余畝的潯龍河生態(tài)藝術(shù)小鎮(zhèn)。目前已投入140億元打造文化產(chǎn)業(yè)、教育產(chǎn)業(yè)、康養(yǎng)產(chǎn)業(yè)、生態(tài)產(chǎn)業(yè)、旅游產(chǎn)業(yè)。

用Rn×n,Cn×n,Qn×n分別表示全體n 階實(shí)矩陣、復(fù)矩陣及四元數(shù)矩陣集合;分別表示四元數(shù)矩陣A 的轉(zhuǎn)置、共軛、共軛轉(zhuǎn)置; A+表示A 的Moore-Penrose 廣義逆;表示四元數(shù)矩陣A 的Frobenius 范數(shù); vec(A) 表示矩陣A 按列順序拉直向量; A ?B 表示矩陣A 與B 的Kronecker 積. 下面給出相關(guān)定義和引理.

定義1.1設(shè)T =(aij)n×n∈Qn×n, 如果滿足aij=aj?i, 即

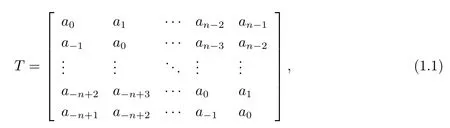
則稱形如(1.1)式的矩陣為四元數(shù)Toeplitz 矩陣,全體n 階四元數(shù)Toeplitz 矩陣記作TQn×n.

由于Xi∈Rn×n(i=0,1,2,3) 均是實(shí)Toeplitz 矩陣, 因此由引理1.1 可得

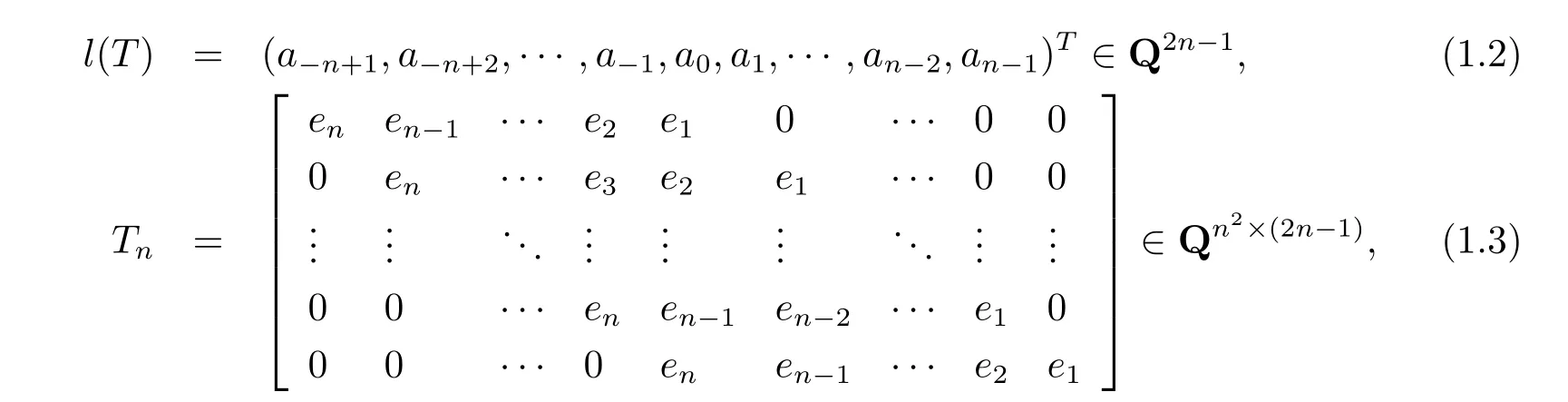
其中ei為單位矩陣In的第i 列. 易知Tn∈Rn2×(2n?1)是列正交的. 于是有

引理1.1設(shè)T =(aij)n×n∈Qn×n, 則

等價于

近日，楊女士因?yàn)檫B續(xù)幾天便血，到醫(yī)院做了肛腸檢查，結(jié)果竟檢查出腸道內(nèi)有幾顆大小不一的息肉，大的有豌豆大小。醫(yī)生要求楊女士進(jìn)一步進(jìn)行腸鏡檢查，但是楊女士對再次做腸鏡檢查和內(nèi)鏡手術(shù)十分排斥，希望能夠保守治療。

設(shè)X ∈TQn×n, 它在實(shí)數(shù)域R 上的分解式為X = X0+ X1i + X2j + X3k, 其中Xi∈Rn×n(i=0,1,2,3) 均是實(shí)Toeplitz 矩陣. 又設(shè)A,B,C ∈Qn×n在實(shí)數(shù)域R 上的分解式為A=A0+A1i+A2j+A3k,B =B0+B1i+B2j+B3k,C =C0+C1i+C2j+C3k, 其中Ai,Bi,Ci∈Rn×n(i=0,1,2,3), 則四元數(shù)體上Sylvester 方程

本文主要討論如下3 個問題.

據(jù)勘查，昌樂境內(nèi)藍(lán)寶石富礦區(qū)450平方公里，儲量數(shù)十億克拉，占全國藍(lán)寶石總儲量的90%以上，是繼泰國、澳大利亞、斯里蘭卡藍(lán)寶石礦之后世界上發(fā)現(xiàn)的第四大藍(lán)寶石礦床。昌樂藍(lán)寶石化學(xué)成分和礦物成分與緬甸、泰國、柬埔寨、斯里蘭卡等國家生產(chǎn)的藍(lán)寶石并無大的不同，“其化學(xué)成分主要是三氧化二鋁，就是金屬鋁的氧化物，因?yàn)楹形⒘吭剽伜丸F而呈現(xiàn)藍(lán)色，并且具有顆粒大、顏色純、質(zhì)量好、雙色性、易開采、奇異寶石多等特點(diǎn)。尤其是昌樂藍(lán)寶石獨(dú)有的雙色性，即表面呈現(xiàn)藍(lán)色，側(cè)面則是神奇的綠色，頗受國內(nèi)外珠寶界青睞，昌樂也因此被譽(yù)為“藍(lán)寶石之都”。

問題I給定四元數(shù)矩陣A,B,C ∈Qn×n, 求矩陣X ∈TQn×n, 使得AX ?XB =C.

問題II對給定的A,B,C ∈Qn×n, 求矩陣X ∈TQn×n, 使得||AX ?XB ?C||=min.

1.列舉法。在教學(xué)中，以形符為綱，選取造字能力強(qiáng)的常用形符，以形符為中心展開教學(xué)。例如形符“木”，后面列舉出“樸”、“機(jī)”、“杠”、“杖”、“村”、“材”、“枝”等由“木”這個形符構(gòu)成的形聲字。

問題III設(shè)問題I 的解集M ∈TQn×n是已知Toeplitz 矩陣, 求X 使得

2 問題I–II 的解

引理1.2[14]復(fù)數(shù)域上矩陣方程AX =C 有解的充要條件是AA+C =C. 此方程的通解和最小二乘解集均可表示為X = A+C +(I ?A+A)Y, 其中Y ∈Cn×n是任意矩陣, 且存在唯一極小范數(shù)最小二乘解X0=A+C.

其中l(wèi)(T),Tn分別如(1.2), (1.3) 式所示.

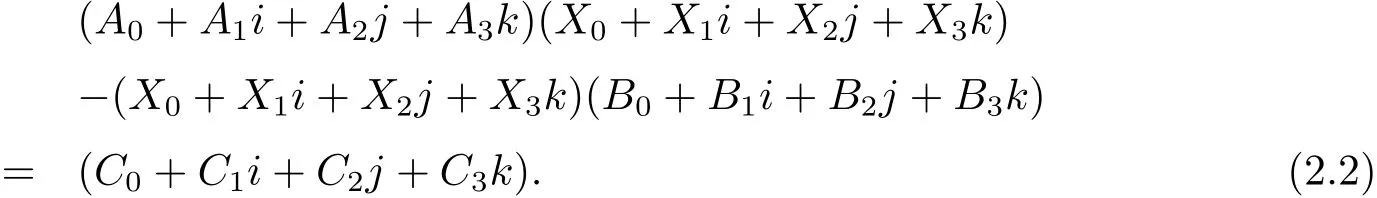
將(2.2) 式左邊展開, 并根據(jù)四元數(shù)矩陣實(shí)分解的唯一性, 可得

信息化的發(fā)展和運(yùn)用逐漸趨向成熟，各種信息化市場也逐漸趨向飽和。所以電信運(yùn)營商信息化業(yè)務(wù)的競爭十分激烈。不斷升級電信運(yùn)營商內(nèi)部的中心系統(tǒng)，采用先進(jìn)硬盤零件，引進(jìn)高科技技術(shù)。數(shù)據(jù)管理和監(jiān)控要求企業(yè)采取統(tǒng)一化的管理方法，因?yàn)槟Ｊ缴壓拖到y(tǒng)升級是依賴于這兩個因素的。信息化企業(yè)客戶數(shù)量龐大，流失起來也很快。信息化企業(yè)可以利用這個特點(diǎn)進(jìn)行客戶的快速挑選，確認(rèn)優(yōu)質(zhì)客戶并且把客戶流穩(wěn)定下來，發(fā)掘更多的潛在客戶渠道。信息化的企業(yè)還應(yīng)該注意企業(yè)本身的業(yè)務(wù)水平，有意識提高自己的業(yè)務(wù)能力，增強(qiáng)自己企業(yè)的市場競爭力。

(2)圓上的任意一點(diǎn)到定點(diǎn)(圓心)的距離等于常數(shù)(半徑)，而點(diǎn)M在橢圓上運(yùn)動時，點(diǎn)F1、F2的位置不發(fā)生變化.請同學(xué)們用文字語言歸納,橢圓上任意一點(diǎn)應(yīng)具有怎樣的性質(zhì)呢？

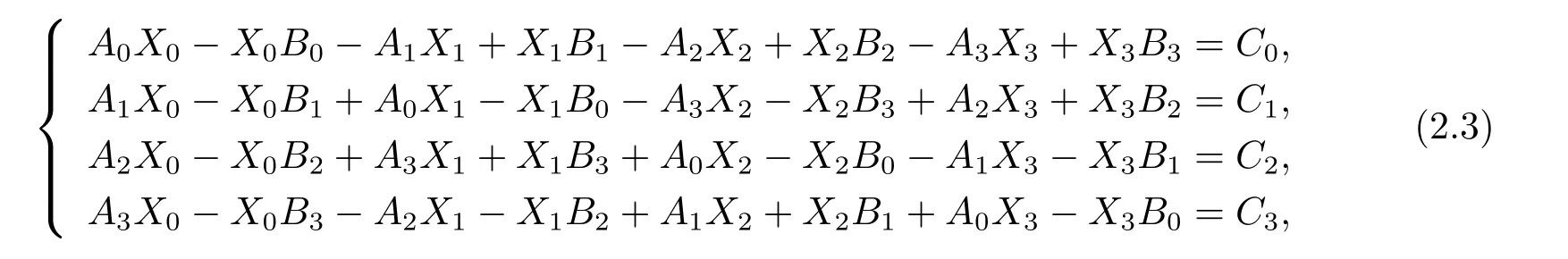
顯然, 一個四元數(shù)Toeplitz 矩陣(1.1) 由它的第n 行和第n 列共2n ?1 個元素唯一確定. 記

2.培養(yǎng)兒童思維和非智力因素的結(jié)合，有效彌補(bǔ)課堂過分強(qiáng)調(diào)智力訓(xùn)練的缺失。學(xué)習(xí)包含智力的訓(xùn)練和能力的培養(yǎng)，課堂文化的學(xué)習(xí)往往被認(rèn)為是智力的訓(xùn)練。在培養(yǎng)學(xué)生智力和能力的過程中，不能忽視非智力因素的培養(yǎng)。如情感、意志、氣質(zhì)、性格等。非智力因素的良好培養(yǎng)是智力和能力發(fā)展的驅(qū)動。情境教學(xué)強(qiáng)調(diào)培養(yǎng)興趣，著眼創(chuàng)造性，激發(fā)兒童情感，這正符合兒童非智力因素的培養(yǎng)要求。

其中Tn如(1.3) 式所示. 記

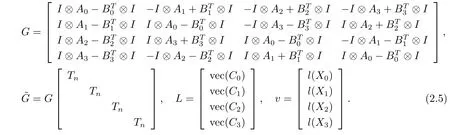
由于(2.4) 式等價于

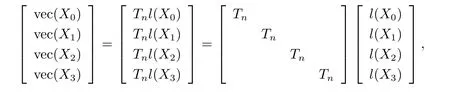
因此方程組(2.3) 等價于

第三,外源性與內(nèi)源性病原體所致盆腔炎,上述兩種病原菌也單獨(dú)存在,也可一并存在,病情較復(fù)雜一般需聯(lián)合用藥。

此外, 利用矩陣Frobenius 范數(shù)可得

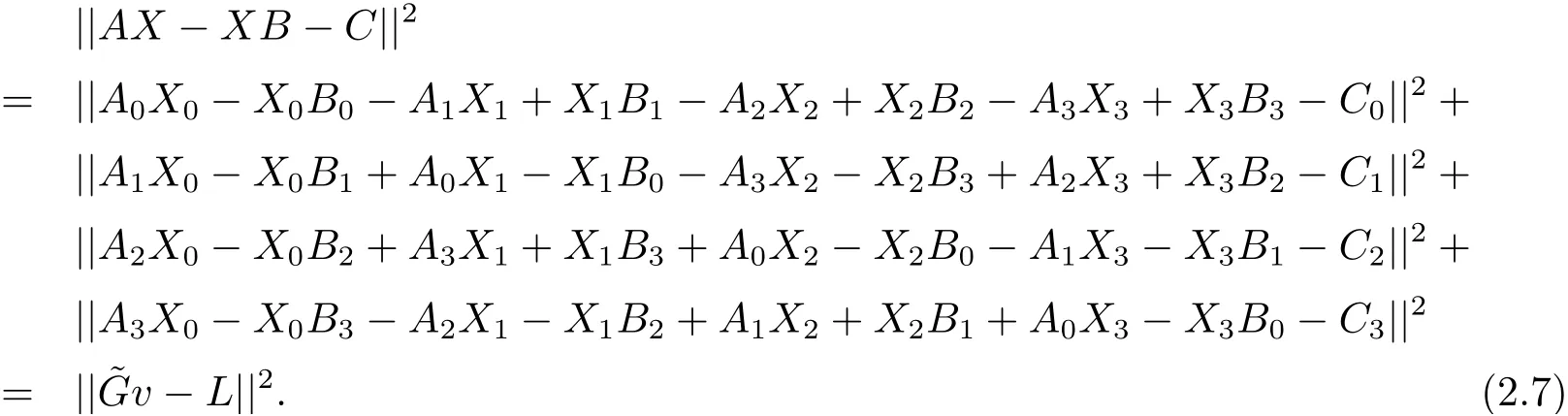
于是, 關(guān)于問題I–II 的解, 有如下的結(jié)果.

證當(dāng)X ∈SE時, 根據(jù)定理2.1 及(3.2) 式可知||X ?M||2= min其中是一個正對角矩陣. 當(dāng), 由引理1.2, 上式關(guān)于Y 的最小二乘解為(2.1) 存在唯一解因此不論哪種情況均有

低碳經(jīng)濟(jì)推動著會計(jì)理念改革，而會計(jì)理念改革也將加快全球低碳經(jīng)濟(jì)化的形成。為了緊跟低碳經(jīng)濟(jì)發(fā)展腳步，電力企業(yè)財務(wù)工作者必須改革傳統(tǒng)的會計(jì)管理理念以及操作技術(shù)。站在全面客觀的角度，綜合考慮企業(yè)低碳排放在市場需求與能源成本之間的關(guān)系，特別是在市場準(zhǔn)入、稅收政策、金融支持等方面的影響。

其中這里的符號意義與前面所示相同.

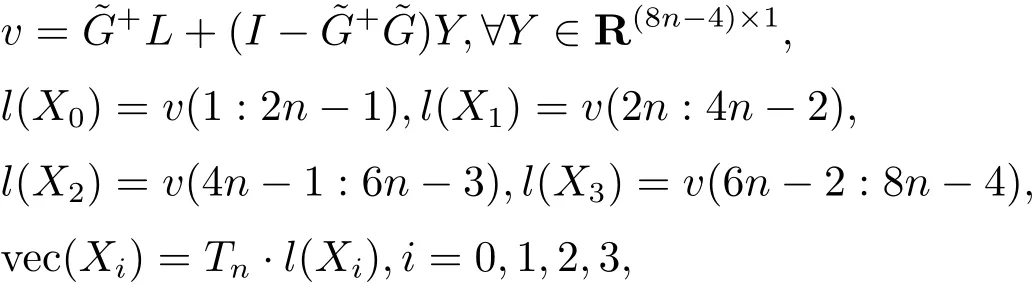
證由方程組(2.6) 及引理1.2 可得, 方程組(2.1) 存在四元數(shù)Toeplitz 解?方程組(2.6)有解=L. 有解時, (2.1) 的Toeplitz 解顯然由(2.8) 式給出. 無解時, 由(2.7) 式可得= min ?= min. 因此(2.1) 式的最小二乘Toeplitz 解仍為(2.8) 式. 證畢.

3 問題III 的解

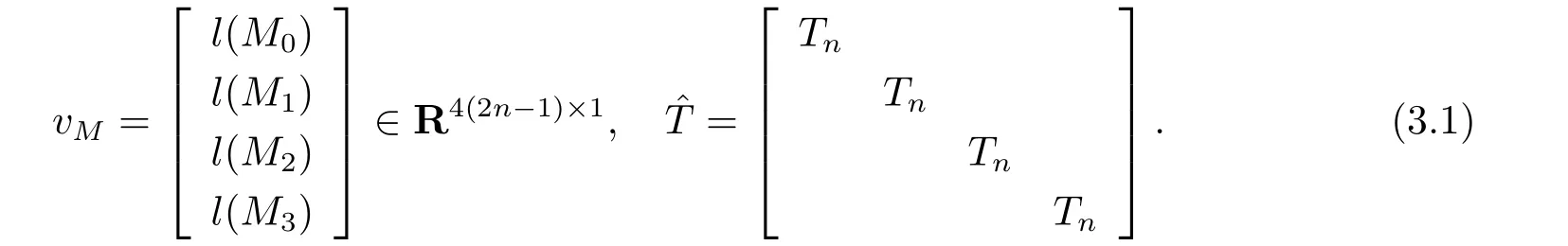
則有

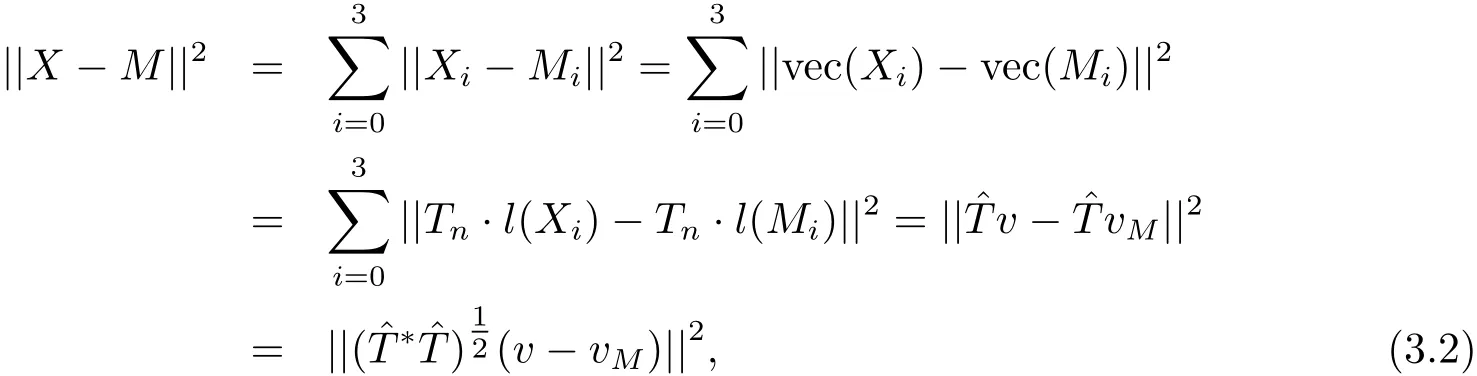
其中

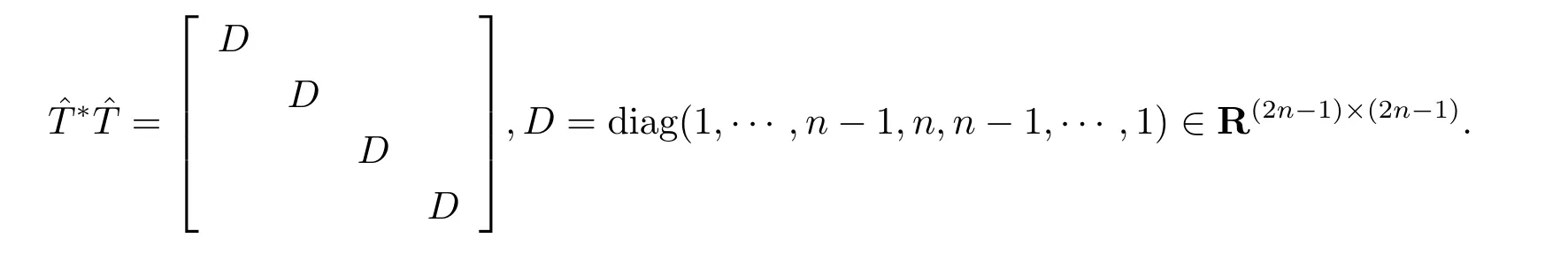
于是關(guān)于問題III, 有如下結(jié)果.

定理3.1設(shè)問題I 的解集是已知四元數(shù)Toeplitz 矩陣, 則在SE中使得=min 的解存在, 且有如下表達(dá)式

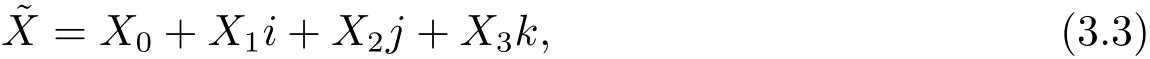
無解時, 它的最小二乘Toeplitz 解仍為(2.8) 式, 其中

80后女詩人，作品先后發(fā)表于《青年文學(xué)》《大鵬灣》《衡陽日報》《衡陽晚報》等報刊雜志。2006年至今堅(jiān)持在網(wǎng)上寫了數(shù)百首詩歌，并引起關(guān)注。詩歌《每天吃一點(diǎn)毒藥》曾獲2006-2007年網(wǎng)絡(luò)文學(xué)節(jié)詩歌三等獎。

定理2.1給定四元數(shù)矩陣A,B,C ∈Qn×n, 則Sylvester 方程(2.1) 存在四元數(shù)Toeplitz解的充要條件是?G ?G+L=L. 有解時, 它的一般Toeplitz 解為

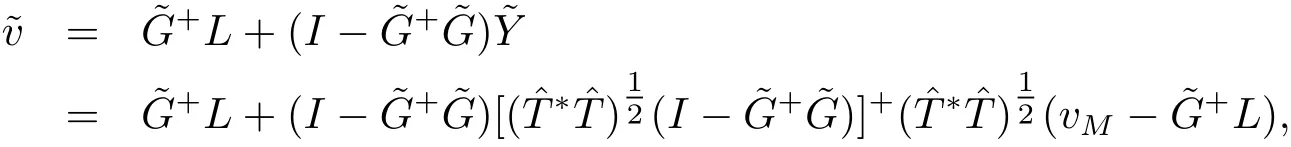
Nif、CsA因價格低廉、臨床療效好，已成為臨床上治療高血壓、心絞痛和器官移植術(shù)后常規(guī)服用藥物。有研究顯示，Nif、CsA均會引起牙齦增生，尤其當(dāng)兩種藥物聯(lián)合應(yīng)用時，牙齦增生也明顯加重[5]，影響患者的咀嚼功能和牙周組織的健康。目前，藥物性牙齦增生的具體發(fā)病機(jī)制尚不清楚，多認(rèn)為是成纖維細(xì)胞增殖活性增強(qiáng)和(或)凋亡受到抑制，進(jìn)而促進(jìn)成纖維細(xì)胞的活性[12],導(dǎo)致膠原纖維合成與分解代謝失衡，引起以膠原纖維為主的細(xì)胞外基質(zhì)(Extracellular matrix，ECM)的大量聚積[8]，從而導(dǎo)致了牙齦的纖維性增生。

根據(jù)定理2.1 和定理3.1, 我們給出問題I–III 的求解步驟:

步1寫出四元數(shù)矩陣A,B,C 的實(shí)分解式, 即A = A0+A1i+A2j +A3k,B = B0+B1i+B2j+B3k,C =C0+C1i+C2j+C3k.

步2按(2.5) 式寫出實(shí)矩陣?G 和實(shí)向量L.

步3檢驗(yàn)條件?G ?G+L=L 是否成立.

i) 若條件成立, 說明問題I 有解, 并按(2.8) 式寫出其Toeplitz 解集SE;

ii) 若條件不成立, 說明問題I 無解, 此時問題II 的最小二乘Toeplitz 解集仍為SE.

兩組的生活質(zhì)量、滿意度評分進(jìn)行比較,觀察組的生活質(zhì)量、滿意度評分高于對照組,統(tǒng)計(jì)學(xué)有意義(P<0.05);見表2。

步4在問題I 有解時, 對給定的四元數(shù)Toeplitz 矩陣M, 按(3.1) 式寫出對應(yīng)的實(shí)向量vM.

目前,海上風(fēng)電主要采用長距離海底交流電纜傳輸?shù)姆绞竭M(jìn)行傳輸。相比陸上的架空線路,海底交流電纜的容性充電功率較大,隨著離岸距離的增加,可能導(dǎo)致并網(wǎng)點(diǎn)以及所接入?yún)^(qū)域電網(wǎng)的節(jié)點(diǎn)出現(xiàn)過電壓,同時也會增加電網(wǎng)內(nèi)部的網(wǎng)絡(luò)損耗。因此,對于大規(guī)模海上風(fēng)電場所接入的區(qū)域電網(wǎng),研究其無功電壓優(yōu)化問題,以提高節(jié)點(diǎn)電壓質(zhì)量和減小網(wǎng)絡(luò)損耗,是海上風(fēng)電并網(wǎng)研究的重要課題之一[1-3]。

步5按(3.3) 式寫出問題III 的最佳逼近解?X, 即由vec(Xi) = Tn·l(Xi),i = 0,1,2,3,可得出4 個實(shí)Toeplitz 矩陣Xi,i=0,1,2,3, 從而獲得?X =X0+X1i+X2j+X3k.

4 數(shù)值算例

算例給定下列四元數(shù)矩陣

試討論Sylvester 方程(2.1) 的Toeplitz 解的存在性.

解四元數(shù)矩陣A,B,C 的實(shí)分解矩陣分別為

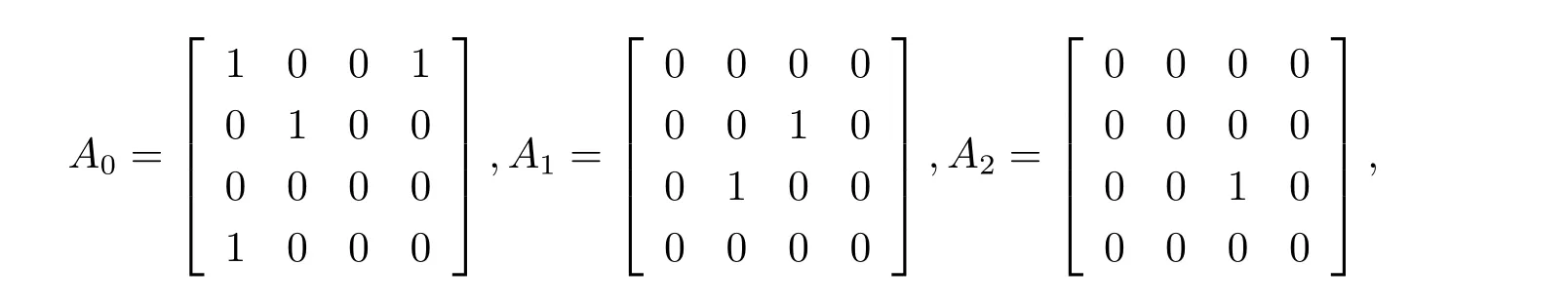
5 結(jié)語

本文提出一種判斷四元數(shù)Sylvester 方程是否具有Toeplitz 約束解的方法. 我們根據(jù)Toeplitz 矩陣的結(jié)構(gòu)特點(diǎn), 給出四元數(shù)Toeplitz 矩陣的新刻劃. 利用四元數(shù)矩陣的實(shí)分解和矩陣的Kronecker 積, 把約束方程問題轉(zhuǎn)化為無約束方程問題, 解決了四元數(shù)乘法非交換的限制, 得到了四元數(shù)Sylvester 方程具有Toeplitz 解的充要條件, 以及它的Toeplitz 解集和最小二乘解集SE. 此外, 利用矩陣Frobenius 范數(shù)性質(zhì), 在Toeplitz 解集的條件下, 獲得SE與預(yù)先給定的四元數(shù)Toeplitz 矩陣M 有極小Frobenius 范數(shù)的最佳逼近解. 本文結(jié)果可為解決相關(guān)約束四元數(shù)矩陣方程問題提供有益參考.