對疊加問題中一道定值模型解法探討

陳 明

(江西省玉山縣第一中學 334700)

一、引言

疊加問題是高中運動學中學常見類型，知識綜合性大，難度大，特別是物體間的相對運動，很多同學難以理解.本文將結合一道定值問題，對這類問題的求解方法進行探討.

二、例題解析

例長為L、質量為M的平板小車停在光滑水平面上，質量為m的木塊(可視為質點)以速度v0滑上小車的左端，最后停在小車的右端，如圖1甲所示；若小車以速度v0向左運動時，將木塊輕輕地放在小車左端，如圖1乙所示，則( ).

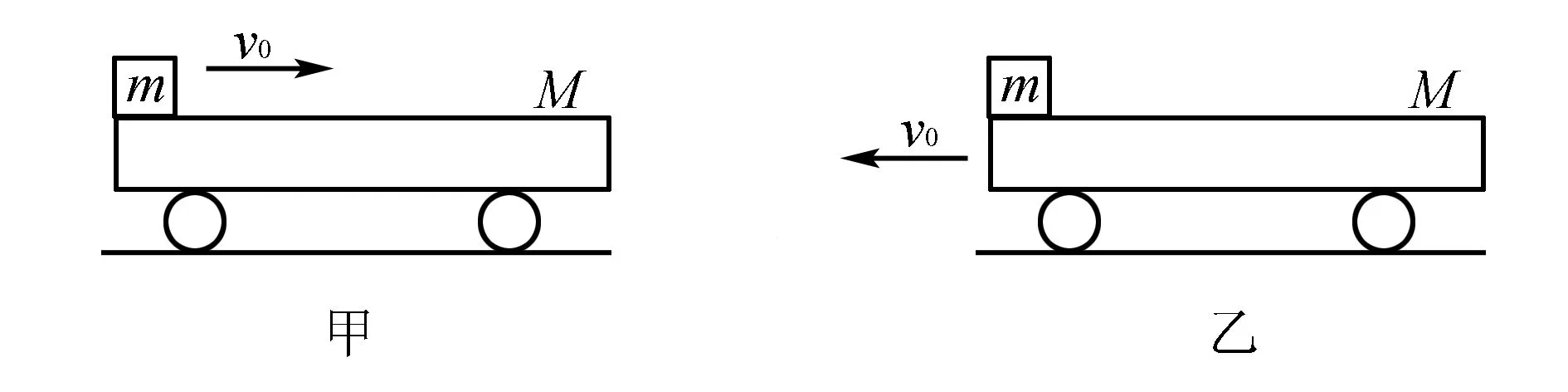
圖1

A.木塊最終剛好停在小車右端

B.木塊最終停在小車上，但還離右端一段距離

C.木塊將滑出小車

D.兩種情況中木塊相對小車滑行的時間相等

解法一根據運動學知識求解.

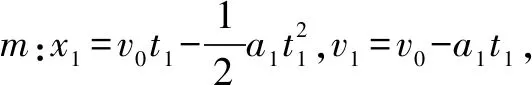
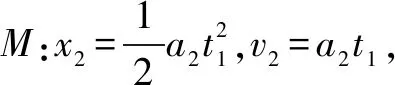
木塊最終停在小車右端，所以v2=v1

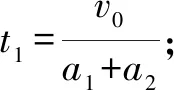
對乙，木塊和小車受力情況與甲相似，因此在運動過程中木塊和小車加速度的大小與圖甲對應的加速度大小相等.假設木塊最終停在小車上，則木塊與小車最終的速度大小相等，

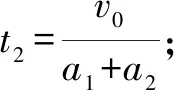
因此有t1=t2，△L=L，故假設成立，木塊恰好停在小車的右端.

解法二根據動量知識求解.

對甲，根據動量守恒定律有mv0=(M+m)v1，

根據能量守恒有

對乙，根據動量守恒定律有Mv0=(M+m)v2，

根據能量守恒有

因此有△x=L，t1=t2.

解法三轉換參考系.

對甲，木塊：a1=f/m，方向向左，

小車：a2=f/M，方向向右，

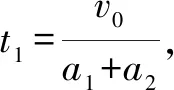
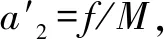
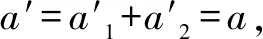
解法四利用v-t圖像求解.

根據木塊和小車運動關系，甲中木塊和小車的v-t圖像如圖2所示，乙中木塊和小車的v-t圖像如圖3所示，對于圖甲、圖乙，木塊和小車受力情況相似，因此甲中木塊和小車在運動過程中的加速度的大小與乙中對應的加速度大小相等，對應v-t圖像中的直線斜率大小相等，從而可得兩種情況下木塊相對小車滑行的時間相等.

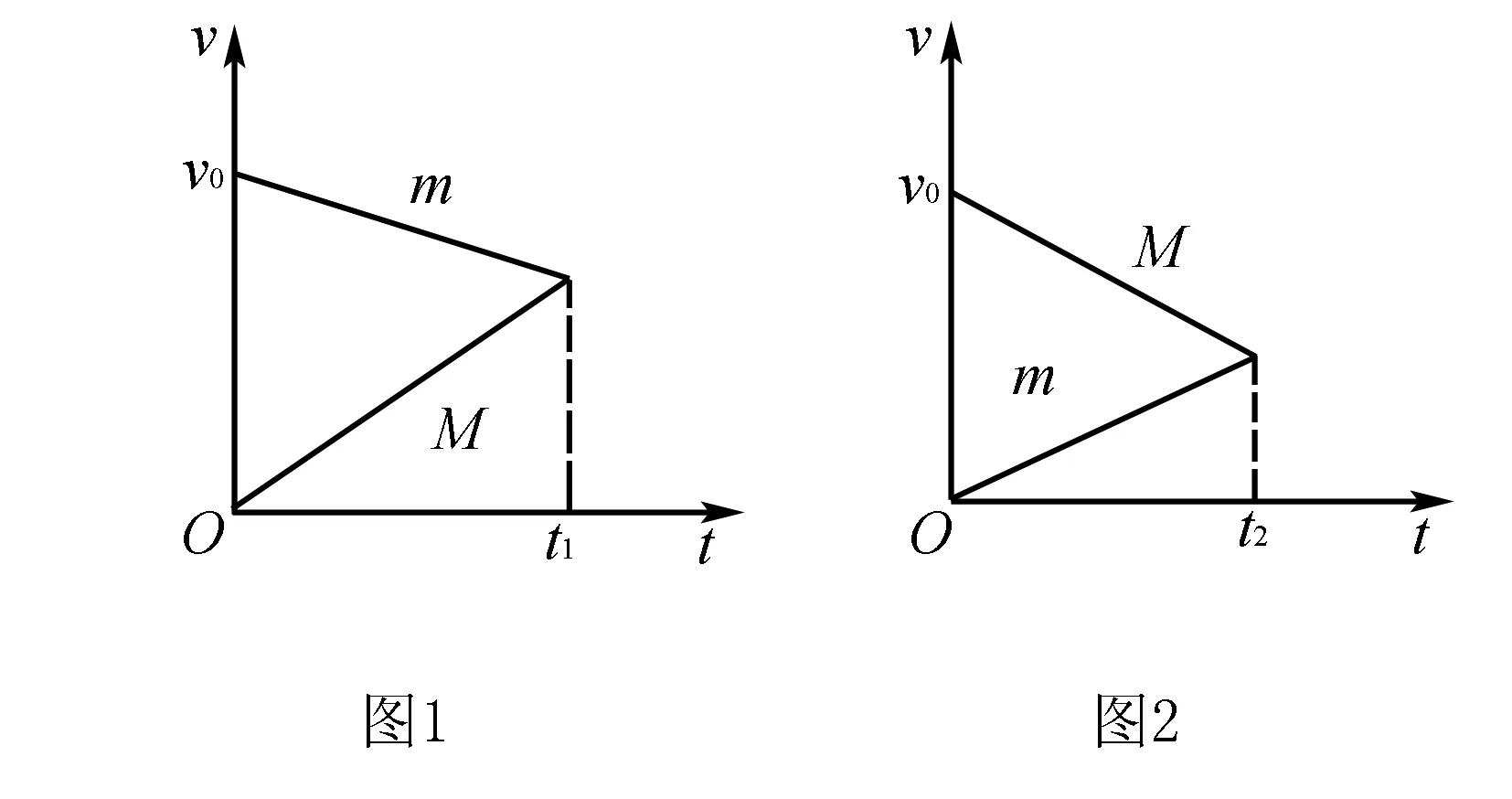
甲、乙v-t圖象中的兩直線所圍三角形為木塊與小車之間的相對距離，即木塊在小車上滑行的距離，因為兩v-t圖象中時間相等，所以兩v-t圖象中三角形所圍面積相等，即兩種情況下木塊在小車上滑行的距離相等.

因此兩種情況下木塊在小車上滑行的距離相等，木塊在小車上滑行的時間相等.

通過以上幾個方法分析，不難得出：

1.兩種情況下木塊在小車上滑行的距離相等，木塊在小車上滑行的時間相等.這種模型是定值模型.

2.在解題過程中，可以從不同角度來分析問題，拓寬思路提升能力.

3.在這幾種求解方法中，都設定了未知量，利用未知量但并沒有求解未知量，這是一種較好的解題思路：“設而不求”，巧設未知量以求解問題.