基于可拓理論的山區鐵路樞紐土質高陡邊坡穩定性評價

邱鈺峻 但鵬飛 郭 斌

(1.西南交通大學土木工程學院 四川成都 610032；2.中鐵十八局集團有限公司 天津 300222)

1 引言

我國地形西高東低，山區面積占國土面積的三分之二，西部山區鐵路路網嚴重不足。自“十三五”以來，為了緩解不均衡的區域布局，我國鐵道部門正不斷擴大西部山區鐵路網規模并完善我國路網規模[1]。在此過程之中，將不可避免地修建大量山區鐵路樞紐，如重慶西站、貴陽北站、溆浦南站等。

西南山區地形起伏大，地質構造復雜，地殼活動強烈，土質高陡邊坡極為常見。土質高陡邊坡坡體具有脆弱性與不穩定性，在樞紐修筑與運營過程之中，常常由于人為活動的原因，產生崩塌、滑坡等地質災害，危及施工與運營安全。鐵路樞紐作為鐵路線網建設的重要節點，在協調不同線路的順暢銜接利用、實現大量客流及貨流和車流的集散與中轉等方面都起著至關重要的作用，一旦受到地質災害的影響，除了樞紐自身的破壞以外，還會阻斷關聯線路的正常運營，甚至導致區域交通崩潰，造成巨大的經濟損失。由此可見，研究如何對鐵路樞紐高陡土質邊坡進行穩定性評價以指導高陡邊坡防護，具有極大的實際意義。

土質高陡邊坡是一個受多種因素影響、不確定性大且極為脆弱的動態系統[2-3]。出于土體的復雜性和不確定性，許多因素無法準確獲得，只能定性表示，這種定性與定量信息共存的情況必然會對土質高陡邊坡穩定性評價結果的合理性產生不利影響。近年來，國內外學者開始引入一些新的理論與方法應對定性與定量信息共存的情況，并取得了一定成果，如粗糙集理論[4]、可拓理論[5]、神經網絡[6]等。其中，可拓理論具有能高效處理定性、定量信息并存問題的優點[7]，已在決策支持、故障檢測、災害評估等領域得到了應用。因此，本文引入可拓理論展開對鐵路樞紐土質高陡邊坡穩定性評價的研究。

2 模型構建

2.1 邊坡穩定評價指標體系

穩定評價指標作為反映影響邊坡穩定性的主要因素，其選擇和確定是整個評價體系的基礎。本文通過分析大量山區鐵路土質高陡邊坡技術經濟資料，結合專家意見，選擇地形地貌V1、地質條件V2、氣候水文V3和地震V4四個一級指標，一級指標包含數個二級指標，如圖1所示。

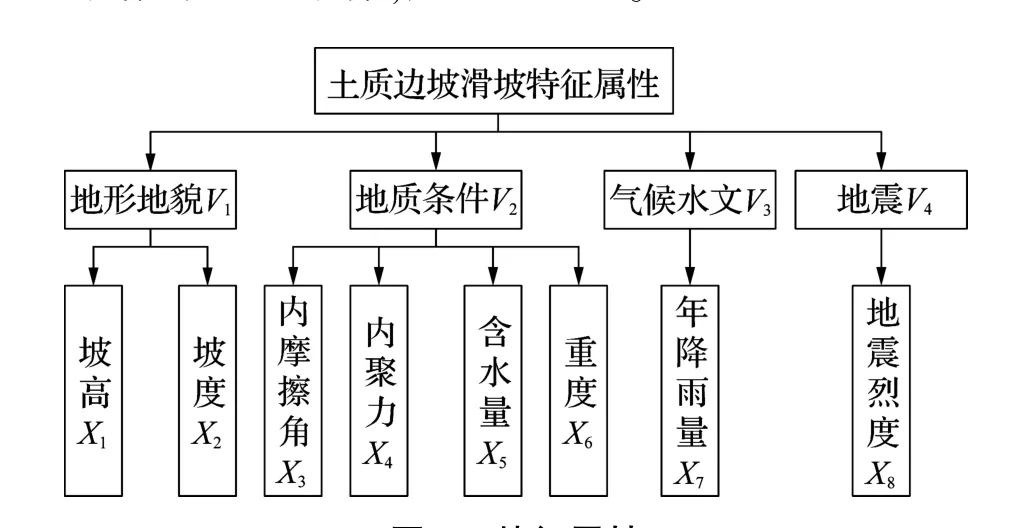
圖1 特征屬性

2.2 指標權值的確定

2.2.1 基于OWA算子的賦權方法基本原理

邊坡穩定影響指標的權值反映了不同因素對邊坡穩定性的影響程度，因此確定不同指標的權重是進行邊坡穩定性評價的第一步。

目前常用的賦權方法(德爾菲法、層次分析法等)大多依據專家的主觀判斷對不同指標的重要程度進行打分，其過程中不可避免地由于專家的主觀偏好產生極值。若不對極值進行處理，勢必會影響權重的公正性。針對該問題，本文基于OWA(Ordered weighted averaging)算子來計算土質高陡邊坡穩定影響指標權重。OWA算子是一種群集結方法，可用于定量表示因素間相互影響，將其引入與權重計算可降低由專家主觀原因產生的極值對結果的影響，可使結果更合理、客觀[8]。

利用OWA算子計算權重的步驟如下:

(1)專家打分

由n名專家對邊坡穩定影響指標Xi的重要性進行打分，可得各指標分值(x1，x2，…，xn)。將所得分值按小到大排列，并從1開始進行編號，得到分值組 y1≤y2≤…≤yk≤…≤yn。

(2)位置賦權

根據排列組合數對各評價指標Xi分值組(y1，y2，…，yn)賦權，得到權向量 αk:

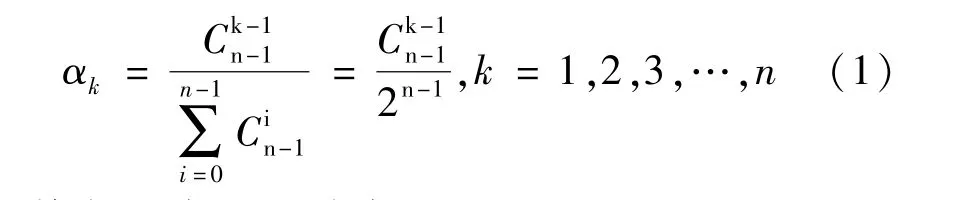
其中，根據二項式定理:

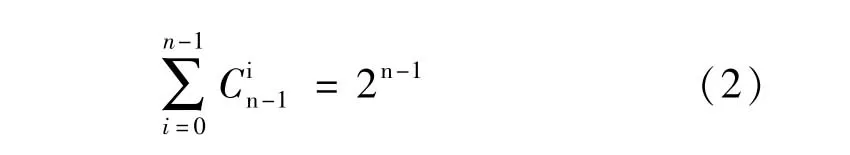
(3)確定絕對權重

利用權向量 αk對分值組(y1，y2，…，yn)加權，得到邊坡穩定影響指標Xi的絕對權值w′i:

(4)確定相對權值

根據指標Xi絕對權值w′i其相對權值wi:

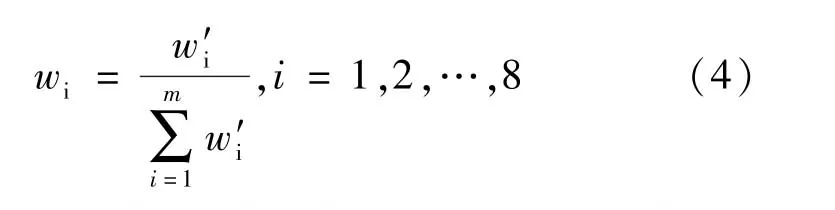
根據以上步驟，可得各邊坡穩定影響指標權重。

2.2.2 權值計算

本文的研究共咨詢了五位專家對邊坡穩定性影響因素重要程度進行打分。為了保證打分結果的規范與統一，令分值取值范圍為0～10，且是0.5的整倍數，分值越高則說明該專家認為該指標越重要，打分結果見表1。

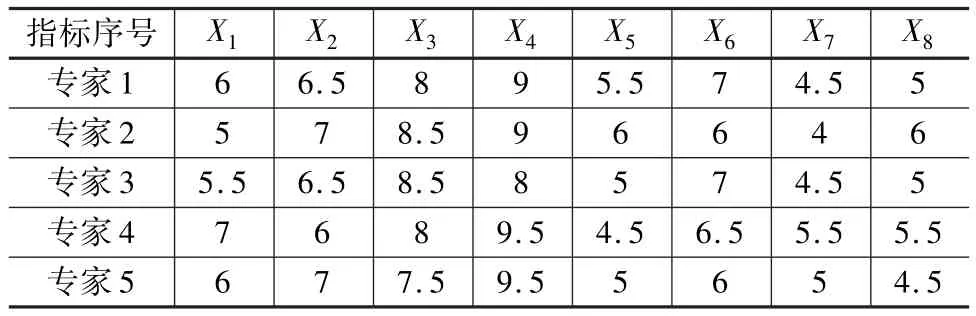
表1 各特征屬性得分結果

由公式(1)和(2)，計算得各評價指標絕對權值:w′1＝5.875、w′2＝ 6.625、w′3＝ 8.125，w′4＝ 9.094、w′5＝5.156、w′6＝ 6.500、w′7＝ 4.656、w′8＝ 5.156。 根據式(3)求得各指標權值見表2，其中一級指標權值為二級指標權值之和。

2.3 標準化處理

本文通過理論分析并結合前人研究成果[9-11]，將不同工況下的土質高陡邊坡穩定程度分為穩定、較穩定、基本穩定、較不穩定、不穩定五個等級。若指標實際值大于表中最大范圍時，按值域范圍最大值選取。各工況條件如表3所示。為了避免不同指標量綱對評價的影響，應把各指標數值進行標準化處理。對于指標值越大對邊坡穩定性越有利的指標，標準化公式為:

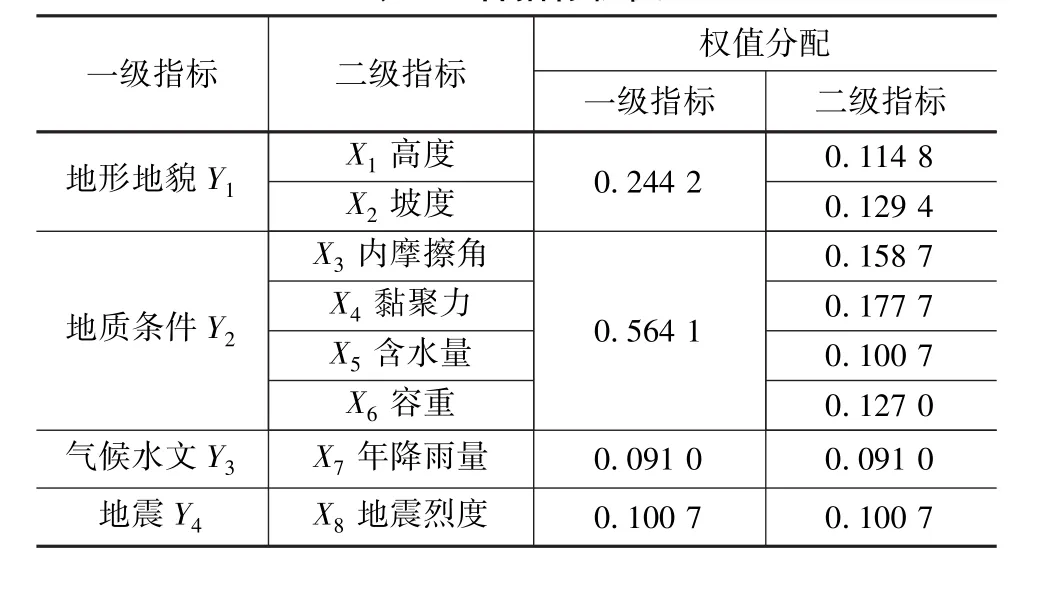
表2 各指標權值

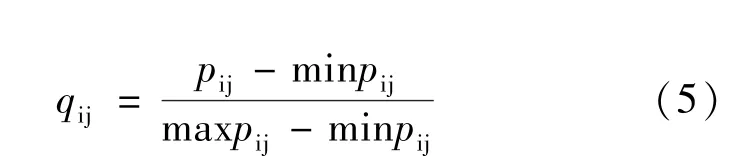
對于指標越大對邊坡穩定性越不利的指標，標準化公式為:

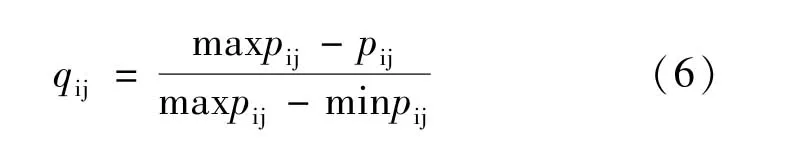
式中，qij為標準化處理后的指標值；pij為指標原始值；maxpij和minpij分別為其最大和最小值。

根據式(5)和式(6)，對表3中的等級量值范圍進行標準化處理，得到表4。

表3 _指標等級量值

表4 _評價指標的等級量值范圍(無量綱)

2.4 可拓評價

可拓理論是最早由蔡文提出的新方法，用以解決各種矛盾問題。將物元作為其基本邏輯，以個體名稱N、特征C以及特征值V作為基本因素，并用R＝{N，C，V}描述事物個體[12]。為了減少信息不確定性對土質邊坡評價結果的干擾，確保評價準確性，本文采用依次進行二級指標和一級指標的可拓評價的兩層可拓評價，得到邊坡穩定性評價結果。

2.4.1 二級指標的可拓評價

(1)經典域、節域:依照本文上述評價標準，本文將土質高陡邊坡穩定性分為d個等級(d＝1，2，…，e)，其經典域和節域可表示為

式中，R0d為經典域；N0d為穩定性等級；Cl為各土質邊坡穩定性評價指標；V0dl＝＜a0dl，b0dl＞為對應等級的評價指標量值范圍；Rk為節域；Nk為邊坡個體；Vkl＝＜akl，bkl＞為評價指標等級量值范圍的最小值到最大值，即 ＜ a0dl，b0dl＞ ? ＜ akl，bkl＞ (l＝1，2，…，n)。

(2)待評價土質邊坡:根據表4得到待評價土質邊坡Ni關于指標Ci的值Vi，邊坡 Ni的表示方式為

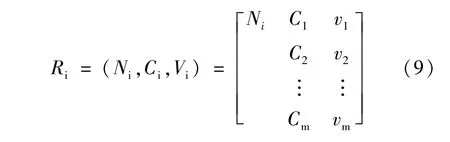
(3)單指標相關度:為表征同類中不同事物間的差異，在可拓理論中，規定 x0為區間長度，以ρ(x，x0)為距表示x與區間x0＝[a，b]之間的距離

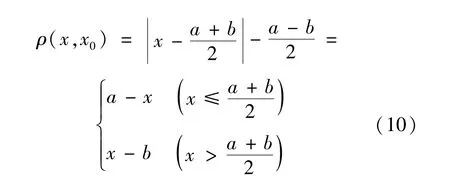
單指標相關度，即土質邊坡Ni第i個評價指標與等級s的相關性函數為:

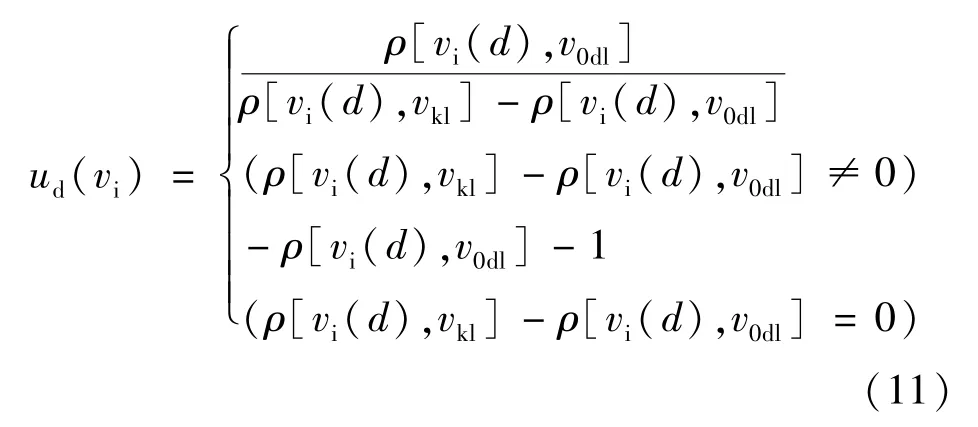
(4)綜合相關度和等級相關度:待評價土質邊坡Ni與等級s的綜合相關度為

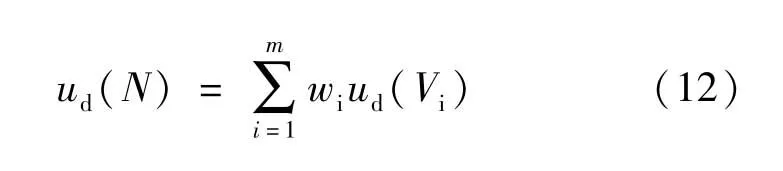
式中，wi為各指標權重，滿足

此外，為了便于比較及消除評價指標量值范圍的不對等所造成的影響，需要將us(N)進行標準化處理得到等級相關度:

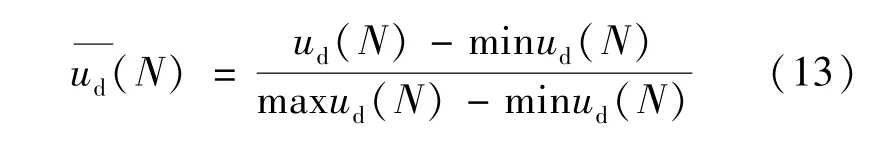
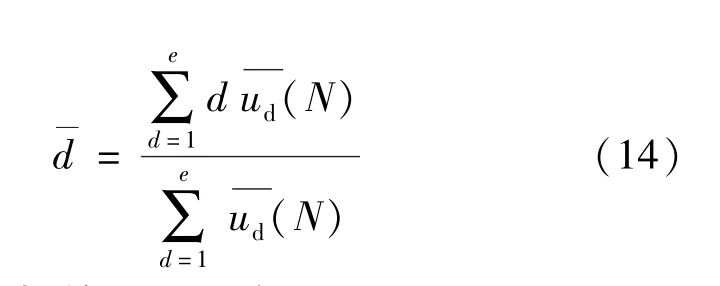
2.4.2 一級指標的可拓評價

將二級指標可拓評價所得到的等級特征值d作為進行一級指標可拓評價的取值。一級指標的穩定性等級仍為d個，取值范圍均勻劃為:(1，2)，(2，3)，…，(d，d ＋1)，若指標值超出范圍，則取最大值。其余計算與二級指標評價步驟相同。得出一級指標計算單指標相關度、綜合相關度及等級相關度后，便可確定邊坡的穩定性。

3 實例應用

3.1 工程概況

該邊坡高程300～380 m，自然坡度約25°～46°，局部較陡。滑坡所處地區為丘陵地貌，地表覆蓋層主要為第四系全新統沖積層的粗圓爍土、砂質黃土、塊石土以及第四系上更新統的風積砂質黃土，厚度為15～20 m。根據現場試驗與觀察，坡體上部土體結構松散，植被發育，有利于地表水向地下水下滲補給，坡體土含水量為18.77%，內摩擦角約為12°，黏聚力約為8 kPa，土體重度為24 kN/m3。重慶地區屬亞熱帶季風氣候，年均溫約18℃，年降雨量大于1 000 mm。重慶西站位于中國重慶市沙坪壩區，該地區抗震設防烈度為6度，設計基本地震加速度值為0.05 g。根據表3和式(5)、式(6)，得到該土質邊坡各評價指標值，見表5。

表5 邊坡穩定性評價指標取值

3.2 二級指標可拓評價

利用表4和表5中的評價指標值和表3中各指標權值及式(7)～式(11)，可得二級指標的單指標相關度、綜合相關度、等級相關度及一級指標值，見表6。

表6 _二級指標可拓評價結果

3.3 一級指標可拓評價

由以上計算可得，地形地貌V1、地質條件V2、氣象水文V3及地震V4的一級評價指標值分別為3.389、4.371、2.661和3.155。依照前文所定標準，將一級指標評價中的土質邊坡穩定性分為5個等級，取值范圍分別是[1，2)，[2，3)，[3，4)，[4，5)，[5，6]。其余步驟與二級指標評價的步驟一致，由此可得出該土質邊坡一級指標的單指標相關度、綜合相關度和等級相關度，見表7。

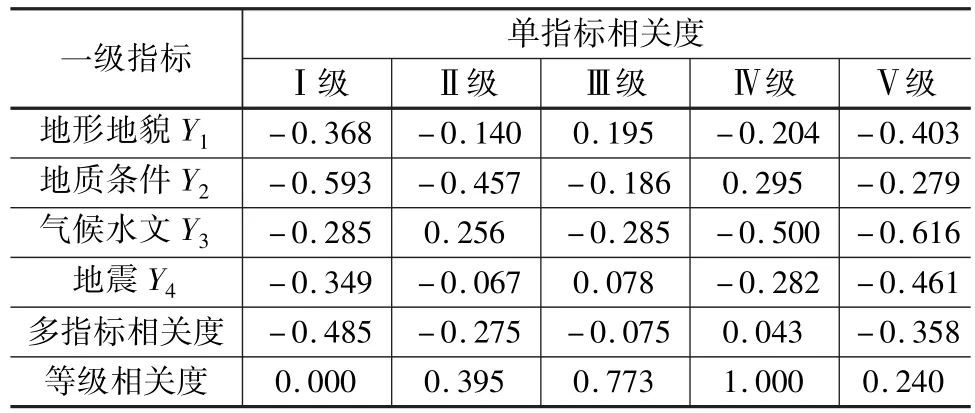
表7 一級指標可拓評價結果

從表7可得，該土質邊坡穩定程度與Ⅳ級相關度最大，即該邊坡穩定等級處于Ⅳ級，為不穩定狀態，這與現場由專家根據有限元法和赤平投影分析法得到該邊坡處于極限平衡狀態的結果相吻合。

4 結論

本文基于可拓學對鐵路樞紐土質高陡邊坡穩定性評價模型的研究，得到了以下結論:

(1)考慮地形地貌、地質條件、水文和地震4個方面的因素，選定土質高陡邊坡穩定性評價的8個指標建立評價體系，該指標體系可以較好地描述土質高陡邊坡特征，評價指標體系較為完整。

(2)采用基于OWA算子的賦權方法，計算過程簡便，且減少了由于專家偏好導致的極值對結果產生的不利影響，使評價結果更加客觀。

(3)將該模型應用至重慶西站擴能改造工程某土質高陡邊坡工點的穩定性評價之中，所得結果與有限元法和赤平投影分析法結果吻合，證明了本文提出模型的有效性，可以推廣到其他山區鐵路樞紐土質高陡邊坡工點的穩定性評價之中。