淺談初中數學建模課的開發與實施

于曉華

摘 要：數學建模已成為中小學數學學習的目標。在2011年版數學課程標準中把“數學建模”作為10個核心概念之一，明確指出模型思想的建立是學生體會和理解數學與外部世界聯系的基本途徑。教師如何更好地開展數學建模課？以《數學建模課之三角形數》為例，從建模課素材的開發、實施、流程等進行了簡明的說明。

關鍵詞：選擇素材;抽象建模;模型應用;模型再發現

隨著我國基礎教育課程改革的深入，數學建模活動已擴展到義務教育階段。數學建模已成為中小學數學學習的目標。學生不僅要學習數學知識，更要學習數學思想和方法，而數學模型是一種基本的數學思想，是解決數學問題的有效形式。學生親自經歷模型建立的“再創造”過程，有利于學生的多種感官參與，獲得豐富的感性認識，形成清晰表象，并有助于培養學生初步學會運用數學的思維方式去觀察和分析現實社會。

如何在中學階段開展數學建模活動？教師要選好素材，開發好的建模課，一是根據教學的情況，從教學及其相關內容的拓展中選取，使學生容易接受;二是根據教學的周邊實際環境尋找能使學生明白或通過比較簡單的觀察就能理解的問題。建立和求解模型的過程包括：從現實生活或具體情境中抽象出數學問題，用數學符號表示數學問題中的數量關系和變化規律，求出結果并討論結果的意義。

下面我以自己開發的一節七年級的數學建模課《數學建模課之三角形數》為例進行說明，引領七年級的學生熟悉建模的一般過程，也希望能對老師們有所啟發。

一、選擇素材

在日常生活中，我們發現保齡球、臺球的擺放、婚禮上香檳塔的擺放、工地上鋼管的擺放方式都基本相同，這里面是否蘊藏著一定的數學知識呢？選好素材，和學生一起研究，發現問題，提出問題。

圖片展示保齡球、臺球的擺放方式，經典誦讀比賽中班級的隊形，引發思考，它們擺放的共性是什么？

學生觀察圖片，上臺演示所站隊形，在觀察中感受生活中這類問題蘊含的數學知識。

二、抽象建模

1.從數、形兩個角度來感受認識模型：

形的角度：將班級隊形中每個人抽象成一個點，將這一定數目的點在等距離的排列下可以形成一個三角形，這樣的數可以稱為三角形數。

數的角度：像1、3、6、10、15…這些能夠表示成三角形的形狀的總數量的數，叫作三角形數。

2.用代數式表達第n個三角形數。

數的角度：首尾相加法

形的角度：圖形倒置相加法

學生經歷由特殊到一般和由一般到特殊的過程，體會代數推理的特點和作用。能用代數式表示并借用代數式運算驗證所探索規律的一般性。再一次滲透數形結合思想。

三、模型應用

問題1：數線段

1.觀察下面各圖，回答問題，將你的方法和大家交流。

圖①中有 1 條線段，

圖②中有 3 條線段，

圖③中有 6 條線段，

問題2：握手問題。參加一次聚會的每兩人都握了一次手，30人共握手多少次？

學生發現“三角形數”這個模型不僅僅存在于保齡球、臺球的擺放，在七年級剛學過的數線段和握手問題中同樣存在著它們的影子，不同的問題背景卻蘊含相同的數學模型，引領學生在問題解決過程中進一步體會數學的模型思想。

四、模型再發現

問題3：你能舉出幾個與三角形數有關的例子嗎？

學生展開想象，從課本到生活，枚舉了大量的實例：

如幾何問題：數線段、數角、直線相交最多的交點個數、直線分平面問題……

如代數問題：握手問題、循環賽問題、車站問題……

再如生活中婚禮上的香檳塔、飛機列隊表演、工地上的木樁擺放等等。

讓學生展開想象，實現三角形數這個模型的再發現，進一步領悟了數學的模型思想，增強了建模意識。

五、綜合拓展

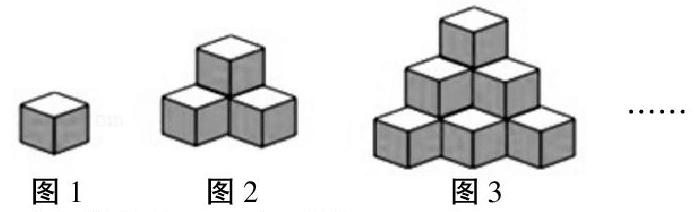
問題4：圖1、圖2、圖3是由棱長為1的正方體擺放而成的幾何體，按照這樣的方法繼續擺放，自上而下分別叫作第1層、第2層…第n層。

①上圖中你能發現三角形數嗎？

②請你就三角形數提個問題，交流并解決。

將三角形數進一步拓展，在發現中提出新的問題，實現知識的進一步提升。

以上就是《數學建模課之三角形數》的簡要剖析。數學建模是一個總的課題，初中數學教學中的建模要根據學生心理特征與認知水平，既有共性，又有個性。教師開發和實施數學建模課的出發點是：培養學生用數學的意識和觀念，遇到問題能從數學的角度去審視問題、觀察事物，闡釋現象、分析問題和解決問題。

參考文獻：

[1]張景斌，王尚志.中學數學建模活動為中學生創造發展空間[J].數學教育學報，2001（1）.

[2]王暢.新課程下中學數學建模活動的研究[D].湖南師范大學，2007.

編輯 郭小琴