改進的Holtrop船舶阻力估算

(南通中遠海運川崎船舶工程有限公司，江蘇 南通 226005)

目前，船舶阻力預報最精確的方法主要是船模試驗，船舶設計初期，在沒有型線的前提下，無法應用船模試驗和CFD仿真來確定阻力，一般采用近似的方法估算船舶阻力。近似估算阻力的方法有很多，這些估算方法雖然有著耗時少，成本低等優點，但是存在估算精度低，適用范圍有限等不足。改進的方法[1-5]雖探討了不同阻力估算公式，但適用范圍有限。為此，考慮從船舶設計者角度，尋求一種快速的、精度高的，以及適用范圍廣的預報方法。搜集30多艘三大主力船型的資料，形成船型數據庫。采用Holtrop方法分別對船型數據庫中的散貨船、集裝箱船、油船的阻力進行估算，通過數學統計分析，改進相關參數的經驗公式，提出一種輸入參數少，適用范圍廣以及估算精度高的阻力估算的半經驗公式。

1 Holtrop阻力估算公式

Holtrop法[6-7]其估算公式如下。

Rt=Rf(1+k)+Rapp+Rw+Rb+Rtr+Ra(1)

式中：Rf為摩擦阻力，根據ITTC1957公式得到；1+k為船舶形狀因子；Rapp為船舶附體阻力；Rw為興波阻力；Rb為球鼻艏引起的附加阻力；Rtr為方艉引起的附加阻力；Ra為船模與實船相關的修正因子。

Holtrop給出了式(1)中每個參數的回歸公式，綜合這些回歸公式，可以總結出其總阻力的一般函數表達式。

Rt=f(L,B,T,Δ,Cb，Cp，Cm，Lcb，ABT，hB，AT，SApp)

(2)

式中：L、B、T分別為船長、船寬、吃水；Δ為船舶的排水量；Cb、Cp、Cm分別為方形系數、棱形系數以及中橫剖面系數；Lcb為船舶浮心縱向位置；ABT、hB分別為球鼻艏橫向面積和球鼻艏橫截面中心高度；AT為艉封板浸水面積；SApp為附體濕表面積。

采用Holtrop公式對船型數據庫中的船舶進行阻力估算，并與試驗值進行對比，誤差分布見圖1。

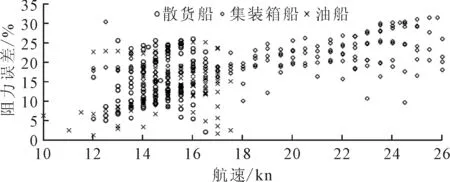
圖1 三大主力船型Holtrop法阻力估算誤差分布

由圖1可見，Holtrop法估算船舶阻力的誤差較大，大部分在10%～30%之內。其中散貨船和肥大型油船的阻力誤差相對較小，部分誤差在10%以下；集裝箱船的阻力誤差較大，基本在15%以上。從航速上來看，速度較低時，阻力誤差相對較小，當速度增加時，阻力誤差隨之增大。

2 改進Holtrop阻力估算公式

Holtrop公式采用三因次法估算船舶的阻力，除了黏性阻力和興波阻力外，還考慮了球鼻艏、方尾、附體引起的附加阻力以及船模與實船的尺度效應，輸入變量較多，對于不同船型，其阻力估算的誤差有一定的差別。在船舶設計初期，已知的主要參數有限，尤其是球鼻艏、方尾以及附體的參數無從得知，很難利用公式進行估算。鑒于此，分別對球鼻艏、方尾以及附體引起的附加阻力進行討論，在保證精度的前提下，尋求一種可靠的替代方案。

1)球鼻艏引起的附加阻力Rb。采用球鼻艏對于某些船型可以有效降低船舶的興波阻力，這部分的阻力變化在興波阻力中已經考慮，而由球鼻艏本身引起的附加阻力較球鼻艏減阻效果為小量，可放到船模與實船的修正因子Ca中考慮。另外，Holtrop公式中也對球艏重心高度作了限制，不能超出0.6Tf(艏吃水)，而球艏的重心普遍較高，限制了Rb的計算。

2)方艉引起的附加阻力Rtr。對于低速船，方艉處會形成漩渦，對阻力不利，這方面的影響可在船舶形狀因子K中考慮；對于中高速船，方艉會增加船舶的虛長度，一定程度上將降低船舶的阻力，這方面的影響可在船模與實船的修正因子Ca中考慮。

3)附體阻力Rapp。附體對阻力的影響為小量，主要影響船舶的推進性能，因此，附體對阻力的影響可在船模與實船的修正因子Ca中考慮。

綜合上述分析，對Holtrop公式進行一定的簡化，將球鼻艏、方艉,以及附體阻力的影響考慮到船模與實船的修正因子中，得到船舶總阻力系數為

Ct=Cf(1+K)+Cw+Ca

(3)

式中：Cf為摩擦阻力系數，采用ITTC1957公式；Cw為興波阻力系數；K為船舶形狀因子；Ca為船模與實船的修正因子。

主要輸入參數見表1。

表1 主要的船型參數

注：在船舶設計初期，不考慮有縱傾的工況；海水密度取常數，即1.025 kg/m3。

式(2)中的方形系數、棱形系數和中橫剖面系數，采用表1中已知的參數計算得到。其中中橫剖面系數Cm，可以考慮扣除中橫剖面處舭部圓弧(一般圓弧半徑為1.8 m)的面積近似估算得到。

Holtrop公式中沒有涉及對浮心縱向位置Lcb的估算，Lcb的值對摩擦阻力的影響較小，但是其值會影響船體的艏部和艉部形狀，進而影響船舶的興波阻力和黏壓阻力。根據已有船型數據庫，總結Lcb與Cb的關系，見圖2。

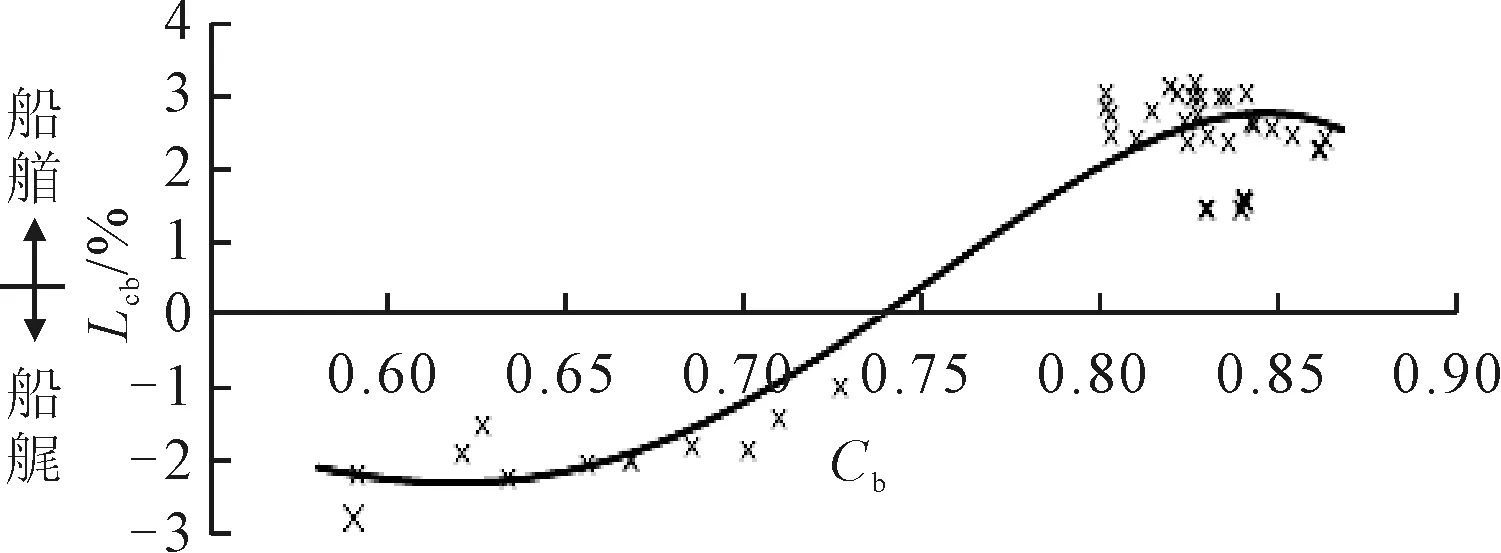
圖2 浮心縱向位置隨方形系數變化規律

根據圖2，擬合Lcb的估算公式如下。

2 563.3Cb-387.63

(4)

Holtrop公式中給出的濕表面積公式如下。

0.286 2Cm-0.003 467B/T+

0.369 6Cwp)+2.38ABT/Cb

(5)

對數據庫中的數據進行擬合，在式(5)的基礎上進行修改，得到濕表面積估算公式如下。

Smod=L(2T+B)(0.623 5+0.333 2Cb-

0.002 611B/T)+BL(0.264 1Cb-0.261 3)

(6)

運用式(5)和式(6)估算數據庫中三種主力船型的濕表面積，并與實際值進行對比，見圖3。

圖3 兩種方法估算不同船型濕表面積誤差對比

由圖3可見，由式(6)估算得到的濕表面積的誤差明顯降低。

對于形狀因子，Holtrop方法中給出了1+K的估算公式。

1+K=0.93+0.487 118c14(B/L)1.068 06·

(T/L)0.461 06(L/LR)0.121 563·

(L3/▽)0.364 86(1-Cp)-0.604 247

(7)

式中：LR為Holtrop公式中定義的船型因子，與L、Cp、Lcb有關。運用式(7)對現有船型的形狀因子進行估算，并與數據庫中的數據進行對比。通過分析對比，修改式(7)，得到改正后的形狀因子公式如下。

1+Kmod=1.046 6+0.312(B/L)1.068 06·

(T/L)0.461 06(L/LR)0.121 563·

(L3/▽)0.364 86(1-Cp)-0.604 247

(8)

興波阻力估算仍采用Holtrop法中給出的公式。式(3)中并未單獨考慮球艏、方尾、附體等的影響，而是將這些影響放到了船模與實船的修正因子Ca中。通過對比改進后的經驗公式和船型數據庫中船舶試驗結果，發現Ca的值不僅與船長和船速有關，還與船型有關。根據水池試驗的結果和式(3)，回歸分析得到不同船型修正因子Ca的關系。

1)集裝箱船(R2=0.83)。

Ca×103=-0.434 2-13.61Fr2+

1.858Fr+125.6/L

(9)

2)散貨船(R2=0.71)。

Ca×103=0.256 1-26.06Fr2+

0.800 6Fr+47.95/L

(10)

3)油船(R2=0.69)。

Ca×103=-1.482-65.07Fr2+

18.11Fr+109.9/L

(11)

式中：Fr為弗勞德數；R2為回歸系數，表示模型擬合度的好壞，其值越接近1，說明擬合效果越好，從回歸系數可以看出，回歸公式的擬合度較好。

3 改進的船舶阻力公式驗證

為進一步驗證上述公式的精度及適用性，以不屬于船型數據庫中的3艘主力船為例，采用上述改進的半經驗公式進行估算船舶的阻力。3艘船的主要參數見表2。估算結果見表3～5。

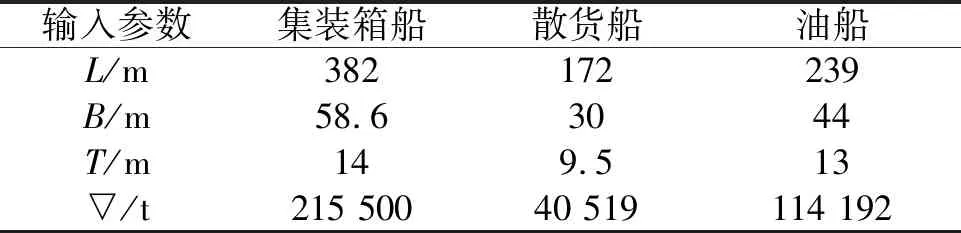
表2 三種主力船型基本參數

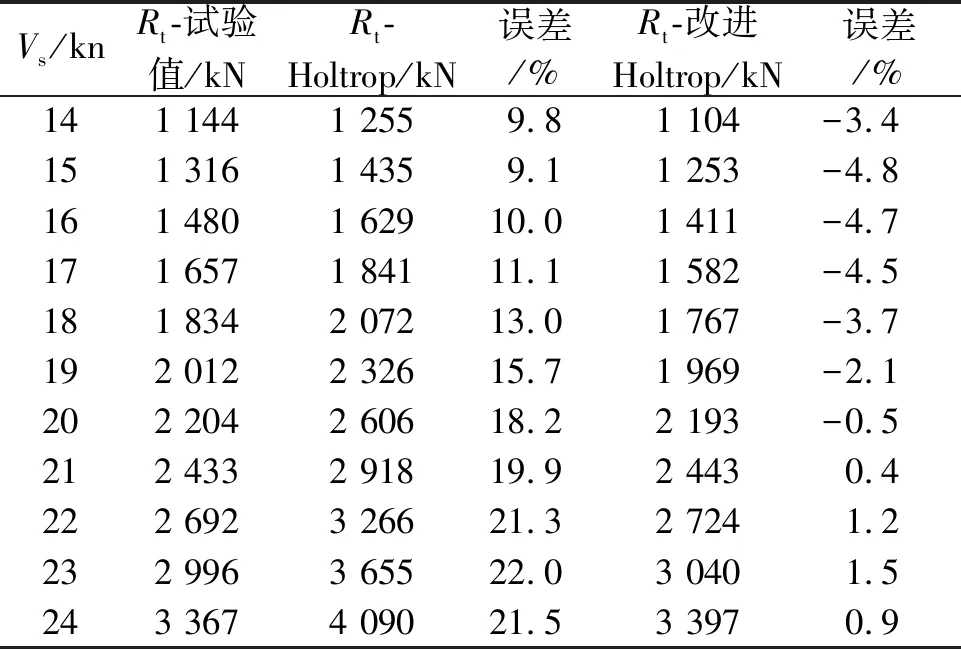
表3 集裝箱船阻力估算值與試驗值對比

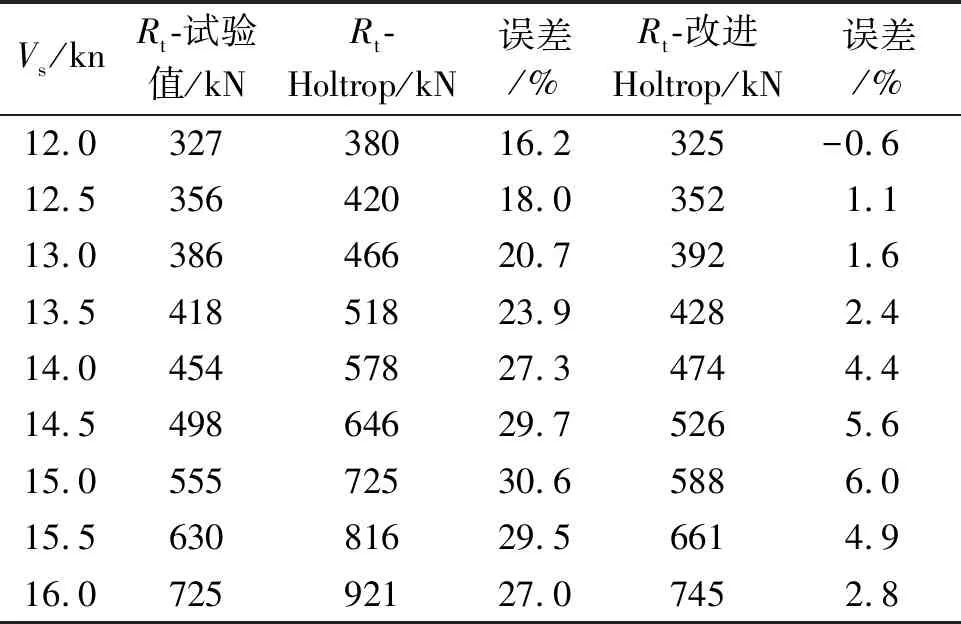
表4 散貨船阻力估算值與試驗值對比

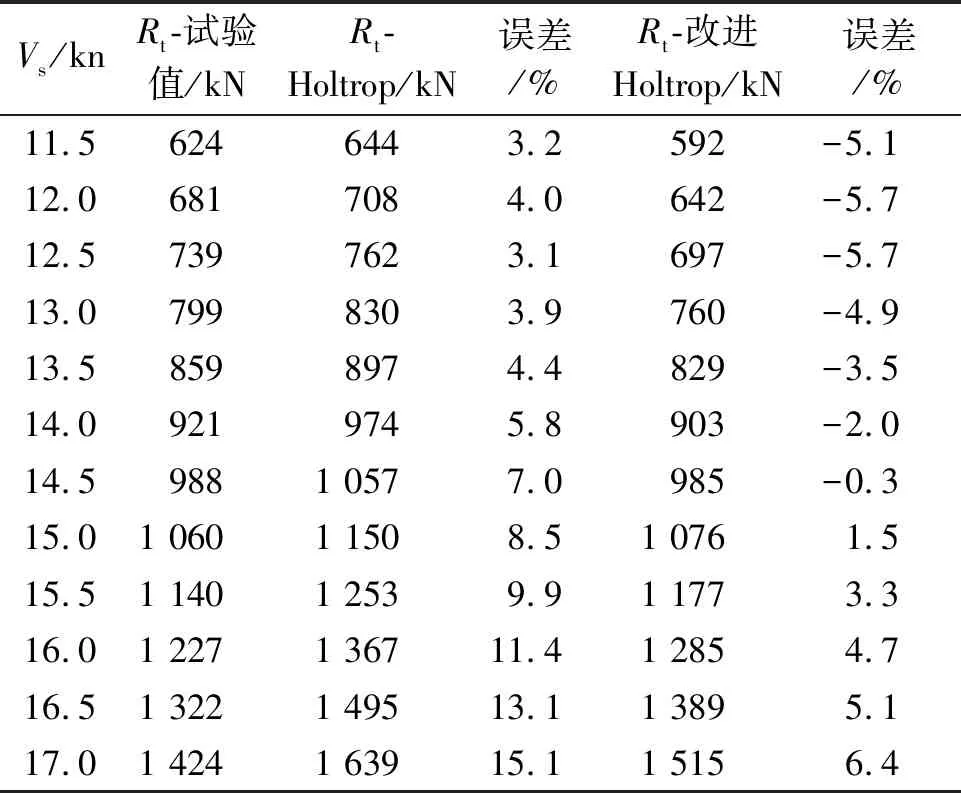
表5 油船阻力估算值與試驗值對比

由表3～5可見，改進后的Holtrop法估算結果對3種主力船型都有很好的適用性，并且誤差也得到改善，均在7.0%以內，達到一定的修正效果。

4 結論

通過對比現有新造船的船型數據庫，基于三大主力船型的試驗數據，對Holtrop法中部分公式進行改進，修正船模與實船相關因子，并減少該方法的輸入參數。經過驗證，采用改進的方法，3種船型的阻力估算值的精度明顯得到提高，具有一定的工程應用價值。

將已有的估算公式與已建造船的數據結合起來，通過總結和歸納的方法，尋求適合新造船阻力估算的方法，在船舶設計初期不失為一種有效的阻力估算方法。鑒于本文的船型數據庫樣本容量有限，統計公式仍需進一步完善。另外，本文僅分析了阻力的估算方法，對推進方面的歸納還需進一步探討。