直線(xiàn)定比分割在建筑制圖中的應(yīng)用研究

肖昕迪 袁玲

摘要：有節(jié)奏變化構(gòu)件的建筑施工圖和透視圖手工繪制時(shí)，構(gòu)件尺寸定量需要反復(fù)操作，過(guò)程較為繁瑣，但是采用直線(xiàn)定比分割的方法繪制，事半功倍.本文從直線(xiàn)定比分割理論著手，介紹了其在建筑施工圖和透視圖中的應(yīng)用方法，以及比值為無(wú)理數(shù)時(shí)的應(yīng)用方法.

關(guān)鍵詞：定比分割;建筑制圖;樓梯施工圖;透視圖

中圖分類(lèi)號(hào)：O185.2? 文獻(xiàn)標(biāo)識(shí)碼：A? 文章編號(hào)：1673-260X（2019）07-0020-03

建筑圖樣是建筑工程行業(yè)交流的必需工具，在其它相關(guān)領(lǐng)域中也有著非常廣泛的應(yīng)用.隨著計(jì)算機(jī)繪圖軟件的發(fā)展，計(jì)算機(jī)取代了大部分的手工制圖內(nèi)容，但手工制圖在繪制效果圖、透視圖、以及小項(xiàng)目施工圖時(shí)，更為快捷.尤其是對(duì)于初學(xué)者來(lái)說(shuō)，手工制圖入門(mén)較低，更容易掌握?qǐng)D樣中的相關(guān)標(biāo)注和規(guī)定，在其表達(dá)方案時(shí)更簡(jiǎn)單快捷[1]，也是計(jì)算機(jī)制圖的必需基礎(chǔ)[2].另外，設(shè)計(jì)人員構(gòu)思和方案交流時(shí)，手工制圖使思維和手眼之間以白紙黑線(xiàn)條的效果呈現(xiàn)得更流暢，操作也更為靈活[3].然而，手工繪圖時(shí)常常遇到較為繁瑣的、難以控制的尺寸定量繪制，如樓梯臺(tái)階等有節(jié)奏變化形體的施工圖、透視圖.直線(xiàn)定比分割在數(shù)學(xué)領(lǐng)域中是個(gè)較為簡(jiǎn)單的基礎(chǔ)解題方法，對(duì)建筑制圖中，對(duì)有節(jié)奏變化形體的施工圖和透視效果圖采用直線(xiàn)定比分割的方法，事半功倍.

1 直線(xiàn)定比分割理論

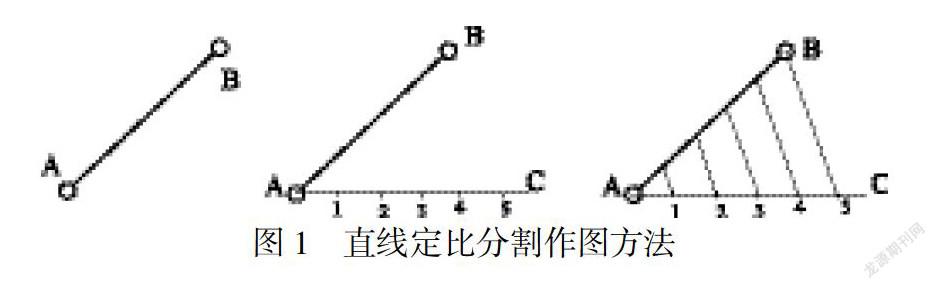
如圖1，五等分直線(xiàn)AB，需以直線(xiàn)端點(diǎn)A或者端點(diǎn)B為頂點(diǎn)，做一條射線(xiàn).在射線(xiàn)上從頂點(diǎn)位置起，取五等份，并依次編注各分點(diǎn)：1、2、3、4、5，連接B5.然后過(guò)其他分點(diǎn)分別做直線(xiàn)平行B5，形成平行直線(xiàn)組，并交AB于四個(gè)點(diǎn)，即為所求[4].

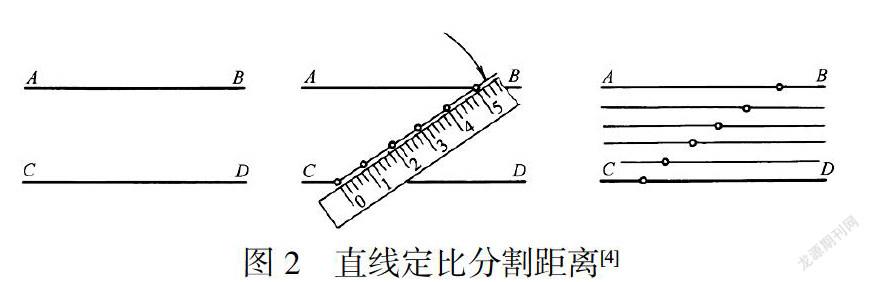
平面圖形中的距離等分也可以用此方法，如下圖2圖中的兩平行線(xiàn)之間的距離等分.放直尺于兩線(xiàn)之間，按等分份數(shù)來(lái)選擇其整倍數(shù)的刻度，并畫(huà)出一直線(xiàn)做等分，取得各分點(diǎn)后，過(guò)個(gè)分點(diǎn)作兩直線(xiàn)的平行線(xiàn)，即把兩平行線(xiàn)間距離等分.

這種等分兩平行線(xiàn)間距離的方法，在建筑施工圖中可運(yùn)用于樓梯平面圖、剖面圖的作圖中.

2 在建筑施工圖中應(yīng)用

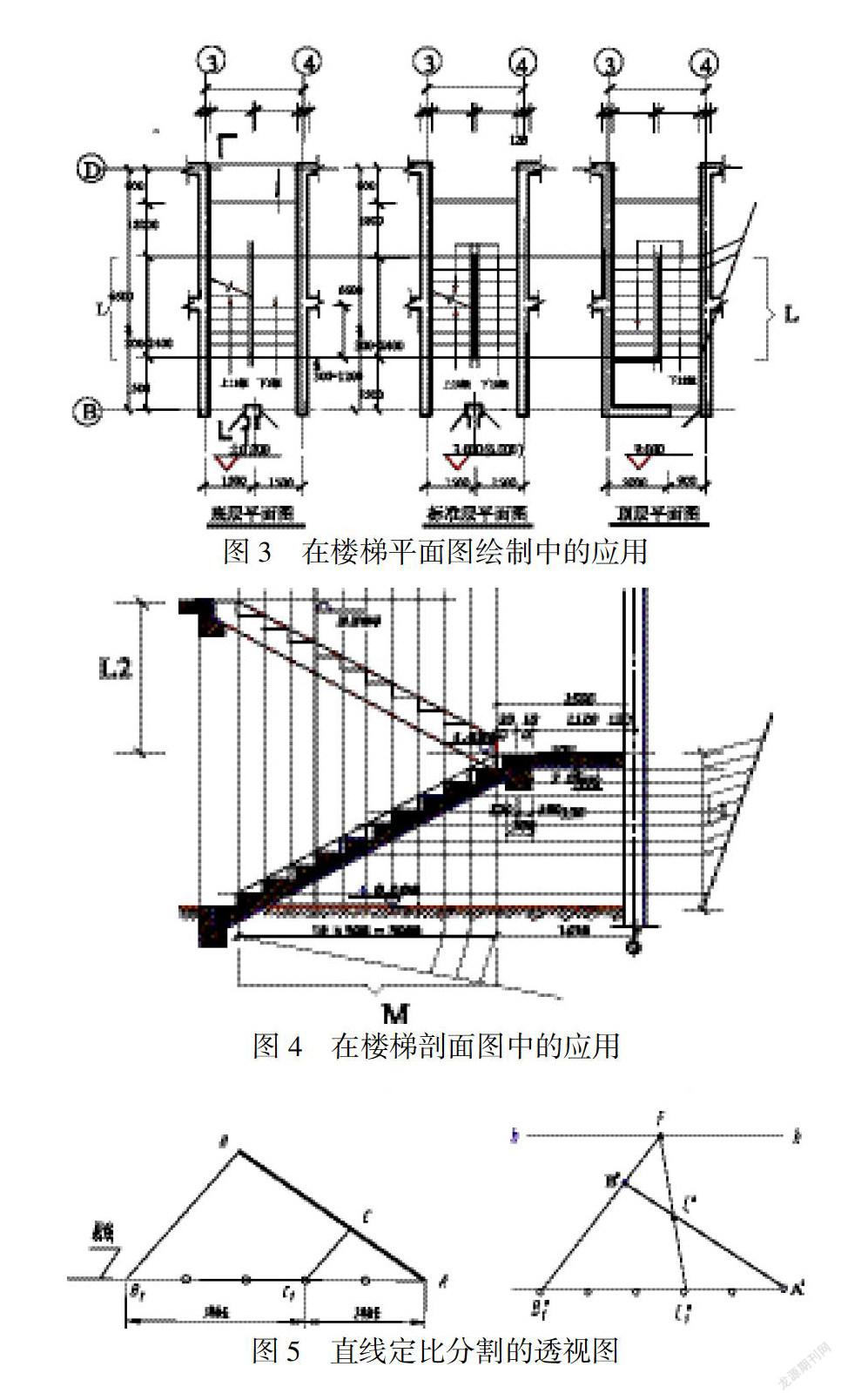
在繪制建筑施工圖中的樓梯平面圖和剖面圖時(shí)，操作工序較瑣碎，圖樣繪制較耗時(shí)，每個(gè)臺(tái)階都需要逐一定位后方可繪制.如果才用直線(xiàn)定比分割的辦法，事半功倍.如圖3，定位每個(gè)踏步時(shí)，只需要等比分割樓梯段的長(zhǎng)度L即可.

除此之外，還有在樓梯立面圖繪制時(shí)的應(yīng)用.在繪制每個(gè)臺(tái)階時(shí)，可先定位高度方向.如圖4所示，把樓梯高度分段為L(zhǎng)1、L2，分別對(duì)L1、L2進(jìn)行等比分割，取得各分點(diǎn)后做定位軸線(xiàn)B、D軸的平行線(xiàn);再把樓梯段的水平長(zhǎng)度M做定比分割，取得各分點(diǎn)后做平行直線(xiàn)組.此兩種方向各平行直線(xiàn)組相交即得出樓梯臺(tái)階位置圖，再按照相關(guān)國(guó)標(biāo)規(guī)定繪制圖例和標(biāo)注，即繪制出樓梯剖面圖.

3 在透視圖中的應(yīng)用

在透視圖中，除畫(huà)面上的圖形元素，其他與實(shí)際形狀和正投影形成的視圖相比，都發(fā)生了不同程度的變形.在手工制圖時(shí)準(zhǔn)確、快速地繪出各元素的透視一直圖學(xué)界探討的問(wèn)題.下面以樓梯臺(tái)階的透視圖為例，以直線(xiàn)定比分割來(lái)探討其簡(jiǎn)捷的繪制方法.

3.1 透視圖中直線(xiàn)定比分割的可行性

由圖1、圖2、圖3、圖4可知，直線(xiàn)的定比分割在繪制構(gòu)件的投影視圖中較為快捷，主要通過(guò)輔助射線(xiàn)上的分點(diǎn)做平行直線(xiàn)組的方法交于被分割的直線(xiàn)上來(lái)取得各分點(diǎn).輔助射線(xiàn)與被分割直線(xiàn)的關(guān)聯(lián)為連接二者分點(diǎn)之間的平行直線(xiàn)組，而這些平行直線(xiàn)組中的各直線(xiàn)必平行.透視圖中，相互平行的直線(xiàn)共滅點(diǎn)[5][6].如圖5，分割直線(xiàn)AB為2：3，其分線(xiàn)BB1∥CC1，則透視圖中，BOBO1與COC1O有共同的滅點(diǎn)F.由于AB1與AB分點(diǎn)之間的連線(xiàn)在空間中互相平行，在透視圖中共滅點(diǎn)，在透視圖中可按分線(xiàn)共滅點(diǎn)的方法進(jìn)行定比分割.

3.2 透視圖中直線(xiàn)定比分割的應(yīng)用

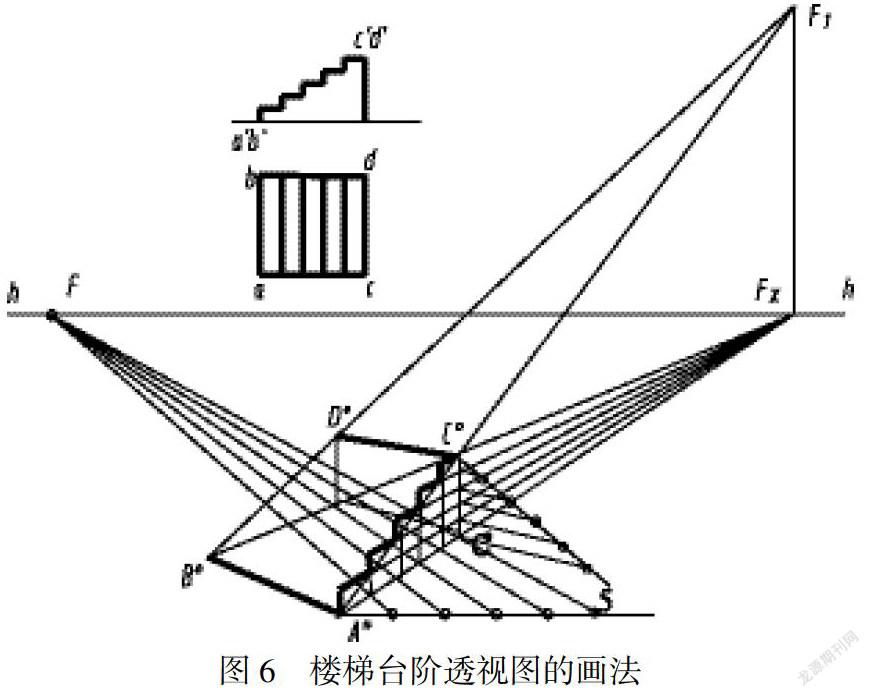
例如樓梯的兩點(diǎn)透視圖的繪制，對(duì)于各臺(tái)階的透視定位，如果逐一求解各個(gè)臺(tái)階上直線(xiàn)節(jié)點(diǎn)，不僅工作量巨大，輔助線(xiàn)也會(huì)增多，最終將會(huì)因作圖線(xiàn)條過(guò)多導(dǎo)致無(wú)法完成完整的透視圖.但是采用直線(xiàn)定比分割的辦法，分割臺(tái)階梯段高度Cc透視和斜線(xiàn)Ac透視，將會(huì)把作圖過(guò)程簡(jiǎn)化.如圖6.其過(guò)程如下：

（1）按照透視圖的求解方法，求出AC的透視AOCO和基透視AOco.

（2）以圖1的方法在空間中分割A(yù)c五等份.此時(shí)做的射線(xiàn)A5必須在畫(huà)面上或者為基線(xiàn)平行線(xiàn).取得分點(diǎn)后，利用“相互平行的直線(xiàn)共滅點(diǎn)”、以及“基面上的線(xiàn)透視滅點(diǎn)在視平線(xiàn)上”[5][6]的理論，如圖5的做法，推理出5co的滅點(diǎn)F即為AOco與Ao5分點(diǎn)5條連線(xiàn)的滅點(diǎn)，由此可在透視圖（圖6）中分割A(yù)Oco.

（3）由F點(diǎn)連接Ao5上的各分點(diǎn)，交于AOco上四點(diǎn)，這四個(gè)點(diǎn)即為Ac線(xiàn)段上的五分點(diǎn)的透視.由此四分點(diǎn)的透視做鉛垂線(xiàn)交于AOCO，即求出AC的五等分點(diǎn)的透視.

（4）由于Cc是平行于畫(huà)面的鉛垂線(xiàn)，“畫(huà)面平行線(xiàn)的透視與其本身平行，且成比例”[4]，Coco的等分可直接采用圖1的方法進(jìn)行分割，并得出四個(gè)等分點(diǎn).

（5）由Coco的等分點(diǎn)連接滅點(diǎn)FX并反向延長(zhǎng)，分別與AOCO的各分點(diǎn)透視相交，即能繪出AC間個(gè)臺(tái)階的透視圖.再以F滅點(diǎn)連接各臺(tái)階折點(diǎn)，即能完整繪出臺(tái)階的透視圖.

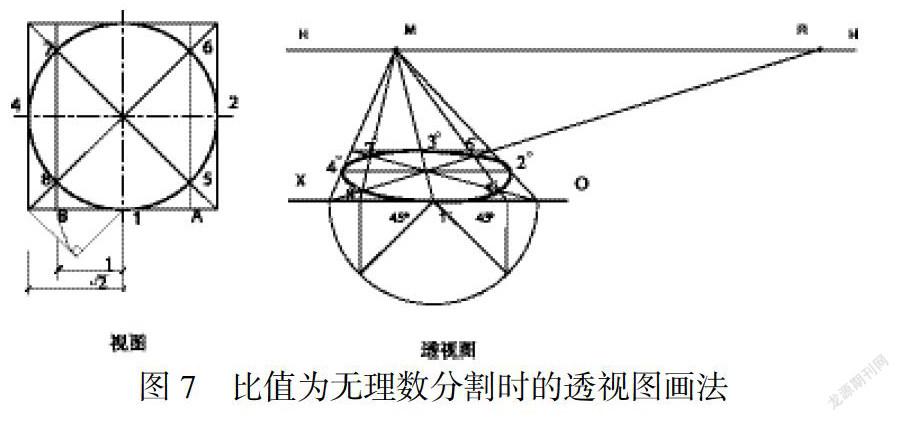
4 比值為無(wú)理數(shù)的應(yīng)用

以上的內(nèi)容都是在對(duì)線(xiàn)段整數(shù)分割時(shí)較為有利，對(duì)于比值為無(wú)理數(shù)分割時(shí)，就很難按這些方法操作，但可以構(gòu)建直角三角形，采用比例轉(zhuǎn)移的方法進(jìn)行分割.如圖7，水平圓的透視作圖.

對(duì)于圓的透視圖和軸測(cè)圖建筑制圖中常常采用的畫(huà)法為“八點(diǎn)法”，即通過(guò)求解圓周上八個(gè)點(diǎn)的投影位置，來(lái)定圓的投影形狀.此八點(diǎn)分別為圓外接正方形上的四個(gè)切點(diǎn)、外接正方形對(duì)角線(xiàn)與圓周的四個(gè)交點(diǎn)，如圖7.

從視圖中可知，四個(gè)切點(diǎn)1、2、3、4的位置均在正方形四個(gè)邊的中點(diǎn)上，在透視圖中，由于直線(xiàn)24平行于畫(huà)面，可過(guò)對(duì)角線(xiàn)交點(diǎn)做平行于基線(xiàn)OX的平行線(xiàn)和過(guò)對(duì)角線(xiàn)交點(diǎn)連接滅點(diǎn)M的方法，分別交于四邊1o、2o、3o、4o，即為1、2、3、4點(diǎn)的透視.

視圖中的另外5、6、7、8四個(gè)點(diǎn)位于各段對(duì)角線(xiàn)1：的分點(diǎn)處，可通過(guò)在直線(xiàn)1B上構(gòu)建等腰直角三角形的方法來(lái)分割.具體作圖過(guò)程為：以1點(diǎn)為圓心，以直角邊長(zhǎng)為半徑畫(huà)弧交出BD點(diǎn)，過(guò)B點(diǎn)做直線(xiàn)平行于正方形左側(cè)邊，交于對(duì)角線(xiàn)上的7、8點(diǎn).右側(cè)5、6點(diǎn)與7、8點(diǎn)可直接對(duì)稱(chēng)繪制出即可.由于直線(xiàn)56、78與兩側(cè)邊平行，在透視圖中共滅點(diǎn).由于直線(xiàn)AB在畫(huà)面上且與基線(xiàn)重合，其上的分割比例不發(fā)生改變，所以可直接以1B所在半段邊長(zhǎng)、1A所在半段邊長(zhǎng)構(gòu)建等腰直角三角形，分割出1：的分點(diǎn)，過(guò)分點(diǎn)作直線(xiàn)連接正方的的滅點(diǎn)，與對(duì)角線(xiàn)的交點(diǎn)即為5o、6o、7o、8o.如此，八個(gè)點(diǎn)的透視均已求出，按順序用光滑的曲線(xiàn)連接即可求出圓的透視.

5 總結(jié)

本文基于直線(xiàn)定比分割方法分析了在建筑圖樣應(yīng)用的三種情況，在繪制定比變化的形體圖樣時(shí)較為快捷，使復(fù)雜的樓梯平、剖面圖繪制過(guò)程簡(jiǎn)單化.并針對(duì)透視圖中對(duì)直線(xiàn)分割的應(yīng)用做了探討，另分析了直線(xiàn)分割比值為無(wú)理數(shù)時(shí)，采用構(gòu)建直角三角形的方法轉(zhuǎn)移比例的應(yīng)用技巧.

參考文獻(xiàn)：

〔1〕于習(xí)法，易素君，孫霞，張莉.兩點(diǎn)透視圖的一種畫(huà)法和透視圖尺設(shè)計(jì)的研究[J].工程圖學(xué)學(xué)報(bào)，2008（05）：121-124.

〔2〕張學(xué)炯.機(jī)械手工制圖準(zhǔn)備及錯(cuò)誤分析[J].科技視界，2019（03）：132-133.

〔3〕邱冰，張帆.以理想角度作兩點(diǎn)透視圖的一種簡(jiǎn)畫(huà)法[J].圖學(xué)學(xué)報(bào)，2012，33（06）：140-145.

〔4〕何斌，陳錦昌，陳熾坤.建筑制圖[M].北京：高等教育出版社，2005.

〔5〕鄧學(xué)雄，江曉紅，等.建筑圖學(xué)[M].北京：高等教育出版社，2015.

〔6〕吳機(jī)際.園林工程制圖[M].廣州：華南理工大學(xué)出版社，2016.