中國經濟增長與結構變遷的時變關系研究

李瑞杰

通過構建經濟總量增長速度的部門離散系數，作為經濟結構變遷系數，描繪中國經濟結構變遷過程，并建立線性非時變參數方程，定量研究經濟增長與結構變遷的相關特征，結果顯示：二者存在顯著正相關關系，但具有時變特征。進一步建立時變參數的狀態空間方程，考察經濟增長與結構變遷的時變關系特征，結果發現，1979—1997年二者相關關系處于低彈性、高波動的成長期；1998—2016年二者相關關系處于高彈性、平穩化的成熟期。中國經濟新常態下，政府應努力恢復經濟增長樂觀態勢，為結構調整提供寬松的彈性空間，實施更加“有為”的結構調整政策，加快產業結構高級演化。

一、引言

新中國成立以來，中國經濟在極度落后條件下實現經濟起飛，初步建立起獨立、完整的工業體系，進入現代經濟增長的準備階段。改革開放后，中國經濟進入高增長—高收入—高積累—高投資—高增長的良性循環，成長為世界第一工業大國（產業規模角度）。將時空劃定在中國改革開放至今，經濟高增長和經濟結構高變動無疑是中國最顯著的兩個現代經濟增長特征。

1978年以來，中國經濟增長取得了舉世矚目的成就，1978—2016年中國經濟實際年均增長率9.58%。尤其是進入21世紀的前十年，隨著中國特色社會主義市場經濟體制的建立與完善、經濟全球化進程不斷推進，中國經濟實際年均增長率高達10.55%，創造了世界經濟增長史的持續高增長神話。在高速增長的同時，也不可避免地經歷經濟增長波動：在經歷1982—1990年、1991—2001年兩輪完整的波谷—波谷的朱格拉周期后，中國經濟自2002年開啟經濟擴展趨勢，于2007年攀升至波峰。之后，在美國次貸危機的外部沖擊下，中國經濟進入經濟周期收縮階段，在2009年首次觸底反彈后，于2012年轉入經濟中高速增長新階段（見圖1）。

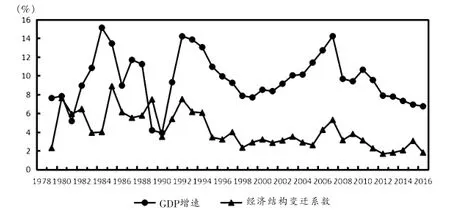
圖1 中國經濟波動與經濟結構變遷

中國在極端貧困落后的條件下，通過計劃經濟體制支持工業非平衡增長，建立起超常規產業格局。改革開放以后，在中國經濟高速增長的背景下，中國產業結構變遷以部門非均衡增長為前提快速推進，從工業化初期順利過渡到工業化后期。1978—2016年，中國第一產業增加值比重幾乎呈直線狀從27.7%下降至8.6%；第二產業增加值比重在小振幅波動中從47.7%下降至39.9%；第三產業增加值比重在波動中快速從24.6%上升至51.6%，中國產業結構經歷了較大程度和較快的變動（見圖2）。

圖2 中國三次產業增加值占比變動趨勢

經濟增長與結構變遷作為描述中國現代經濟增長過程的兩條主線，并不是相互獨立的兩條平行線，而是具有緊密內在交互關系的兩條線。如圖1，經濟增長和經濟結構變遷都具有明顯的波動特征，且二者波動具有一致性：當經濟開始擴張時，經濟結構變遷系數①開始擴大；當經濟轉入收縮階段，經濟經濟結構變遷系數也開始回落；經濟波動和經濟結構變遷的緩和化趨勢高度一致。聯想到菲利普斯曲線中的經濟增長率和通貨膨脹率之間的替換關系，在經濟增長與經濟結構變遷之間是否也存在類似置換關系②，這是本文要解決的問題。

二、相關文獻綜述

（一）經濟發展過程中的經濟結構演變規律

現代經濟增長理論則始于19世紀40年代。哈羅德—多馬（Harrod-Domar）模型的出現掀起現代經濟增長理論的第一波浪潮。幾乎同時，Clark首先刻畫出經濟發展與經濟結構演變的歷史關聯，形成經典的配第—克拉克定理［1］。而發生這種變動的原因是，產業部門相對收入伴隨經濟總量增長不斷發生變化。即產業部門的相對收入差距直接導致了勞動力結構的演變。自此，經濟增長和結構變遷一直備受學界關注。在Clark的研究基礎上，Kuznets改善研究方法，對經濟增長與結構變換的歷史關聯進行細化研究：在研究經濟增長過程中的產業結構變動規律時，同時考慮勞動力結構和部門產值結構變動。運用比較勞動生產率來作為產業部門相對收入指標，認為比較勞動生產率變化是產業結構演變的直接原因，并進一步探討了比較勞動生產率變化的驅動力量。［2］Chenery認為世界范圍內經濟活動基本要素的趨同，導致存在某種更具普遍意義的現代經濟增長模式演變過程。［3］他吸取Clark和Kuznets研究成果，擴展研究對象和時間跨度，將生產、需求、貿易、資源使用和人口納入經濟結構演變分析框架，研究1950—1970年間101個國家（地區）的經濟結構演變過程，得出具有一般意義的“標準結構”。Chenery認為經濟結構變動受到收入水平、資源稟賦、人口規模、國家政策以及國際貿易等影響。

（二）經濟增長與結構變遷交互作用的傳導機制

經濟增長與結構變遷交互作用的橋梁是技術進步，Kuznets和Baumol首先對此做了系統性研究。Kuznets對技術革新下的經濟高增長率與產業結構的高變換率雙向傳導機制作出詳細闡述，并結合供需兩端給出了三條傳導路徑：封閉經濟條件下，當科技大規模應用于生產帶來經濟的持續高速增長，導致需求結構的快速變動，最終帶來產業結構的高變換率；開放經濟條件下，各國經濟發展水平、增長速度差異較大的背景下，各國之間的貿易往來會促使一國的產出結構變動；技術革新推動經濟增長的過程是具有特定路徑的，它首先出現在少數行業，形成技術革新中心。技術革新中心的不斷轉移推動經濟結構的轉變。結構變遷到經濟增長的傳導機制則是，生產結構的改變間接造成生活水平的提高，創造出新的消費需求，進一步刺激到技術革新的產生，最終推動經濟增長。［2］Baumol在技術進步視角下，從供給端對經濟增長和經濟結構變遷的關系進行研究。［4］他將經濟部門分成先進部門和非先進部門，構造出兩部門非平衡增長模型。在要素跨部門自由流動前提下，技術革新會打破原有經濟平衡狀態。先進部門生產率的較快提高，會導致非先進部門的成本和價格的不斷上升，陷入“鮑莫爾成本病”（Baumol’s disease）。Baumol還認為生產部門非均衡增長引起的經濟結構變化，可能會對整體經濟增長產生負向影響。Ngai在Baumol兩部門非均衡增長模型基礎上，構建了多部門經濟增長模型。［5］他認為，各部門的技術進步水平差異直接決定了部門全要素生產率差異，全要素生產率的部門差異引起勞動和資本生產要素的定向流動，最終導致了經濟結構變化。值得注意的是，Ngai認為這種經濟結構變遷并不會阻礙總體經濟增長，Baumol的“結構負擔假說”是不成立的。

（三）經濟增長與結構變遷交互作用實證研究

在經濟增長與經濟結構變遷傳導機制的研究基礎上，中外學者從實證研究層面對經濟增長與結構變遷的單向或雙向關系做了大量研究。蔣振聲運用中國1952—1999年相關數據，較早地對中國經濟增長與結構變遷之間的關系進行了實證分析。［6］證實中國經濟增長與結構變遷之間存在長期穩定相關關系，產業經濟結構變遷能顯著推動經濟增長，而經濟增長對經濟結構變遷的影響并不顯著。通過文獻梳理發現，隨著研究的深入，實證研究重點轉向結構變遷對經濟增長的單向推動作用，即圍繞“結構紅利”的證實與證偽展開。在研究方法層面存在兩種主要思路：第一，將經濟結構變遷和經濟增長指標化，建立線性方程或者脈沖響應函數，定量考察其交互關系的總體特征或者時變特征。干春暉運用中國1978—2009年30個地區的面板數據，以產業高級化指標（第三產業與第二產業產值之比）和產業合理化指標（泰爾指數）作為衡量產業結構變遷的指標，以實際經濟增長率作為經濟增長指標，構建非時變線性模型，通過分時段回歸，發現產業結構合理化與高級化進程都會對經濟增長產生正向作用，但這種正向作用具有明顯的階段特征。［7］第二，運用偏離—份額法（Shift-share Method）研究由要素流動帶來的產業結構變遷對要素生產率或經濟增長的影響。劉偉運用中國1978—2006時間序列數據，使用偏移—份額法，從勞動生產率中分離出靜態結構變遷效應、動態變遷效應以及生產率增長效應。結果發現，經濟結構變遷對勞動生產率和經濟增長具有明顯的正向推動作用，但是隨著市場化程度的不斷加深，推動作用在減弱，“結構紅利”呈現出衰減態勢。［8］

（四）經濟波動與結構變遷交互作用實證研究

經濟波動作為總量增長率變動的直接表現，它與經濟結構變遷的交互作用在實證研究層面引起了學界的廣泛興趣。Burns認為在工業化過程中的不同時期，勞動力結構重心的轉變會對經濟波動產生不同的影響。起初，勞動力由政府部門、公共事業部門等就業穩定部門流向采礦業、建筑業、制造業、運輸業等不穩定部門，會加劇經濟波動。當勞動力由工農業部門流向服務業部門時，產業結構變遷對經濟波動的正向沖擊作用會減弱。［9］Warnock在Burns的研究基礎上，選取美國1946—1996年月度就業數據，運用隨機波動模型分析總體行業、三類生產性行業、六類服務業③的就業結構與波動特征，發現就業結構重心由不穩定（波動大）行業轉向穩定（波動小）行業時，會削弱總體經濟波動，這與Burns研究結果相悖。［10］Warnock認為，這種結果出現的原因是，制造業本身就業結構波動率的下降一定程度熨平了美國經濟波動，對美國經濟進入20世紀80年代的“大緩和”時期起到正向推動作用。Eggers選取1947—2001年10個經濟部門的產出數據，以穩定部門規模增加的1982年為時間節點將樣本分為兩期，把兩期產出變動歸因為結構效應、波動率效應、結構與波動率交互效應，結果表明，結構變動對經濟波動率的貢獻超過50%。［11］

在中國，產業結構變遷與經濟波動交互作用也一直廣受學界關注。馬建堂認為投資波動引發中國經濟波動，并進而驅動中國產業結構變遷。［12］他通過研究1952—1989年中國經濟周期波動過程中產業結構的變遷特征，發現工業波動與整體經濟波動具有一致性，農業波動方向與經濟波動方向相反，服務業由于受政治體制影響并未與整體經濟波動表現出明顯關聯特征。孫廣生的研究可以看作是馬建堂研究的延續與拓展。他將經濟部門細分至22個，在部門增加值指標基礎上加入投資指標，分析1985—2003年間中國各產業與整體經濟波動的相關性。結果發現工業與整體經濟波動相關性最強，其次是服務業，而農業并未與整體經濟波動表現出明顯相關性。進一步考察發現，重工業是經濟波動的主要推動者。［13］李猛認為，產業結構變動對中國經濟的沖擊引起了宏觀經濟周期性波動。［14］他采用實際份額法，測算出1952—2008年間，中國經濟周期波動中15%—20%的部分來源于產業結構不同程度的正向或負向沖擊。干春暉等將產業結構變遷分為產業高級化和產業合理化兩個維度，利用1978—2009年中國30個省（市）的面板數據，建立線性計量模型研究產業變遷對經濟波動的單向沖擊作用。結果表明，產業結構合理化對經濟波動具有抑制作用，而產業高級化則是經濟波動的主要來源。［7］

現代經濟增長過程中，總量變化與結構變遷相伴相生。改革開放以來，中國經濟增長與波動過程中伴隨著經濟結構演化。學界對經濟增長與結構變遷交互關系的研究，在研究方法上經歷了經驗性分析、描述性統計分析、現代計量手段的應用，研究指標的精細化、研究工具的現代化成為研究經濟波動與結構變遷交互關系的趨勢。但對相關文獻梳理發現，已有研究還存在兩點有待改進的地方：第一，刻畫產業結構變遷指標是與經濟增長是割裂的，無法搭建出二者交互的理論橋梁，僅憑借計量模型的改進，而無堅實的理論機制和理論模型，無法形成完整統一的分析框架；第二，對產業結構變遷與經濟增長交互關系的定量研究，往往是靜態的，或者是模糊掉時點的一種狹義動態關系，未能準確測算二者在各個時點的相關關系的數量特征。因此，本文在中國經濟部門非均衡增長直接導致經濟結構變遷的前提下，構建經濟總量增長速度的部門離散系數，作為經濟結構變遷系數，從而將經濟結構變遷與總量增長率變化有機聯系起來，直接考察其相關關系。為定量研究其相關關系的數量特征，建立非時變線性方程考察二者靜態總體相關性。考慮到改革開放以來，中國經濟發展的階段特征，二者的相關關系存在突變可能，進一步采用時變參數的狀態空間方程考察二者在經濟發展過程中各個時點的相關關系特征。

三、理論模型與研究假說

現代經濟增長的過程，不僅有總量的變化，也伴隨結構的演進。中國改革開放至今，經濟的高速增長伴隨經濟結構的高速變遷，是中國經濟最顯著的特征之一。經濟部門的非均衡增長直接導致產業結構的變遷，總量的高速增長則給予結構變化更高的彈性，結構高速演進的過程伴隨結構高級化和結構合理化，釋放出“結構紅利”推動經濟的高速發展。然而，總量增長率變化與經濟結構變遷交互作用的機理是什么呢？本文認為，二者交互作用的橋梁是技術進步。在技術進步的視角下，經濟的高增長率與結構的高變動率處在協同變化之中。

20世紀40年代至今，現代經濟增長理論出現了三次研究興趣的浪潮。其中，由索羅—斯旺新古典模型和受羅默—盧卡斯啟發的內生增長理論分別掀起了現代經濟增長理論的第二次、第三次浪潮，都將技術進步作為經濟增長的重要推動力量。在發展經濟學視角下，技術進步、體制變革和結構變遷構成了經濟發展的三維立體框架，經濟結構的演變則存在于技術進步與體制變革的交互作用之中。［15］技術進步視角下的總量增長與結構分化處在協同演化之中。首先，技術進步在部門間的應用路徑是由中心部門向外圍擴散、由少數行業向其他行業擴散，由此產生部門間勞動生產率差異分布，導致部門非均衡增長；其次，不同國家技術進步的水平差異，造成國家間經濟增長率分化，從而導致國際貿易中各國比較優勢的變動，引發國內生產結構的改變；技術進步對經濟的巨大推動作用，極大地改變社會發展面貌和人均收入水平，人們的消費需求也隨著收入水平的提高，逐漸從“必需品”轉移到“高檔品”和“奢侈品”，需求結構的轉變也必然直接帶動生產結構的轉變。

綜上，技術進步視域下經濟部門間的非均衡增長是結構分化的直接動因。在此基礎上，構建中國總體經濟增長速度的部門離散系數，作為中國經濟結構變遷系數，從而將經濟增長與結構演變有機聯系起來，直觀反映中國經濟增長與結構演變過程。參考鄭超愚［16］，中國經濟結構變遷系數構建過程如下：

假設中國國內生產總值Y按速度g經歷時間△T從Y0增長至Y1：

而經濟部門i國內生產總值Yi按速度gi經歷時間△T從增長至

從配第—克拉克定理到錢納里的“標準結構”，都表明在不同的經濟發展水平下都有相對應的經濟結構。因此，這里假設國民經濟部門結構由同期經濟總量決定。對應于初始國內生產總值Y0，初始國民經濟部門結構對應于目標國內生產總值Y1，目標國民經濟部門結構其中：

聯立以上四式，可得：

經濟結構變遷的基礎是國民經濟部門的非均衡增長，其經濟學層面的具體含義是國民經濟各部門總收入增速對國內生產總值增長速度的偏離。建立度量各部門國民收入增速gi對國內生產總值增速g的偏離程度的離散系數X，作為經濟結構變遷系數，以衡量國民經濟部門結構變遷：

聯立（5）式和（6）式，得：

進而：

這表明總量增長速度和經濟結構變遷系數存在正相關關系，理論上證實中國經濟增長與經濟結構變遷正向替換關系：當經濟擴張開始時，經濟結構變遷加快；當經濟轉入收縮階段時，經濟經濟結構變遷也開始變緩。

假定總量增長速度與經濟結構變遷系數存在穩定正比例關系，則有：

考慮到1978年以來中國經濟發展實際是向市場化、國際化、工業化以及城市化過渡的四重協同轉型過程，具有顯著階段特征。因此，假定總量增長速度與經濟結構變遷之間的比例系數具有時變特征，可得：

k(t)為非負時變函數，為確定經濟增長與經濟結構變遷之間的相關關系是穩定正比例的關系還是具有時變特征，下文將分別建立非時變線性方程和具有時變參數的狀態空間方程進行研究。

四、計量模型、方法和數據

（一）計量模型構建和方法說明

本文旨在從靜態和動態兩個視角考查經濟增長與經濟結構變遷之間替換關系的數量特征。文章選取1978—2016年的時間序列數據分別建立非時變參數線性模型和時變參數的狀態空間模型來研究這一問題。

從靜態視角構建非時變參數線性模型如下：

其中，gt表示經濟增長，Xt表示經濟結構變遷，μt為隨機擾動項。對該基本靜態線性模型，可以直接通過最小二乘估計（OLS）方法求解出參數β的最小無偏估計量。

如果考慮到表征經濟增長gt與經濟結構變遷Xt數量關系的系數β具有時變特征，即方程（12）結構有發生突變的可能，這時有必要借助鄒檢驗④（Chow test）發現方程（12）的結構突變時點，作為證實系數β具有時變特征的依據。一旦證實方程（12）存在結構突變點，這里有必要采用時變參數的狀態空間模型來定量研究經濟增長與經濟結構變遷之間的時變關系特征，模型構建如下：

式（13）被稱作量測方程，與方程（12）不同，這里βt是時變參數，反映了gt和Xt的時變關系。為描述出βt的時變軌跡，假定βt是符合一階馬爾科夫（Markov）過程：

假定ξt和γt無關，式（14）被稱作狀態方程。上述線性方程顯然是無法通過傳統的OLS估計方法求解，需設定初始狀態量條件E（β0）=α，借助于卡爾曼（Kalman）濾波算法進行求解。卡爾曼濾波算法是在量測方程和狀態方程擾動項ξt和γt、初始狀態量β0都符合正態分布的基礎上，通過已知信息量gt和Xt，對狀態量βt進行遞推式逐期最優估計，并且在求解過程中根據已知信息的逐步獲得，進行連續修正。

（二）變量與數據說明

對于經濟增長變量，本文選取中國1979—2016年實際GDP增長率作為衡量指標，年度實際GDP數據通過GDP平減指數化為1978年不變價格。數據來源于中華人民共和國國家統計局年度數據庫（http://www.stats.gov.cn/）。

對于經濟結構變遷變量，本文選取上文構建的經濟結構變遷系數X作為衡量指標。其中，經濟部門i表示農林牧漁業、工業、建筑業、批發和零售業、交通運輸、倉儲和郵政業、住宿和餐飲業、金融業、房地產業以及其他行業九個部門，九個部門1978—2016年增加值數據均來源于國家統計局年度數據庫，均經過對應分行業GDP平減指數化為1978年不變價格。

值得注意的是，現有主要直接衡量經濟結構變遷的指標有傳統產業結構變動值指標、Moore結構變化值、產業結構熵數以及產業結構超前系數等。鑒于在最近四十年經濟高速發展進程中，隨著市場化的不斷推進，經濟結構優化升級快速推進，中國經濟結構的變遷表現為產業結構高級化與產業結構合理化的協同推進。因此，近年來學者多從產業結構高級化與產業結構合理化兩個維度來衡量經濟結構變遷。為說明本文所構建的經濟變遷系數的合意性，這里對產業結構高級化指標、產業結構合理化指標以及筆者所構建的經濟結構變遷系數進行對比分析⑤。

如圖3，以SD、SA、SH以及X為指標描繪了1978—2016年中國經濟結構變遷情況。總體來看，本文構建的產業變遷系數X和經濟增長的變動情況較為一致，符合本文“總量增長速度和經濟結構變遷系數存在正相關關系”的假定。從表1來看，在三個時間段內，經濟變遷系數X和實際經濟增長率g相關性最高，且是正向相關關系。因此，從本文所要考察的經濟增長與經濟結構變遷之間相關關系的層面考慮，經濟變遷系數X是更合意的經濟結構變遷指標。進一步，從各指標內涵來看，SD是反映產業結構合理化的常用指標，表示經濟部門發展過程中對均衡狀態的偏離；SA和SH都是產業結構高級化的表征指標，前者是以第三產業與第二產業的產值之比計算得出，反映的是經濟發展過程中“經濟服務化”的傾向和水平。后者則是在部門份額比例變化的基礎上，引入勞動生產率要素，將產業結構高級演進過程從部門份額和勞動生產率兩個維度上進行衡量，避免產業結構的“虛高度”。產業結構高級化和合理化是產業結構演進趨勢的客觀要求，二者構成了產業結構調整與優化的基本目標。但僅僅從產業結構高級化與合理化兩個方面考慮經濟結構變遷是不客觀、不全面的，因此將SD、SA、SH單一或組合使用也是無法準確做到量化中國經濟結構變遷的。而本文所構建的經濟結構變遷系數X是在部門非均衡增長直接導致經濟結構變遷的基礎上直接構造，較為全面的描繪了中國經濟結構變遷過程。綜上，經濟結構變遷系數X是較為合意的指標。

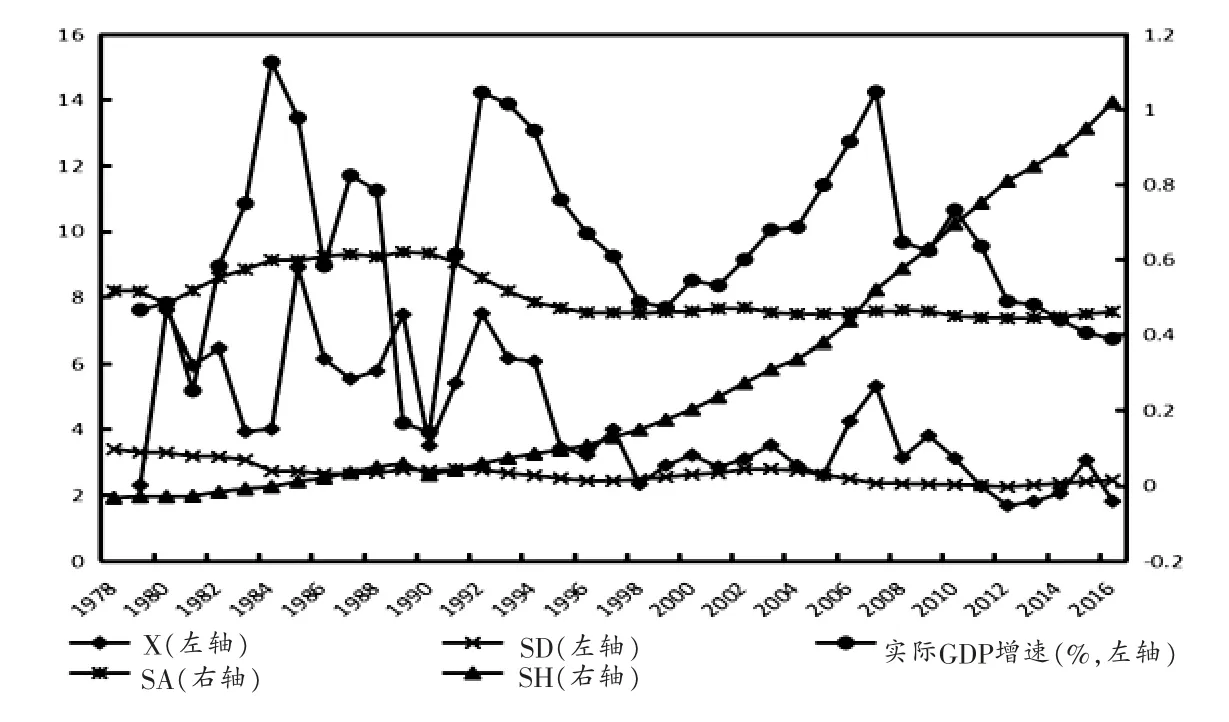
圖3 1978—2016年中國經濟結構變遷

表1 中國經濟增長速度與經濟結構變遷相關系數

五、實證分析

（一）中國經濟增長與經濟結構變遷存在協整關系

在運用相關計量模型對經濟增長與經濟結構變遷替代關系進行定量研究之前，必須要保證時間序列g和X是平穩的或者二者存在長期穩定的均衡關系。首先分別對時間序列g和X采用ADF檢驗（Augmented Dickey-Fuller test），通過觀察其是否存在單位根（Unit Root），來判斷其平穩性。表2所示，時間序列g和X均存在單位根，但其一階差分序列拒絕了存在單位根的假設，故二者均屬于一階單整I（1）序列。進而，有必要采用“E-G兩步法”對序列g和X線性組合的序列的平穩性進行考察。依上文式（12）構建關于序列g和X的線性方程并進行估算（結果見表3），然后運用ADF檢驗回歸方程殘差項的μt平穩性，如表2，序列μt在1%顯著性水平上拒絕存在單位根的假設，這表明經濟增長g與經濟結構變遷x之間存在長期穩定的協整關系。

表2 變量的平穩性檢驗

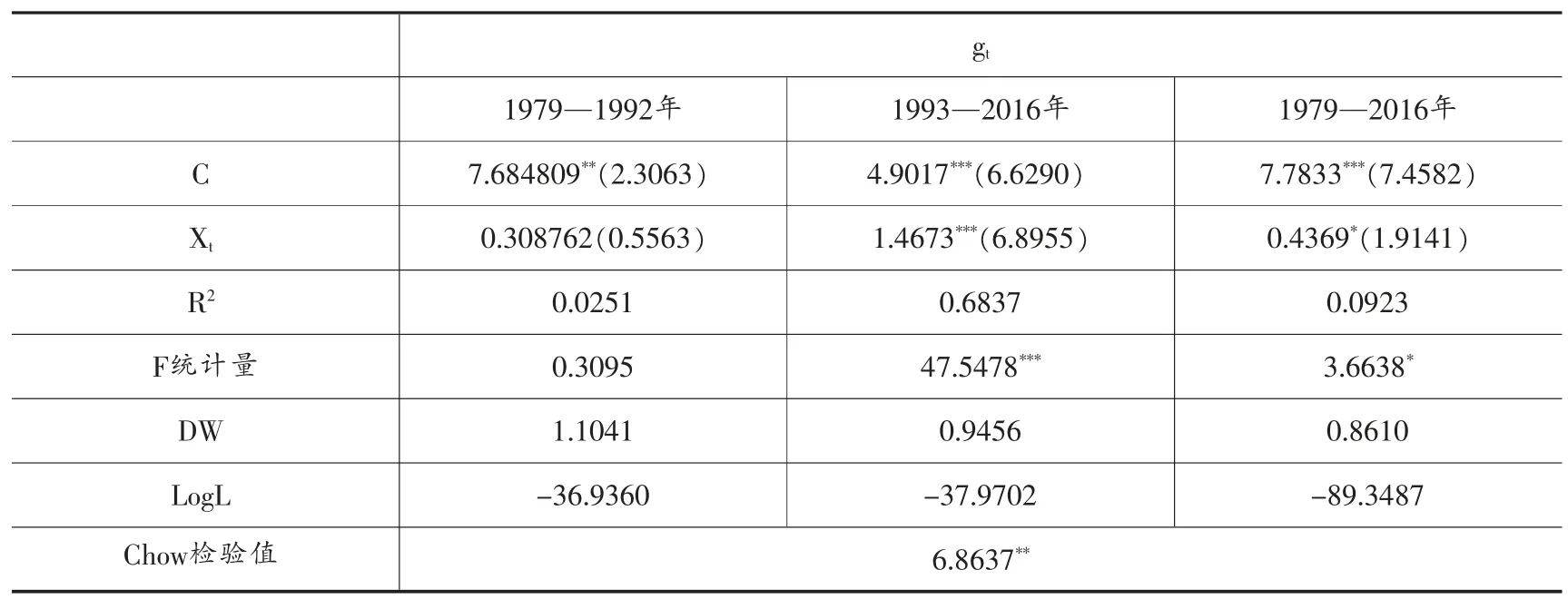
表3 中國經濟增長與結構變遷非時變參數方程估計結果

（二）中國經濟增長與結構變遷相關關系具有突變特征

在中國經濟增長與經濟結構變遷存在協整關系的基礎上，本文依照上文式（12）建立關于經濟增長和結構變遷系數的線性非時變方程，并采用OLS估計方法對方程參數進行估計，如表3所示：1979—2016年，經濟增長和結構變遷系數的彈性系數為0.4369，即經濟結構變遷系數每增加1個百分點，經濟增長上升0.4369個百分點；或者說經濟增長每提高1個百分點，經濟結構變遷系數增加2.2889個百分點。從當前結果來看，經濟增長與結構變遷存在明顯的相關關系。但考慮到改革開放以來，中國經濟發展實際是向市場化、國際化、工業化以及城市化過渡的四重協同轉型過程。其間，中國體制機制變革、經濟結構轉化以及科技進步都具有鮮明的階段特征，因此考慮表征經濟增長與結構變遷關聯特征的方程存在結構突變可能。利用Chow分割點檢驗，將方程結構突變點設置為1992年⑥。如表3，Chow檢驗值為6.8637，在5%的顯著性水平上拒絕方程在1992年前后無結構突變的假設。此外，比較1979—1992年和1993—2016年兩個時間區間的回歸方程估計結果發現，1993—2016年的回歸結果更加“理想”：參數顯著性、擬合優度R2、F統計量、對數似然函數值LogL更加合意，經濟增長與結構變遷的線性關系更顯著，這也在一定程度上說明，隨著時間推移，中國經濟增長與結構變遷的相關關系出現時變特征。綜上，中國經濟增長與經濟結構變遷存在明顯的正向相關特征，但是這種數量關系是不穩定的，具有某種時變特征。

（三）中國經濟增長與經濟結構變遷的時變關系特征

上文已證實中國經濟增長與經濟結構變遷之間存在的相關關系具有時變特征，本文進一步采用時變參數的狀態空間方程來考察這種時變特征，結果如式（15）（小括號內為t值）。

時變參數βt表征中國經濟增長與結構變遷之間彈性系數的變動趨勢，結果如圖4，以1997年為界，將樣本分為兩個時間區間。在這兩個時間區間內，βt呈現出不同的時變特征：1979—1997年間，βt波動幅度為0.55，而1998—2016年間波動幅度顯著降至0.08，這意味著中國經濟增長與結構變遷之間的彈性系數隨著時間推移出現波動緩和化趨勢；1979—1997年間，βt的平均值為0.20，即經濟結構變遷系數平均每增加1個百分點，經濟增長速度相應增加0.2個百分點，而1998—2016年間βt的平均值顯著升至0.42，這表明中國經濟增長與結構變遷之間的正向相關特征隨著時間推移呈現出明顯增強趨勢。

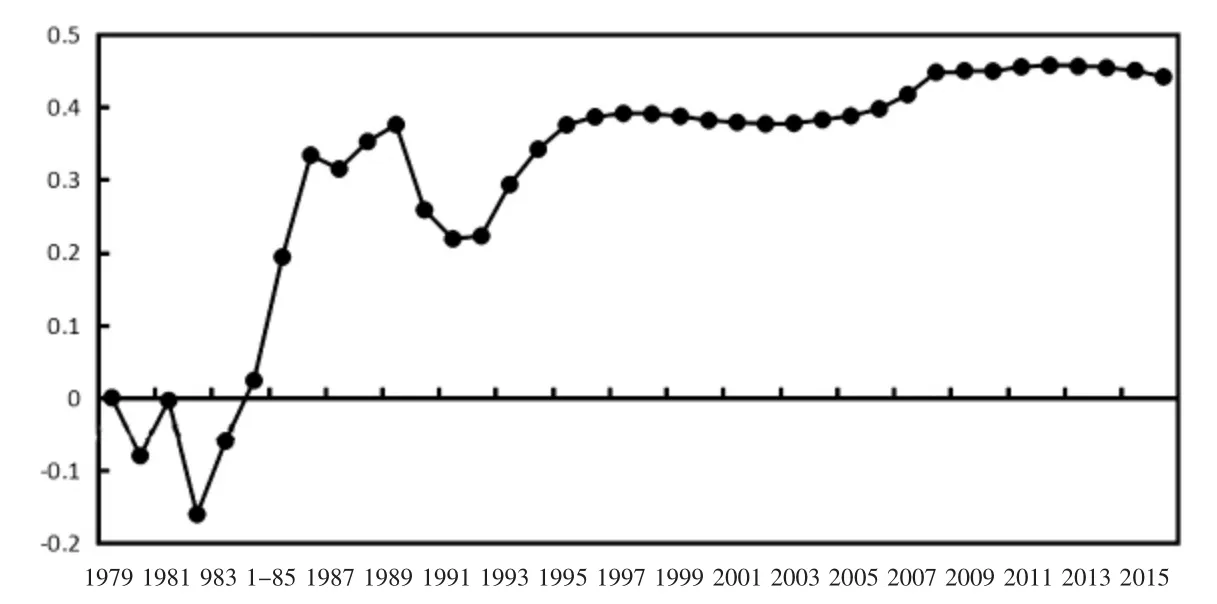
圖4 中國經濟增長與經濟結構變遷時變關系特征

綜上，1979—2016年間，隨著中國經濟發展進程的不斷推進，中國經濟增長與經濟結構變遷之間的相關關系出現了波動緩和化和彈性增強兩個方面的變化。中國社會主義市場經濟體制的建立與不斷完善或許是產生這種變化的關鍵因素。1992年黨的十四大正式提出建立社會主義市場經濟體制的目標，1997年十五大指出，當前財政、價格、金融、住房等體制改革得到大步推進，政府宏觀調控體系的框架已經初步建立，市場在資源配置中的基礎性作用顯著提高。1997年以后，中國經濟體制由計劃經濟體制主導轉向市場經濟主導，作為外部沖擊的政府宏觀調控體系不斷發展和完善，同時市場取代政府在資源配置中的基礎性地位。價格機制、競爭機制、產權制度、要素市場的建立與完善，為經濟發展注入強大生機與活力，是維持經濟增長與結構變遷高位平穩化的基礎性條件。1979—1997年，中國經濟增長與經濟結構都處在較大波動之中，其相關關系也出現高波動性，可稱之為二者相關關系的成長期；1998—2016年，中國經濟增長與經濟結構都出現波動緩和化趨勢，其相關關系也處于高彈性、低波動狀態，可稱之為二者相關關系的成熟期。

六、結論及政策啟示

1978年以來，經濟高增長和經濟結構高變動作為中國經濟發展過程中的兩大基本特征，二者相伴相生，深刻改變了中國經濟社會面貌。每輪經濟周期，中國經濟總量的擴張與收縮均伴隨經濟結構演化的加速與放緩。聯想到菲利普斯曲線中的經濟增長率和通貨膨脹率之間的替換關系，構建經濟總量增長速度的部門離散系數，作為經濟結構變遷系數，將中國經濟增長與結構變遷有機聯系起來，并通過理論模型推導出中國經濟增長與結構變遷之間存在正向關系的命題。分別建立非時變線性方程和時變參數的狀態空間方程分析經濟增長與結構變遷相關關系的靜態和時變特征。本文主要結論有：第一，1979—2016年，中國經濟增長與經濟結構變遷總體呈現出顯著的正向關系；第二，中國經濟增長與結構變遷之間相關關系具有顯著時變特征，1979—1996年，中國經濟增長與經濟結構都處在較大波動之中，其相關關系處于高波動的成長期。1998—2016年，中國經濟增長與經濟結構均表現出波動緩和化趨勢，其相關關系也處于高彈性、低波動的成熟期。

結合本文研究結論，提出如下建議：

第一，經濟持續下行背景下，經濟結構調整政策應更加“有為”。中國經濟增長與經濟結構調整之間的正向關系已進入高彈性、低波動的成熟期。經濟新常態下，經濟總量增速放緩，經濟結構變遷進程也隨之放緩，部門經濟增長趨于平衡化。在實施產業結構調整政策時，若以結構調整帶來的潛在收益（經濟部門增速趨同）來平衡經濟總量增速下滑的現實成本，勢必影響產業高級演進過程。完全依靠市場的力量實現出清以擺脫經濟低迷狀態是不現實的，即便市場出清后，失業率攀升、產出偏離長期均衡也會成為大概率事件，并不會出現理想市場條件下的結構優化。因此，更加“有為”的經濟結構調整政策是克服經濟發展、結構轉型過程中出現的市場失靈和體制機制缺陷的“良藥”，有利于經濟的平穩健康發展和經濟結構的高級演進。

第二，努力恢復經濟增長的樂觀態勢，為結構調整創造必要條件。中國經濟結構調整是在經濟總量持續快速增長背景下完成的，經濟總量的高位平穩化增長為結構調整創造了較大的彈性空間和基礎條件。經濟結構漸進有序調整不可能在經濟蕭條或過熱的極端條件下進行。當前中國經濟處于持續下行區間，海外市場萎縮明顯、國內市場需求不足無法為結構調整創造良好的條件，加之相應價格信號失衡無法為結構調整指示合理的方向。因此，政府應當實施更加積極的財政政策和貨幣政策，努力恢復中國經濟增長的樂觀態勢，推動經濟結構的高級演化進程。

第三，健全技術創新機制，推動經濟增長與結構調整。中國經濟增長經歷了粗放式向集約式的轉變，伴隨著中國經濟結構向現代經濟結構的不斷深化。這其中最重要的動力之一就是科技創新，在技術進步力量的推動下，經濟總量增長與結構分化處在協同演化之中。在世界現代經濟發展進程和中國特色社會主義經濟的實踐中，科技創新的巨大推動力量成為社會共識并得到高度重視。為實現經濟持續高位平穩發展、經濟結構高級化進程快速推進，仍需完善創新人才評價體制，提升國家創新體系整體效能；健全現行科技創新法律法規體系，形成規范且操作性強的法規體系；加強國家層面重大科技攻關計劃，尋求關鍵核心技術的更大突破。

注釋：

①經濟變遷系數是本文在中國經濟部門非均衡增長直接導致經濟結構變遷的前提下，構建的經濟總量增長速度的部門離散系數，用來衡量經濟結構變遷程度，在文章第三部分會詳細介紹構建過程。

②兩個目標不可兼得，呈現置換關系(trade off)。

③三類生產性行業：采礦業、建筑業、制造業；六類服務業：狹義服務業、政府部門、公共事業部門、批發業、零售業、金融保險及房地產業。

④鄒檢驗：通過選定一個時間點，將樣本分為兩個子樣本區間，利用OLS估計方法對總體樣本和兩個子樣本進行回歸，得出總體樣本殘差和子樣本殘差。通過構建F統計量比較總體樣本殘差與子樣本殘差，判斷在時間點上方程是否發生結構性變化。如果F統計量超過臨界值，則認為該方程在選定的時間點上發生結構突變，此時，該時間點被稱作間斷點。

⑤這里選用產業結構偏離度（SD）作為產業結構合理化衡量指標，具體構建過程詳見干春暉等［9］；分別選用第三產業產值與第二產業產值之比（SA）、產業結構高度（SH）作為產業結構高級化衡量指標，具體構建過程詳見干春暉等、劉偉等［7］［8］。

⑥參考鄭超愚觀點，1978—1991年是中國計劃經濟主導期，1992年以后是中國市場經濟主導期，經濟增長與結構變遷的相關性會在兩個時期表現出不同的特征［18］。本文表1也顯示，在1992年以后，經濟增長與結構變遷的相關性比1992年以前顯著提高，故本文將方程結構的突變點選為1992年。