基于油水相指數時變的相對滲透率計算方法
翟上奇 雷 源 孫廣義 張言輝 常會江
中海石油(中國)有限公司天津分公司渤海石油研究院, 天津 300459
0 前言
相對滲透率曲線是研究儲層巖石兩相滲流的基礎[1-4],是油田數值模擬及動態分析不可缺少的重要資料。目前國內外對于相對滲透率的研究主要集中在相對滲透率數據的處理以及相對滲透率規律的應用,對于數據獲取方法的研究相對較少,且大部分研究以稠油為主[5-10]。目前獲取相對滲透率數據主要是通過非穩態法實驗方法[11-14],這種方法操作簡便、用時較短,具有普遍適用性,但非穩態實驗中油水計量點往往從油水同出點后開始,使得數據點在中高含水飽和度處較為集中,不能完整地反應整個開發歷程。
渤南區域油田,主力油層黏度基本在0.35~34.9 mPa·s,7成比例油田黏度甚至小于10 mPa·s,密度0.831~0.928 g/cm3,形成了屬中輕質黏度范疇的油田群。在其他物性條件及開發方式相近的情況下,水油黏度比越高,分流率曲線的凹形就越強,該類油田相對稠油油田具有較長的無水采油期或低含水期。在應用非穩態法獲取相對滲透率曲線時發現,水驅前緣數據點較少易造成研究人員對初期開發規律認識不清,數值模擬歷史擬合誤差較大,這些因素都嚴重制約了相對滲透率曲線的應用。
文章以渤南區域A油田為例,利用廣適水驅曲線進行中低含水期含水飽和度計算,并將傳統相對滲透率計算模型進行改進,創新性地提出基于油水相指數時變的相對滲透率計算方法,實現低含水期相對滲透率數據加密。
1 中低含水期含水飽和度Sw計算
(1)
式中:R為采出程度,%;Sw為含水飽和度;Swi為束縛水飽和度。
由式(1)可知,已知不同時刻的采出程度可以計算相應的含水飽和度Sw。對于人工水驅開發的油藏,水驅曲線法可以很好地表達不同時刻采出程度與含水率的關系[15-17]。我國石油天然氣行業標準推薦使用甲型、乙型、丙型、丁型等4種水驅曲線,不同的水驅曲線對于地層原油黏度有不同的適應條件,含水上升規律不盡相同。其中,甲型、丙型適用于地層原油黏度3~30 mPa·s的中等黏度油田,乙型適用于地層原油黏度大于 30 mPa·s 黏度較大的油田,丁型水驅曲線適用于黏度較小的稀油油田。但是甲、乙、丙、丁四種水驅曲線的適用條件均為含水率達到50%以上的油田,增加了中低含水期數據獲取的困難。
針對這一問題,本文采用廣適水驅曲線對該油田數據進行處理,研究表明,廣適水驅曲線可以表征各類型含水上升規律,對于油田的非均質性有更強的適應性,最重要的是,廣適水驅曲線在中低含水階段就會出現直線段,出現的時機要遠早于甲型、丙型的直線段出現時機,因此采用該方法計算中低含水期含水飽和度更為準確可靠。
廣適水驅曲線的表達式為:
(2)
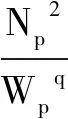

由式(2)可得:
(3)
(4)
式中:fw為含水率。
由式(1)可知,
(5)
將式(5)帶入式(4):
(6)
由巖心實驗獲取的相滲曲線可知束縛水飽和度Swi,已知油田地質儲量N,技術可采儲量NR、累產油量Np,待定常數q、a,不同時刻的含水飽和度Sw可根據式(6)計算。

圖1 廣適水驅曲線線性擬合程度圖
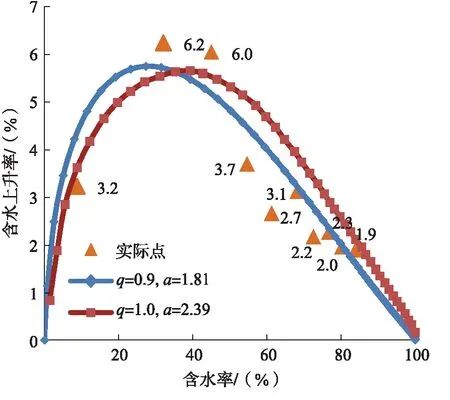
圖2 廣適水驅曲線含水上升率與含水率關系圖
2 油水相對滲透率計算
據筆者調研,近年來常用的相對滲透率計算模型見表1。由表1可看出,不同的模型表達方式多樣,但Kro與Krw基本與含水飽和度Sw成冪函數關系,經過調研及實際論
證[18-20],其中Willhite方程可靠性更高,表1中,Swi為束縛水飽和度;Sor為殘余油飽和度;m、n分別為油、水相指數;Krw為水相相對滲透率;Kro為油相相對滲透率;So為含油飽和度;?為孔隙度;Kw(Sor)為殘余油下水相滲透率,10-3μm2;Ko(Swi)為束縛水下油相滲透率,10-3μm2。
表1 常用的油水相對滲透率模型

提出者提出時間相對滲透率計算模型Pirson1958Kro=(1-Sw)2;Krw=(Sw-Swi)2(1-Swi)2Sw4Brooks-corey1966Kro=(1-Sw)2[1-Sw(2+a)/a];Krw=Sw(2+3a)/aHonarpour1982Kro=0.760 67So1-Swi-Sor1-Soré?êêêù?úúú1.8(1-Sw)2+2.631 8?(1-Sor)(So-Sor)Krw=(Sw-Swi)1.581 4(Sw-Swi)0.91(1-Swi)0.91-0.581 7(1-Sw)-1.248 4?(1-Swi)é?êêù?úú陳元千1984Kro=(1-Sw)3;Krw=Kw(Sor)Sw3Willhite1986Kro=Ko(Swi)(1-Sw)n;Krw=Kw(Sor)Swm李克文1989Kro=Ko(Swi)(1-Sw)n+a(1-Sw)1+aKrw=Kw(Sor)Swm+bSw1+b張繼成2007Kro=10aSw+b-Co;Krw=10cSw+d-Cw
由水油比的定義可知,
(7)
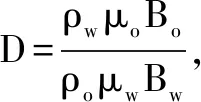
(8)
式中:ρw為地層水密度,g/cm3;ρo為地層原油密度,g/cm3;μo為地層原油黏度,mPa·s;μw為地層水黏度,mPa·s;Bo為地層壓力下原油體積系數;Bw為地層水體積系數;WOR為水油比,無量綱;Qw為日產水量,m3;Qo為日產油量,m3。
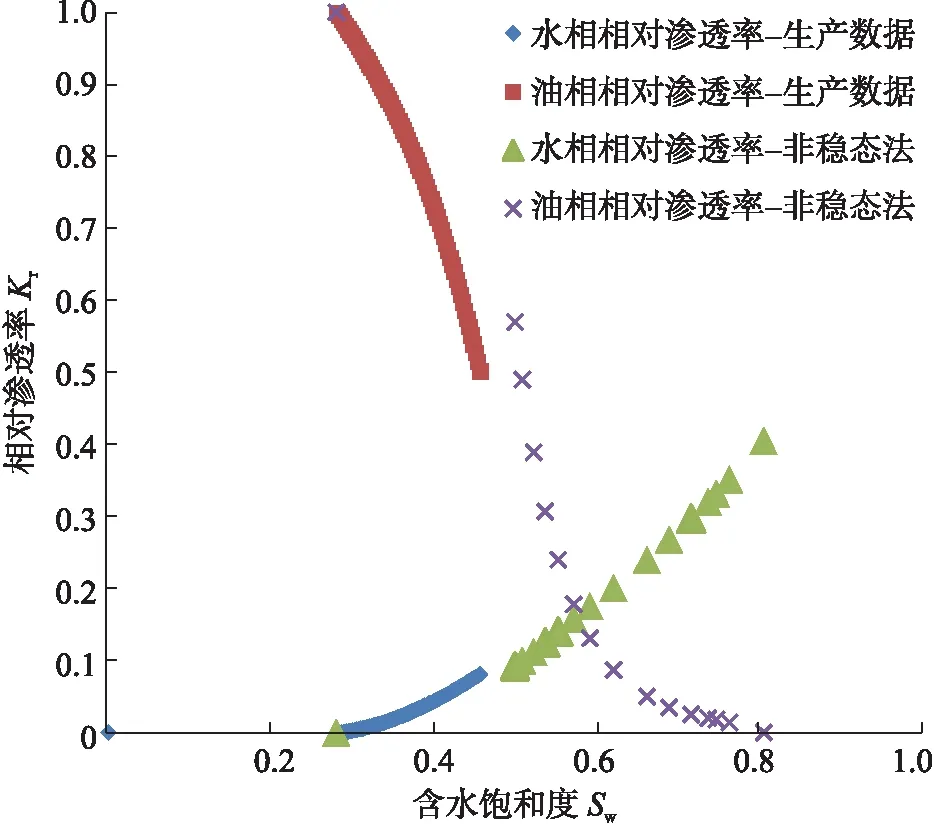
圖3 A油田修正前油水相對滲透率曲線圖(生產數據計算vs非穩態法)
由圖3可以看出,模型計算結果與實驗數據吻合程度不高,油相、水相數據與實驗數據擬合均有偏差,尤其是含水飽和度越低,擬合油相數據點誤差越大。油、水相指數直接決定相對滲透率曲線的陡峭程度,因此,擬合效果較差與油水相指數有較大關系,這些現象表明,油相、水相指數并不是常數,可能與含水飽和度相關。由于Kro與Krw基本與含水飽和度Sw成冪函數關系,在本文中,假設m、n也與Sw成冪指數關系。將相對滲透率計算模型進行修正:
(9)
(10)
根據A油田實際參數對式(9)、(10)計算,得到各個參數如下:a=-1.30,b=2.87,c=0.005,d=-5.76,m=2.11,n=1.20。利用新模型進行計算,結果見圖4。由圖4可以看出,該模型與實驗數據吻合程度較高,假設可靠。
3 穩態實驗法驗證
相對滲透率實驗方法主要包括穩態法及非穩態法兩種,穩態法中流體飽和度可以直接測量計算,原理基于達西定律,但由于該方法耗時較長,操作不便,因此常采用非穩態法代替,非穩態法忽略毛管壓力及重力影響,為了消除末端效應要求高速驅替。為了驗證非穩態法及生產數據計算得到的相滲曲線是否合理,本文開展穩態法對其進行驗證,實驗結果見圖5。在一定條件下,三種方法相滲曲線形態較為一致,尤其是中低含水飽和度下符合程度更高,證明該計算方法能夠反映地下流體的滲流規律,對于中輕質油田中低含水期相滲數據的獲取具有推廣及指導意義。
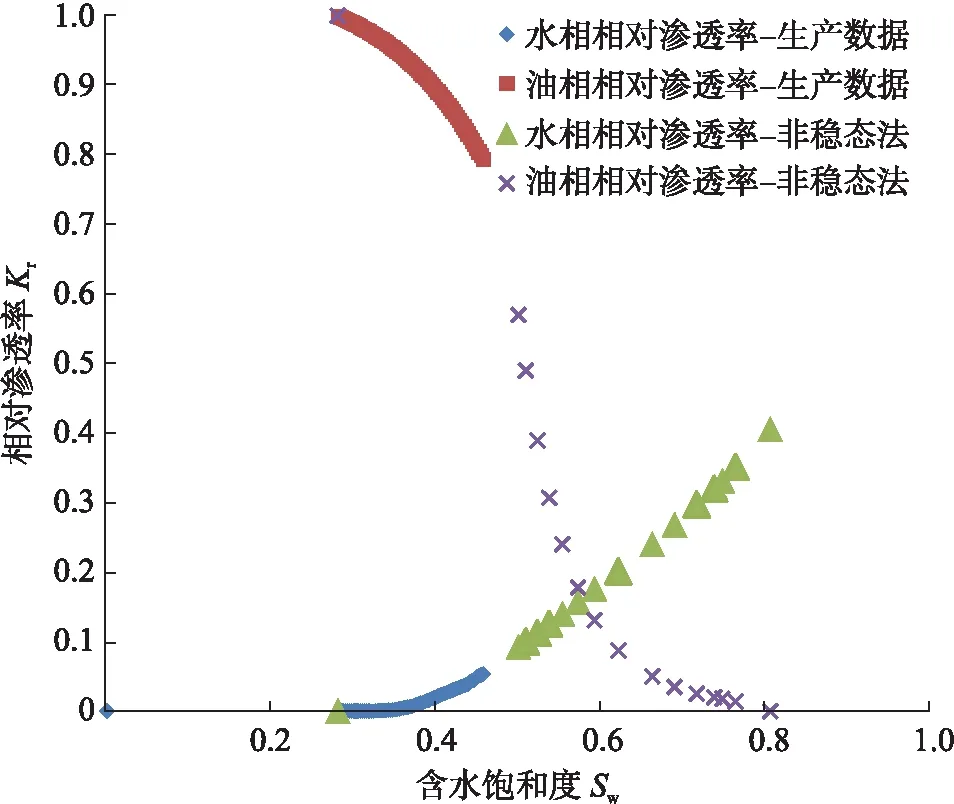
圖4 A油田修正后油水相對滲透率曲線圖(模型計算vs實驗)
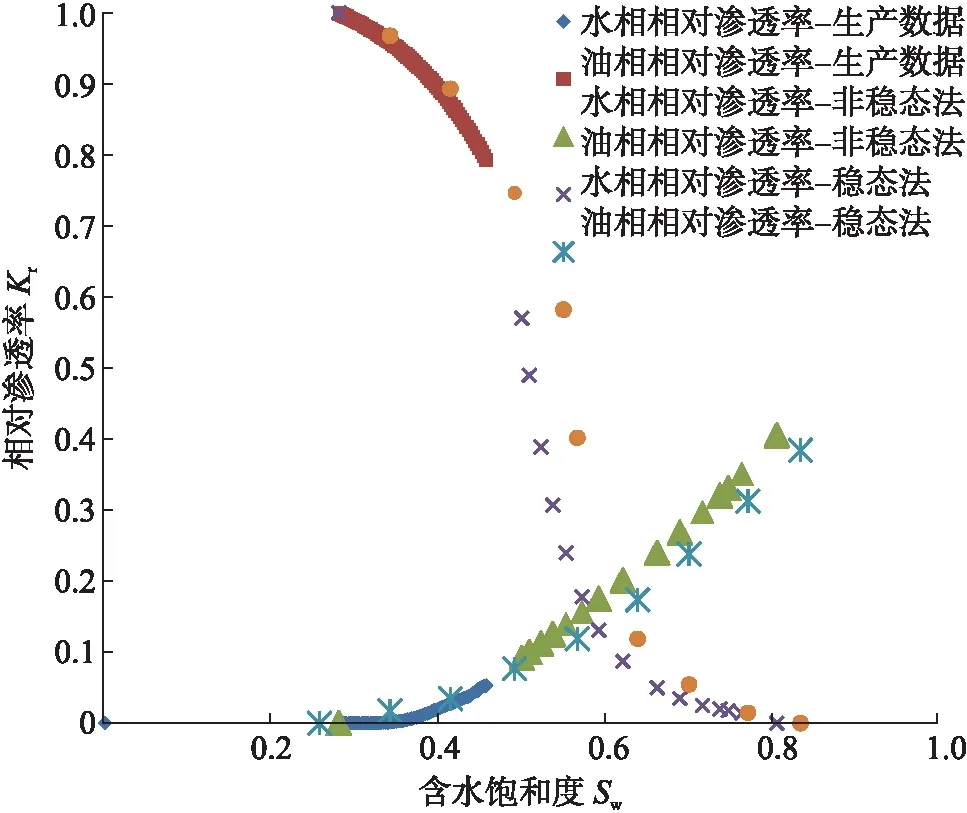
圖5 A油田油水相對滲透率曲線圖(生產數據計算vs非穩態法vs穩態法)
4 結論
本文以渤海A油田為例,針對非穩態實驗法測得的相滲數據不能準確反映中輕質油田早期的開發特征問題,采用廣適水驅曲線進行中低含水期含水飽和度計算,并將傳統相對滲透率計算模型進行改進,創新性地提出基于油水相指數時變的相對滲透率計算方法,實現低含水期相滲數據加密,得到如下結論:
1)對于中輕質油田,當非穩態實驗法不能獲取理想的低含水期相滲數據時,可以采用合理的相對滲透率模型進行計算,本文采用的計算模型相比其他模型精度更高。
2)廣適水驅曲線在中低含水階段就會出現直線段,對于中輕質油田低含水期數據的獲取推薦使用廣適水驅曲線。
3)油相與水相指數并非常數,是與含水飽和度有關的函數,考慮油水相指數時變后,相對滲透率曲線的計算更為準確。

