與“圓”有關的切線問題初探

鄭小華

摘 要：縱觀全國各地中考題，與“圓”有關的計算與證明是中考的必考內容之一，占有較大比重，通常結合三角形、四邊形等與圓有關的位置關系進行綜合考查，以計算題、證明題的形式出現，解答此類問題要熟練掌握圓的基本性質，特別是切線的性質和判定，同時要注意已知條件之間的相互聯系。文章對與“圓”有關的位置關系進行了相關探索。

關鍵詞：“圓”;切線;解題思路

筆者翻閱全國各地中考試卷發現，近五年來中考對“圓”的考查一般會出現在填空題第8題，或作為選擇題出現在第14題或第16題，廣東省中考卷中連續幾年將與“圓”有關的計算與證明題作為9分壓軸題之一放在解答題（三）中的第24題。

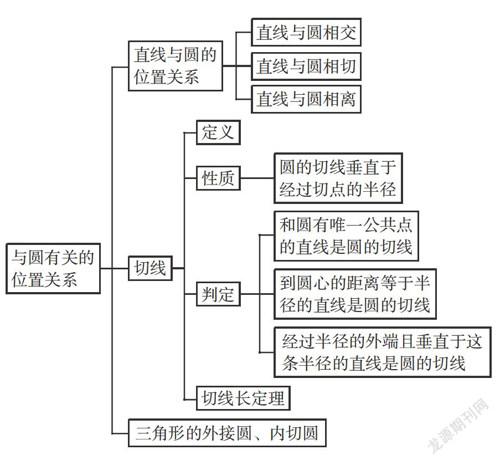
一、知識思維導圖

二、重點及難點問題解析

知識點一 直線和圓的位置關系的判定及性質

設⊙O的半徑為r，圓心O到直線l的距離為d，直線l和⊙O相交？圳dr。

（1）“？圳”號左邊是直線和圓的位置關系，右邊是圓心到直線的距離和半徑大小的數量關系;（2）直線和圓的位置關系和圓心到直線的距離與半徑的大小關系是一一對應的;（3）從左邊推出右邊是直線和圓心的位置關系的性質，從右邊推出左邊是直線和圓的位置關系的判定。

知識點二 切線的判定定理及性質定理

（1）在應用判定定理時注意：①切線的兩個條件：經過半徑外端;垂直于這條半徑。②切線的判定定理的出處：“圓心到直線的距離等于半徑時，直線和圓相切”。③在判定一條直線為圓的切線時，當已知條件中未明確指出直線和圓是否有公共點時，常過圓心作該直線的垂線段，證明該線段的長等于半徑，可簡單地說成“無交點，作垂線段，證半徑”;當已知線段中明確指出直線和圓有公共點時，常連接過該公共點的半徑，證明該半徑垂直于這條直線，可簡單地說成“有交點，作半徑，證垂直”。（2）在應用性質定理時應注意：①切線和圓只有一個公共點;②圓心到切線的距離等于半徑;③經過圓心并垂直于切線的直線必過切點;④經過切點并垂直于切線的直線必過圓心。

知識點三 切線長定理

（1）切線是一條直線，無法度量其長度;而切線長是切線上一條線段的長;（2）經過圓外一點，可以作兩條直線與該圓相切;（3）因為切線長是切線的一部分，所以切線的所有性質適合切線長;（4）切線長定理包含著垂直、全等、弧相等等關系，在一些證明求解問題中經常用到。

三、典型例題剖析

題型① 直線和圓的位置關系的判定及性質的應用

【例1】已知⊙O的圓心O到直線l上一點A的距離等于⊙O的半徑，試判斷直線l和圓O的位置關系。

解析：要判定直線l和⊙O的位置關系，必須先弄清⊙O的圓心O到直線l的距離與半徑的大小關系，此題有兩個可能：一是直線l與O相切;二是直線l和⊙O相交。

答案：相切或相交。

點撥：區分開OA的長度不一定是圓心O到直線l的距離。

【類題突破1】在△ABC中，∠C=90°，∠B=30°，O為AB邊上一點（不與點A重合），AO=m，⊙O的半徑r=，則m在什么范圍取值時，直線AC與⊙O相交？相切？相離？

答案：過點O作OD⊥AC于點D，

則∠AOD=∠B=30°。

∵OA=m，

∴AD=am，

∴OD=a=am

當ODr，直線AC與⊙O相離。

點撥：過圓心作垂線→計算的OD長→比較OD與r的大小關系→結論。

題型② 切線的判定定理與性質定理的應用

【例2】如右圖所示，已知△ABC中，AB=AC=13cm，BC=10cm，以AB為直徑作⊙O，交BC于D，交AC于E，過D作DF⊥AC于F。

求證：DF是⊙O的切線

解析：由題意知，DF與⊙O有公共點點D，

故只需證OD⊥DF即可。

答案：連接OD、AD，

∵AB是⊙O的直徑，

∴∠BDA=90°，∴AD⊥BC。

又∵AB=AC=13cm，BC=10cm，

∴BD=DC=aBC=5cm。

又∵AO=OB，∴OD∥AC。

又∵ DF⊥AC，∴ DF⊥OD。

即DF是⊙O的切線。

點撥：在切線的三種判定方法中，常用的有兩種：①當題目中未出現直線與圓的公共點時，一般過圓心作直線的垂線段，證明垂線段的長等于半徑;②當題目中出現了公共點時，往往連接該點與圓點，證明這條半徑與直線垂直即可。

【類題突破2】已知，直線l與⊙O相切于點C，AD為⊙O的直徑，點B在直線l上，且∠BAC=∠CAD（AB與AD不在同一條直線上），先畫出圖形，試判斷四邊形ABCO的形狀，并證明你的結論。

解析：在審題的過程中我們可以先根據題意畫出⊙O與它的切線l，再畫出直徑AD，最后根據∠BAC=∠CAD確定點B的位置，在探究四邊形ABCO的形狀時，可將直徑AD轉動，得到幾個不同的位置進行觀察和猜想，發現在一般情況下，四邊形ABCO是直角梯形，特殊到當AD∥l時，四邊形ABCO就變成了正方形，所以在我們在解題的過程中要分兩種情況進行討論。

答案：如圖（1），當AD與直線l不平行時，四邊形ABCO是直角梯形，證明如下：

∵在⊙O中，OC=OA，

∴∠ACO=∠CAD。

又∵∠BAC=∠CAD，

∴∠BAC=∠ACO，∴ AB∥OC。

∵⊙O與直線l相切于點C，

∴∠OCB=90°，

又∵AD與直線l不平行，

∴四邊形ABCO為直角梯形。

如圖（2），當AD與直線l平行時，四邊形ABCO是正方形，同（1）可證得BA∥OC，∠OCB=90°。

∵AD∥l，

∴四邊形ABCO為矩形。

又∵OA=OC，

∴四邊形ABCO為正方形。

方法規律：在解答有關判斷形狀的問題時，一般情況下先將圖形移動做適當的變化，然后從各種不同的位置進行觀察、猜想和論證。當因為圖形的變化而得到不同的情況時，要對產生的不同的情況分別進行討論。

題型③ 三角形的內切圓的考查

【例3】如圖，MA，MB是⊙O的兩條切線，A、B為切點，若∠AMB=60°，AB=1，則⊙O的直徑等于（?  ）。

A. a B. 2a

C. a D. a

解析：如圖，要求直徑，可考慮求半徑，由于MA、MB為切線，A、B為切點，∠AMB=60°，連接OA、OM，設OM交AB于C，易知OA⊥AM，

∠AMO=a∠AMB=30°，又OM⊥AB，所以∠OAB=∠AMO=30°，AC=aAB=a，所以OA=a。答案D。

【類題突破3】如圖，在圓I 中，AB=AC=5，BC=6，E、F分別是邊AC、AB與圓I的切點。求圓I的半徑。

答案：過點A作AD⊥BC于點D，則AD為∠BAC的平分線，則I在AD上。∵AB=AC=5，BC=6，∴AD=4。如圖，連接IE，則IE⊥AC，設I半徑為x。

∵∠IAE=∠CAD，∠AEI=∠ADC，

∴△AIE∽△ACD。

∴a=a，即a=a

解得：x=a，故△ABC的內切圓I的半徑為a。

規律總結：關于“圓心與切點”：①點心連（圓心與切點）是解決圓的問題中的最常用的輔助線。②若想要證明某條直線是圓的切線，若題目中沒有明確指出圓和直線是否有公共點，那么就首先想到經過圓心作這條直線的垂線段，再去證明這條線段的長等于這個圓半徑，這就是傳說中的“無交，垂也，證半徑”。③在證明直線與圓相切的過程中，如果題目中已知明確直線與圓有公共點，那么就可以用“點心連”連圓上的點和圓心，再去證明該條直線是否垂直于該條半徑，“作半徑，證垂直”。④當圓中已說明有直徑時，通常要想到構造圓周角，即“有直徑，造直角”。

關于“三角形與圓的關系”：①三角形的外心與內心都有許多固定的性質，如銳角三角形的外心在三角形內部，直角三角形的外心在斜邊中心，鈍角三角形的外心在三角形外部，等腰三角形的外心和內心在底邊的中線上，等邊三角形的內心和外心重合。②在三角形內切圓有關問題中，常用代數式方法解決幾何問題，一般解法是設未知數列方程。

遇到圓外三角形時注意切線長定理的應用，切線長定理包含著一些隱藏結論，如下圖：

①MA=MB，∠1=∠2;②直線MC是弦AB的對稱軸;③P為AB的中心，C為ACB的中心。

四、結語

總之，遇到與圓有關的位置關系問題，我們要做到切線“一看”“二算”“三證明”。“一看”，即看看題目中有沒有說到唯一的公共點;“二算”，即算算圓心到直線的距離是否與圓的半徑相等;“三證明”，即證明一經過，二垂直。

在求切線長的過程中，經常要與切線的“三理”（性質定理、勾股定理、垂徑定理）進行深度融合及綜合運用。熟練掌握三角形的內切圓和內心的相關概念。