對《倍數與因數概念》引入方式的思考

樓俊民

摘要：《倍數和因數的概念》在北師大版五年級上冊的第31-32頁，是第三單元《倍數與因數》的起始。它是在學生學過整數的認識，整數的四則運算等知識的基礎上展開學習的。同時，倍數與因數的概念也是以后學習質數和合數，公倍數和公因數等概念的重要基礎。對于以何種方式引入因數與倍數的概念，不同版本的教材有著不同的安排。

關鍵詞：倍數;因數;小學數學

一、現行各版本教材的安排

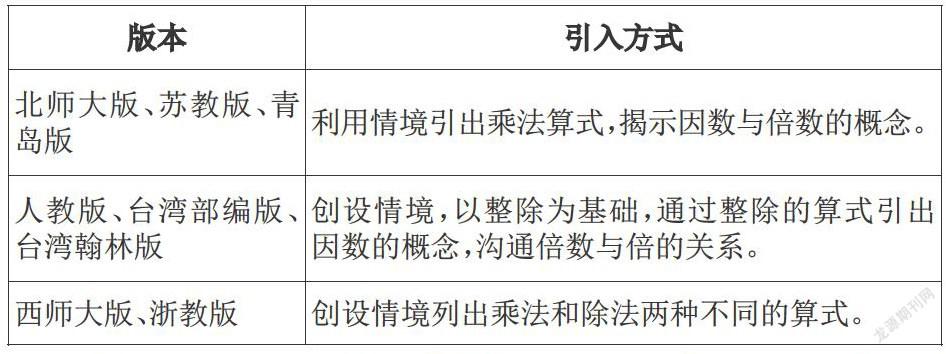
這里選取八套教材：人教版、北師大版、蘇教版、西南師大版、青島版、浙教版。對比分析后發現引入的材料可以分成三類：

從表中可以看出，各版本教材有從乘法算式引入的，有從除法算式引入的，也有折中考慮，同時列出乘法和除法算式來引出因數與倍數概念的。這一方面是由于乘除法之間的互逆關系，無論是乘法算式引入，還是除法算式引入，在本質上都是相通的。另一方面也說明專家對如何引出因數和倍數概念并不統一。不論是乘法算式引入，還是除法算式引入，都有不同的利和弊。在取舍時，出于不同的考量，所以做出不同的安排。

二、下面以北師大版和人教版作為典型對各自的利弊展開分析

（一）北師大版教材的安排

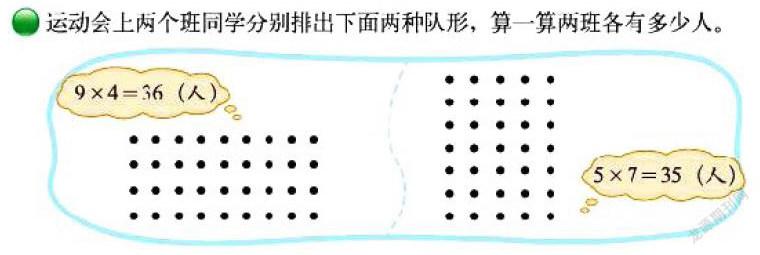
北師大版是這樣引入因數和倍數概念的。首先創設兩個班同學分別排列成兩種隊形，算一算兩班各有多少人的情境，讓學生根據情境寫出乘法算式。

接著，結合具體的乘法算式，給出倍數與因數的意義，也就是由9×4=36，可以判斷出36是9和4的倍數，9和4是36的因數。把乘數與積的關系轉化為倍數與因數的關系。同時，借智慧老人的告知學生“只在自然數（零除外）范圍內研究倍數和因數。”

然后，對給定的兩個算式，判斷倍數與因數，說一說哪個數是哪個數的倍數，哪個數是哪個數的因數。通過模仿練習，幫助學生正確區分倍數和因數，鞏固和掌握倍數與因數的概念。

可以看出，北師大版教材沒有從整除的概念出發，而是采用一個乘法算式直接引出“因數”和“倍數”的概念。相對于除法而言，乘法更容易為學生理解，因為用乘法算式，學生就不必通過a能被b整除，來反推出b是a的因數，a是b的倍數，從而大大降低了學生判斷因數和倍數的難度。教學用書中提到：“在內容安排上適當降低了知識難度……沒有出現整除、互質數、質因數、分解質因數等數學概念”這也能佐證采用乘法算式來揭示倍數與因數的概念，是出于降低難度的考慮。

但是從知識邏輯的角度來看，因數與倍數的概念是在整除的基礎上產生的。在整數除法里，如果整數a能被整數b（b≠0）整除，那么a叫作b的倍數，b叫作a的因數。也就是說，從邏輯上來講整除是產生因數與倍數概念的前提，有了整除，才有了因數和倍數;離開了整除，因數和倍數的概念就好比是空中樓閣，無從談起。所以，倍數與因數的概念，本身是與整數四則運算有著密切關系的。可以利用學生已有的整除的知識，構建出因數與倍數的概念。北師大版教材在揭示因數和倍數的概念后，借智慧老人以告知的形式規定“在非0自然數的范圍內研究倍數和因數”，這里總是讓人感到數學不夠講道理。

（二）人教版教材的安排

人教版教材由9個整數除法算式引入。首先通過觀察，對算式進行分類。在分類的基礎上，概括出其中一類具有“商是整數而沒有余數”的共同屬性。

然后，結合整除算式12÷2=6，給出因數和倍數的概念。如果12÷2=6，那么12是2和6的倍數，2和6是12的因數。這個過程，雖然沒有給出整除的定義，但是確實是由整除的本質過渡到因數和倍數的概念的。接著，回到第一類的除法算式中判斷倍數與因數，說一說誰是誰的倍數，誰是誰的因數。讓學生正確區分倍數和因數，同時體會倍數和因數相互依存的關系。

通過對比，可以看出人教版與北師大版的區別主要在引入材料上的不同。學生對整除是有豐富的經驗的，在前面整數四則運算的學習中，學生已經積累了大量的整除和有余除法的知識基礎和認知經驗，對整除的意義已經有了比較清楚的認識，判讀一個數能否被另一個數整除是不困難的，幾倍的概念也已經存在于學生的頭腦中。

對此，筆者傾向于通過喚醒學生原有的知識經驗來引入因數和倍數，因為這樣更符合學生的認知規律，更有利于因數與倍數概念的建立。有根源的知識，才會生根發芽，成為學生自主建構體系的一部分

參考文獻

[1]在比較和發現中探尋數學本質——《倍數和因數》教學新設計.

[2]適時滲透靈活嫁接——《倍數和因數》教學及思考.