回到本真，回到簡約

林穎勤

肖慧老師，言不多，行干練，就如她的教學風格一樣“簡”、一樣“真”。她所言的“求簡，求真，求深”，是對數學核心素養課堂的思辨，對數學教育真諦的追求，它能使數學教育回歸本真，讓學生獲取真知真能。在研究與實踐中，筆者再次獲得新的認識：教育教學中的簡約，既是一種策略又是一種形態還是一種境界，其本質就是要遵循教學規律和人的成長規律，以達到教學最大效益的育人功能。筆者在數學課堂上也常思考：學生到底需要怎樣的數學？怎樣的數學課堂才能喚醒童真童趣，讓學習回到本真、讓教學回到簡約？下文結合實例談談筆者的粗淺經驗及做法。

一、數學，“簡單”又好玩

一提到數學，不少學生都會想到“枯燥…‘恐怖”“焦慮”等詞語。作為一線教學工作者，我們一直在努力挖掘數學的真，展現數學的美，催生教學發生本質的變化，讓數學不再“可怕”。

（一）學科融合。鍛煉思維

六年級下學期的學生進入總復習階段時，舊知再探顯得“翻熱飯菜”無味道。基于活躍課堂、呼喚學生的童心，筆者設計了這樣一道題目：不允許使用梯子、凳子，請測量教室的容積。不出所料，學生一下子就合作完成了測量教室長、寬的數據，面對著教室的“高”，究竟如何出手呢？數學的魅力，就在于讓學習成為當下解決實際問題的需要，學生在想法子的同時需要打破學科的界限，讓學科交流、融合。然而，面對著新的任務，學生你一言我一語，這也是展示小組合作學習的最佳時機。以下為小組內的討論片斷展示：

生1：我們可以搭人梯，一個接一個，然后用軟尺進行測量！

生2：太危險了，何況題目里規定不能使用梯子！

生3：我們用棍子綁好，頂在天花板，再測量棍子的長度。

生4：去科技室借用小飛機粘上絲帶飛上天花板，再測量絲帶的長度。

生5：用手機將課室的墻壁拍下，然后測量。

討論一度陷入困境，師感嘆：“如果我們能飛上去就好了！”話音剛落，不知哪個角落傳來了一個小聲音：“我們找科學老師去！可以利用氫氣球幫我們飛上去測量啊！”整個數學課堂就這樣被“翻轉”了。于是，延伸到第二節課，學生請來了科學教師。玩過氫氣球的學生有一定的認識，但對于為什么“氫氣球能飛上天而空氣球不能”就一片茫然。為此我們進行了氫氣性質的知識拓展。學好了方法，接著又如何開始實施呢？“需要有步驟，不然就亂了。”學生經過思量，小組再次合作，嘗試做學習單，集體分享后再修改學習單。集思廣益，最好優化方案：將繩子拴在氫氣球上——測量氣球的長度——測量繩子的長度——把氣球和繩子長度加起來。在測量過程中，學生習慣性進行分工合作、興致盎然。“畦，畦，成功飛天啦！”隨著一聲聲驚嘆，兩個氣球同時成功地飛到了天花板，研究的熱情加溫了。學習單、黑板很快被寫滿數據。學生自己反思：“為什么每組數據相差那么遠呢？”在稚嫩的笑聲中他們發現了：“我們組的氣球結沒有打好，漏氣啦！”“我們在測量氣球的高時每放好尺子，測偏了。”“哈哈，你們組漏加氣球的長度啦！”……

歡聲笑語中，誰還覺得“數學可怕呢”？

陶行知先生認為，在做中教乃是真教，在做中學乃是真學，“教學做合一”的思想就是強調學生需在實踐中去追求真理。這樣的學科“混搭”，讓學生收獲了快樂、鍛煉了思維，也驗證了肖慧老師“學為中心，提升素養”的教學主張。

（二）游戲融合。拓展空間

教學的空間決定了學生發展的可能，給學生思考的空間、表達的空間、交往的空間、實踐的空間。然而，有學者做了這樣的比喻：在兩米高的小屋里，籃球運動員姚明再怎么努力也無法站直，因為他的頭早已頂住了天花板。試問在教學領域，教師對學生發展的“天花板”卻可能視而不見：小步零碎的提問、過于細膩的指導、以熟練為目的的刷題訓練等，這些直接禁錮了學生應有的數學思維。那么，“怎么教”也決定了“教什么”。狹窄的小屋，學生還能挺起自由思考的脊梁嗎？

筆者認為，如果將數學學習活動與學生的生活密切聯系，不僅可以幫助學生真正理解數學內容，也能夠促進學生運用已有的經驗實現“沖破天花板”的可能性。那如何將有趣的游戲與數學融為一體展開教學呢？下面，筆者以《億以內數的認識》為例進行分析。

1.每個數位站一位拿著數字卡片的人，另派一人拿著數字卡片與個位的人猜拳。猜贏后，和拿十位的人猜拳，直到猜輸為止，就把數字卡片交給下一位，取代其的位置，形成新的多位數。

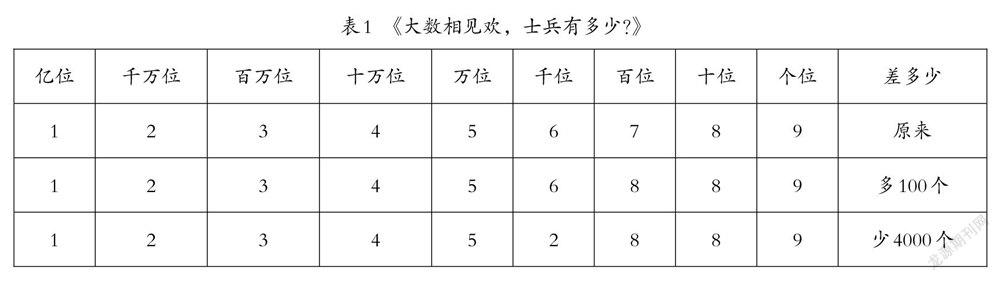
2.新的數與原來的數相差多少，寫在記錄卡上。（見表1）

3.根據表格回答問題：

（1）“多100個”是指將軍在哪個數位上猜輸了？

（2）“少4000個”是指將軍在哪個數位上猜輸了？

這個游戲融入了億以內數的認識的相關知識。學生可以自己制作數位卡片，進行分組，全班參與。臺上的學生進行游戲，臺下的學生進行記錄，并比較原來的數與新產生的數之間相差多少，從而讓學生在玩游戲的過程學習寫數、讀數，理解各個數位表示的意義以及兩個數之間的計算。

學科整合、數學游戲用簡單的方法表達數學，就是復雜問題簡單化，使用適合學生親近數學、學好數學的教學方式，是更為成功的教學。

二、數學，在互動中趨向“深度”

我們常發現，課堂上教師講解多、學生自主探索少的現象普遍存在。公開課上生生互動很流暢，殊不知這種形式都是課前經過精心安排、反復訓練來達到教師預設的目標。這樣的互動深度不夠，沒有給學生留下思考的空間和時間，學生像表演節目一樣，缺乏辨析、質疑能力。大部分學生學習較為被動，獲取知識常用“拿來主義”，沒有推動和創造。為此，筆者以《年、月、日》為例大膽嘗試放手，結合實情，在小組合作學習中將問題暴露出來。

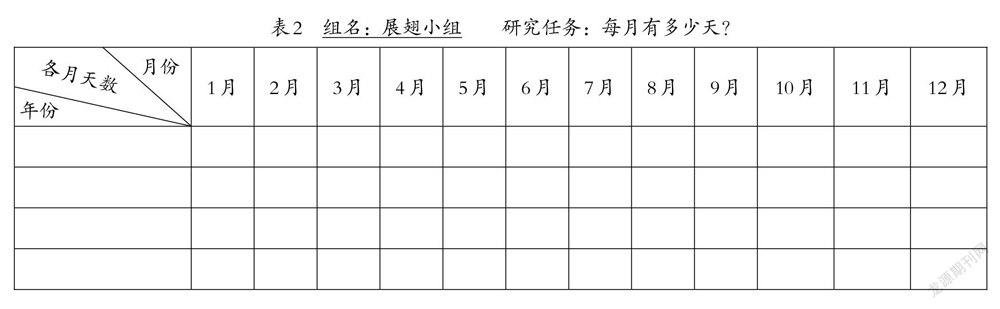
學生通過動手實踐、自主探索，進行了非常有個性的實踐和想法。經過小組內達成共識，上臺展示如以下任務卡。（見表2）

“學為中心”的課堂是學生做主人的舞臺。學生敢于提出質疑，表達自己的想法和疑惑，生生之間相互辯論解答，激起學生的思維碰撞的火花，是數學課最美麗的生態之花。這樣的課堂源于教師巧妙地提供舞臺，引導學生大膽質疑交流，教師要沉得住氣，善于把學生的質疑交給學生自己去解決。

師：大家討論得真激烈，哪個小組代表上來分享分享？

生1：我代表我們小組上來匯報，我們小組研究的是2005年至2008年，我們發現每一年的1月、3月、5月、7月、8月、10月、12月有31天。然后每一年的4月、6月、9月、11月有30天，就只有2月不同，2月有時候是28天，有時候是29天。

生2：因為我們發現2008后面的8能被4整除，其他的后面不能被4整除。能被4整除的是閏年，閏年的2月就有29天，平年的2月就有28天，平年就是不能整除4的。

師：真是豐富啊！同學們聽完匯報有什么想問？

生3：請問，為什么只是被4整除，而不是被5或被6整除呢？

生1：4的話，因為閏年四年才有一次。我的直覺認為除以4才有閏年。

生4：如果是2016年呢？

生1：2016年也是可以被4整除的。

生5：你的直覺有依據嗎？

生1：……

生6：我聽說是跟地球繞太陽公轉有關。

生2：圖書角課外書上有介紹，你可以看看。

生7：為什么有一些是31天，有一些是30天啊？

生1：我也不知道，估計是這樣分配的吧。

生8：為什么只把2月份定為28或29天，而不是3月呢？

也許學生的對話較為零散、幼稚，然而，核心問題就在學生的追問中，思維的碰撞中越辯越明。這不就體現了肖慧老師的主張“學為中心”的課堂，并不拒絕“教”，而是教學設計做減法，學生活動做加法，教師通過更高水平的教來促進教學了嗎？相信堅持下去，學生才會既樂于質疑又善于質疑，進一步內化思考，使學習的層次更趨向深度學習，對話更有質量。

三、數學。是文化的沉淀

《數學課程標準》指出：數學是人類的一種文化，它的內容、思想、方法和語言是現代文明的重要組成部分。因此，數學課堂教學不應只有抽象的數字、符號、運算和圖形，不應只是傳授數學知識，還應當讓數學文化走進小學數學課堂，使學生受到數學文化的熏陶，品味數學文化的魅力，提高數學文化素養。

（一）數學文化，培植數學情懷

將數學史引入課堂，筆者的做法是經常帶著學生欣賞古今中外的數學史料，祖沖之、阿基米德、高斯、華羅庚等數學大師，成了學生經常討論和崇拜的人物。筆者在教室里開辟一塊數學角，為學生創設數學文化的氛圍，為學生提供表達的園地。特設“數學小擂臺”“數學故事大王”，每周一上午數學課堂由不同的學生講述自己眼中的數學，分享自己課外的數學知識和趣事，講述自己崇拜的數學名家故事等等。

如當學生學習了《比的認識》一課，周末布置小任務：1.上網尋找“黃金比”的資料;2.你能用比的知識解釋“為什么女性總愛穿高跟鞋嗎？”。對于《圓的周長》的課外學習，學生的學習熱情更高漲，驚嘆于中國古代人民的偉大與智慧的同時，小組之間不約而同地展開背誦“圓周率”的小競賽。學生沉浸在數學文化中，思維已飛越了課堂、跨越了時空，萌生了探尋數學世界的積極情感。

（二）理性精神，涵養數學氣質

理性精神是數學文化的核心。理性，體現在數學追求一種完全確定、完全可靠的知識。著名華裔數學家丘成桐先生說“學數學是要有一點氣質的”，筆者以為，這種氣質乃理性精神無疑。數學課堂需要重視數學理性精神的涵養。下面，以《能被2、5整除的數的特征》一課，談理性精神的落地。

師：為什么判斷一個數是不是5的倍數，只要看個位？獨立思考、同桌交流之后全班交流。

生1：我發現5的倍數末尾一定是0或5，而這兩個數除以5正好沒有余數。

生2：奇數乘5，它的個位一定是5;偶數乘5，它的個位一定是0，沒有其他情況了，所以只看個位。

師：以上說的都是為什么看個位，而不是“只看個位”。

生3：如果去掉個位的話，就是一個整十、整百、整千數……這些數一定是5的倍數，所以十位就不用管了。

師：誰聽懂了他的想法？

生4：他的意思是，減去個位余下的數，個位一定是0，它能被5整除。

師：很好！誰能結合例子或教具進一步說明？（呈現計數器）

生5：在計數器的十位上撥2，表示2個10，20是5的倍數，所以十位上的2不影響結果。

生3：當個位是0，我在十位上任意撥，它們都是5的倍數。

生6：在百位、千位上任意撥，它們都是5的倍數，因為它們的個位都是0。

生7：一個數可以分成兩個部分，十位以上的部分必然是5的倍數，所以不用考慮;個位這個部分不確定，只看個位就好了！

師：數學是講道理的，同學們都是講道理的數學人！

數學課堂是傳承理性精神的主陣地，引領學生盡力去探求和明晰知識的最深刻最完美內涵，培養探究欲望和勇氣，是我們始終為之努力的目標。

煥發學生的學習本能，讓學習回到本真，讓教學回到簡約，我們期待遐見更美的數學。