學習數學的好工具—數形結合思想方法

褚慧

《數學新課程標準》指出：“在數學教學過程中滲透數學思想方法是落實讓學生獲得數學思想的課程目標的主要途徑。”數形結合思想是數學課程中蘊涵的重要的思想方法之一。學生領悟并掌握這一思想方法，很多數學問題便可以化難為易，化繁為簡，迎刃而解，因此，它是解決數學問題的十分有效的方法，是學好數學的工具之一。顯然，我們沒有開放專門的數學思想方法教學課，而是在日常的教學內容教學過程中逐漸滲透數形結合思想方法。在初中數學課堂中如何滲透數形結合思想方法？

一、深入認識數形結合思想方法

數形結合思想方法在數學教學中無處不在，我們通過實踐學習，可以感受到它的力量，它在數學學習中具有非常重要的作用。我國著名的數學家華羅庚先生說過：“數缺形時少直觀，形少數時難入微，數形結合百般好，隔離分家萬事休。”數能精確地揭示研究對象的數量特征，形能直觀地刻畫研究對象的空間結構，因此數形結合思想方法廣泛應用于數學學習過程中，也是中考中數學考查的一個重要數學思想。從初中數學教材的梳理分析中不難發現，在數與式，方程與不等式，函數，概率與統計等知識中都蘊含著數形結合思想方法。例如數軸，它是代數和幾何聯系的橋梁，利用數軸可以將有理數用點形象的表示出來，從而比較直觀地、簡明地解釋相反數、絕對值的意義，幫助學生們理解。不等式的解集也可以在數軸上直觀形象的表達出來。在初中數學教學中，有意識地滲透數形結合思想，使學生認識、掌握并應用這一思想方法有利于提高他們分析問題，解決問題的能力，也有利于拓寬他們解題的思路，對數學學習有著十分重要的意義。

二、積極培養數形結合思想方法的應用

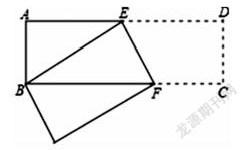
滲透數形結合思想方法應當與數學課程內容，數學解題活動的教學相結合。在數學課程中，數與形密切相關，我們要挖掘出教材滲透數形結合思想方法的教學內容，精心設計有意識地滲透，引導學生去感悟“數”與“形”之間的緊密結合，積極地實踐探索。對于幾何問題，要培養學生學觀察圖形，分析現象，從中獲得圖形中蘊含的代數關系，用代數方法去解決圖形問題的能力。例如：如圖長方形ABCD中，AB=3cm，AD=9cm，將此長方形折疊，使點 B與點 D重合，折痕為EF，則AE為多少？

這道題目我們可以設出AE的長，通過勾股定理的關系列出方程求出AE的長。在平面直角坐標系中圖形的平移問題，我們要將圖形中的點轉換成用數表示的點，通過推導數之間的關系來求點的坐標，我們可以讓學生經歷觀察、實驗、猜想、歸納的過程，引導學生將坐標系變化中數和形的變化緊密聯系起來，從而認識坐標變化與圖形變化之間的關系。這些過程都體現出以“數”解“形”的思想。同時，我們也要培養學生有意識地將“數”的問題轉化為“形”的問題來處理，以“形”究“數”。借助幾何直觀可以把復雜的數學問題變得簡明、形象，有助于探索解決問題的思路，預測結果。例如，我們研究正比例函數和一次函數的圖象和性質時，先讓學生掌握畫函數圖象的方法，使函數的性質形象直觀地顯示在圖象上，學生通過觀察圖象可以更好地理解量和變化規律，熟悉變量之間的關系，思考問題和解決問題會更加全面和深刻。有些函數問題可能要很復雜的解題過程才能求出結果，但是如果適時地加入圖象分析便可以通過圖象特征觀察得出結果。例如求一次函數y=2x+1圖象與一次函數y=-2x+3圖象的交點在第幾象限，我們不需要盲目的去解方程組，可以先畫圖象觀察便可以得出答案。

三、長期滲透數形結合思想方法

在初中數學教學中，我們要重視數形結合思想方法的滲透，引導學生把“數”與“形”完美的結合起來。初中生的思維發展正處于一個由具體到抽象，由低級到高級的過程，因此數形結合思想方法不是幾節課就能理解掌握的，需要一個長期、循序漸進的過程。我們在數學教學過程中，要有意識地讓學生去感悟數形結合思想方法，并逐步深化認識它，在探索交流中理解它，在解決問題中主動應用它，真正達到以“數”解“形”，以“形”助“數”，實現代數與幾何知識之間的轉化，獲得更大的收獲，從而促進數學能力和數學思維的發展。