基于改進型有限時間LQR的平衡車控制研究

劉銳軍　謝廣明　羅文廣

摘??? 要：針對平衡車啟動及停止時發生抖動的問題開展了相應的研究.通過建立系統動力學模型，設計了系統的改進型有限時間LQR（LQR， Linear Quadratic Regulator）控制器;對系統矩陣及控制矩陣進行改進，增加小范圍增量矩陣，系統能夠實現自適應調節，并使最優控制率在小范圍內可調，進而使性能指標達到最佳;通過仿真計算并選取最佳的加權矩陣[Q]和[R]，使性能指標達到最優.仿真實驗表明該方法具有可行性和實用性，解決了小范圍不穩定情況，有效克服了超調量過大而引起的不穩定.

關鍵詞：線性二次型;加權矩陣;最優控制器;MATLAB仿真

中圖分類號：U489;TP273??????????????? DOI：10.16375/j.cnki.cn45-1395/t.2019.02.005

0??? 引言

平衡車是電動車的一種，市場上的平衡車主要分為獨輪和雙輪兩種，其關鍵技術是動態穩定控制.就雙輪平衡車而言，傳統的平衡車是靠陀螺儀和加速傳感器來檢測車體的姿態變化，同時用伺服控制系統來驅動電機以確保系統的穩定.1985年日本提出了兩輪平衡車的模型，經過21世紀初的一個快速發展期，多個國家對該模型進行優化改進研究，主要有美國、日本、瑞士和法國等，直到2005年日本發布了“村田頑童”自行車機器人，該模型有了質的飛躍.國內關于平衡車的研究起步較晚，主要集中在高校，如：清華大學、西北工業大學等高校.目前平衡車的快速發展，也大力支持高校與企業之間合作及共同開展項目研究.

平衡車是在新產品的迭代創新過程中改進的.雙輪平衡車在啟動和停止時會出現抖動不穩的現象，需要一種控制方法來解決該問題，以確保其安全性.經典的線性二次型調節器LQR是一種具有較好魯棒性的控制器，其研究對象是現代控制理論中以狀態空間形式給出的線性系統，而性能指標函數為對象的狀態和控制輸入的二次型函數.LQR問題之所以受到普遍重視是因為它的應用不局限于某種物理系統，具有普遍意義且魯棒性較強.LQR最優控制器設計主要是求出狀態反饋控制的增益[K]，使二次型性能指標函數J取最小值，而[K]由加權矩陣[Q]和[R]唯一決定，故此[Q]和[R]的選擇尤為重要.本文將LQR控制器進行改進，以解決小范圍不穩定情況.該方法應用到雙輪平衡車上可以精確地檢測車身偏移角度，并結合精密的中央處理器下達指令使陀螺儀能夠及時調整車身角度，從而達到平衡控制[1].

1??? 雙輪平衡車系統建模

1.1?? 系統模型建立

雙輪平衡車簡稱移動機器人.近幾年研究的移動機器人有很多種類，包括：仿生的爬行機器人、類似動物運動的四腳機器人以及裝甲車式的履帶爬樓機器人等.這些機器人的發展為人們帶來了實際效益，同時也帶來了很大的方便.雙輪平衡車在實際生活當中應用最廣泛，例如，大型運動場、大型商場的治安員等都會用到雙輪平衡車來快速達到短距離目的地[2-3].

由于輪式機器人要比足式或爬行機器人的速度要高，因此需要輪式機器人在運動控制上具有較高的精度.這就要求控制器在設計上采用高性能控制策略，使其能夠在運行過程中進行準確的定位.以下根據平衡車結構建立系統模型，分析其動力學模型，并建立動力學方程[4-5].

1.1.1?? 對車輪建模

左、右車輪力學方程及轉動慣量為：

[MLXL=fL-TL]， [JLφL=CL-fLr]?????????????????????????????????????????????????????????? （1）

[MRXR=fR-TR]， [JRφR=CR-fRr]??????????????????????????????????????????????????????????? （2）

1.1.2?? 對擺桿建模

①水平方向的平衡方程為：

[mxP=TR+TL]??????????????????????????????????????????????????????????????????????????? （3）

其中，[xp=xm+Ssinθ]，[xp=xm+S（θcosθ-θ2sinθ）]

[xm=xL+xR2]????????????????????????????????????????????????????????????????????????????????? （4）

②轉矩方程為：

[JPθ=S（PR+PL）sinθ-S（TR+TL）cosθ]?????;????????????????????????????????????????? （5）

③垂直方向的平衡方程為：

[mxZ=-mg+PR+PL]??????????????????????????????????????????????????????????????? （6）

其中，[xZ=S（cosθ-1）]，[xZ=S（θ2cosθ-θsinθ）]

④平衡車在轉彎時的平衡方程為：

[Jψψ=（TR+TL）D2]???????????????????????????????????????????????????????????????????????? （7）

[ψ=-xR+xLD]???????????????????????????????????????????????????????????????????????????????? （8）

⑤兩輪平衡車的數學模型為：

[CR+CLr=xm（2J?r2+2M）-mSθ]???????????????????????????????????????????????????????????? （9）

[-mLxm=θ（mS2+JP）-mgSθ]????????????????????????????????????????????????????? （10）

[-CR+CLr=ψ（DM+2JψD+DJ?r2）]????????????????????????????????????????????????????????? （11）

由式（9）—式（11）可得平衡車系統方程如下：

[xxθθ=0001a210000010a41000θxθθ+b11b12b21b220000CRCL]??????????????????????????????????????? （12）

[ψψ=0100ψψ+b11b1200CRCL]????????????????????????????????????????????????? （13）

由于本動力學方程有兩個角度，必須滿足一定的條件才能成立，式（9）—式（11）是在假設當[θ]在[±5°]變化時（[±5°]變化是指平衡車內部IMU檢測擺桿內部機械的偏差，而非平衡車擺桿的傾斜度或車身的傾斜度.因IMU模塊檢測比較靈敏，故若檢測值偏離太大，反映在擺桿及車身的角度遠大于偏離值，因此[±5°]符合要求），[sinθ≈θ]，[cosθ≈1]成立，滿足該條件，從而[θ2≈0].

在平衡車中控制系統是關鍵的部分，整個車身的運行情況都由控制系統實現，因此，精準的控制系統設計是平衡車安全與否的關鍵.因為設計簡單便捷，市面上大多平衡車采用PID算法來控制.該算法應用到平衡車上，雖然能夠很好的利用其閉環系統實現控制，但在精準控制上難以保證，因此迫切需要一種控制器來實現精準控制.LQR控制器以其易于構成閉環系統、設計簡單及能夠較好的實現最優控制目的的優點，成為平衡車設計控制器的新方法.本文對LQR控制器進行了改進，增加微量調節反饋矩陣，使其能夠對啟動及停止時的微小抖動問題實現良好的控制.

2??? 平衡車LQR控制器設計

LQR即線性二次型調節器，LQR可以得到狀態線性反饋的最優控制規律，易于構成閉環最優控制，可在不消耗過多能量的情況下，保持系統狀態各分量仍接近平衡狀態.LQR最優控制充分發揮成本低這一特點，使其原系統達到較好的性能指標，也可以對不穩定系統進行調整.線性二次型問題解出的控制率可以通過狀態反饋實現閉環最優控制，成為當今控制工程領域中主要設計方法之一.

由于目前很多平衡車在啟動和停止時出現不可控制的抖動現象，導致車身不穩，對人身安全造成一定的危險，因此，本設計采用自加調節式系統控制，利用微小調節矩陣檢測偏移角度，從而矯正偏移量，使平衡車能夠在整體傾斜角度范圍內，通過自加調節式系統克服角度差，使車身能夠在偏離一定角度后立刻得到矯正.

2.1?? 傳統設計方案

狀態調節器的任務在于，當系統狀態由于任何原因偏離了平衡狀態時，能在不消耗過多能量的情況下，保持系統狀態各分量仍接近于平衡狀態.在研究這類問題時，通常是把初始狀態矢量看作擾動，把零狀態取作平衡狀態.因此，需要解決的問題是，尋求最優控制率[u]矩陣，在有限時間內將系統初始狀態轉移到零點附近.平衡車系統在當前狀態由于任何原因偏離了平衡狀態時，要在最短時間內，保持系統狀態各分量仍接近于平衡狀態，尤其在外部干擾情況下要求系統狀態轉移到零點附近.其系統滿足最優控制的線性二次型調節器.

①系統狀態方程為：

[x（t）=A（t）x（t）+B（t）u（t）x（t0）=x0y（t）=C（t）x（t）]?????????????????????????????????????????????????????????? （14）

②性能指標為：

[J=12eT（tf）Fe（tf）+12t0tf[eT（t）Q（t）e（t）+uT（t）R（t）u（t）]dt]???????????????????? （15）

其中，[A（t）]稱為狀態矩陣，[B（t）]稱為控制輸入矩陣，[C（t）]稱為輸出矩陣，[x（t）∈Rm];[u（t）∈Rm]，無約束;[y（t）∈Rl]，[0<l≤m≤n];輸出誤差向量[e（t）=z（t）-y（t）]，[z（t）∈Rl]，為理想輸出向量，要求確定最優控制[u?（t）]，使性能指標[J]取得極小值[6-7].在系統方程（14）和二次性能指標式（15）中，如果[C（t）∈I]，[z（t）=0]，則有：

[e（t）=-y（t）=-x（t）]???????????????????????????????????????????????????????????? （16）

那么將式（16）代入式（15）得性能指標為：

[J=12xT（tf）Fx（tf）+12t0tf[xT（t）Q（t）x（t）+uT（t）R（t）u（t）]dt]?????????????????????? （17）

式（17）即為狀態調節器的性能泛函.

構造哈密頓函數（Hamilton）

[H[x，u，λ，t]=12[xT（t）Q（t）x（t）+uT（t）R（t）u（t）]+λT[A（t）x（t）+B（t）u（t）]]??? （18）

從而得到：

[u?（t）=-R-1（t）BT（t）P（t）x（t）=-K（t）x（t）]?????????????????????????????????? （19）

其中，[K（t）=R-1（t）BT（t）P（t）]，[P（t）]可以通過黎卡提（Riccati）微分方程來計算.

[P（t）=-P（t）A（t）-AT（t）P（t）+P（t）B（t）R-1（t）BT（t）×P（t）-Q（t）]????????????????????????? （20）

式（17）中加權矩陣[Q是n×n]維半正定矩陣，[R是r×r]維正定矩陣;第一個積分項表示系統動態跟蹤誤差加權平均和的積分;第二個積分項表示系統控制能耗總量. LQR最優控制器設計主要是求出狀態反饋控制的增益[K]，使二次型性能指標函數[J]取最小值，而[K]由加權矩陣[Q]和[R]唯一決定，故此[Q]和[R]的選擇尤為重要.在本設計平衡車控制器中[Q]和[R]的選取主要取決于工程上的調試及結構設計，一般根據設計要求的不同來選擇[Q]和[R]的大小從而加以約束狀態量及控制量.

2.2?? 改進型的設計方案

①系統狀態方程為：

[x（t）=A+ΔA1（t）x（t）+B+ΔB1（t）u（t）x（t0）=x0y（t）=C1（t）x（t）]???????????????????????????????????????? （21）

其中，[A]和[ΔA1]為相同維數的矩陣，[B]和[ΔB1]也為相同維數的矩陣，[ΔA1]與[ΔB1]為不確定性矩陣，而這兩個矩陣分別是在外界干擾時所產生的，通過調節[ΔA1]與[ΔB1]來確定系統的穩定[8].增量矩陣[ΔA1]與[ΔB1]是通過平衡車的IMU檢測后反饋系統的差值，根據差值適當增加[ΔA1]與[ΔB1]矩陣以達到穩定的目標.增量矩陣不是無限隨意增加，根據平衡車抖動的范圍設定增量矩陣的界限，因此在檢測到偏差值后反饋給系統即可以確定增量矩陣大小，從而調節系統穩定性.

②相應的[u?（t）]及[P（t）]如下：

[u*（t）=-R-1（t）B+ΔB1T（t）P（t）x（t）=-K1（t）x（t）]???????????????????????????????????? （22）

[P（t）=-P（t）A+ΔA1（t）-A+ΔA1T（t）P（t）+P（t）B+ΔB1（t）R-1（t）B+ΔB1T（t）×P（t）-Q（t）]???&nbsp;?????????????????? （23）

3??? 仿真實驗及分析

3.1?? 仿真實驗數據選擇

式（24）—式（25）中，系統矩陣：[A+ΔA1];輸入矩陣：[B+ΔB1];輸出矩陣：[C1];輸入向量：[u];狀態向量：[X];輸出向量：[Y].

在實際仿真中各參數值的設定如表2所示.選取各參數值確定系統方程式（24）、式（25），使用數據分析計算軟件MATLAB進行仿真實驗.仿真結果分別以可視化圖形展示，圖2—圖6分別表示不同情況下的仿真結果[9-12].

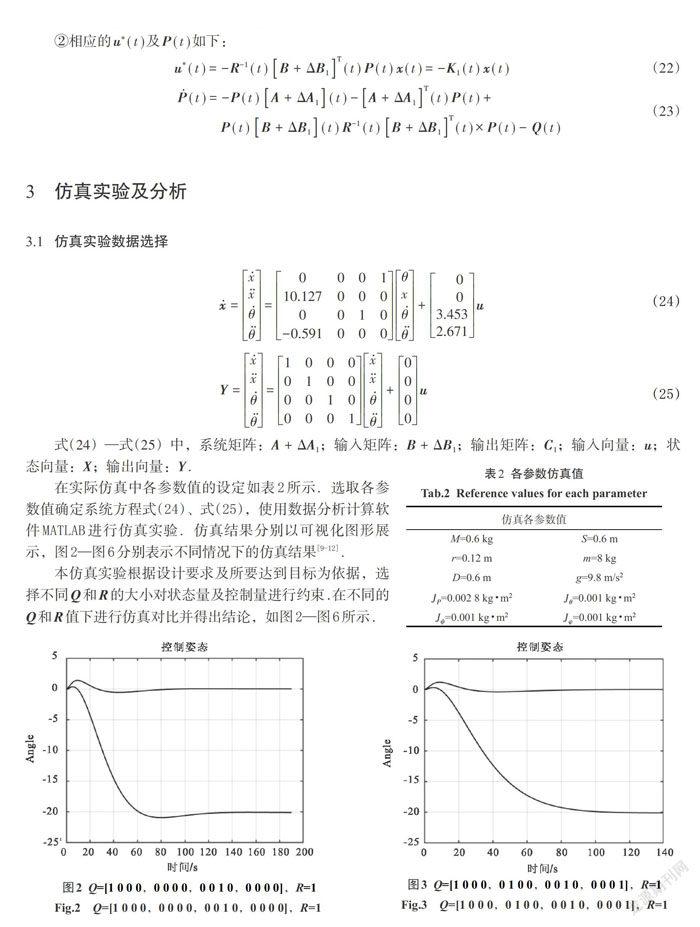
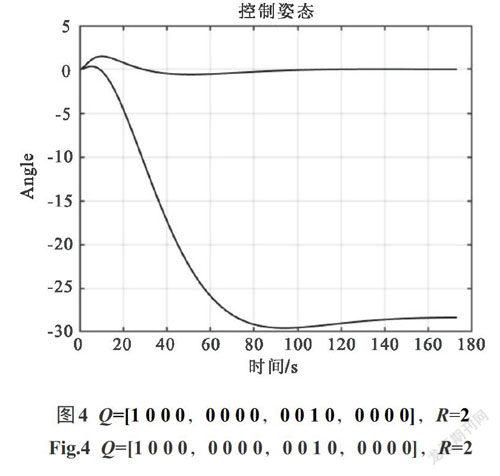
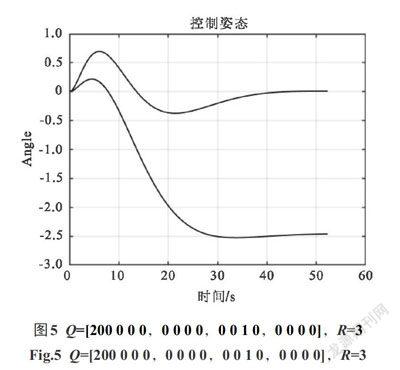
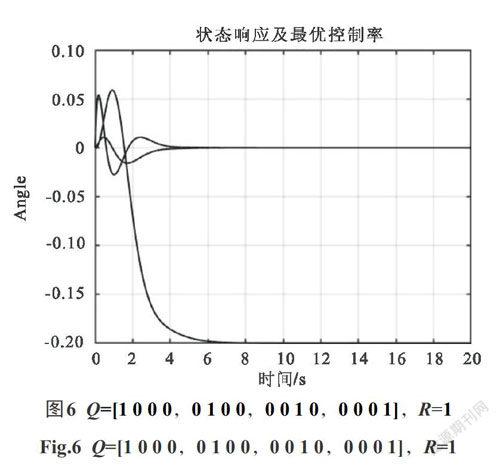
本仿真實驗根據設計要求及所要達到目標為依據，選擇不同[Q]和[R]的大小對狀態量及控制量進行約束.在不同的[Q]和[R]值下進行仿真對比并得出結論，如圖2—圖6所示.

3.2?? 仿真結果分析

由以上仿真實驗得知：解決雙輪平衡車在啟動與停止時小范圍抖動的問題，關鍵在控制器的設計，控制器的參數值是控制效果的直接決定因素.仿真中可以得出，改進型的控制器只要選定合理的參數就可以實現較短時間內達到穩定狀態.圖2和圖4代表加權矩陣[Q]相同而加權矩陣[R]不同的情況.從圖中可以看出在加權矩陣[Q]相同[R]不同時：當[R]越小，擺桿的擺幅偏離中心方向越小，而且到達穩定時間較短，并且[R]越小，會出現小范圍的超調量，但很快就恢復正常.圖2和圖3代表加權矩陣[R]相同[Q]不同的情況.這種情況下改變[Q]的單一向量會消除超調量，并且在控制擺幅相等時，穩定時間會更短.圖5表明同時選擇較大的[Q]和[R]會使平衡車出現明顯的超調量，而且穩定性無法得到控制.圖6是經過調試后確定的[Q]和[R]值，并得到的狀態響應及最優控制曲線.圖中可以看到平衡車在發生抖動時能夠很快得到控制并趨于穩定，控制效果很好，在該條件下[K]=[-12.541 9， -1.000 0， 20.282 2， -22.626 8].通過實驗仿真驗證了該方案的可行性，即：增加小范圍偏移防抖動矩陣有效解決了雙輪平衡車在啟動及停止時刻出現小范圍抖動的問題.

4??? 結束語

大量的仿真結果表明，當在系統中引入可調節控制矩陣時控制效果比傳統的效果好，并且可以較為簡單的實現調節功能.本文利用力學知識對平衡車進行系統建模，計算出系統方程;通過黎卡提（Riccati）微分方程來計算，從而得出P（t），進而計算出反饋矩陣.另外，在控制過程中[Q]和[R]的選取對控制效果有明顯的影響，而且二者是相互制約的關系，改變其中任何一個都會有較大影響，在多次試驗后選取了最優控制的加權矩陣[Q]和[R].文中雖然達到了控制效果，但還需改善達到最優控制的時間，才能使系統更加快速的達到穩定狀態，該方案將在實際工程中具有很好的參考與指導價值.

參考文獻

[1]???? 朱年華.兩輪自平衡電動車控制系統設計與研究[D].南昌：華東交通大學，2016.

[2]???? 牛伯冕.線性最優控制方法及其在旋轉倒立擺中的應用分析[J].自動化與儀器儀表，2018（2）：183-186.

[3]???? 楊正才，呂科.基于模糊PID控制方法的兩輪直立自平衡電動車研究[J].控制工程，2016，23（3）：366-370.

[4]???? 薛凡，孫京誥，嚴懷成.兩輪平衡車的建模與控制研究[J].化工自動化及儀表，2012，39（11）：1450-1454.

[5]???? 申鐵龍，梅生偉，王宏，等.魯棒控制基準設計問題：倒立擺控制[J].控制理論與應用，2003，20（6）：974-975.

[6]???? 段廣仁.線性系統理論[M].2版.哈爾濱：哈爾濱工業大學出版社，2004.

[7]???? 張曉亮，羅文廣.汽車主動懸架系統的線性二次最優控制研究[J].廣西工學院學報，2011，22（4）：44-48.

[8]???? 劉愛民，梁亞茹.基于修正型線性二次最優控制的PID參數優化方法及其應用[J].組合機床與自動化加工技術，2007（11）：36-39.

[9]???? 周加全，羅文廣，李亮，等.仿生機器魚位姿模糊控制研究[J].廣西科技大學學報，2017，28（2）：17-22.

[10]?? 謝超藝，羅文廣，張午昀，等.基于AD5435的永磁同步電機矢量控制系統仿真[J].廣西科技大學學報，2015，26（2）：8-13.

[11]?? PRASAD L B，TYAGI B，GUPTA H O.Optimal control of nonlinear inverted pendulum system using PID controller and LQR： performance analysis without and with disturbance input[J].國際自動化與計算雜志（英文版），2014，11（6）：661-670.

[12]?? ENDERLE J D，WOLFE J W. Time-optimal control of saccadic eye-movements[J].IEEE Transactions on Biomedical Engineering，1987，34（1）：43-55.

Design of optimal controller for balanced vehicle based

on improved LQR

LIU Ruijun1， XIE Guangming2， LUO Wenguang*1

（1.School of Electric and Information Engineering， Guangxi University of Science and Technology， Liuzhou 545006， China;2.Engineering School， Peking University， Beijing 100871， China）

Abstract： In this paper， a systematic study is made on the jitter problem of balancing vehicle when starting and stopping. The improved LQR （LQR， Linear Quadratic Regulator） controller is designed by establishing the system dynamics model. The system matrix and control matrix are improved to?????????? increase the matrix of small range increment， the system realizes the adaptive adjustment， and the??????? optimal control rate is adjustable in a small range so as to achieve the best performance index. The???? improved method solves the small-scale instability and effectively overcomes the instability of the?? overshoot. We can find the Q and R values that make the best performance by the simulation????????????? calculation of different Q and R. Through the simulation calculation and selecting the appropriate weight matrix Q and R， the performance index is optimized. Simulation experiments show that the method is feasible and practical.

Key words： linear quadratic; weighted matrix; optimal controller; MATLAB simulation