數學實驗：幾何概念學習的“腳手架”

匡金龍

摘要：數學實驗可以貫穿幾何概念教學的始終。教師要在實驗中引入，豐富圖形經驗：改圖，感悟圖形聯系;構圖，拓展視覺空間。要在實驗中探索，突出概念本質：選擇合適的素材，凸顯數學本質;厘清實驗序列，逐層建構意義。還要在實驗中聯結，深化概念理解：由淺入深，通過沖突澄清概念;由此及彼，利用變式溝通聯系;由表及里，借助反思促進聯系。

關鍵詞：數學實驗幾何概念教學引入探索聯結

數學實驗是為了探索數學知識，檢驗數學猜想或解決數學問題，借助一定的物質或技術手段，進行數學化操作的一種數學實踐探索活動。小學數學教學中的實驗，旨在引導學生通過操作、觀察、分析、猜想和推理等數學活動，經歷數學知識的“再創造”與“再發現”的過程，親身體驗數學，理解和建構數學。

《未來的幾何》一文指出，幾何對象和概念的學習，應該采用實驗與歸納的方法，而不是公理化的途徑。在幾何概念教學中，教師應該基于學生已有的數學經驗，借助數學實驗幫助學生經歷概念的形成過程，積累“做數學”的活動經驗，理解概念的本質特征，發展學生的空間觀念。數學實驗可以貫穿幾何概念教學的始終。

一、在實驗中引入，豐富圖形經驗

小學生在日常生活中已經積累了一定的圖形經驗，有觀察獲得的靜態經驗，也有通過折紙、尋找軌跡等活動獲得的動態經驗，兩種經驗共同構成了學生幾何概念學習的基礎。和“靜圖”經驗相比，小學生的“動圖”經驗相對比較缺乏。在教學中，教師應特別關注學生“動圖”經驗的積累，通過實驗動態地引入圖形，幫助學生感悟圖形和圖形要素之間的幾何關系。

（一）改圖，感悟圖形聯系

以熟悉的圖形作為認知起點，通過改變形狀引出新圖形，不僅能激發學生的學習熱情，而且能使學生清晰地感知到新、舊圖形之間的異同點，為學生進一步探索圖形特征，生成幾何概念的意義做必要的準備。拉、拼、分等都是改圖的方式。教學時，教師可根據實際需要，靈活選擇實驗的方式，幫助學生從圖形變化的角度積累直觀經驗。

比如，一年級學生認識平行四邊形時，受圖形感知水平的限制，往往把視覺上“長長”的四邊形誤認為是平行四邊形。教學時，教師可以通過操作長方形框架的實驗，將“長方形”變形而引出“平行四邊形”，幫助學生發現圖形之間的聯系和區別，以此加深對平行四邊形的認識。

（二）構圖，拓展視覺空間

通過平移、旋轉等方式動態建構圖形是常見的圖形引入方式。若運用巧妙，能取得意想不到的教學效果。受經驗和能力的制約，低年級學生還不能動態地從不同的角度考察圖形，只能看到整體的形狀，而不能明晰圖形之間或圖形部分元素之間的幾何關系。因此，教師要有意識地在中、高年級的幾何概念教學中引導學生構造圖形，發展空間觀念。

比如，教學“圓柱的認識”時，筆者讓學生以長方形紙片的一邊為軸旋轉一周引出圓柱——

設疑：長方形是我們學過的平面圖形，你能將這個平面圖形變成一個立體圖形嗎？

想象：如果以長方形紙片的一邊為軸旋轉一周，可能會得到什么圖形？

實驗：動手試一試，看看能得到什么圖形？有幾種情況？

從“靜態看圖”到“動態構圖”，拓展、豐富了學生對圖形的認識，幫助學生發現“形”和“體”之間的聯系，直觀感知圓柱底面“半徑”和“高”這兩個要素，為后續學習圓柱特征、體積積累必要的感性經驗;另外，引導學生經歷了“想象—實驗—多樣化呈現”的實驗過程，促進了學生空間觀念的形成。

二、在實驗中探索，突出概念本質

學生在日常生活中積累的直觀經驗，往往會受原有經驗、直觀原型以及認知背景等因素的干擾，難以生成概念，甚至造成概念誤解。教學時，教師可以精心設計實驗活動，排除非本質因素的干擾，突出概念的本質，促進學生對概念的理解。此外，控制實驗變量時，不僅要聚焦概念的本質要素，而且要觀照學生的認知心理，引領學生完成對概念要素的多元化認知，從而促進學生對幾何概念的深層次理解。

（一）選擇合適的素材，凸顯數學本質

實驗素材是實驗活動的物質基礎，是學生進行圖形操作和思維分析的對象，也是幾何概念形成的關鍵所在。因此，教師要以可視化、可操作性為依據，精心選擇實驗材料，提高其與概念本質要素的契合度。

比如，教學“圓的認識”時，一位教師設計了如下實驗活動：

設疑：你會畫圓嗎？會用什么工具畫圓呢？在還沒有發明圓規這個畫圓工具之前，古人是怎么畫圓的呢？（學生各抒己見，充分交流。）

組織實驗：利用一個圖釘，一條一端系著粉筆的繩子，能畫出圓嗎？動手畫一個圓。（提供兩套演示材料，一套中的繩子幾乎沒有彈性，另一套中的繩子是彈性較大的皮筋。）

展示與質疑：同樣是用“釘繩”畫圓，為什么有的畫出了標準的圓，有的畫不出呢？

提煉要點：用“釘繩”畫圓，一定要注意什么？（繩長固定不變。）

抽象定名：（1）圖釘所在的點正好在圓的中心，叫圓心;固定的繩長實際上是圓的半徑（邊說邊沿繩子描出線段）。想一想，半徑是怎樣的線段？（2）除了半徑，圓里還有一條特殊的線段，叫直徑。你知道直徑是怎樣的線段嗎？

描述特征：結合畫圓的過程思考，圓的半徑有什么特征？直徑呢？為什么？

這位教師沒有選擇常規的圓規畫圓，而是大膽選用了“釘繩”進行實驗。“釘繩”不是標準的畫圓工具，只是比較原始的畫圓素材，但在學生認識圓的特征過程中起到了關鍵的作用：首先，用“釘繩”取代圓規，特別是“繩子”的出場，使“圓心”和“半徑”這兩個要素都能以具象、物化的形式呈現，便于學生直觀感知和觀察分析;其次，利用不同彈性的“繩子”進行對比實驗，凸顯圓的本質特征;最后，“釘”“繩”直接抽象為“圓心”“半徑”，使實驗素材和數學概念無縫對接，加快了學生對圓的本質認識的進程。

（二）厘清實驗序列，逐層建構意義

心理學研究表明，學生認識圖形概念的過程是有一定順序的。就圖形概念的空間位置與度量性質來說，學生一開始往往只關注圖形的整體特征，隨后會按“先長度后角度”的次序注意圖形元素的單一性質，最后才能兼顧圖形元素的多種性質。教學時，教師要遵循學生認知圖形的規律，合理建構實驗序列。

比如，教學“認識長方形”時，一位教師設計了用小棒搭長方形的實驗活動：

出示3組小棒，如圖1。

實驗：請你選擇其中一組小棒搭一個長方形。

思考：（1）你選擇了哪組小棒？為什么？（2）你是怎樣擺放小棒位置的？

對比：如圖2，哪個搭成了長方形？同樣是把相同的小棒相對擺放，為什么②號圖形沒有搭成長方形？

猜想：根據用小棒搭長方形的過程，猜想長方形有什么特征？

實驗：測量長方形的邊和角，驗證猜想。

以上實驗活動，按從“邊”到“角”的順序引導學生逐步探索長方形的特征：首先，通過選材料搭圖形的活動，幫助學生從長度和位置這兩個維度描述長方形“邊”的特征;接著，就不同實驗結果進行對比觀察，突出“角”這個“弱刺激”，把學生的視角從“邊”順利引向“角”，實現對圖形元素的多元關注;最后，通過測量“邊”和“角”檢驗結論，一定程度上彌補了實驗的不足，提高了知識的嚴謹性。

三、在實驗中聯結，深化概念理解

數學概念之間具有廣泛的聯系，不僅有橫向的聯系和縱向聯系，而且有淺表性聯系和深層次聯系。幾何概念教學中，教師要基于對學生原有概念聯系的理性分析，通過生動、有趣的數學實驗幫助學生形成正確的概念“聯結”，深化對概念本質的理解。

（一）由淺入深，通過沖突澄清概念

受日常生活經驗的影響，小學生在學習幾何概念時經常會進行錯誤的概念“聯結”。凱斯認為，一個有效的教學策略是讓學生有機會主動察覺自己的錯誤，造成本身在認知上的不平衡，進而產生認知調整的需求。

比如，教學體積概念時，一位教師通過創設實驗情境幫助學生澄清概念：

準備：一個眼罩和兩個物體，其中一個物體是質量重但體積小的鐵塊，另一個質量輕但體積大的泡沫塑料。

實驗：先請一名學生帶上眼罩，雙手側平舉，再在該生的兩個手臂上各掛一種物體。

猜測：猜一猜，哪邊的物體體積大？為什么？

觀察：你有什么想法？（質量重的物體，體積不一定大。）

眾所周知，體積是物體所占空間的大小。但在實際教學中，我們發現小學生會用“質量”來解釋“體積”，認為質量重的物體體積大，反之，質量輕的物體體積小。針對這種簡單的、非本質的概念“聯結”，教師通過創設數學實驗情境，利用“視覺”和“體感”之間的差異制造認知沖突，幫助學生明確“體積”和“質量”的不同，進而明晰體積概念的本質。

（二）由此及彼，利用變式溝通聯系

研究表明，概念變式是從多角度檢查概念的方式，既能增強對概念的理解，還有助于概念的遷移。幾何概念教學中，教師可以巧借實驗提供圖形變式，通過變化圖形的本質或非本質特征，幫助學生把握概念的內涵和外延，同時促進圖形、概念之間的“聯結”。

比如，在“認識周長”的練習中，一位教師設計了如下實驗活動：

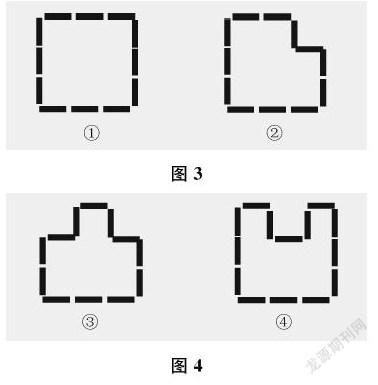
猜想：如圖3，圖①的周長是幾根牙簽的長度？圖①、圖②的周長哪個長？

實驗1：先照樣擺圖①，再把圖①變成圖②，思考圖①、圖②的周長哪個長，為什么。

猜想：如圖4，哪個圖形的周長長一些？

實驗2：把圖①分別變成圖③和圖④，思考圖③、圖④的周長一樣嗎，為什么。

發現：通過對實驗結果的觀察，你發現了什么？

學生通過操作牙簽變化圖形并比較圖形的周長，不僅能加深對周長本質的理解，而且能促進圖形、概念之間的“聯結”：一是滲透“轉化”的思想，建立各種圖形之間的內在聯系，積累通過轉化求不規則圖形周長的方法;二是引發對圖形“周長”和“大小”（面積）之間關系的思考。

（三）由表及里，借助反思促進聯系

恩格斯說過：“數學并不停止于實驗，而必須把它與理性的解釋結合起來，在這些看上去無聯系的實驗背后是否隱藏著某種理論？”幾何概念教學中，教師要鼓勵學生對實驗結果進行質疑，積極思考實驗背后的數學本質。

比如，教學“三角形按角分類”后，可以設計如下實驗活動：

質疑：按角分類，三角形只能分成直角、銳角和鈍角三角形這三類嗎？可不可能存在其他的三角形呢？

實驗：在釘子板上圍出含2個鈍角或2個直角的三角形。

思考：為什么圍不出其他的三角形呢？

針對三角形按角分為直角、鈍角和銳角三角形這個結論，教師首先通過提問“可不可能存在其他的三角形”對三角形的分類結果進行質疑，接著鼓勵學生通過“圍有2個鈍角或2個直角的三角形”，舉出反例驗證猜想，最后基于實驗事實引導學生深入思考現象背后的原因，從而幫助學生建立起“三角形內角和”與“三角形分類”之間的聯系，從本質上解釋并證實了三角形按角分類的合理性。

參考文獻：

[1] 鮑建生，周超.數學學習的心理基礎與過程[M].上海：上海教育出版社，2009.