基于光纖監測和PSO-SVM模型的馬家溝滑坡深部位移預測研究*

韓賀鳴 張 磊 施 斌 魏廣慶

(①地球科學與工程學院，南京大學 南京 210023)(②蘇州南智傳感科技有限公司 蘇州 215123)

0 引 言

中國是一個滑坡災害十分嚴重的國家，給人民的生命財產造成了巨大損失。因此，邊坡穩定性監測與評價對滑坡災害的防治顯得尤為重要。滑坡災害的發生通常伴隨著長期變形，滑坡位移的預測預報成為一種經濟高效的災害防治手段。

滑坡位移預測的準確度一方面取決于模型的優劣。自上個世紀60年代起，滑坡位移預測經歷了由最開始的經驗預測到后來的統計預測再到現在的非線性預測3個階段(許強等， 2004)。目前主流的非線性預測模型也由單一算法模型發展到多算法耦合模型，其中在非線性算法中PSO-SVM耦合模型在滑坡位移預測中已取得不錯的效果(張俊等， 2015)； 另一方面野外監測數據的質量也至關重要。目前滑坡預測模型中所采用的監測技術多為GPS技術。GPS數據只能監測表面位移，一方面精度易受環境因素影響，另一方面監測最小時間間隔為1個月左右，時間尺度較大導致預測的誤差較大，因此基于GPS數據進行的滑坡位移預測可能與實際情況存在較大差距。滑坡深部位移監測可直接有效地了解滑坡穩定性以及滑動面的發展規律(丁瑜等， 2011)。何滿潮(2009)指出：相比于表面位移監測，滑坡深部位移監測在滑坡位移預測中具有較高的準確度。2015年9月，作者所在的課題組研發了基于FBG技術的固定式測斜儀，并將其安裝在馬家溝滑坡滑帶處，由于無人值守光纖光柵解調儀的應用，該測斜儀可對滑坡進行遠程自動化監測和數據傳輸，其監測時間間隔為兩天，大大提高了滑坡深部位移監測的時間密度。

為實現滑坡深部位移的小時間尺度預測，本文將光纖監測的深部位移數據與PSO-SVM模型相結合，選取了2016.1～2017.9期間共計320個數據建立了預測模型。根據光纖監測數據得出與滑坡位移具有關聯性的影響因素，并利用時間序列法將位移的預測分為趨勢性位移預測以及波動性位移預測； 采用擬合法實現趨勢性位移預測，采用PSO-SVM模型實現波動性位移預測，預測結果較好。

1 基于FBG的滑坡深部位移監測原理

1.1 FBG基本原理

布拉格光柵具有對特定波長光反射的光特性，光纖光柵技術正是利用這種光特性實現傳感的，其工作原理及解調方案如圖 1所示(朱鴻鵠等， 2010)。當一束入射光進入時，布拉格光柵會反射特定波長的光。并且光柵所受的軸向應變和溫度的變化會影響到反射光的中心波長λB，其關系如式(1)所示(Othonos et al.， 2000)：

(1)

式中，λB為反射光的初始中心波長； ΔλB為中心波長的漂移量; Δε和ΔT分別為光纖所受的應變、溫度變化量;Cε和CT分別為布拉格光柵的應變系數和溫度系數，其取值約為0.78×10-6iμε-1和 6.67×10-6i℃-1。

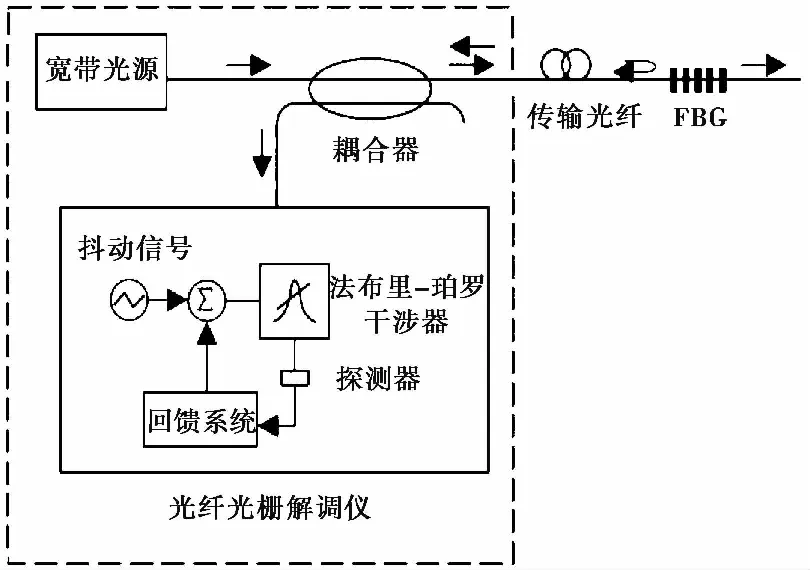
圖 1 FBG工作原理示意圖Fig. 1 Schematic diagram of FBG

因此當改變光纖光柵所受的溫度、應力、應變時，光柵的周期或纖芯折射率也隨之改變，從而反射光的波長發生了變化，通過將光纖所受應變和溫度的變化和波長改變建立對應關系便能實現對應變和溫度的測量。再通過參考光柵法分離溫度對應變測量的影響(劉漢平等， 2006)，從而實現應變的高精度測量。

1.2 滑坡深部位移光纖光柵監測原理

為了監測滑坡滑動面的分布和位移，本課題組與蘇州南智傳感科技有限公司合作研發了FBG傾角傳感器。如圖 2所示，在等強度梁上固定附有FBG的壓力膜，當傳感器發生傾斜時，重物的重力作用使梁彎曲，進而引起光纖光柵波長的改變。光纖光柵波長變化量與傾斜角度有一定的線性關系，通過室內標定試驗確定其線性系數，剔除溫度的影響后便可得到相應的傾角，進而通過勾股定理(其中L1為固定式測斜儀長度，L2為兩固定式測斜儀間鋼絲長度的一半)可計算出深部剪切帶的水平累計位移(汪其超， 2017)。

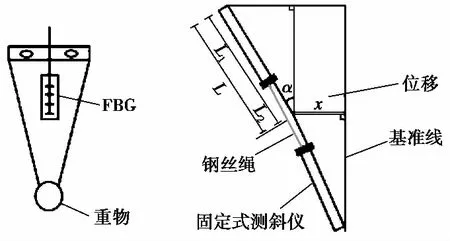
圖 2 FBG傾角傳感器原理示意圖Fig. 2 Schematic diagram of FBG inclination sensor

孫義杰(2015)通過分析兩年的光纖監測數據，精準地確定了馬家溝滑坡的滑動面位置。將傾角傳感器放置于滑帶位置，根據傾角數據和傳感器與滑帶的初始距離便可推算滑動面處位移值。

2 時間序列和PSO-SVM模型

2.1 時間序列加法模型

時間序列中的每個觀察值大小，是各種影響因素在同一時刻發生作用的綜合結果。依據時間序列加法原則，可將滑坡累積位移分為3部分，分別為受巖土體本身性質影響的趨勢性位移，以及受外界條件變化引起的波動性位移和受隨機因素影響的隨機性位移(姜諳男， 2007； 徐峰等， 2011)。由于目前難以對隨機因素的確定和監測，因此滑坡位移預測中不考慮隨機性位移。所以滑坡累計位移時間序列為：

st=ut+vt

(2)

其中，st為滑坡累計位移；ut為滑坡趨勢性位移；vt為滑坡波動性位移。

因此，目前常采用數值分析方法將趨勢性位移分離出來，進而實現對趨勢性位移和波動性位移的單獨預測，將兩者相疊加便得到滑坡位移的預測。

2.2 支持向量機和粒子群算法

支持向量機(Support Vector Machine， SVM)是Corinna et al. (1995)首先提出的，最初主要應用于模式識別領域中，隨著研究的深入，SVM在預測和綜合評價等領域顯現出很大的優勢。支持向量機回歸預測模型通常將樣本數據分成訓練集和測試集，利用合適的非線性映射將訓練集數據映射到高緯度空間，并在該空間進行線性回歸。這樣高維空間的線性回歸就和原始的非線性回歸相對應從而實現非線性回歸，并得到最優決策模型(Vapnik et al.，1996)。支持向量機原理見Zhou et al. (2016)。

粒子群優化算法(particle swarm optimization， PSO)是近年來發展起來的一種新的進化算法。從隨機解出發，通過迭代尋找最優解，并通過適應度來評價相應解的品質。這種算法與其他算法相比，具有實現難度低、精度高、收斂快等優點。其主要思想為：將每個待優化問題的解都視為搜索空間的一個粒子，被抽象為沒有質量和體積的微粒。PSO算法首先初始化一群隨機粒子(隨機解)，然后粒子們就追隨當前最優粒子在解空間中搜索，即通過迭代找到最優解。在尋找到局部最優解和全局最優解后，粒子會根據一定的公式更新自己的速度和新的位置。

圖 3 預測方法流程圖Fig. 3 Prediction flowchart ①模型的建立； ②模型的驗證； ③PSO-SVM模型的建立

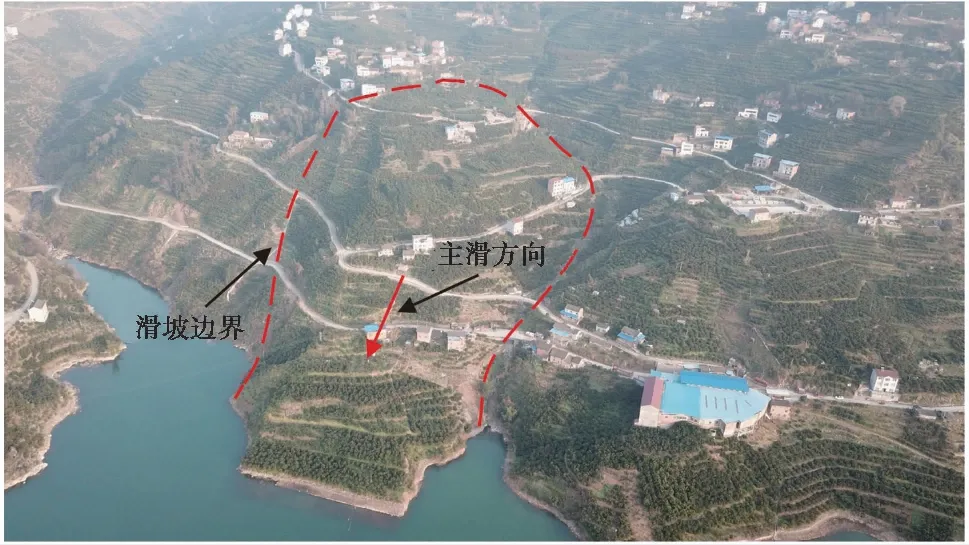
圖 4 三峽馬家溝Ⅰ號滑坡野外實景圖Fig. 4 Field picture of Majiagou No. 1 landslide in the Three Gorges

3 馬家溝滑坡深部位移光纖監測

3.1 馬家溝滑坡簡介

馬家溝滑坡的邊界大致呈舌狀，如圖 4所示，主滑方向為290°，與扎西河大致垂直。滑坡縱向長為537im，滑坡前緣和后緣的寬分別為150im和210im。滑坡整體較為平緩，滑坡面的平均坡度約為15°，從前緣到后緣其高程從135im到280im不等。馬家溝滑坡地層主要由上覆地層和下部基巖組成。上覆地層為松散且易透水的坡積物，主要由粉土夾雜著碎石組成。下覆基巖地層主要由細砂巖和石英質砂巖組成，其間夾雜著薄層的泥巖和粉砂質泥巖，遇水之后極易產生滑移。

課題組自2012年起建立馬家溝滑坡光纖監測網絡，監測效果良好，后因滑坡位移較大導致部分光纖監測孔超出量程無法測量。結合測斜管監測結果，馬家溝滑坡深部滑帶為其主要滑帶，如果馬家溝滑坡失穩，必將沿此滑帶整體滑動，所以對馬家溝滑坡深部位移的監測顯得尤為重要。因此，在2015年布設新的光纖綜合監測孔，并在深部滑帶處安裝了固定式測斜儀，通過FBG解調儀對滑坡深部位移實現了遠程監測。2012～2016年間的光纖監測數據采集間隔為4個月，從2016年1月起光纖光柵測斜儀監測數據采集間隔為兩天。根據以往監測結果可知，在滑坡12im及34im深度處存在著明顯變形，即潛在滑動面位置，與地層巖性等分析結果一致。

3.2 光纖監測數據分析

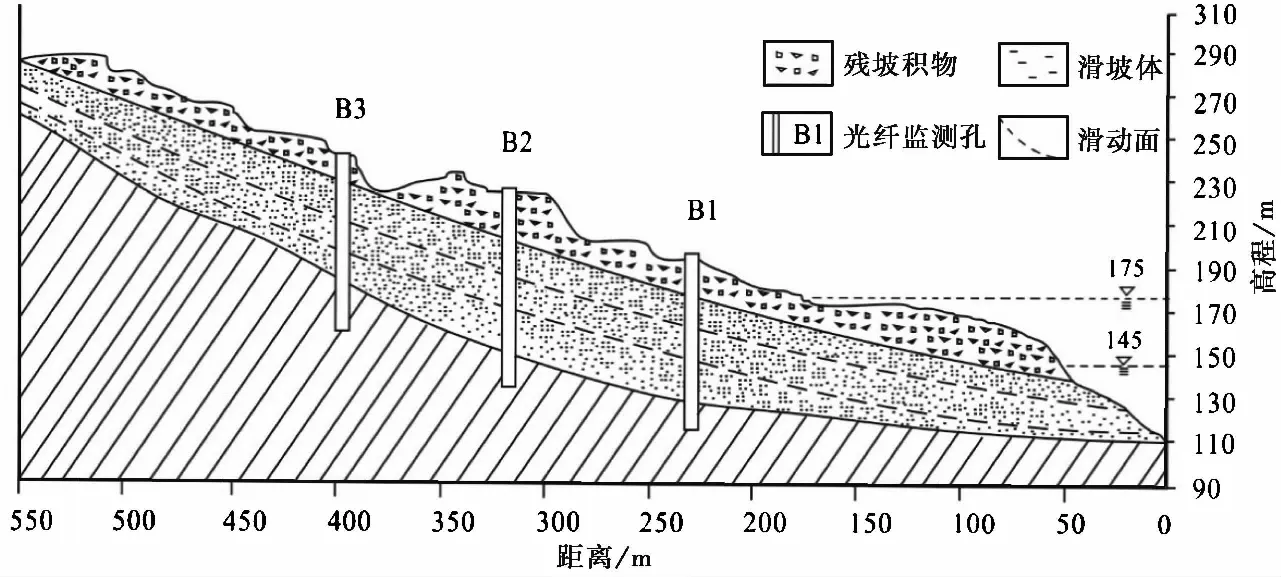
圖 5 三峽馬家溝地層剖面圖Fig. 5 Map of geological cross section of Majiagou

圖 6 馬家溝滑坡累積位移曲線Fig. 6 Cumulative displacement curve of Majiagou landslide

如圖 6馬家溝滑坡水平累積位移曲線所示，三峽馬家溝深部位移呈明顯階梯狀增長的特性。位移變化表現出不同幅度的緩增-陡增趨勢，在2016年5月到9月以及2017年7月到10月期間滑坡均出現了明顯的變形。其他時期滑坡位移呈平緩增長的態勢。由李曉等(2004)，代貞偉等(2016)，王魯男等(2016)研究可知，庫水位波動和降雨為主要影響滑坡變形的因素。因此本文主要分析庫水位和降雨量對滑坡深部位移的影響。

圖 7 累積位移與庫水位關系曲線Fig. 7 Relationship curve between cumulative displacement and reservoir level

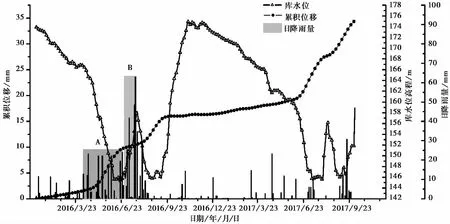
圖 8 累積位移與降雨量、庫水位關系曲線Fig. 8 Relationship curve among cumulative displacement， Rainfall and reservoir level

由降雨與位移關系圖 8可知，在圖中A段，降雨集中且降雨量大，滑坡也出現了明顯的位移； 但在圖中B段，庫區出現密集降雨的同時庫水位快速上升，滑坡位移卻處于穩定狀態。這表明滑坡的變形是受降雨和庫水位波動共同影響的，其中庫水位波動為主要影響因素。該發現也與揭奇(2015)的研究結果一致。同時在圖中A段，剛進入降雨密集區的一段時間內滑坡未出現明顯位移； 在B段雨季結束的一段時間，滑坡位移明顯增大。這表明降雨對滑坡的影響同樣存在著滯后性。

4 馬家溝滑坡深部位移預測

本文選取具有代表性的B2光纖監測孔共計320個數據進行預測，其中前270作為訓練集，后50作為測試集。

4.1 趨勢性位移預測

以往滑坡位移預測多采用大時間尺度，最小時間間隔常為1個月，時間跨度由5～10年不等(張俊等， 2015； 李驊錦等， 2016； 鄧冬梅等， 2017)。因此常采用移動平均法(張俊等， 2015)、EMD法(鄧冬梅等， 2017)提取一個相對較為平緩變化的函數曲線，或者采用低次多項式擬合一個平緩變化的函數曲線作為趨勢性位移。而本文選取的數據，最小時間間隔為兩天，時間跨度接近兩年，可以充分顯現出滑坡位移的具體變化以及和庫水位等影響因素的關聯性。但如果利用以上方法提取出較為平緩的趨勢性位移則會出現較大的誤差。因此針對本文所選取的數據，通過對比擬合的效果，選用三角函數來對圖像進行擬合的精度最高。因此選取前270數據點作為擬合樣本，基于matlab平臺的擬合工具對數據進行擬合。其函數表達式和主要的參數如下。擬合方程：

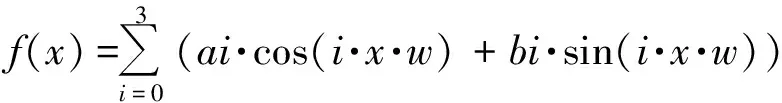
(3)

式中，w=0.7997； 擬合優度R2=0.9947;RMSE=0.6466(其他系數見表 1)。

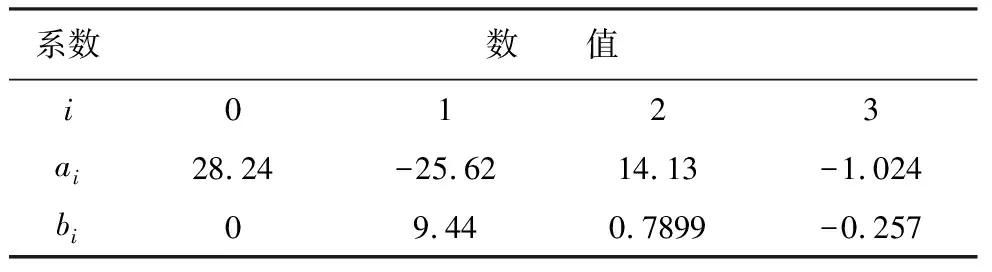
表 1 擬合方程系數Table 1 Fitting equation coefficients

之后再利用函數表達式代入進行后50個樣本點進行趨勢性位移預測，其結果如圖 9所示，趨勢性位移曲線整體呈現出陡增-緩增的特征。

圖 9 趨勢性位移預測結果圖Fig. 9 Results of trend displacement prediction

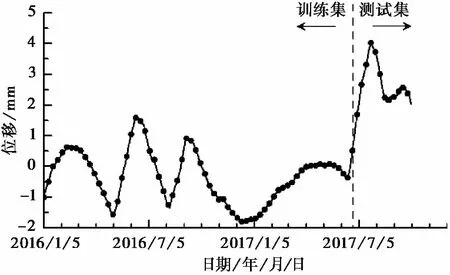
圖 10 波動性位移曲線Fig. 10 Fluctuant displacement curve

4.2 周期性位移預測

4.2.1 波動性位移提取

依據時間序列加法原則，波動性位移可由累積位移減去趨勢性位移得到。因此我們可以得到波動性位移的數據(圖 10)。我們同樣選取前270個數據點作為訓練集，后50數據點作為測試集。

4.2.2 影響因子的確定

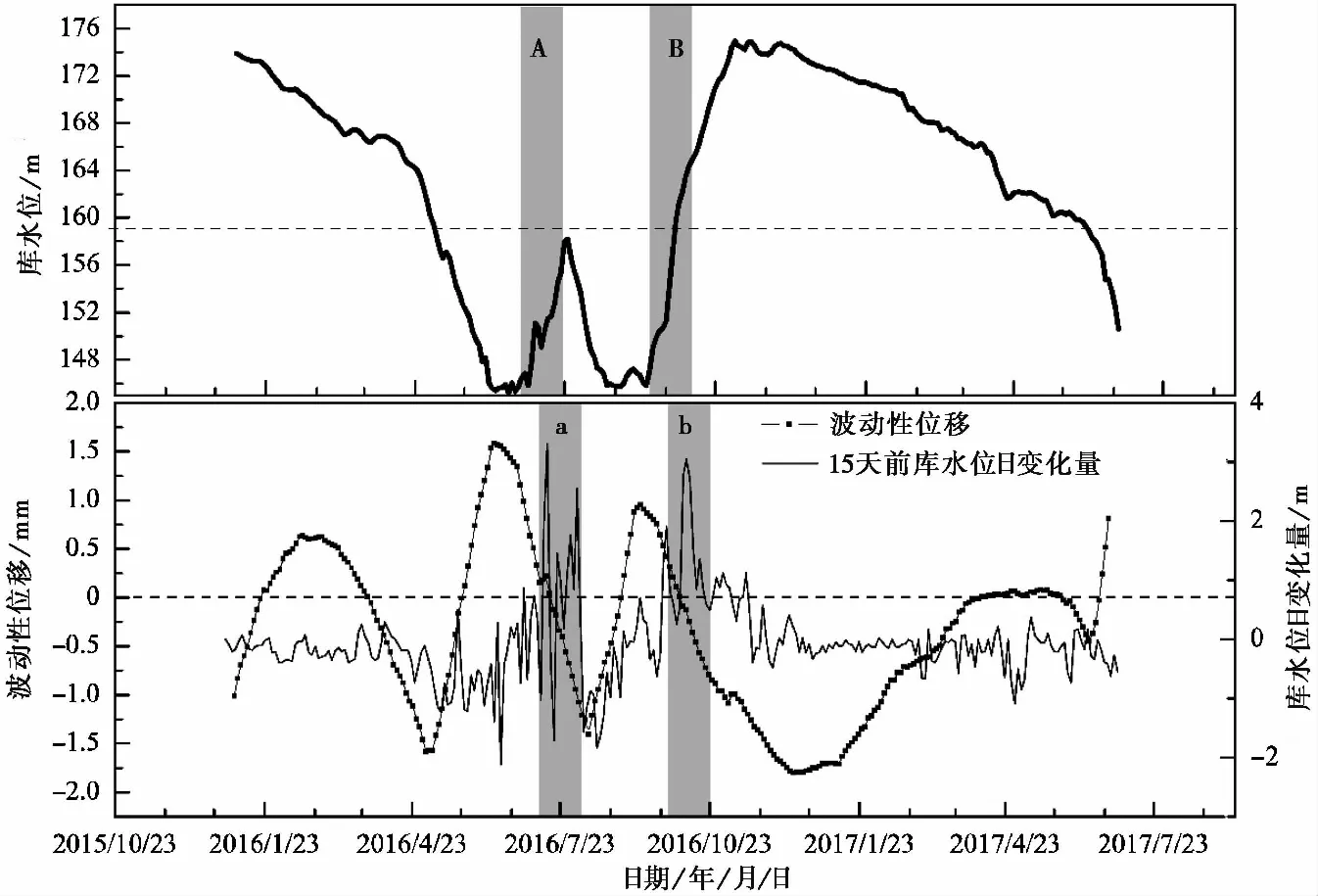
圖 11 波動性位移與半月前庫水位日變化量關系曲線圖Fig. 11 The graph of fluctuant displacement and daily variation of reservoir water level 15 days ago

由上述可知，三峽馬家溝深部位移主要受庫水位波動控制，庫水位變化會影響到滑坡深部的應力狀態、動靜水壓力、土體的抗剪強度等。三峽庫區庫水位具有明顯的日變化特征，同時從本文3.2節的分析可知，庫水位變化影響滑坡變形具有滯后性，且圖 7中a、b、c、d段出現位移變化滯后現象的時間跨度為15id左右。因此本文選取了15日前庫水位日變化量與波動性位移做對比，如圖 11所示，圖中A、B段為a、b段對應15id前的庫水位高程情況。在a、b段中， 15id前的庫水位日變化量變化較大且該時段的庫水位高程快速上升，波動性位移多為負值，即滑坡具有穩定變化的趨勢； a、b段的前期有一段波動性位移為正值，觀察A、B段我們可知，A、B段前是庫水位下降和上升的過渡段，位移變化出現滯后性，因此波動性位移為正值，即滑坡具有明顯位移。由以上分析可知， 15日前庫水位日變化量對波動性位移的影響符合實際情況。考慮本文數據時間跨度，對庫水位變化影響位移變化的滯后性的時間難以準確界定，因此再增加1個月前和2個月前庫水位日變化量作為模型的影響因子。

累積位移一方面反映了滑坡變化的總體趨勢，另一方面也反映了波動性位移的變化特征。因此，本文選取了月累積位移量和半月累積位移量與波動性位移作對比。如圖 12所示，A段曲線的變化趨勢相差較大，除此之外，變化趨勢較為一致。其原因是A段的累積位移長時間的平穩增加，較難反映出波動性位移的變化趨勢。但在累積位移變化明顯的階段，波動性位移也顯示了很強的關聯變化趨勢。

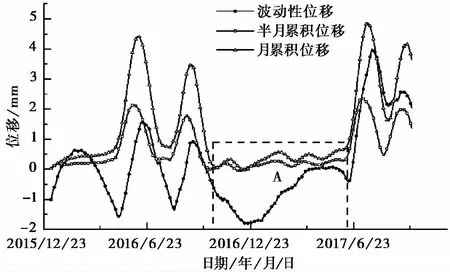
圖 12 波動性位移與半月、1個月累積位移關系曲線Fig. 12 Relationship curve among fluctuant displacement， two weeks， a month of cumulative displacement

由本文的光纖數據分析可知，降雨與庫水位共同影響滑坡的變形，且滑坡變形相對降雨量的改變具有滯后性，由圖 8中A、B區域降雨位移變化滯后降雨變化的時長約為15id，因此本文選用15日前日降雨量作為影響因子。但考慮到時間跨度只有兩年，期間降雨存在一定的偶然性。出于以上考慮，只選取一個降雨量的影響因子。

綜上所述，我們選用滑坡日累積位移，滑坡月累計位移，以及滑坡半月累計位移； 庫水位高程、15日前庫水位日變化量、1個月前庫水位日變化量、2個月前庫水位日變化量以及15日前日降雨量作為PSO-SVM模型的影響因子。

4.2.3 波動性位移預測

本文基于Matlab平臺，采用libsvm工具箱實現SVM的預測。首先將數據歸一化，通過將數據歸一化，提高了模型的運算效率。之后將數據轉化為libsvm的標準格式。在Matlab中，利用PSO算法進行最優參數的尋找，經過200次迭代后，得到最優懲罰因子C=11.2372和核函數參數g=3.9796。最后對訓練集進行訓練，得到模型后進行波動性位移的預測。將其與實測數據相對比，結果如圖 13所示。計算其均方根誤差(RMSE)和平均絕對百分誤差(MAPE)分別為0.51imm和0.37imm，預測效果較好。

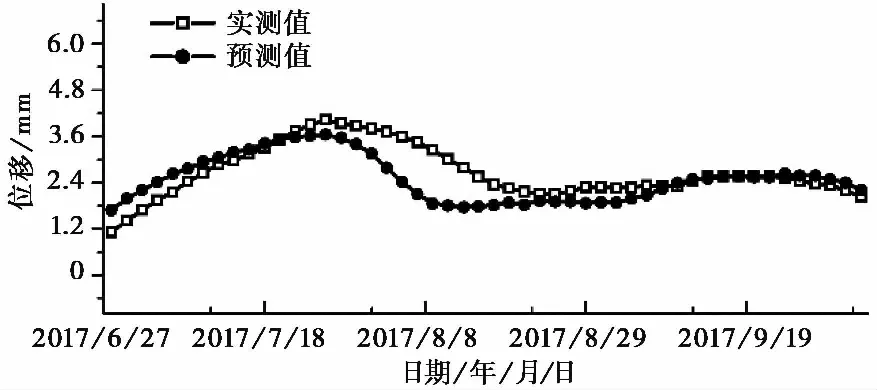
圖 13 波動性位移預測值與實測值對比圖Fig. 13 Comparison chart of predicted and the really measured fluctuant displacement

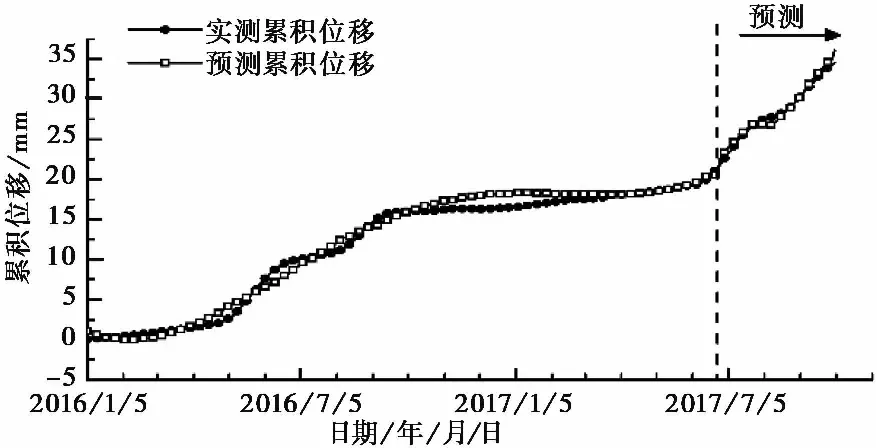
圖 14 總位移預測值與實測值對比圖Fig. 14 Comparison chart of predicted and the really measured displacement

4.3 累計位移預測

如圖 14所示，波動性位移和趨勢性位移相加便得到累積位移的預測值。對比實測值和預測值并計算其相關系數為0.98，均方根誤差為0.54imm，得到了很好的預測結果。

5 結 論

本文通過將光纖監測技術與PSO-SVM模型相結合的方法對馬家溝滑坡深部位移進行預測，得到以下結論：

(1)光纖監測技術具有精度高、抗干擾性強等優點，通過確定深部位移主要影響因素，可以實現高精度的滑坡位移預測。從本文中的預測結果來看，預測值和實測值較為一致，預測精度較高。說明光纖監測技術和PSO-SVM模型結合的方法能很好的應用于滑坡位移預測。

(2)通過建立時間間隔為兩天的預測模型，實現了小時間尺度的位移預測。大時間尺度的位移預測受隨機因素影響較大，并且不能反映位移在小時間尺度上的變化。本文通過PSO-SVM模型對小時間尺度的成功預測說明了PSO-SVM在小時間尺度預測中同樣有著很好的適應性。

(3)馬家溝滑坡深部位移主要受庫水位控制，具體表現為：當庫水位高程處于159im以上時，庫水位的變化對滑坡位移影響較小，滑坡深部位移呈現平穩變化趨勢； 當庫水位高程處于159im以下時，庫水位的上升和下降段，滑坡位移分別呈現平穩變化和顯著變化的趨勢。