隧洞涌水量預測計算方法研究進展*

吳 建 周志芳 李鳴威 陳 朦

(河海大學地球科學與工程學院 南京 211100)

0 引 言

在水利、交通、地下儲油洞庫、煤炭開采等各類工程中，均涉及到隧洞或地下洞室的開挖，而隧洞涌水是工程建設中一個突出的災害問題，大量的涌水會造成隧洞失穩(wěn)、人員傷亡、地面沉降及環(huán)境惡化等一系列惡劣后果(郭旭晶等， 2008； 劉志春等， 2015)。鑒于隧洞涌水問題的重要性，國內(nèi)外學者研究出大量的涌水量計算方法，如確定性方法：水均衡法、地下水動力學法、數(shù)值計算法、物理模擬法； 非確定性方法：水文地質(zhì)比擬法、模糊數(shù)學模型、BP人工神經(jīng)網(wǎng)絡和灰色理論等(朱大力等， 2000； 凌成鵬等， 2007； Katibeh et al.，2009； Zarei et al.，2013； 趙貴清等， 2017)。但不同的計算方法具有不同的適用條件和優(yōu)缺點，因此選取合理的計算方法對涌水量計算結果的準確性至關重要。

本文將國內(nèi)外廣泛應用的涌水量預測計算方法分為4類：經(jīng)驗公式法、解析公式法、數(shù)值計算法和物理模擬法。經(jīng)驗公式法包括SGR法、TIC法、大島洋志公式、佐藤邦明公式與鐵路勘測規(guī)范經(jīng)驗公式等(朱大力等， 2000； Katibeh et al.，2009； Zarei et al.，2013)； 這類方法多來源于工程實踐的總結，對于相似地質(zhì)條件下涌水問題計算有著不錯的預測精度； 解析公式法分為鏡像法、豎井法、保角變換法以及其他方法(Goodman et al.，1965； 王建宇， 2003； Park et al.，2008； 朱成偉等， 2017)，這類方法具有嚴密的理論推導過程、計算過程簡潔、便于工程應用； 數(shù)值計算法主要包括有限單元法、有限差分法、離散單元法、邊界元法和有限體積法等，這類方法適用于復雜水文地質(zhì)條件下隧洞涌水量問題的計算； 物理模擬法主要包括水電模擬、室內(nèi)物理模型實驗和現(xiàn)場示蹤試驗等(曾亞武等， 2001； 王克忠等， 2009； 高飛等， 2012； 方良成等， 2013； 萬繼偉等， 2017)，這類方法可以直觀顯現(xiàn)出隧洞涌水過程。此外，對于一些非確定性方法如水文地質(zhì)比擬法、模糊數(shù)學模型、BP人工神經(jīng)網(wǎng)絡和灰色理論等，適用于隧洞開挖完成后，根據(jù)監(jiān)測數(shù)據(jù)反演分析隧道實際涌水量，并對未來涌水趨勢作出預測(王建秀等， 2004)。

本文對上述4種計算方法詳細地闡述各自的原理與適用條件，比較不同方法之間的優(yōu)缺點，并提出當前亟須解決的問題，為下一步涌水問題的深入研究打下基礎。

1 經(jīng)驗公式法

1.1 常用經(jīng)驗公式

常用隧洞涌水量經(jīng)驗公式有大島洋志公式、佐藤邦明公式和鐵路勘測規(guī)范經(jīng)驗公式等，如下：

1.1.1 大島洋志公式

(1)

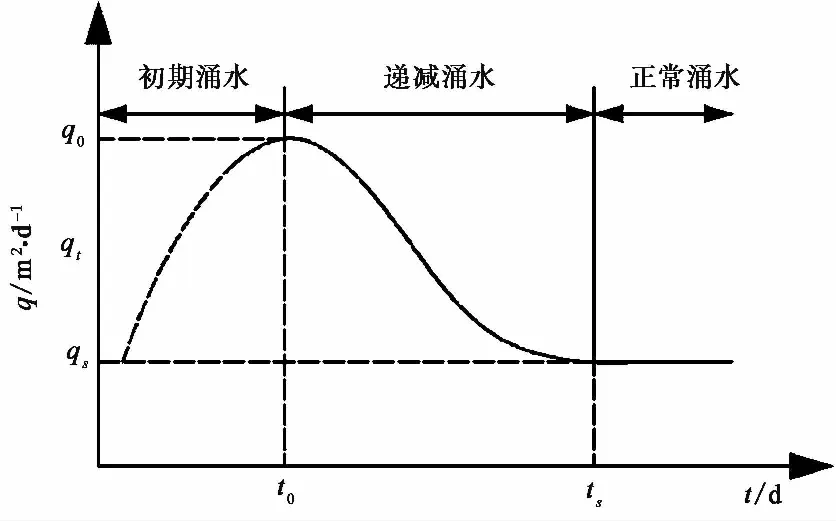
圖 1 隧洞涌水量隨時間變化曲線(朱大力等， 2000)Fig. 1 Water inflow into tunnels with time(Zhu et al.，2000)

1.1.2 鐵路勘測規(guī)范經(jīng)驗公式

(2)

式中，qs為隧洞單位長度正常涌水量(m2·d-1)(圖 1)； 其他符號含義同前。

1.1.3 佐藤邦明公式

(3)

式中，qt為最大涌水量衰減至某時刻ti的遞減涌水量(m2·d-1)(圖 1)；H為含水層厚度(m)；μ為含水裂隙巖體裂隙率；B為襯砌前隧道洞體寬度(m)；ti為最大涌水量至正常涌水量之間的任意遞減時間，其他符號含義同前。此外，還有裘布依公式，落合敏郎公式、科斯嘉公式、福希海默公式等(王振宇等， 2009)。

表 2 隧洞涌水速率分類方法(Zarei et al.，2013)Table 2 Tunnel inflow classification(TIC)，rating and correspondence inflow(Zarei et al.，2013)

1.2 現(xiàn)場綜合評價方法

傳統(tǒng)經(jīng)驗公式在計算過程中僅僅考慮初始地下水位、隧洞幾何尺寸、巖體滲透系數(shù)等幾個單一參數(shù)，忽略了巖石類型、降水量、隧洞埋深、裂隙開度等其他影響因素。此外，傳統(tǒng)經(jīng)驗公式將含水層視為均質(zhì)各向同性，這一初始假定無法適用于裂隙巖體，造成解析計算結果與實際偏差很大。基于上述存在的問題，Katibeh et al. (2009)從隧洞涌水危害程度的角度出發(fā)，根據(jù)10種隧洞涌水案例，總結了影響涌水量的7種因素，提出了一種現(xiàn)場涌水量評級方法(SGR法)，表達式如下：

SGR=[(S1+S2+S3+S4)+S5]×S6×S7

(4)

式中，S1～S7為7種影響因素的無量綱參數(shù)，分別為節(jié)理頻率和開度、片理、巖體破碎帶、喀斯特巖溶程度、土體滲透系數(shù)、隧洞水頭高度和年平均降水量，SGR法隧洞涌水量劃分區(qū)間見表 1。

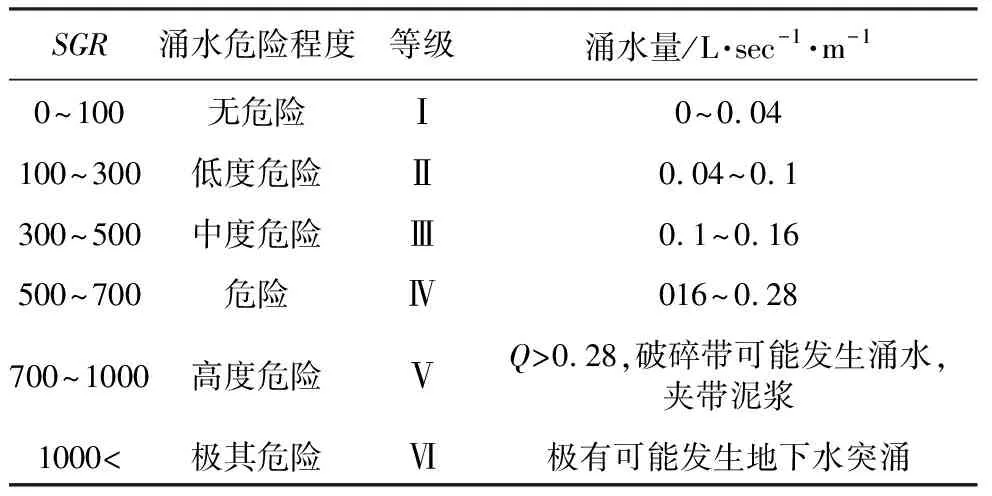
表 1 現(xiàn)場涌水量評級方法(Katibeh et al.，2009)Table 1 SGR rating for groundwater inflow to tunnels(Katibeh et al.，2009)

Zarei et al. (2013)統(tǒng)計了伊朗地區(qū)大量的隧洞涌水案例(33例)，建立了基礎數(shù)據(jù)庫，考慮到影響涌水量的5種主要參數(shù)：巖體組成結構(RMC)、巖石類型(RT)、黏土含量(CBC)、無側限抗壓強度(UCS)、隧洞埋深(TD)，利用層次分析法(AHP)和統(tǒng)計分析方法賦予5種影響參數(shù)不同的權重，提出了一種關于隧洞涌水速率的分類體系方法(TIC法)，并運用TIC法(表 2)計算出Long Zagros隧洞涌水量，與實測數(shù)據(jù)對比，證明了該方法的合理性和可操作性。

Maleki(2018)最新提出了一種確定裂隙巖體中隧洞涌水量的計算方法(GSR法)，該方法可以計算出3種不同情況下隧洞涌水量：地下水流入整個隧道區(qū)域、地下水流入隧道的單獨倉段及地下水流入隧道有效鉆進長度。GSR法計算公式如下：

(5)

式中，aF(J)為野外實測裂隙寬度(mm)；αJ為裂隙走向與隧道軸線之間夾角(°)；CJ為裂隙與隧道沿隧道軸線方向相交的長度(m)；SJ為裂隙間距(m)；H為地下水位至隧道底部高度(m)；J1，J2…Jn為裂隙分組。GSR法的不足之處在于無法精準地描述巖體出露特征與破碎帶長度，且忽視了斷層帶等復雜地質(zhì)構造對涌水的影響。

上述方法(SGR法、TIC法及GSR法)多來源于工程案例的總結，它們的思路往往是從統(tǒng)計學角度入手，收集并整理影響隧洞涌水量的多種參數(shù)，并從中發(fā)現(xiàn)一定的規(guī)律，提出相應的經(jīng)驗公式。這類方法相比較傳統(tǒng)經(jīng)驗公式，綜合考慮各種因素計算結果更符合實際，但不足之處在于需要前期大量的工作與詳細的實測數(shù)據(jù)，耗時久。

2 解析公式法

2.1 鏡像法

鏡像法的實質(zhì)是將隧洞半無限滲流場轉化為2個無限滲流場的疊加，邊界條件簡化處理(圖 2)。實際隧洞為“匯”，虛擬的對稱隧洞為“源”，地下水流線方向由源指向匯，源的流出速度等于匯的流入速度，根據(jù)隧洞地下水徑向流的對稱性，地下水位線為一個等勢面(應宏偉等， 2016)。Harr et al.(1963)利用鏡像法求解出適用于深埋隧洞涌水量解析公式，表達式為：

(6)

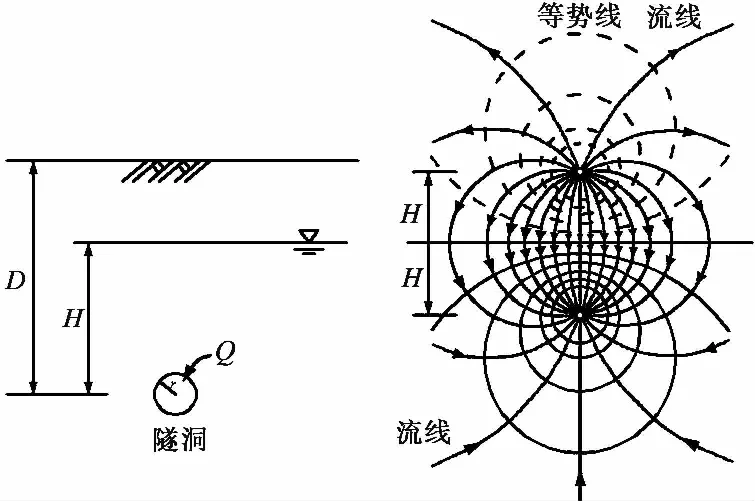
圖 2 鏡像法Fig. 2 Image tunnel method

Goodman et al. (1965)對公式進行了簡化，即當深埋隧洞H?r，式(6)可簡化為：

(7)

Goodman公式是當前應用最廣泛的公式，它適用于徑流條件下高水頭或深埋隧洞的涌水量計算，對于淺埋隧洞或裂隙介質(zhì)中隧洞涌水量的計算結果則往往偏大。

Zhang et al.(1993)假定隧洞處于海底或無限補給含水層之中，受到非均質(zhì)各向同性圍巖壓力，裂隙巖體滲透系數(shù)隨隧洞埋深增大而呈指數(shù)衰減變化，利用鏡像法推導出涌水量解析公式，表達式為：

(8)

式(8)考慮到一定地質(zhì)因素，初步解決了裂隙巖體中隧洞涌水量問題，但不足之處在于僅僅將裂隙巖體視為非均質(zhì)，而忽略其各向異性特性，同時公式無法進行變化水位條件下隧洞涌水計算。

Lei(1999)、Kolymbas et al. (2007)對Goodman公式進行了修改，拓展了其適用范圍，使其不再受到大埋深的限定，表達式為：

(9)

Karlsrud(2001)根據(jù)Oslo地區(qū)實際工程案例，結合野外實測數(shù)據(jù)與工程經(jīng)驗，引入經(jīng)驗系數(shù)修正了Goodman公式，使之更適用于實際工程運用，表達式如下：

(10)

上式適用于深埋隧洞，即隧洞埋深大于半徑的3～4倍。

Raymer(2001)修正了Goodman公式，并引入Heuer折減系數(shù)(1/8)，提出了淺埋隧洞涌水量的解析公式：

(11)

值得注意的是，Raymer公式是當今淺埋隧洞涌水量計算最廣泛的公式。

上述式(6)至式(11)僅僅計算出隧洞正常涌水量，無法適用于涌水量遞減狀態(tài)下計算問題(圖 1)，Hwang et al. (2007)針對隧洞遞減涌水問題，利用鏡像法與井流理論，將隧洞非穩(wěn)定變流量的涌水問題轉化為穩(wěn)定定流量的井流問題，提出了隧洞涌水量的半解析公式。

對于襯砌及注漿條件下隧洞涌水量計算問題，我國學者應宏偉等(2016)同樣利用鏡像法推導出解析公式，如下：

(12)

2.2 豎井法

豎井法通常基于地下水動力學理論，將半無限滲流場隧洞簡化為無限區(qū)域的豎井問題(圖 3)。隧洞地下水水頭H很高，處于穩(wěn)定流，且流線為指向井軸的圓柱面，同時考慮到隧洞的襯砌與注漿圈，假定通過各個過水斷面的流量相等，襯砌滲透力簡化為孔隙水壓力。王建宇(2003)將圓形隧洞近似為軸對稱問題，利用達西定律和豎井理論推導出涌水量的解析公式，表達式為：

(13)

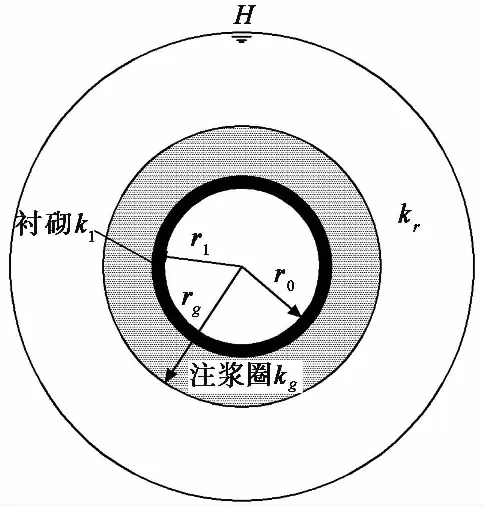
圖 3 豎井法(王建宇， 2003)Fig. 3 Sketch of shaft well method(Wang， 2003)

Maréchal et al. (2003)利用Jacob定降深井流解析解，建立Alpine隧洞變化涌水量模型； 王秀英等(2004)基于王建宇的研究，進一步獲得高水位隧洞注漿圈外水頭的表達式。

Perrochet(2005)在隧洞非穩(wěn)定流涌水問題做出了相關突破，首先利用直接對數(shù)函數(shù)將定降深非穩(wěn)定井流經(jīng)典解析解(Jacob et al.，1952)進行簡化，進一步推導出隧洞涌水量的非穩(wěn)定流解析公式，如下：

(14)

式中，T為導水系數(shù)(m2·d-1)；s0為定降深(m)；S為貯水系數(shù)；r0為隧洞半徑(m)。該公式不足在于實際工程中定降深s0難以確定，且僅僅適用于承壓含水層中隧洞涌水計算。

2.3 保角變換法

保角變換法的實質(zhì)是將笛卡爾坐標系下半無限含水層隧洞問題轉化為復平面極坐標下雙環(huán)問題，從而順利求解出滲流控制方程的通解，再通過逆變換推導出涌水量精確解析解(圖 4)。圖 4中r為隧洞半徑，h為地表面至隧洞中心高度，笛卡爾平面內(nèi)隧洞邊界、地表面、地表面以下任意一點分別轉換為復平面內(nèi)半徑為α、1和ρ的圓。Verruijt(1997)率先將保角變換法應用在隧洞應力-應變問題的求解上，推導出隧洞周圍應變、應力和位移的解析公式，并解決了Mindlin隧洞一系列工程問題。Park et al. (2008)首次利用保角變換法解決隧洞涌水量問題，保角變換的推導過程如下：

(15)

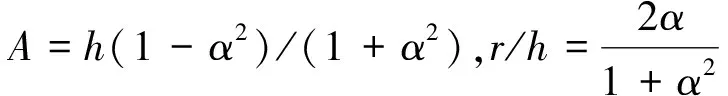
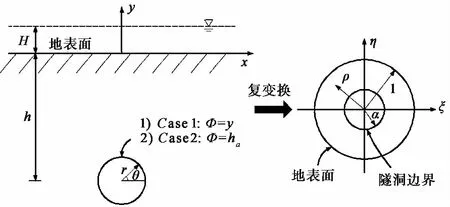
圖 4 保角變換法(Park et al.，2008)Fig. 4 Conformal mapping method(Park et al.，2008)1. 半無限含水層隧洞； 2. 復平面共形映射

將穩(wěn)態(tài)滲流控制方程在復平面ξ-η坐標系轉換為：

(16)

得到通解：

(17)

式中，C1、C2、C3及C4為待定系數(shù)。根據(jù)初始地下水位線邊界條件和兩種隧洞邊界條件(圖 4)：零孔隙水壓力邊界(Case 1)和定水頭邊界(Case 2)，分別得到兩種隧洞邊界條件下涌水量精確解析解，如下：

(18)

(19)

式中，Q1為零孔隙水壓力邊界下隧洞涌水量(m2·d-1)；Q2為定水頭邊界下隧洞涌水量(m2·d-1)；ha為給定的定水頭(m)；H為水位至地表面高度(m)。

Park et al.(2008) 對上述兩種封閉形式的涌水量精確解分別進行討論： ①假定ha=-h和H=0，式(19)簡化為：

(20)

事實上Lei(1999)、Kolymbas et al. (2007)推導出解析公式與式(20)相同。②假定h>>r，式(20)進一步簡化為：

(21)

可知，Goodman推導的解析公式與式(21)相同。

我國學者同樣利用保角變換法在解決隧洞問題上取得了大量的成果，皇甫明等(2009)選擇不同的復變換映射關系式，將隧洞z平面區(qū)域轉化ζ平面矩形區(qū)域(圖 5c)，區(qū)別于雙圓環(huán)區(qū)域，推導出隧洞周圍水頭和孔隙水壓力分布解析公式。

圖 5 保角映射示意圖(皇甫明等， 2009)Fig. 5 Plane of conformal transformation(Huang et al.，2009)

杜朝偉等(2011)針對圍巖、注漿圈和襯砌組成的暗挖水下隧道滲流場，分別利用保角變換法與豎井法推導出圍巖與注漿圈內(nèi)滲流場解析，根據(jù)水流連續(xù)性原則，即兩部分滲流量及注漿圈水壓力相等，得到隧洞涌水量、初次支護和二次襯砌水頭解析式。但是該研究的不足之處在于仍然未能解決豎井法的缺陷，涌水量解析解受限于隧洞埋深限制。

對于考慮襯砌或者注漿圈作用的隧洞，則往往要采用大埋深假定，凡是能夠適用于任意埋深的，又沒有到考慮襯砌或者注漿圈作用。朱成偉等(2017)利用保角變換法解決了上述存在的問題，推導出能夠求解任意埋深下水下襯砌隧洞滲流場涌水量解析解(圖 6)。

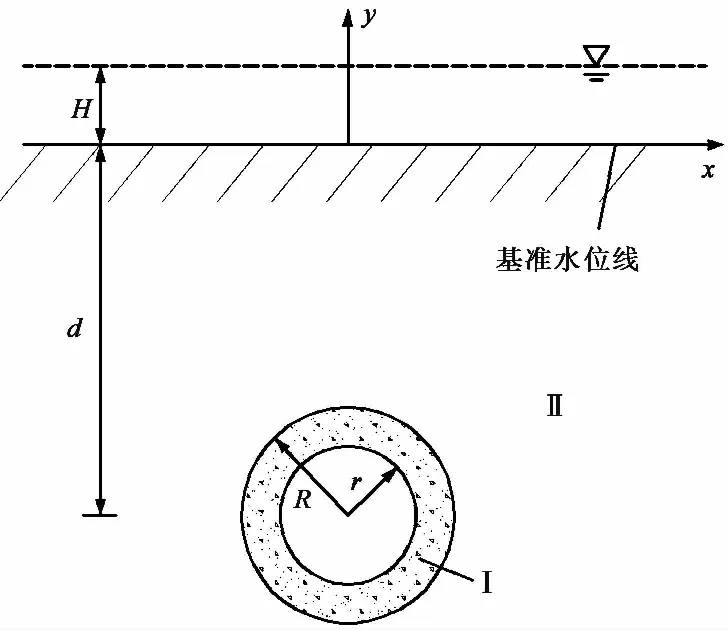
圖 6 水下隧道數(shù)學模型(朱成偉等， 2018)Fig. 6 Schematic diagram of underwater tunnel(Zhu et al.，2018)

2.4 其他解析方法

(22)

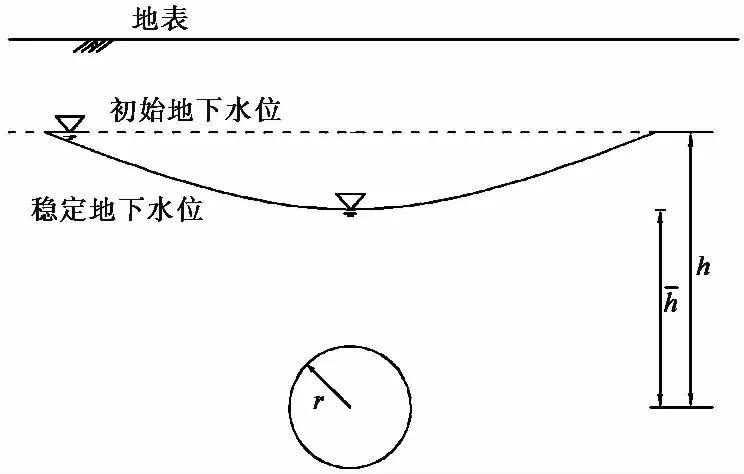
圖 7 隧洞降落地下水位示意圖Fig. 7 Lowered water level of a drained tunnel

蘇凱等(2017)在Moon et al. (2010)研究的基礎上利用有限元軟件ABAQUS，計算出隧洞不同的初始地下水位高度和隧洞半徑下涌水量和降落水位，根據(jù)降落水位數(shù)值計算結果，回歸擬合出降落水位的經(jīng)驗公式，在Goodman公式的基礎上，進一步提出了地下水位下降條件下隧洞涌水量的半解析公式：

(23)

(24)

表 3 隧洞涌水量解析公式Table 3 Analytical equations of water inflow into tunnels

該公式更加有利于工程應用，具有不錯的精度。

針對解析公式的適用范圍問題，EI-Tani(2003)首次指出當隧洞半徑r與地下水位h之比小于0.3時，解析公式計算誤差可以忽略，當r/h大于0.3時，部分解析公式(Goodman公式、Karlsurd公式、Lei公式)計算誤差顯著增大。

還有部分學者根據(jù)裂隙幾何參數(shù)的實測數(shù)據(jù)，回歸擬合出裂隙滲透系數(shù)的經(jīng)驗公式，將經(jīng)驗公式與Goodman公式相結合，進一步提出隧洞涌水量的半解析公式(Gattinoni et al.， 2010； Farhadian H et al.，2016a, 2016b,2016c)，隧洞涌水量解析公式見表 3。

利用解析計算法推導隧洞涌水量公式的核心與難點在于解決地下水位邊界問題，其中鏡像法利用通過實際滲流場與虛擬滲流場的疊加，解決這一邊界問題； 豎井法則默認地下水水頭很高，忽略初始地下水位上邊界與基底下邊界，這造成豎井法計算結果往往偏大，其理論嚴謹性不足。相比較鏡像法與豎井法，保角變換法具有更嚴密的理論推導過程，可以得到更加精確的解析解，使其不受到大埋深的限制； 其他方法則借助多種手段(如數(shù)值計算方法、回歸分析)入手。其次，解析公式普遍存在的問題是其初始假定條件相對簡單，對于非均質(zhì)各向異性介質(zhì)、非達西流及地下水位波動等一些復雜條件仍未得到很好地解決。最后，解析解的準確性十分依賴于參數(shù)的選取，其中最主要是滲透系數(shù)K，大多數(shù)學者采用“等效滲透系數(shù)”來概化分析復雜的圍巖、注漿及襯砌條件下地下水滲流特性，忽略節(jié)理裂隙、地質(zhì)構造、地層分布等控水因素，這顯然是不合理的，同時也是解析計算結果與實際數(shù)據(jù)偏差很大的主要原因，因此如何合理地確定“等效滲透系數(shù)”是一個亟待解決的問題。

表 4 隧洞數(shù)值計算模型Table 4 Numerical calculation models of tunnels

3 數(shù)值計算法

3.1 數(shù)值計算方法

目前，隧洞工程中廣泛應用的數(shù)值計算方法有：有限元法、邊界元法、有限差分法、離散單元法等，其中有限元法(FEM)與有限差分法(FDM)是最為成熟的數(shù)值方法，特別適用于中小尺度下等效連續(xù)介質(zhì)模型(王媛等， 2009； 夏強等， 2010)。離散單元法(DEM)是當前裂隙巖體數(shù)值計算的研究熱點，主要適用于復雜地質(zhì)條件下裂隙網(wǎng)絡模型，它將裂隙巖體視為由離散的巖塊與節(jié)理裂隙組成，裂隙作為滲流運動管道，滲流符合立方定律，巖塊與裂隙之間可以發(fā)生耦合作用(孫玉杰等， 2009)。王貴君(2004)應用離散單元法對節(jié)理裂隙巖體中不同埋深無支護暗挖隧洞的穩(wěn)定性及其機理進行了數(shù)值分析； Fernandez et al. (2010a,2010b)利用離散元軟件UDEC分析了隧洞開挖對裂隙巖體滲透系數(shù)和隧洞涌水量的影響； Farhadian et al. (2016)利用UDEC離散元軟件，結合滲透系數(shù)張量原理，對Karaj輸水隧洞涌水量進行評價，將數(shù)值計算法、經(jīng)驗公式法和實測數(shù)據(jù)進行對比分析，為工程建設提供建議； 謝海文等(2017)對裂隙隧洞中裂隙擴張規(guī)律、滲流場分布特征及涌突水特征進行了研究。

3.2 數(shù)學模型選取

隧洞滲流場的求解，需要結合實際地質(zhì)條件，選取合理的數(shù)學模型。當前數(shù)學模型可分為效連續(xù)介質(zhì)模型、雙重介質(zhì)模型、離散網(wǎng)絡裂隙模型、滲流耦合模型、黑箱模型等，本文對主流的幾種數(shù)學模型進行介紹，詳細見表 4。

(1)等效連續(xù)介質(zhì)模型：當研究區(qū)域尺度較小且存在表征單元體(REV)時，將巖體-裂隙系統(tǒng)等效為連續(xù)介質(zhì)，利用REV體現(xiàn)研究區(qū)內(nèi)巖體和裂隙介質(zhì)的滲流特性(仵彥卿等， 1996； 周志芳， 2004)。

(2)離散網(wǎng)絡裂隙模型：當研究區(qū)巖體內(nèi)大規(guī)模裂隙分布較為稀疏，且?guī)r塊滲透系數(shù)十分低，其REV不存在或大小超過研究區(qū)尺度時，適用于離散網(wǎng)絡裂隙模型(周志芳， 2004)。離散裂隙網(wǎng)絡模型通常假定巖塊本身不透水，地下水通過裂隙網(wǎng)絡運動，且符合立方定律。Farhadian et al. (2016)針對Amirkabir隧洞涌水問題，利用裂隙網(wǎng)絡模型生成大量裂隙，將數(shù)值生成的裂隙與現(xiàn)場實測裂隙數(shù)據(jù)對比驗證，回歸擬合出一種裂隙滲透系數(shù)的經(jīng)驗公式，從而修正了Goodman公式的滲透系數(shù)，提出了一種基于Goodman公式的隧洞涌水量經(jīng)驗公式。

(3)雙重介質(zhì)模型：雙重介質(zhì)模型認為裂隙巖體是巖塊孔隙系統(tǒng)和裂隙系統(tǒng)兩者的相互疊加，其中裂隙導水，巖塊貯水。兩種連續(xù)介質(zhì)中的滲流均滿足達西定律，并依據(jù)兩種介質(zhì)中水交換項來聯(lián)立滲流控制方程(周志芳， 2004)。Huang et al. (2013)利用雙重介質(zhì)耦合模型，研究了惠州抽水蓄能電站引水隧洞涌水量變化規(guī)律。

(4)滲流耦合模型：隧洞開挖擾動巖體原始應力場，造成圍巖損傷，隧洞周圍滲流是應力場、損傷場和滲流場相互作用產(chǎn)生的(劉繼國等， 2006； 周亞峰， 2016； 范勇等， 2017； 李璐等， 2017)。滲流應力耦合效應可分為直接耦合和間接耦合，耦合方式分為線性耦合方法和非線性耦合方法，根據(jù)耦合問題和方式的不同，耦合模型可分為經(jīng)典滲流模型(等效連續(xù)介質(zhì)模型、離散網(wǎng)絡裂隙模型、雙重介質(zhì)模型)與滲流損傷模型(仵彥卿等， 2000； 劉仲秋等， 2008)。陳衛(wèi)忠等(2006)選取滲流耦合模型，通過有限元法模擬山西萬家寨引黃工程高壓出水岔管在運行期圍巖和襯砌中的滲流場特征，分析了岔管中襯砌和圍巖內(nèi)的滲透壓力分布規(guī)律。

表 5 隧洞涌水量預測計算實例分析Table 5 Case study on predicting groundwater inflow into tunnels

3.3 模型范圍、邊界條件及參數(shù)選取

數(shù)值計算的準確性受到模型范圍、邊界條件與材料參數(shù)等因素的影響。在建立模型過程中，若隧洞邊界與模型外部邊界之間距離過小，則隧洞涌水量的計算結果偏大； 反之，若距離過大，數(shù)值計算不僅需要消耗大量時間，而且后處理更加復雜。Butscher(2012)研究了模型范圍對隧洞涌水量的影響； 周亞峰等(2014)從水工隧洞襯砌外水壓力角度出發(fā)，建議模型范圍取距離隧洞中心不小于30倍洞徑(30D)的寬度或高度； Farhadian et al. (2016)采用離散單元法，考慮到裂隙巖體中水力耦合作用，探討了裂隙巖體中隧洞最優(yōu)模型范圍的選取。

根據(jù)實際地質(zhì)條件，模型設定合理的邊界條件(定水頭邊界、隔水邊界及零孔隙水壓力邊界)。此外，鄭宏等(2005)針對水利水電工程中防排水設施，提出了一種新的邊界類型(Signorini邊界)。

4 物理模擬法

物理模擬法包括現(xiàn)場示蹤試驗、水電模擬、室內(nèi)物理模型實驗等，它的核心思想是利用主要室內(nèi)或現(xiàn)場試驗研究隧洞涌水機理，可以直觀地反映出隧洞施工過程中滲流場變化規(guī)律，直接揭露出可能出現(xiàn)的涌水重點部位，為研究區(qū)水文地質(zhì)特征、隧洞富水性分段、涌水量計算提供依據(jù)。但物理模擬法受到現(xiàn)場因素影響較大，存在尺度效應，且試驗具有耗時久、難度大、費用高等缺點(曾亞武等， 2001)。王克忠等(2009)基于室內(nèi)三維物理模型實驗，研究了深埋長大引水隧洞圍巖滲透性變化規(guī)律，為引水隧洞的防滲施工技術設計提供理論依據(jù)； 高飛等(2012)運用水電模擬室內(nèi)實驗方法，研究了各種結構井的滲流機理； 方良成等(2013)采用水電模擬法對淮南礦區(qū)底板灰?guī)r水進行評價，預測礦井災害水源的水量大小； 萬繼偉等(2017)利用現(xiàn)場同位素示蹤試驗探測分析引漢濟渭工程黃三輸水隧洞的水文地質(zhì)條件。

隧洞涌水具有隨機性，復雜性和難以預測等特性，涌水預測計算伴隨著工程勘測設計到施工的整個過程，這需要根據(jù)實際數(shù)據(jù)不斷地反饋修正前期計算結果，從而防止出現(xiàn)計算或模擬失真。表 5是針對國內(nèi)外隧洞涌水實際案例進行總結，列出不同計算方法在實際工程中的應用效果，可以看出數(shù)值法預測結果較為準確，而經(jīng)驗公式與解析公式法的預測計算結果則存在一定的誤差，特別對于裂隙發(fā)育地層。

5 結論與展望

5.1 結 論

隧洞涌水問題一直是實際工程中難以解決的問題，本文基于近年來國內(nèi)外學者在隧洞涌水量預測計算問題上取得的研究成果，分類總結出經(jīng)驗公式法、解析公式法、數(shù)值計算法及物理模擬法4種計算方法，并對各種方法的適用條件及優(yōu)缺點進行了分析，得到如下幾點結論：

(1)經(jīng)驗公式法包括傳統(tǒng)經(jīng)驗公式與現(xiàn)場綜合因素評判方法，這類方法多來源于工程案例的總結，如現(xiàn)場綜合因素評判方法，考慮到現(xiàn)場多種影響因素，運用定性與定量的手段判斷出涌水大致位置與涌水量大致范圍，但其計算結果往往與實測偏差很大。

(2)解析公式法總體上可分為4類：以地下水動力學為基礎的鏡像法與豎井法、保角變換法以及其他解析方法。鏡像法與豎井法理論相對簡單，應用較為廣泛，但受到隧洞大埋深的限制； 保角變換法理論推導過程嚴密，可以求解出任意埋深下隧洞涌水問題，但仍無法解決隧洞地下水位下降條件下涌水問題，其他解析方法主要是一些混合方法，如解析公式與數(shù)值分析方法的結合，但這類方法的理論推導過程不嚴密。

(3)數(shù)值計算方法主要應用復雜水文地質(zhì)條件下隧洞涌水量問題的計算，如有限元法、離散單元法、有限差分法等，這類方法可以很好的模擬實際工程地質(zhì)條件，如地層分布、節(jié)理裂隙及斷層構造等，且計算精度較高，但它的不足之處在于前期地質(zhì)建模需要大量的時間與精力，輸入?yún)?shù)需要較高的精度質(zhì)量。

(4)物理模擬法則借助現(xiàn)場野外試驗或室內(nèi)模型試驗的手段，直觀地顯現(xiàn)隧洞涌水規(guī)律，為研究區(qū)水文地質(zhì)特征、隧洞富水性分段、涌水量計算提供依據(jù)。但物理模擬法受到現(xiàn)場因素影響較大，存在尺度效應，且試驗具有耗時久、難度大、費用高等缺點。

5.2 展 望

盡管當前隧洞涌水問題研究取得了大量的成果，但筆者認為仍有許多問題需要展開更深入的研究：

(1)隧洞的開挖造成地下水位的下降，進一步引發(fā)一系列的環(huán)境影響，地下水位的求解本質(zhì)上是滲流自由面的確定問題。當前關于隧洞滲流自由面的研究較少，隧洞邊界條件設定(定水頭或水壓力邊界)也存在不合理之處，且自由面由數(shù)值方法計算十分不利于工程應用，因此隧洞滲流自由面問題應展開更深入的研究。

(2)當前解析推導過程中主要將隧洞圍巖、襯砌或注漿圈假定為均質(zhì)各向同性介質(zhì)，或其中之一為非均質(zhì)，如Tan et al. (2018)假定隧洞襯砌為非均質(zhì)，介質(zhì)滲透系數(shù)呈線性變化，推導出隧洞涌水量和外水壓力分布解析公式。但實際條件中隧洞圍巖與襯砌一般都是非均質(zhì)各向異性，大部分學者往往采用等效滲透系數(shù)進行簡化處理，因此對于介質(zhì)的非均質(zhì)性各向異性問題，仍需要進一步深入的研究。

(3)多場耦合模型是當前隧洞數(shù)學模型的發(fā)展趨勢，耦合模型可以與多種數(shù)值模型和其他計算方法相互驗證。當前耦合模型主要局限于滲流場、應力場和損傷場的研究，而對溫度場、非達西滲流等方面研究較少(劉仲秋等， 2008； 王媛等， 2012)。此外，耦合算法的參數(shù)敏感性分析、求解效率和精度仍需要進一步加強研究。

(4)從微觀層面上加強對隧洞涌水過程中裂隙幾何參數(shù)變化機理的研究，如節(jié)理裂隙幾何參數(shù)的變化對隧洞圍巖應力重新分布和變形的影響； 襯砌混凝土損傷裂隙的發(fā)育對隧洞涌水、外水壓力分布支護結構的穩(wěn)定性等方面的影響。

(5)隧道涌水量預測計算結果直接指導著下一步防排水措施選擇，圍巖穩(wěn)定性加固，地表沉降變形控制及地下水疏干影響等其他方面，這涉及到給排水、巖土、結構等多個領域(司小東等， 2017)。因此，不可局限于單一的涌水量預測計算，需要更加靈活地將多學科相互交叉，從更寬廣的視野進行研究內(nèi)容的拓展。