基于正交試驗、組合賦權-灰色關聯度法研究隧道施工最優方案*

吳 波，路 明，雷 領，黃 惟，蘭揚斌

(1.廣西大學 土木建筑工程學院，廣西 南寧 530004；2.廣西大學 工程防災與結構安全教育部重點實驗室，廣西 南寧 530004； 3.中交路橋建設有限公司，北京 101116)

0 引言

近些年來，我國城市地鐵快速發展，建設數量和建設里程逐年增加，并取得巨大成就。城市地鐵淺埋暗挖大斷面隧道，因其跨度大，施工工序復雜，對圍巖造成多次擾動，地表沉降難以控制，施工難度大[1]。合理選擇施工方案是隧道順利竣工的前提，針對影響淺埋暗挖大斷面隧道的穩定性因素，調整隧道施工參數，以保證隧道施工過程中的穩定性。

大多學者采用數值模擬、模型試驗、理論研究和現場監測數據等方法研究影響隧道穩定性的因素。來弘鵬等[2]采用現場試驗研究加固區范圍及其參數對隧道穩定性的影響規律；汪波等[3]采用數值模擬和現場試驗等手段研究隧道加固方式和加固參數對砂性土淺埋暗挖隧道的影響；劉泉聲等[4]采用模型試驗和數值模擬手段研究隧道開挖順序對隧道穩定性的影響，從而提出了特大斷面淺埋暗挖隧道十字巖柱開挖技術；黃鑫等[5]采用數值模擬研究隧道埋深、隧道形狀和側壓力系數對隧道施工的影響；吳波等[6-7]基于控制理論和動態規劃原理，以地表沉降作為評價指標研究開挖工序對隧道穩定性的影響規律，但只用地表沉降作為穩定性評價指標，說服力不足；李梓源等[8]建立了由圍巖等級、開挖尺寸等9個指標組成的多因素模型，采用灰色關聯度對隧道穩定性進行評價，但評價指標的計算權重是1/n，意味著每個評價指標一樣重要，并不符合實際情況；李術才等[9]采用熵值法對灰色關聯度進行改進，建立了隧道坍塌風險評估模型，但權重計算時定性分析和定量分析未充分結合，具有一定的局限性。

上述的學者大多研究對象和評價指標單一，權重計算過程中很難符合實際情況。灰色關聯度法評價指標權重為1/n，意味著各評價指標同樣重要；熵值法—灰色關聯度法在樣本較少，且各樣本差距不明顯時，熵值法的各評價指標權重無明顯差異，具有一定的局限性。

本文根據影響隧道穩定性的因素，構建L16(5×4)正交表進行正交試驗，把地表沉降、圍巖應力、右側導洞拱頂沉降、初支剪應力作為評判指標，用熵值法[10]和層次分析法[11]進行組合賦權，將定性分析和定量分析有效結合，增強其準確性和客觀性，特別在樣本數量和差距均較小時，更能凸顯各樣本的優劣，從而選擇最優方案。

1 組合賦權-灰色關聯度評價法

1.1 灰色關聯度分析法

灰色關聯度分析法[12-13]是將研究對象及影響因素的因子值視為1條線上的點，與待識別對象及影響因素的因子值所繪制的曲線比較它們之間的貼近度，計算研究對象與待識別對象各影響因素之間的貼近程度的關聯度，通過比較各關聯度的大小來判斷待識別對象對研究對象的影響程度。

1)評價指標矩陣

按照灰色關聯度分析法，假設評價系統中有m個評價指標，n個試驗方案，則評價指標矩陣A為：

(1)

2)對指標矩陣歸一化

在系統的各評價指標中，采用越小越優的指標，對指標矩陣進行歸一化，見式(2)：

(2)

式中：rij為特征矩陣R的特征向量，i=1,2,…,n；j=1,2,…,m。

根據式(2)處理后，矩陣A變為：

(3)

3)關聯系數矩陣計算

各指標中的最大值作為參考方案，參考方案矩陣為：K=[k1k2…km]，其中kj=max(r1j,r2j,…,rnj)，j=1,2,…,m。

(4)

其中:

(5)

(6)

式(4)中分辨系數ρ∈[0,1]，本文中取0.5，經過式(4)～(6)處理后得到關聯系數矩陣ζ：

(7)

1.2 組合賦權方法

權重賦值的方法一般有2種：主觀賦權法和客觀賦權法。客觀賦權法采用熵值法，在信息論中，某項指標攜帶的信息量越大，說明該項指標對方案的決策作用越大，所以熵值法是通過計算各項指標值的變異程度來計算權重的。

1)熵值法

對指標矩陣A進行歸一化處理:

(8)

各指標的信息熵：

(9)

熵值法權重：

(10)

2)主觀賦值法

本文采用層次分析法計算主觀權重βj，是指將與決策總是有關的元素分解成目標、準則、方案等層次，在此基礎之上進行定性和定量分析的決策方法。結果的影響程度都是量化的，清晰明確。

3)組合權重

本文將按照文獻[14]中的組合權重進行計算，具體如式(11)所示：

(11)

4)理想方案的關聯度計算

γ=ζω

(12)

式中：ω為組合權系數矩陣；γ為目標函數關聯度矩陣。

2 工程實例

本文依托北京地鐵17號線天通苑站歇甲村出入段線南肢項目，礦山法暗挖隧道里程為RDKO+138～RDKO+421，暗挖長度283 m(單洞雙線283 m，分線樁號為RDK0+421)，隧道平面示意圖如圖1所示。

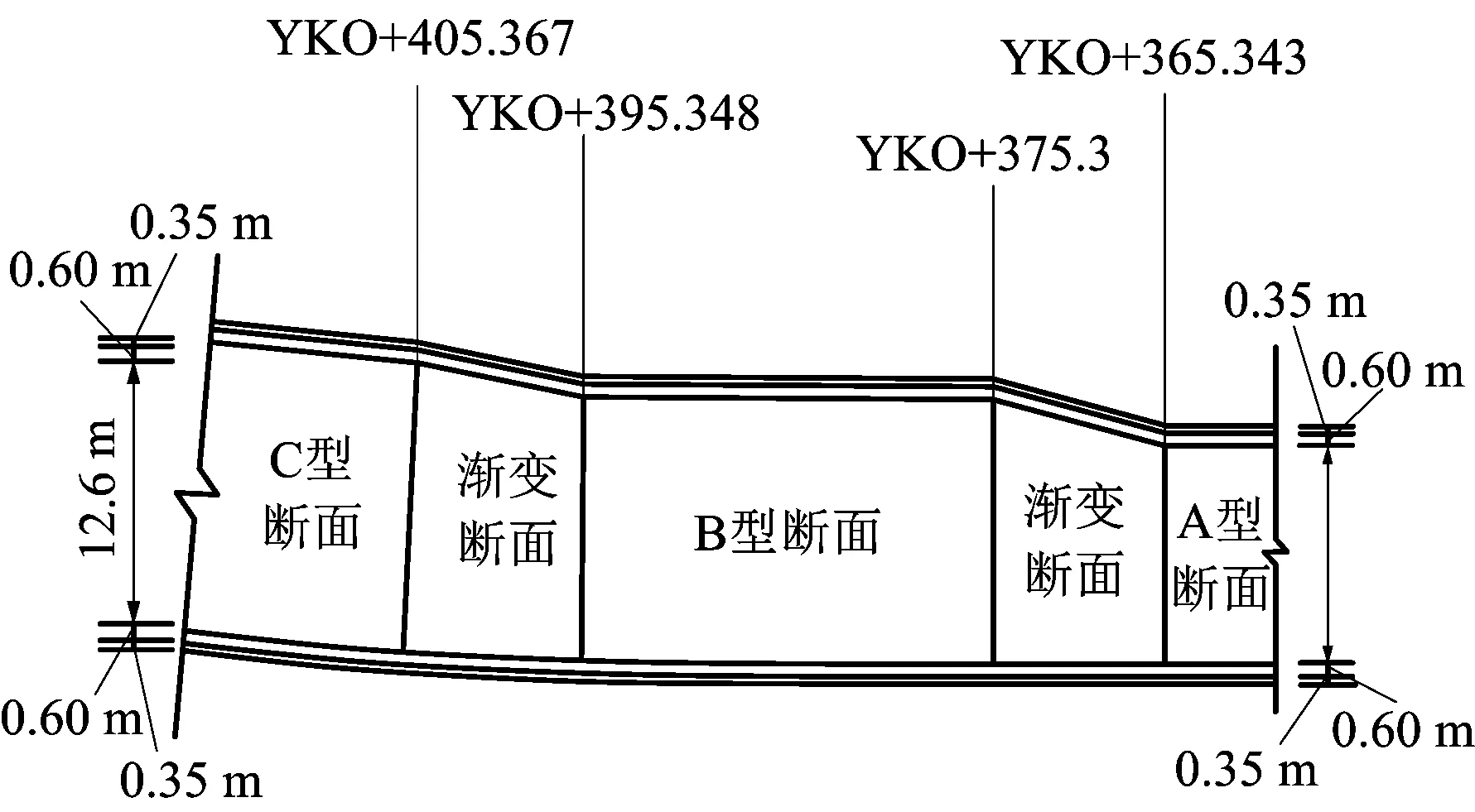
圖1 漸變隧道平面示意Fig.1 Plane plan of gradient tunnel

本文原始方案采用動態分區法(Dynamic partition method簡稱DPM)，將隧道分為2個部分，Ⅰ為固定分區部分，隧道跨度固定為10 m，固定分區分為4個小導洞，分別為Ⅰ-1，Ⅰ-2,Ⅰ-3,Ⅰ-4部，采用CRD工法施工；Ⅱ為動態分區部分，能隨隧道輪廓線增大而增大，從而實現隧道漸變。為了滿足本工程的需求，i最大為4.5 m，最小為2.3 m，動態分區分為2個小導洞，分別為Ⅱ-5，Ⅱ-6部，采用臺階法施工。但是Ⅰ，Ⅱ部之間錯開距離仍需討論。DPM動態分區如圖2～3所示。

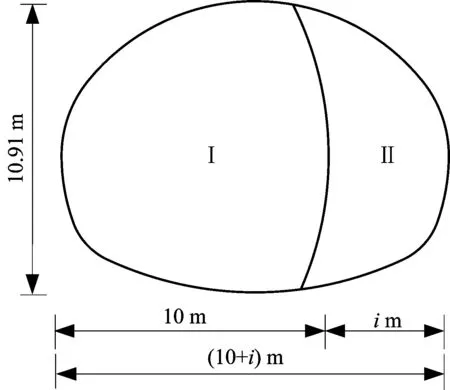
圖2 動態分區法示意Fig.2 Schematic diagram of dynamic partitioning method

2.1 原始方案數值模型計算

對北京地鐵17號線漸變大隧道原始方案進行數值分析，選取歇甲村出入段線南肢暗挖隧道斷面面積最大的C段，跨度為14.5 m，高為10.91 m，埋深為7.5 m。圍巖級別為Ⅵ級，模型X方向120 m，Y方向60 m，Z方向47 m，數值模型見圖3。

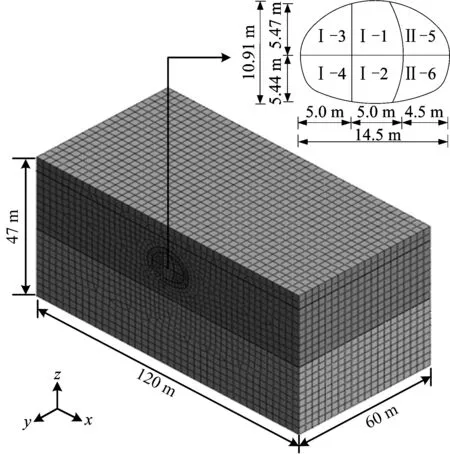
圖3 數值計算模型Fig.3 numerical calculation model

圍巖采用實體單元模擬，初期支護采用植入式梁單元模擬，通過提高加固區圍巖的參數來模擬超前支護作用。根據新奧法的原理，二次襯砌作為安全儲備，因此模型不考慮二次襯砌的影響，材料參數見表1。

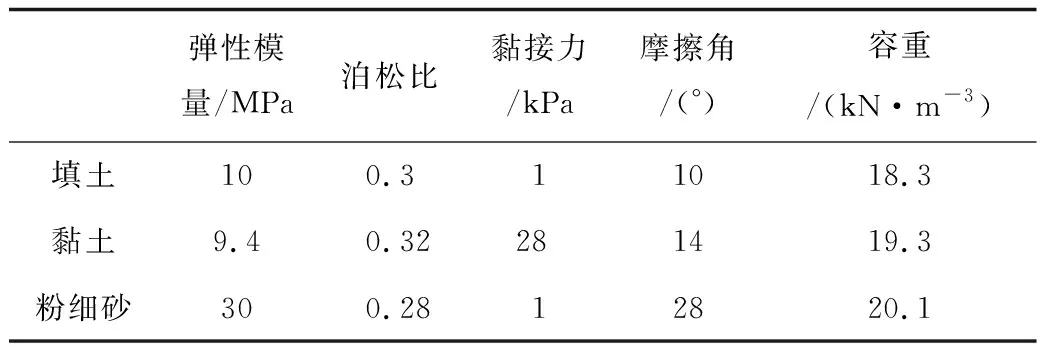
表1 材料參數Table 1 Parameters of materials

原始方案結果如表2所示，但施工步距、加固區強度及范圍Ⅰ,Ⅱ部導洞錯開距離以及施工工序是否是本工程的最優方案，是本文的重點研究內容。

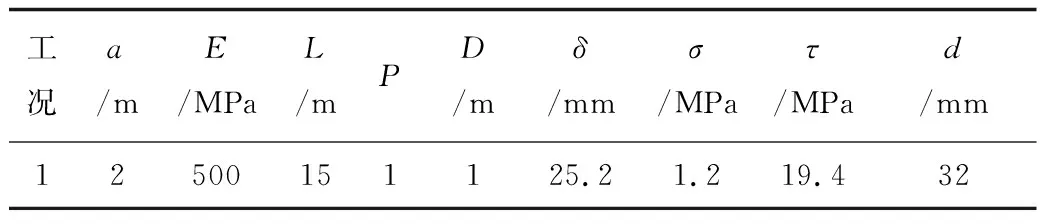
表2 隧道原始施工方案與結果Table 2 Original construction scheme and results of tunnel

注：a為施工步距;E為加固區強度;L為Ⅰ,Ⅱ部導洞錯開距離;P為施工工序;D為加固區范圍;δ為最大地表沉降;σ為圍巖最大應力;τ為初支剪應力;d為右側導洞拱頂沉降。

從文獻[2-3]可知隧道加固范圍和參數對隧道穩定性影響較大，本文隧道加固方式采用全斷面灌漿加固，故將隧道全斷面加固區的范圍和參數為試驗因素；從文獻[6-8]可知隧道施工工序對隧道的穩定性影響很大，因此隧道施工工序是設計因素之一；施工步距影響初支是否能快速封閉成環，故把施工步距作為設計因素之一。施工工序不同即導致的施工順序不同，施工工序如下：P1：1-2-3-4-5-6；P2：3-4-1-2-5-6；P3：5-6-1-2-3-4；P4：5-6-3-4-1-2。

2.2正交試驗設計

在同一埋深和地質條件下，影響城市地鐵淺埋暗挖大斷面漸變隧道穩定性因素較多，本文通過廣泛調研，認為施工工序、施工步距、加固區范圍、強度以及Ⅰ，Ⅱ部導洞錯開的距離等都能影響暗挖隧道穩定性，因此設計L16(5×4)正交表進行正交試驗設計[15-16]，見表3。

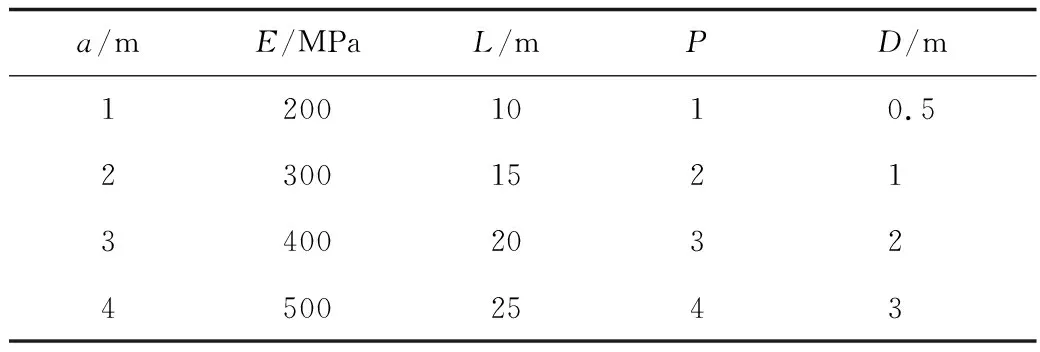
表3 主要影響因素及水平Table 3 Main Influencing Factors and Levels

2.3 試驗方案與結果

表4 為正交試驗方案和結果。由表4可知，工況2的地表沉降最小為22.9 mm；工況1的圍巖應力最小為0.78 MPa；工況1的噴混剪應力最小為6.6 MPa；工況5的右側拱頂沉降最小為27.4 mm。P1和P2的整體結果均偏小，加固區范圍0.5 m和強度500 MPa的計算結果均偏大。

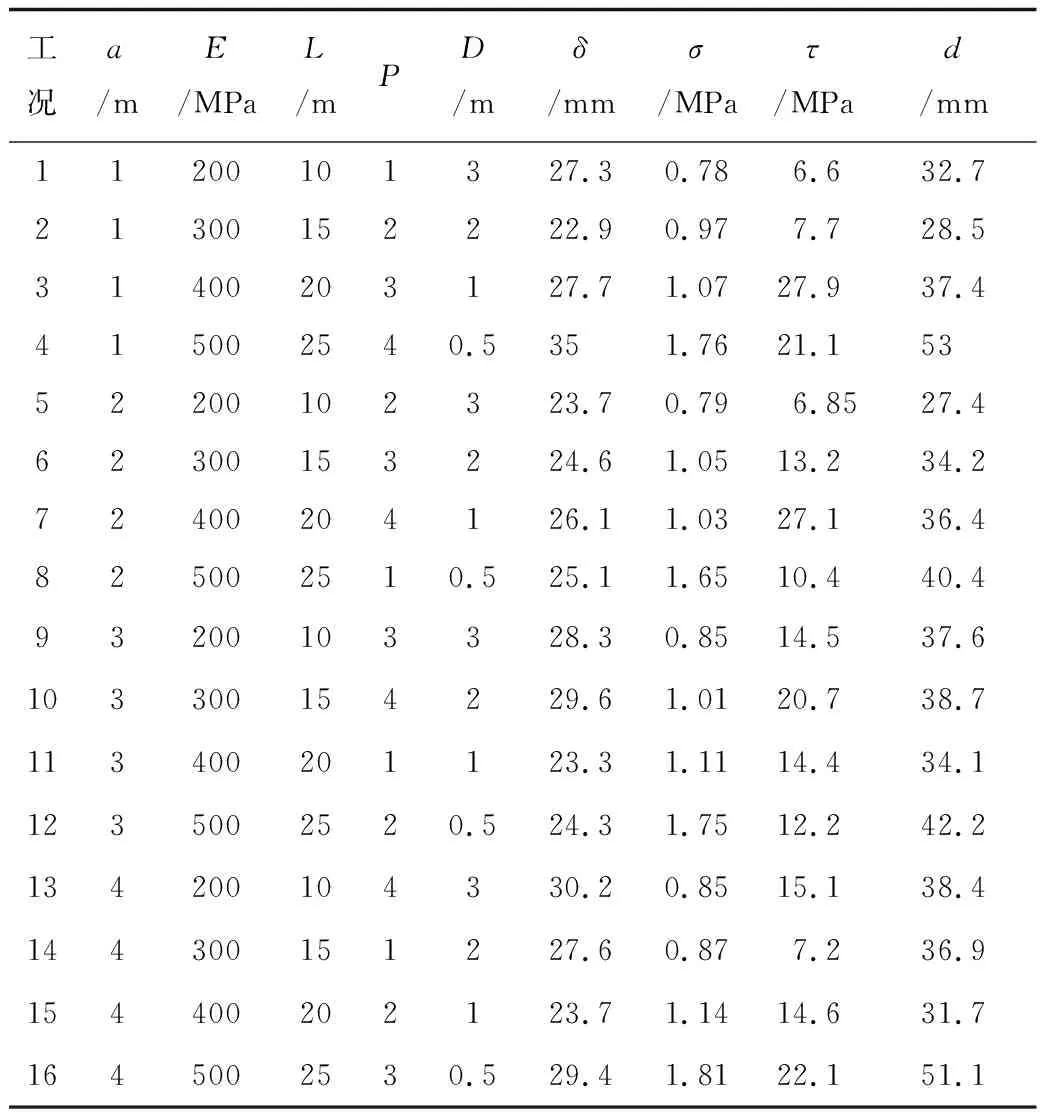
表4 正交試驗方案和結果Table 4 Orthogonal test protocol and results

2.4 數據處理

利用表4中的計算結果構建評價矩陣，再通過式(2)進行歸一化處理，形成特征矩陣R：

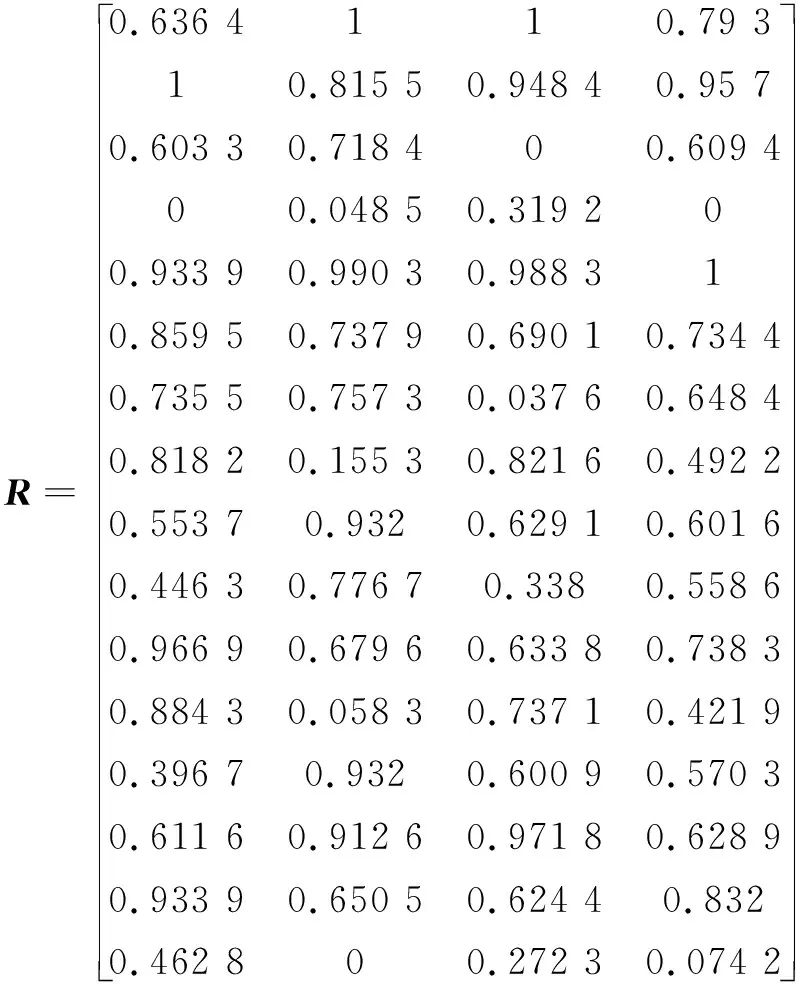
將矩陣R帶入式(4)～(7)可計算出灰色關聯系數矩陣ζ：

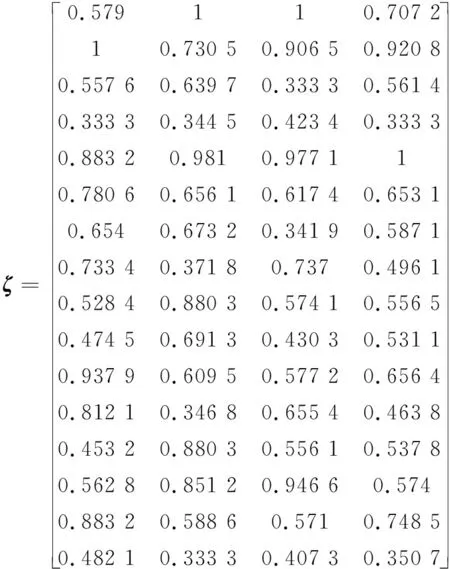
根據式(8)～(10)求得熵值法客觀權重：

αj=[0.256 4 0.249 4 0.239 5 0.254 7]

主觀權重：

βj=[0.213 0.226 0184 0.377]

按(11)式計算組合權重：

ωj=[0.217 5 0.224 4 0.175 5 0.382 6]

經組合賦權后，各指標權重大小依次為：右側拱頂沉降>圍巖應力>地表沉降>初支剪應力。由式(12)計算目標函數的灰色關聯度(見表5)，關聯度越大，方案越好，隧道穩定性越高。由表5可知 ：工況5的關聯度為0.966 3，說明正交試驗中工況5的方案為最優方案，其次是工況2，關聯度為0.892 8。工況16的關聯度為0.385 3，是本次試驗中關聯度最低值的組合，故工況16是最差的方案，隧道穩定性也最差。

其中各水平的平均關聯度如表6所示。施工工序2的平均關聯度最高為0.753 3，說明隧道施工工序2是施工工序中的最優選項。其次“加固區厚度3 m和強度200 MPa”的平均關聯度較高為0.777 6，說明該組合是加固方式和范圍的最優選項。“Ⅰ，Ⅱ部導洞錯開距離、加固區范圍和強度”平均關聯度的極差為0.348 2，故可知其對隧道穩定性影響最大；施工工序平均關聯度的極差為0.223，可知其對隧道穩定性影響較大；施工步距平均關聯度的極差為0.096 6，故可知對隧道穩定性影響最小。從表6可知，平均關聯度越高，說明該項指標越好，故最優方案為：加固區厚度為3 m，強度為200 MPa，施工步距為2 m，Ⅰ，Ⅱ部導洞錯開距離為10 m，施工工序2。最優方案恰好為表5中的工況5，其關聯度為0.966 3。

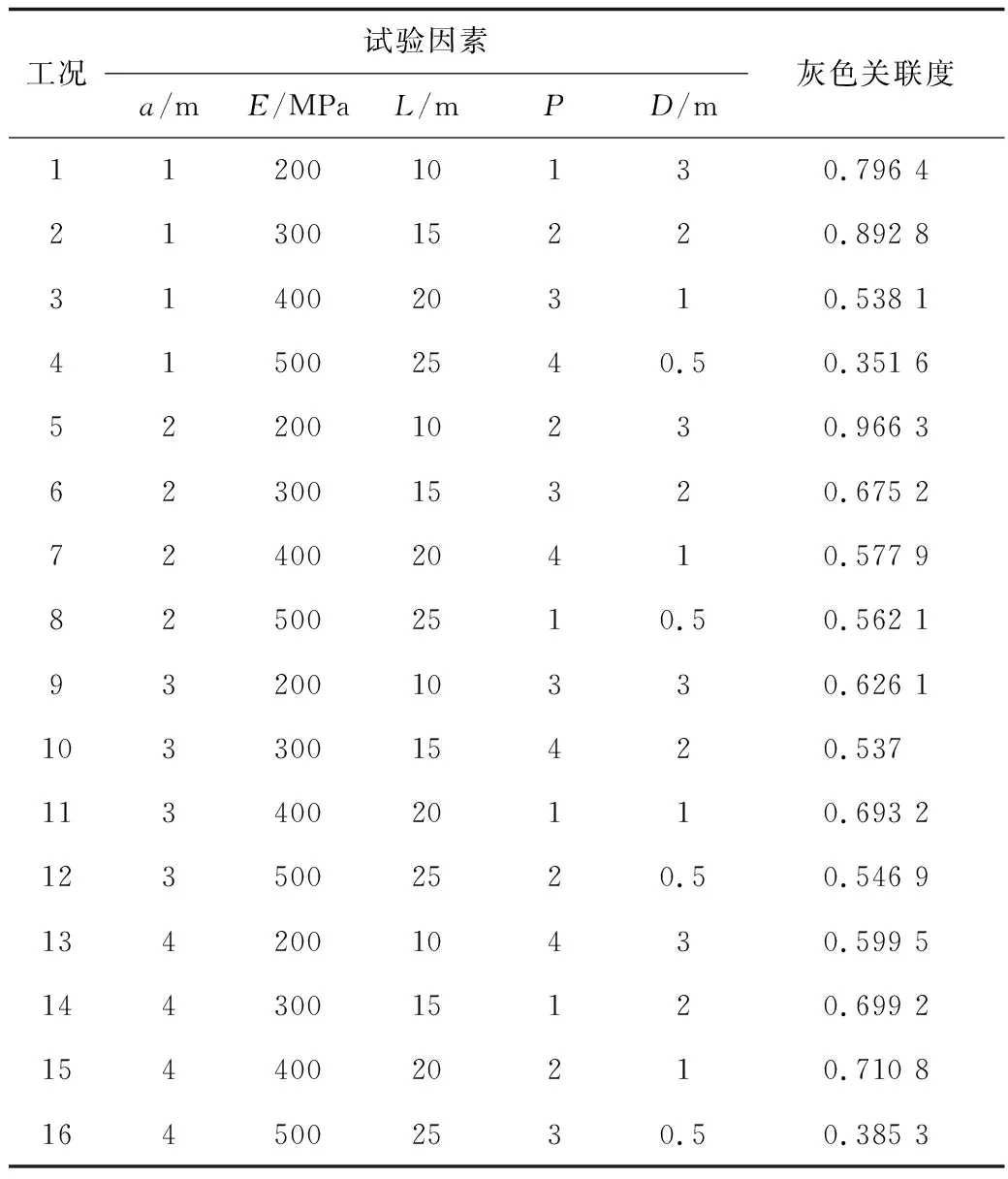
表5 目標函數的灰色關聯度Table 5 Grey correlation degree of objective function

3 優化設計與結果分析

3.1 優化設計

將最優施工方案組合與原始設計組合“步距為2 m，加固區強度為500 MPa，Ⅰ,Ⅱ部導洞錯開距離為15 m，施工工序1，加固區厚度為1 m。”優化前后有限元結果對比分析結果如表7所示。最優方案在各方面結果均比原始設計小，因此隧道整體受力得以顯著改善，隧道穩定性更好。尤其最優方案的剪應力比原始方案小12.55 Mpa，確保噴混不會發生剪切破壞。地表沉降和右側導洞拱頂沉降變形均小于30 mm，滿足地鐵施工規范要求。

表6 各水平平均關聯度Table 6 Average correlation degree of each level

表7 優化前后有限元結果對比分析Table 7 Comparative analysis of finite element results before and after optimization

3.2 多種分析法的結果比較

為了進一步說明本文采用方法的準確性與先進性，另外采取2種方法對隧道的數據進行處理，由于篇幅原因，各方法不做具體說明。其中方法1采用傳統灰色關聯度法，計算權重為1/n；方法2采用熵值法—灰色關聯度計算，方案3為本文方法。各方法的灰色關聯度計算結果如圖4所示。

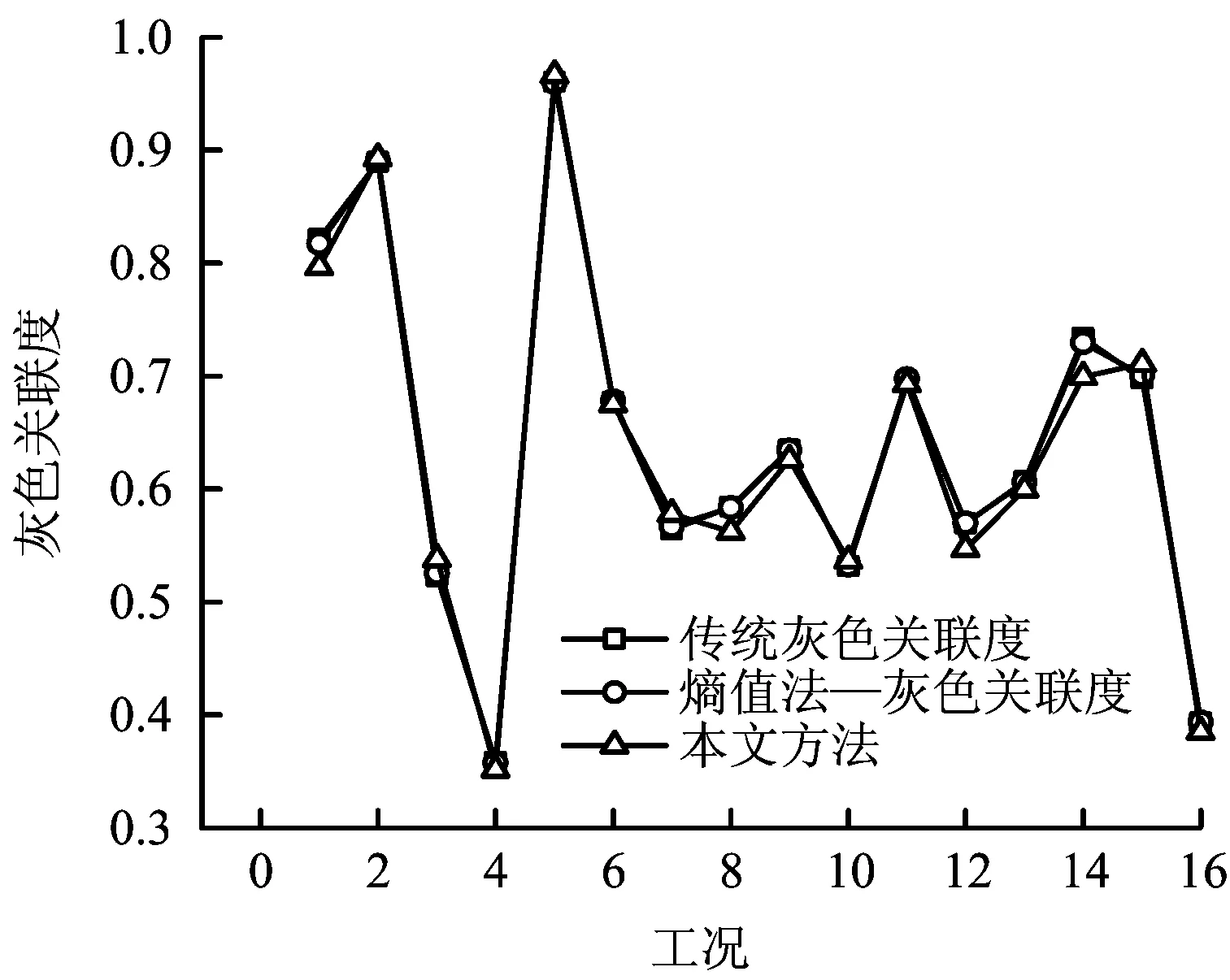
圖4 各種方法對比分析Fig.4 Comparative analysis of various methods

從圖4可知：3種方法計算的關聯度大小無明顯差異，方法3最大灰色關聯度為0.966 3，而方法1最大灰色關聯度為0.960 3，方法2的灰色關聯度為0.959 8，三者差距甚小，而且最優方案均為方案5，驗證了本文方法的準確性。從圖4中可知方法1和方法2幾乎沒有差別，因為熵值法計算各評價指標的權重大致相同，和方法1的權重系數1/n計算結果大致相同。但是方法1傳統灰色關聯度默認所有指標權重相同，導致精確度不高，只能粗略的得出最優方案，當各方案差距較小時，會出現灰色關聯度相同的方案，難以抉擇，方法2與方法1類似。

本文方法將熵值法和層次分析法進行結合，形成組合賦權，將定性分析和定量分析有效結合計算權重，且通過圖4驗證其準確性。本文方法在評價指標類型和數據較多時更為適用，特別是在各方案差距較小時，很少出現灰色關聯度相同的方案，更容易凸顯最優方案，這也是本方法的先進性。

3.3 施工沉降分析

北京地鐵17號線天通苑站采用本文最優方案5施工，固定分區Ⅰ部平均每天掘進1 m，待固定分區Ⅰ部掘進10 m后，開始施工動態分區Ⅱ部，動態分區Ⅱ部每天掘進1.5 m。

施工地表沉降監測數據如圖5所示。施工監測最大地表沉降為-23.2 mm，比模擬結果大10.8%，因為施工現場經常出現鋼拱架支撐不及時；鋼拱架未快速封閉成環等因素，造成施工結果偏大。

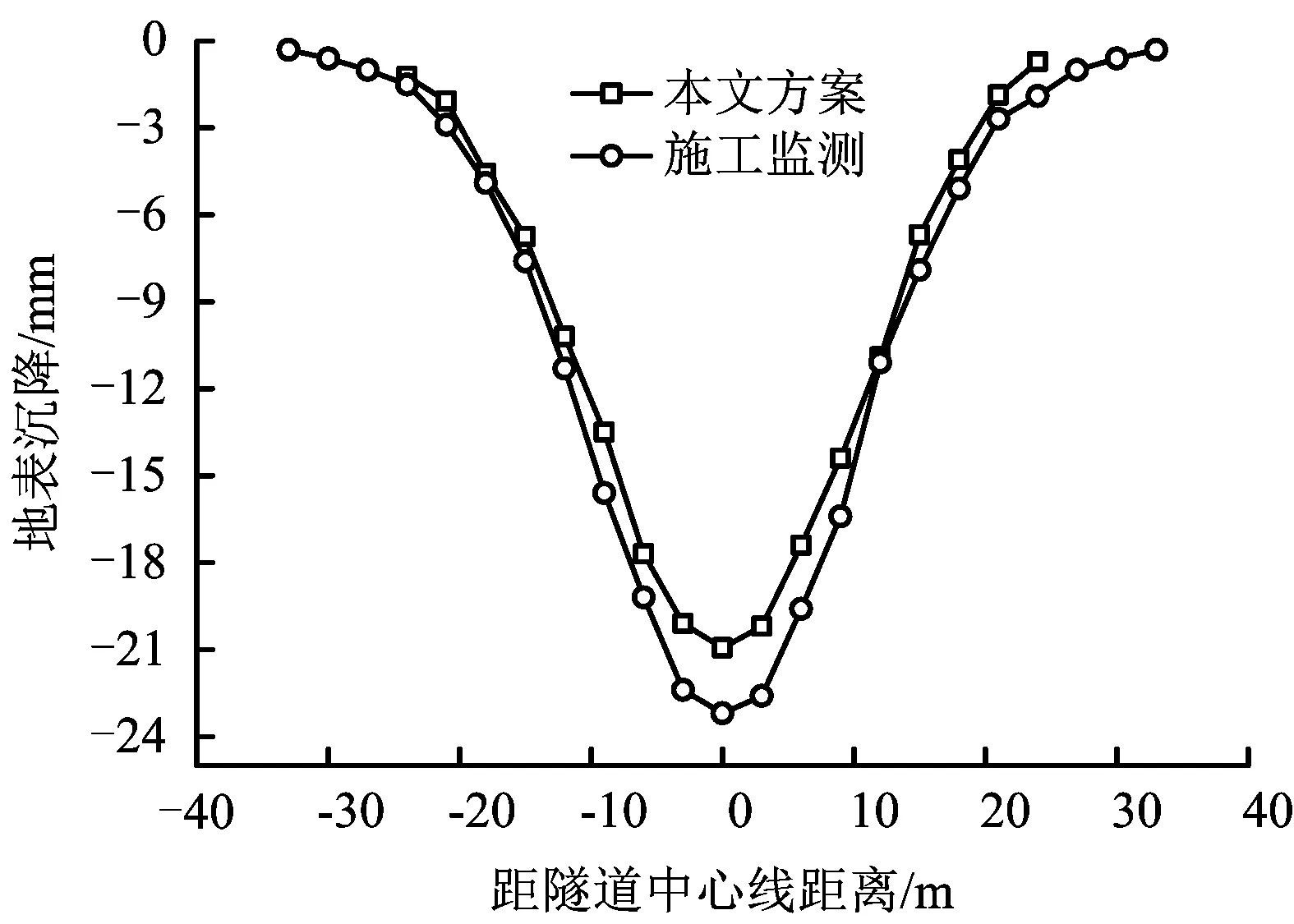
圖5 數值模擬和施工監測地表沉降對比Fig.5 Comparison of ground settlement of numerical simulation and construction monitoring

4 結論

1)采用的正交試驗、組合賦權-灰色關聯度方法研究淺埋暗挖大斷面隧道穩定性的影響因素，從平均關聯度可知：隧道施工工序、加固區強度和范圍、Ⅰ，Ⅱ部導洞錯開距離對隧道整體穩定性的影響較大，施工步距對隧道整體穩定性的影響較小。

2)本文方法選擇出最優施工方案的各項數據均優于原始方案；且與其他2種方法對比分析驗證了本方法的準確性，特別在樣本數量和差距均較小時，更能凸顯各樣本的優劣。

3)組合權重通過熵值法對數據進行客觀處理，更加真實可靠，再通過層次分析法對數據進行主觀評判，增強其邏輯性，最后得出的權重更加真實可靠。因此本文方法選擇隧道施工方案是更加合理的。

4)在復雜環境條件下，合理選擇施工方案，不僅能增強隧道穩定性，保證隧道順利施工，而且能節約成本和時間，為項目帶來巨大的經濟效益和社會效益。本文方法能在短時間內準確的選出最優施工方案，并通過實際工程驗證本方法的先進性，故本方法也能為其他復雜工程方案比選提供借鑒意義。