爆炸荷載下地鐵隧道損傷規律研究

趙 敏，周子豪

(西安工業大學 建筑工程學院，陜西 西安 710021)

0 引言

地鐵給人們生活帶來極大方便，但地鐵在運營中存在諸多風險，其中地鐵淺埋隧道受爆炸威脅是其風險之一。爆炸引起瞬時高強度沖擊荷載可能造成隧道結構失穩破壞，會危及人們的生命財產安全，帶來極大的社會負面影響[1-2]。

目前國內外專家學者對爆炸荷載下地鐵隧道的動力響應規律及損傷規律做了大量分析研究；Ting[3]利用響應振動速度建立了圓形隧道圍巖爆破振動安全準則，結合具體工程實例，分析了隧道的頻率和半徑對隧道的影響；Anirban等[4]采用物理模型試驗和數值分析相結合的方法研究了爆炸效應，發現改變隧道的土壤覆蓋層時，隧道頂部環向應變低于兩側幫；范鵬賢等[5]利用矩陣力法分析爆炸波入射角度對結構動力響應的影響。發現爆炸波入射角度由0°到90°增加時，拱頂位移由向上逐漸變為向下；陳成振等[6-7]研究襯砌與飽和土體相對剛度的影響機理，發現內爆炸下襯砌結構的應力與相對剛度成反比；肖望等[8]對比直隧道、直角彎道、岔口面對沖擊波的動力響應情況，發現沖擊波經過直角彎道和岔口時，沖擊波對襯砌結構的破壞能力被大幅削弱。

爆源位于隧道結構內部的研究方法和理論數據已較為完備，能夠綜合分析多種因素對襯砌結構損傷的影響[9]；反觀爆源位于地面時結構的損傷問題，可以發現考慮的影響因素較為單一[10-11]，且一般認為爆源恰好位于隧道結構正上方，這與實際情況并不相符。鑒于此本文首先以爆源與隧道中心所呈角度為變量，通過對比不同地面側爆角度下結構的損傷程度，進一步分析在側爆角度不變時，增加隧道埋深后隧道上覆土層變化對襯砌結構損傷的影響。此外，本文在應用ANSYS/LS-DYNA軟件進行有限元數值模擬時，充分考慮了爆炸沖擊波經過不同土層介質的衰減效應[12-14]，盡可能與實際情況相符，以期為地鐵隧道的防爆支護提供參考。

1 建立有限元模型

本文所建的有限元計算模型中，隧道襯砌結構外徑為6.1 m，內徑為5.4 m，襯砌厚度為350 mm。計算模型尺寸取為隧道內徑的5倍左右，即取模型高度與寬度均為28 m，厚度為18 m，具體有限元網格見圖1，炸藥包采用立方體TNT進行模擬，如300 kg TNT炸藥的尺寸取560 mm×560 mm×560 mm，采用*MAT_HIGH_EXPLOSIVE_BURN進行炸藥參數的賦值[15]，TNT炸藥包與隧道結構的相對位置如圖1所示。同時所有單元均選擇為3DSOLID164，單元數為43 190；通過對關鍵字段的修改，將側面及底面設置為無反射邊界條件，頂面為自由面，襯砌結構與土體為自由接觸。所建模型共有3種土層，土體均定義為D-P模型，各土層的材料參數見表1。本文所用其他有限元模型僅在此模型基礎上調整即可，為滿足均質性，隧道結構均位于第2層土體，此外不考慮初始應力的作用。

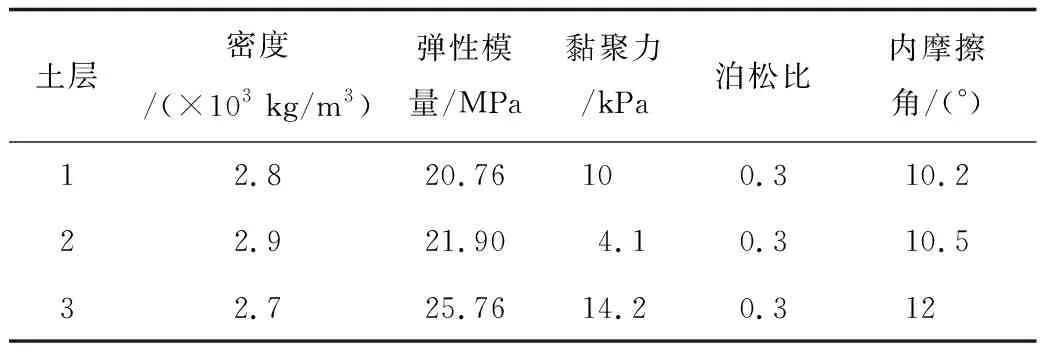
表1 土體動力參數Table 1 Dynamic parameters of soil

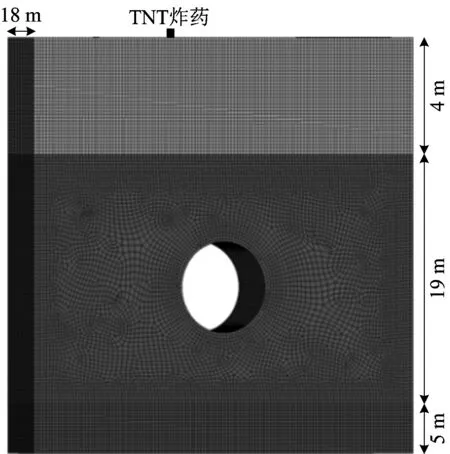
圖1 有限元網格劃分示意Fig.1 Schematic diagram of finite element meshing

利用LS-DYNA軟件，繪制出側爆15°工況與0°頂爆工況下地鐵隧道襯砌結構的最大主應變時程曲線及損傷壓力云圖，對比分析各工況下的時程曲線，同時對動力反應最大的側爆工況建立不同隧道埋置深度的有限元模型做進一步計算分析，用于損傷判定的觀測部位具體部位如圖2所示。

圖2 動力響應觀測部位示意Fig.2 Schematic diagram of dynamic response observation positions

2 不同側爆角度支護結構的動力響應規律

分析地面側爆時側爆角度的選取對襯砌結構損傷破壞，具體設置的工況如表2所示。通過特殊部位節點的主應變時程曲線，并通過時間步為4 000 μs時襯砌結構的壓力損傷云圖(單位：×1011Pa)來分析襯砌結構的損傷特性，損傷云圖如圖3～5所示。

對壓力損傷云圖3進行分析，可以看出，工況1(t=4 000 μs時)襯砌結構損傷范圍是介于拱頂與左側幫之間的部位，且拱頂與左側幫也各有損傷；此外拱底有微弱的損傷破壞，損傷最大的位置位于靠近拱頂的部位。

表2 隧道襯砌結構損傷形態分析選取工況Table 2 Selection of working conditions for damage morphology analysis of tunnel lining structure

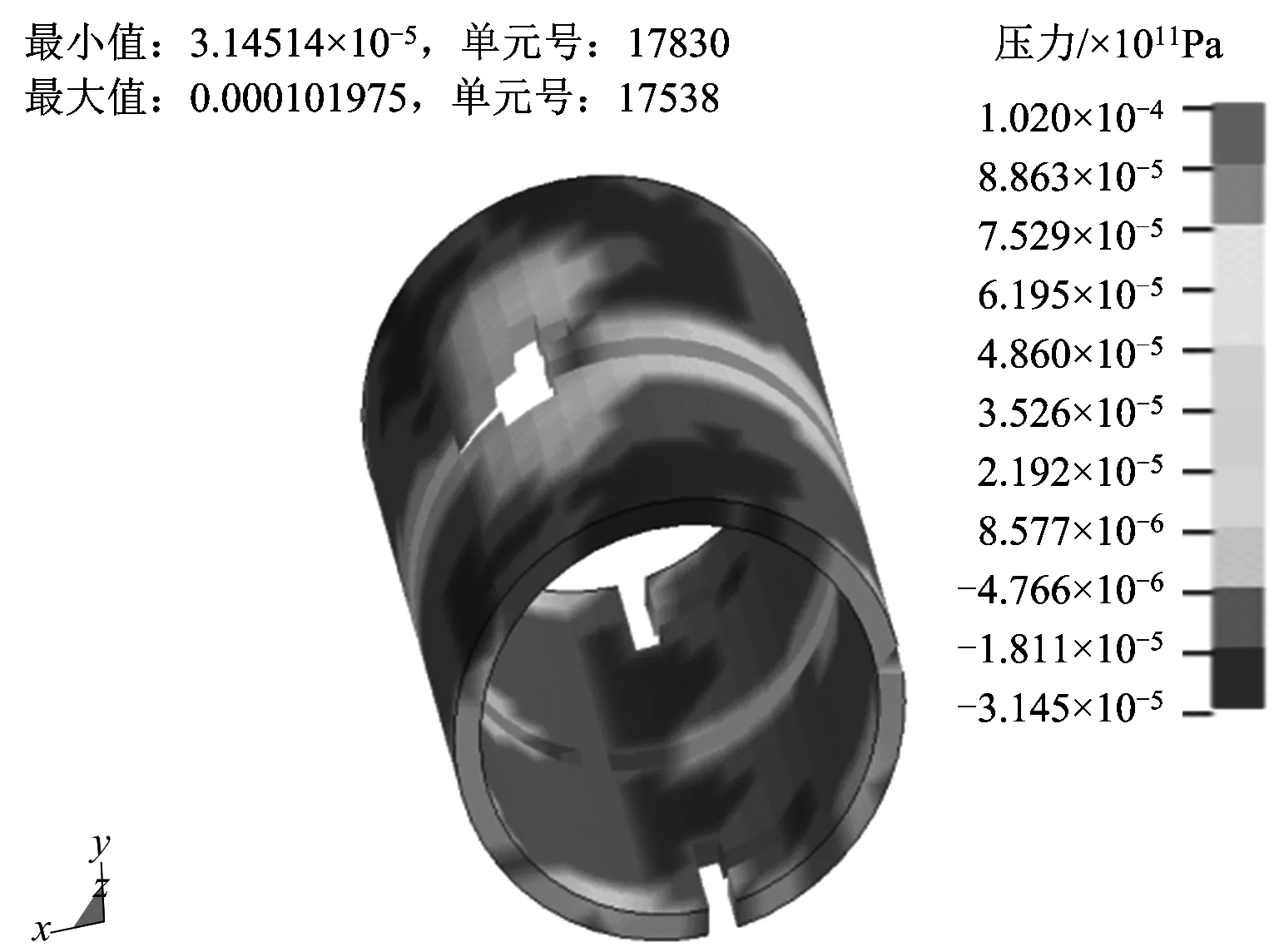
圖3 工況1壓力損傷Fig.3 Pressure damage for working conditions 1

圖4 工況2壓力損傷Fig.4 Pressure damage for working conditions 2

圖5 工況3壓力損傷Fig.5 Pressure damage for working conditions 3

通過工況2(t=4 000 μs時)的損傷云圖，可以看出，損傷范圍有所減小，對比工況1和工況2可以看出，明顯的觀察到工況2損傷的位置有了明顯的下移，偏移效果向下偏移，且拉應變最大的部位也不再是拱頂部位，左側幫上側成為破壞損傷最為嚴重的部位。

進一步通過壓力云圖5，發現襯砌結構在t=4 000 μs時未發生損傷，且各個單元節點的爆炸應力波能量也都極小；綜合對比工況1～3，可以得出，爆炸距離決定著應力波總能量的大小，而襯砌結構的橫向損傷程度則由側爆角度與爆炸距離共同制約，其中側爆角度為15°時，襯砌結構的徑向及橫向均有較大程度的損傷破壞。

3 不同隧道埋深支護結構的動力響應規律

考慮地面側爆時隧道結構位于不同埋置深度對襯砌結構的損傷破壞形態影響，具體設置的工況如表3所示。通過特殊部位節點的主應變時程曲線及2 000，4 000 μs時襯砌結構承受的最大壓力(單位：×1011Pa)來分析襯砌結構的損傷特性，最大主應變時程折線圖及壓力損傷云圖如圖6～11所示。

表3 隧道襯砌結構損傷形態分析選取工況Table 3 Selection of working conditions for damage morphology analysis of tunnel lining structure

工況1的最大主應變時程折線圖及數據的分析如圖6所示。

圖6 工況1最大主應變Fig.6 Maximum principal strain of working conditions 1

由工況1的襯砌結構最大主應變圖可知，隧道埋置深度為12 m時，拱頂處的最大主應變的峰值達到195個拉應變，遠超出拱底的120個拉應變，與左側幫上側的180拉應變較為接近；通過圖6還可看出拱頂、左側幫上及拱底這3個部位最大主應變的最大值較大，可能致使襯砌結構局部出現損傷破壞；同時，左側幫下側部位的最大主應變的峰值并不大，是否出現損傷破壞仍需要進一步分析其損傷云圖。

t=2 000，t=4 000 μs 2個時間步具體的損傷破壞程度如圖7所示。

圖7 隧道埋深12 m時襯砌結構的損傷Fig.7 Lining structure damage for buried depth of tunnel as 12 m

通過應力損傷圖7可以看出，隧道埋深為12 m，t=2 000 μs時表層已出現大面積受損，其中拱頂及側部受損嚴重，拱底出現輕微的損傷；t=4 000 μs時，失效單元有所增加，但發生損傷的位置仍為拱頂及兩側幫，同時可以看出，側部的損傷非常顯著；由此得出，雖然側爆的爆炸距離更遠，但其引起的橫向損傷效應絕不可忽視。

工況2的最大主應變時程折線圖及數據的分析如圖8所示。

圖8 工況2最大主應變Fig.8 Maximum principal strain of working conditions 2

由工況2的襯砌結構最大主應變圖可知，隧道埋置深度為15 m時，觀測部位的對比情況與工況1相似，不同的是，隨著隧道埋置深度的增加，主應變最大值有明顯的衰減，主應變最大值位于拱頂處為175個微應變；左側幫上側部位的最大主應變最大值為150個微應變，是拱頂的86%，拱底的最大主應變最大值為110個拉應變，可能出現局部的損傷破壞。

埋深15 m時地鐵盾構隧道的襯砌結構壓力損傷云圖如圖9所示。

圖9 隧道埋深15 m時襯砌結構的損傷Fig.9 Lining structure damage for buried depth of tunnel as 15 m

分析圖9所示埋深15 m這一工況，t=2 000 μs時，拱頂及左側幫上側均出現輕微損傷，附近單元的爆炸應力波強度較其他部位也更大；t=4 000 μs時，損傷面積有了顯著的增大，但可以看出相較工況1，拱底并沒有出現破壞。同時，對比工況1與工況2，可以得出，隨著隧道埋置深度的減小，襯砌側部的受損部位出現了上移，且拱頂及側幫的受損程度也隨爆炸應力波強度的增大而變大。

工況3的最大主應變時程折線圖及數據的分析如圖10所示，損傷云圖見圖11。

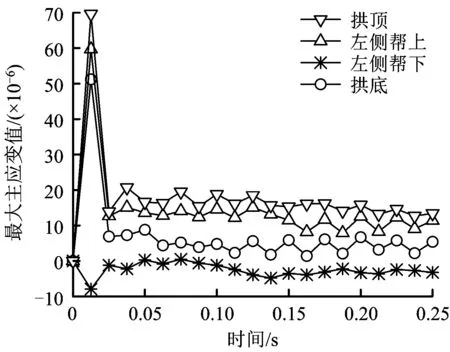
圖10 工況3最大主應變Fig.10 Maximum principal strain of working conditions 3

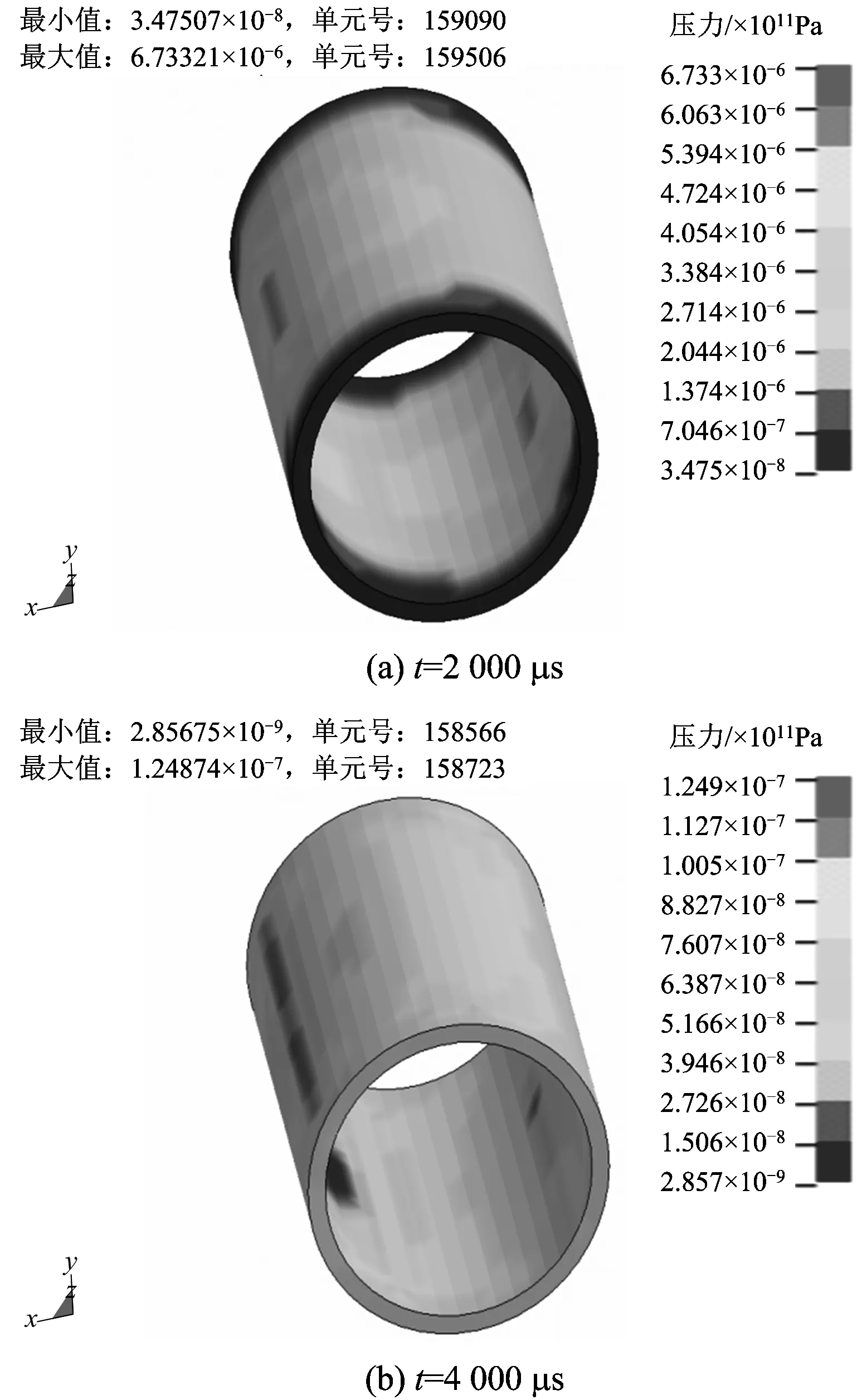
圖11 隧道埋深18 m時襯砌結構的損傷Fig.11 Lining structure damage for buried depth of tunnel as 18 m

由工況3襯砌結構最大主應變圖可知，隧道埋置深度為18 m時，各觀測部位最大主應變為70個拉應變，僅為工況1最大微應變的36%，可知結構局部沒有發生塑性變形。左側幫上側的最大主應變最大值為60個拉應變，低于可能出現破壞的限值100個微應變，拱底的最大主應變最大值為50個拉應變，同樣襯砌結構不會發生局部破壞。

進一步通過壓力損傷云圖11可直觀看出，襯砌結構徑向與橫向的損傷均有明顯削弱，局部未見損傷；綜合對比工況1～3，可以看出，襯砌結構側部單元的最大爆炸應力波強度隨隧道埋置深度的增加出現了明顯的下移，不同于頂爆時襯砌結構的易受損部位位于拱頂[16]，襯砌結構側幫同樣是外爆炸時應進行重點支護設計的部位。

結合不同側爆角度及隧道埋深，因拱頂及左側幫上部損傷較為嚴重，對最大主應變值進行對比，如表4～5所示。

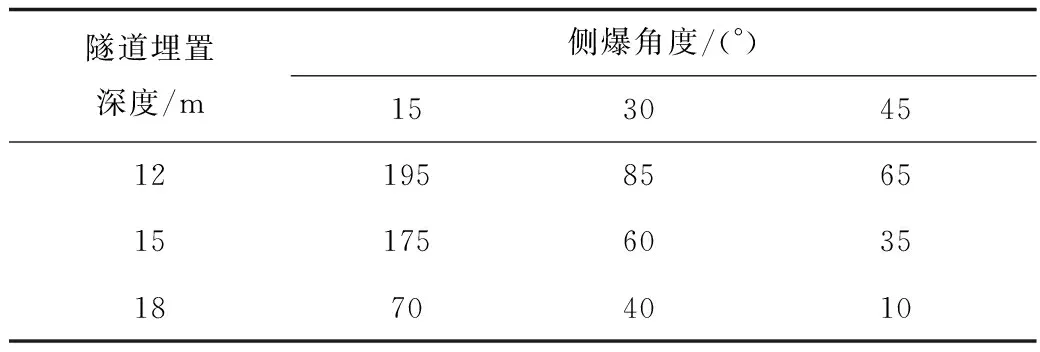
表4 拱頂最大主應變值Table 4 Maximum principal strain of vault

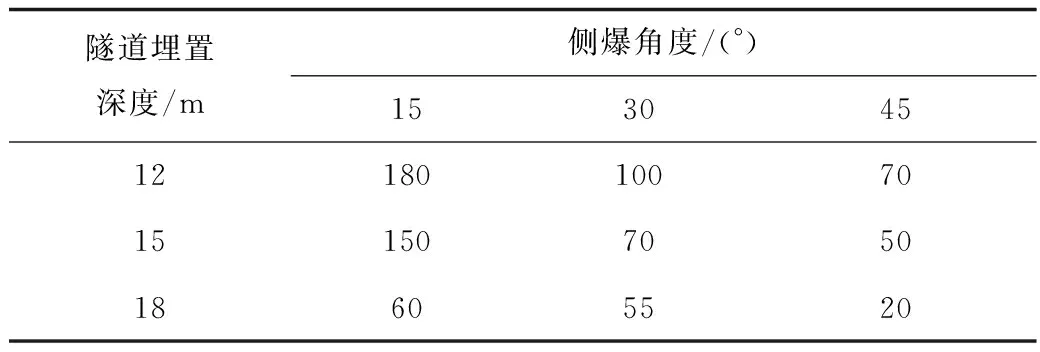
表5 左側幫上部最大主應變值Table 5 Maximum principal strain at upper left side

對比表4所示拱頂處不同側爆角度及埋深的最大主應變值，可以看出，當側爆角度為45°時，隨爆炸沖擊波距離的增加，隧道埋深18，12 m，衰減了77%；側爆角度為45°或隧道埋深為18 m時，襯砌結構的拱頂部位不會發生局部破壞；當隧道埋深為15 m，拱頂出現局部損傷僅為側爆角度為15°這一種情況；相較而言，當側爆角度為15°且埋深12 m時，拱頂局部最大主應變為195個微應變，可能出現危及襯砌結構整體的破壞。

對比表5所示左側幫處最大主應變值，可以看出，當側爆角度為45°或隧道埋深為18 m時，襯砌結構的左側幫部位不會發生局部破壞，即襯砌結構不會出現橫向的損傷；此外，與襯砌徑向拱頂的損傷情況一致，當隧道埋深為15 m，僅在側爆角度為15°時襯砌橫向會產生局部損傷；相較而言，當側爆角度為15°且埋深12 m時，將出現危及襯砌結構整體的破壞，此時最大主應變為180個微應變。

綜合對比表4～5，可以看出，隨著側爆角度的增加，襯砌結構左側幫的最大主應變值將逐漸大于拱頂部位，即襯砌結構橫向的損傷會逐漸大于徑向；而隨著隧道埋深的增加，襯砌結構橫向及徑向均有明顯的衰減。

4 結論

1)比對3組側爆工況，通過對所取觀測點的峰值響應值進行分析，可以看出：當側爆角度為15°及30°時，襯砌結構的徑向及橫向均有局部損傷，因角度為15°時局部破壞嚴重，導致了襯砌結構整體性的喪失。

2)對比側爆角度為變量的3組工況，通過特殊部位節點的主應變時程折線及襯砌結構損傷云圖分析襯砌結構損傷破壞形態，可以得出，爆炸距離決定著應力波總能量的大小，而襯砌結構的橫向損傷程度則由側爆角度與爆炸距離共同制約。

3)對比隧道埋深為變量的3組工況，通過最大主應變圖分析可知，隧道埋深12 m時左側幫上的單元僅為195個拉應變，埋深15，18 m分別衰減了10%，64%；進一步分析3組工況襯砌結構徑向及橫向的壓力損傷圖規律可知，隧道埋深12 m及15 m出現了破壞，埋深18 m未出現破壞。通過分析可得出：隧道埋深的增加削弱了徑向及橫向應力波的破壞能力，可以避免結構體局部出現過大損傷。

4)綜合來看，襯砌結構橫向的損傷并不弱于徑向，面臨爆炸源位于地面時襯砌結構的損傷效應問題，襯砌結構側幫及拱頂均應進行重點支護設計。避免結構局部的損傷引起結構整體的破壞。