多井系統復合油藏平均地層壓力計算方法研究

尹洪軍，文 剛，邢翠巧，付 京，Perapon Fakcharoenphol

(1.東北石油大學， 黑龍江 大慶 163318；2.提高油氣采收率教育部重點實驗室， 黑龍江 大慶 163318；3.Mewbourne School of Petroleum & Geological Engineering， The University of Oklahoma， Oklahoma Norman OK， USA 73019；4.Colorado School of Mines， Golden Colorado， USA 80401)

0 引 言

平均地層壓力是油田開發設計的一個重要參數，準確地分析出單井控制區域內的平均地層壓力水平是油田保持高產、穩產，進行各種措施調整的必要條件[1-3]。常用的確定平均地層壓力方法有MDH法、MBH法、迪茨(Dietz)法等[4-8]以及一些經驗公式，這些方法只適用于均質油藏平均地層壓力的計算，未考慮儲層的非均質性，也未考慮到注采比的影響。但是在油田全面投入開發之后，隨著井網加密和注水開采[9-12]，地下滲流狀況較油田開發早期發生了很大變化，注采不平衡使得油藏壓力受到注采比的影響[13]。實際油藏中井周圍儲層存在徑向復合儲層情況，近些年研究的考慮鄰井影響的平均地層壓力計算方法并不實用。因此，需要建立多井系統復合油藏的擬穩定流滲流數學模型，給出考慮注采比影響的多井系統復合油藏平均地層壓力的計算方法，保證多井注采情況下復合油藏的壓力評價更符合實際情況。

1 理論基礎

1.1 基本假設

無限大、等厚儲層中存在微可壓縮、黏度為常數的油水的流動；油水流度比為1，水平方向上的飽和度分布均一；儲層中有多口生產井和注水井(也可能沒有注水井)定量生產和定量注入，井的產量或注入量可以不同。在穩定生產時，每口井都自然地分成一定范圍的供給區域，如兩區復合油藏供給區域分為2個區域。關井前供給邊界或供給區域內的壓力隨時間變化具有某種上升或下降趨勢。兩區復合油藏物理模型如圖1所示。

1.2 數學模型的建立和求解

根據物質守恒原理可得：

(1)

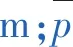
在線性壓力趨勢條件下，即t≥tpss(tpss為擬穩態出現時間，h)[14]，有：

(2)

圖1 兩區復合油藏物理模型示意圖

將式(2)代入式(1)得：

(3)

生產井的供給區域是以該井為中心的圓形兩區復合區域，建立線性壓力趨勢下的徑向流動數學模型：

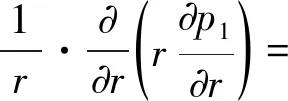
(4)

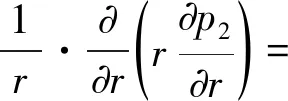
(5)

內邊界條件：

p(rw，t)=pwf(t)

(6)

外邊界條件：

(7)

兩區界面條件：

p1(a，t)=p2(a，t)

(8)

(9)

式中：pwf為井底流壓，MPa；p1、p2分別為1區和2區的地層壓力，MPa；μ為流體黏度，mPa·s；K1、K2分別為1區和2區的滲透率，D；r為地層某點到井底的距離，m；rw為井底半徑，m；a為復合半徑，m；re為邊界半徑，m。

求解數學模型式(4)—(9)，得到兩區復合油藏的地層壓力公式：

(10)

(11)

其中：

(12)

(13)

C1=λ[-Y2(1-RIP)a2+C]+Y1(1-RIP)a2

(14)

(15)

(16)

1.3 復合油藏平均地層壓力公式

用面積加權方法計算兩區復合油藏單井平均地層壓力：

(17)

將式(10)和式(11)代入式(17)，整理得：

(18)

式(18)即為兩區復合油藏的平均地層壓力計算公式。

當RIP=1時，式(18)轉換為式(19)，即為注采平衡時的復合油藏平均地層壓力公式，與水驅平均地層公式相同，從而驗證了該方法的正確性。

(19)

2 平均地層壓力敏感性分析

要獲得多井系統復合油藏考慮注采比影響的地層壓力，需利用油井壓力恢復測試資料解釋出該井控制區域內的儲層參數。在給定油井基本參數(產量或注入量、生產時間、有效厚度、孔隙度等)和儲層參數(滲透率、表皮系數等)情況下，當邊界壓力一定時，繪制出地層壓力分布曲線，并計算出單井平均地層壓力，基礎參數見表1。

表1 基礎參數表

圖2～4分別為不同因素影響下的地層壓力分布曲線。圖中的水平線為每一條地層壓力分布曲線對應的平均地層壓力。

2.1 注采比對單井地層壓力的影響

注采比分別為0.5、1.0和1.5，不同注采比條件下測試井地層壓力分布如圖2所示，對比結果見表2。

從圖2可以看出：邊界壓力一定時，注采比越大，井底壓力越大，平均地層壓力也越大；在復合半徑為62 m時，隨著注采比的增大，內區與外區壓力消耗速度變小，兩區界面壓力變化轉折點不明顯；井底附近壓力消耗速度最大，外區滲透率比內區低，外區壓力消耗速度較大。由表2可知，隨著注采比的增大，井底附近的壓力消耗速度減小，井底流壓增大。注采比大于1時，計算的平均地層壓力大于注采平衡時的平均地層壓力。一般油田注采比大于1，要得到準確的平均地層壓力，需要考慮注采比影響。

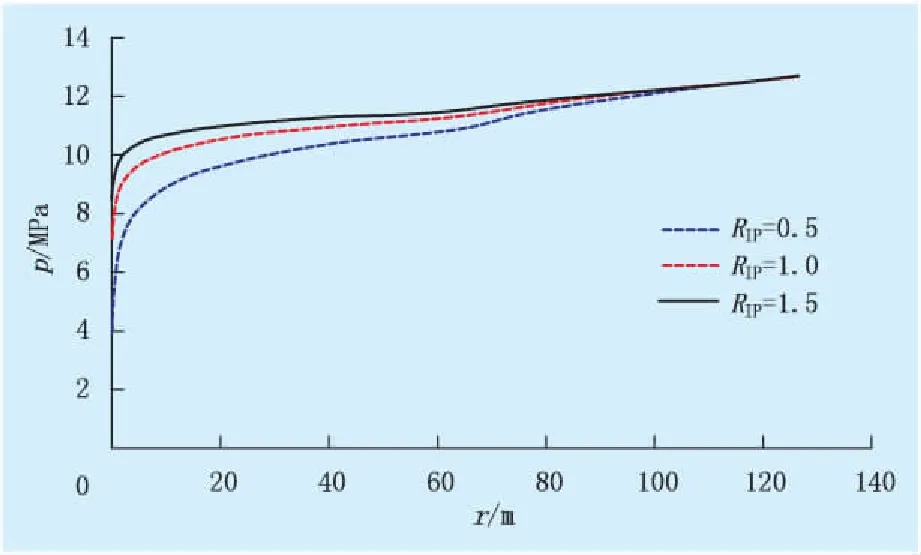
圖2 不同注采比條件下單井地層壓力分布曲線

注采比井底流壓/MPa平均地層壓力/MPa0.53.98411.7711.07.12211.9691.58.69112.069

2.2 流度比對單井地層壓力的影響

外區與內區的流度比(M)分別為0.22、0.32和0.42，其他參數一定時，不同流度比條件下測試井地層壓力分布如圖3所示，對比結果見表3。

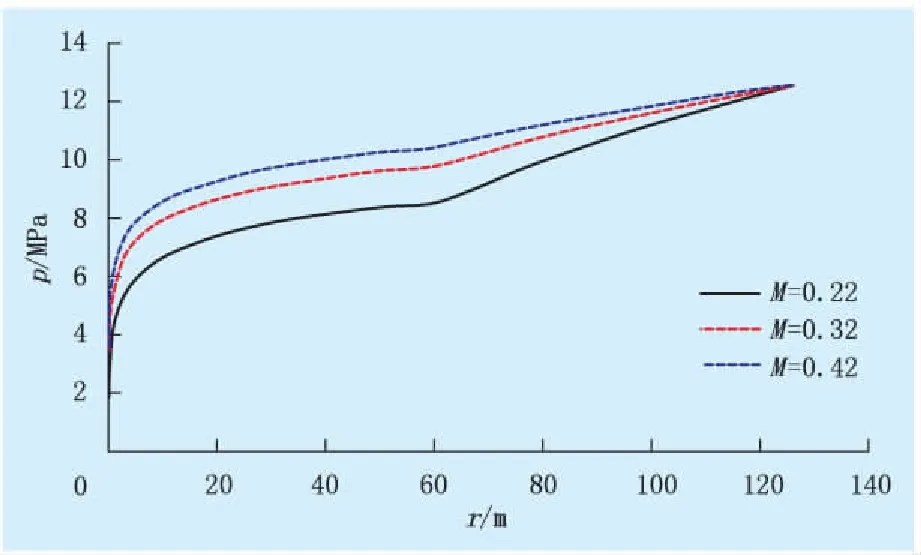
圖3 不同流度比條件下單井地層壓力分布曲線

流度比井底流壓/MPa平均地層壓力/MPa0.221.88510.6820.323.12611.2450.423.77711.539

由圖3可知：邊界壓力一定時，流度比越大，生產井附近的壓力消耗越小，注采井間的壓差越小；受到非均質性影響，在復合半徑為62 m處出現壓力變化轉折點；外區滲透率越小，壓力消耗速度越大。由表3可知：隨著流度比的增加，井底流壓和單井平均地層壓力依次增加，單井平均地層壓力的增加速度變小。

2.3 復合半徑對單井地層壓力的影響

復合半徑分別為62、73和88 m，其他參數一定時，不同復合半徑條件下測試井地層壓力分布如圖4所示，對比結果見表4。

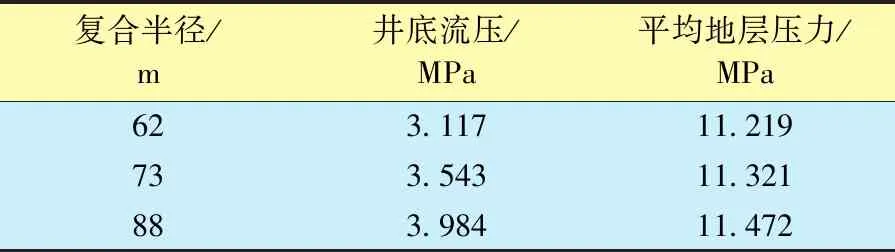
復合半徑/m井底流壓/MPa平均地層壓力/MPa623.11711.219733.54311.321883.98411.472

由圖4和表4可知：邊界壓力一定時，其他參數不變情況下，隨著復合半徑的增加，生產井的井底流壓和平均地層壓力都在不斷上升；不同復合半徑的外區地層壓力分布水平一致，復合半徑主要影響地層壓力分布曲線上翹時間；復合半徑越小，外區性質越差時，流體在內區流動時間越短，地層壓力分布曲線上翹時間越早。

3 實例應用

以喇嘛甸油田某口井為例，單井控制面積為0.1 km2，油層有效厚度為2.2 m。井周圍受到多口注水井影響，穩定生產0.5a后關井測壓力恢復，關井時間為71.333 h。日產液量為72.14 m3/d，含水為97.2%，流體黏度為0.835 2 mPa·s，油層中部流壓為4.099 MPa。利用曲線擬合方法解釋實測(lgΔp，lgΔp′)-lgt雙對數曲線(Δp為關井不同時刻壓差值，MPa；Δp′為關井不同時刻的壓力導數值，MPa/h)，雙對數曲線擬合結果如圖5所示。根據擬合得到的參數，利用公式(19)計算出該井控制范圍內的平均地層壓力為11.250 MPa，擬合參數和壓力計算結果見表5。注采比為1.30，地層存在多余能量補充，關井測得的末點壓力明顯大于實際平均地層壓力水平，注采平衡的水驅平均地層壓力則會偏小；實際計算的平均地層壓力(11.250 MPa)小于關井末點壓力(11.565 MPa)，同時大于不考慮注采比影響的水驅平均地層壓力(10.570 MPa)，說明考慮注采比影響，計算得到的平均地層壓力更符合實際地層壓力水平。

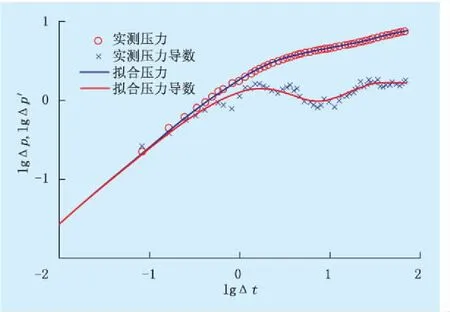
圖5 雙對數曲線擬合結果

參數數值滲透率/mD0.064復合半徑/m71.45流度比0.676表皮系數-1.370注采比1.30平均地層壓力/MPa11.250末點壓力/MPa11.565水驅平均地層壓力/MPa10.570

4 結 論

(1) 根據物質平衡原理，建立考慮注采比影響的多井系統復合油藏擬穩定滲流數學模型，并給出了平均地層壓力的計算方法。該方法適用于考慮注采比影響的多井系統復合油藏單井控制區域平均地層壓力的計算。

(2) 單井平均地層壓力的主要影響因素為：產量、滲透率、地層厚度、復合半徑和注采比。邊界壓力一定時，注采比越小，井間注采壓差越大，井底流壓和平均地層壓力越小；流度比越小，地層能量消耗越大，井底流壓和平均地層壓力越小；復合半徑影響內外區地層壓力分布上翹變化時間，外區地層各點壓力分布重合。

(3) 通過考慮注采比參數，可以更好地認識多井系統受到鄰井影響后的地層壓力水平。注采比大于1，地層有多余能量補充，關井測得的末點壓力明顯大于實際平均地層壓力水平，水驅平均地層壓力則會偏小，因此，該方法計算的平均地層壓力介于末點壓力和水驅平均地層壓力之間，更符合實際。