多假設多目標跟蹤算法

王 巖，蒿興華，楊順云

（解放軍31108 部隊，南京 210016）

多假設多目標跟蹤算法（MHT）是非常經典的多目標跟蹤算法，由Reid 在對雷達信號的自動跟蹤研究中提出，本質上是基于Kalman 濾波跟蹤算法在多目標跟蹤問題中的擴展。定義在k 時刻之前的檢測為Zk，多假設跟蹤的目標是基于已有軌跡對這種觀測關聯進行條件概率建模，把似然關聯假設Θik 劃分為當前關聯假設Θi（K）和k-1時刻的假設集合Θik（m）。可以利用貝葉斯推理得到關于關聯假設的后驗概率公式。

其中公式右側第一項表示基于前期假設集合和當前假設的觀察似然概率，即在歷史關聯的基礎上，當關聯Θivartheta_{I}（K）成立時，表現出當前觀測Z（k）的概率；第二項表示當前假設的似然概率，即在歷史關聯的基礎上，當前關聯假設的概率；第三項表示前期假設集合后驗概率。c 是貝葉斯公式中的分母，對于當前觀測已知的條件，可以認為是一個常數。總體的假設后驗概率可以表示為此三項的乘積。而公式第三項表示k-1時的后驗概率，因此，只考慮第一項和第二項就可以得到一個遞推公式。

如何對第一項和第二項進行建模？MHT 采用了二個概率模型：用均勻分布和高斯分布對關聯對應的檢測觀察建模；用泊松分布對當前假設的似然概率建模。

前者表示，當觀測是來自一個軌跡T 時，它符合T 的高斯分布，否則觀測是一個均勻分布的噪聲。后者表示，在誤檢和新對象出現概率確定的情況下，出現當前關聯的可能性可以通過泊松分布和二項分布的乘積表示。在以上假設下，關聯假設的后驗分布是歷史累計概率密度的連乘，轉化為對數形式，可以看出總體后驗概率的對數是每一步觀察似然和關聯假設似然的求和。因此，選擇最佳的關聯假設，轉化為觀察似然和關聯假設似然累計求和的最大化。在進行具體實現和優化的時侯，I.J.Cox 等人提出了一種基于假設樹的優化算法，如下圖所示。

圖中：左圖為k-3時刻三個檢測觀察和兩條軌跡的可能匹配。對于這種匹配關系，可以繼續向前預測兩幀，如圖右。得到一種三層的假設樹結構，對于假設樹根枝干的剪枝，得到k-3時刻的最終關聯結果。

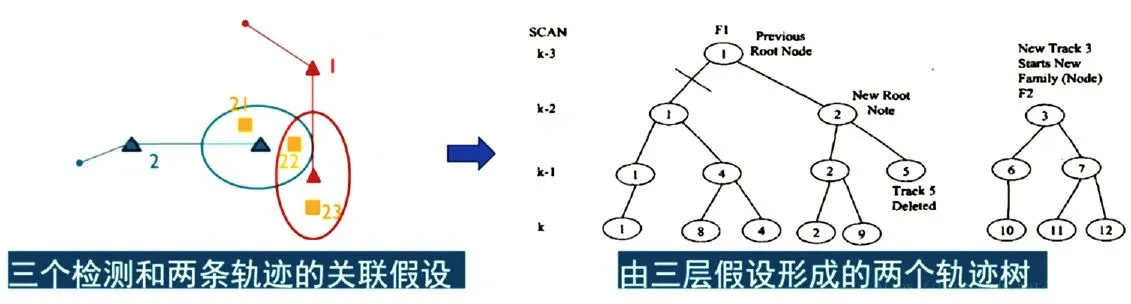
對于k 時刻的關聯對數似然概率，可以認為是k 時刻之前關聯觀察似然概率的對數求和，由于任何時刻都可能存在多種假設關聯，因此到k 時刻的假設構成了一種組合假設樹的層次關系。例如圖中左邊表示的是2個軌跡和3個觀測之間可能形成的關聯假設，可能存在的假設有{觀測23=＞軌跡1，觀測22=＞軌跡2，觀測21=＞新軌跡}或者{觀測22=＞軌跡1，觀測21=＞軌跡2，觀測23=＞新軌跡}，因此產生2個假設分支。圖中右側是從這2個關聯假設出發的三層假設樹關系，可以看出隨著假設層數的增多，關聯假設出現組合爆炸的可能。因此進行必要的剪枝減少假設空間的數目是必須的步驟。那么如何選擇最佳的關聯呢？I.J.Cox 采用了2個步驟來實現。首先，限制假設樹的層數為3層。其次，是對每個分支的葉節點概率對數進行求和，最大的分支進行保留，即選擇邊緣概率最大的那個分支假設作為最后選擇的關聯。

采用基于均勻分布、泊松分布以及高斯分布的模型，可以高效快速計算選擇k-3時優化的假設關聯。這種基于似然概率對數累加的方法雖然方便迅速，但是存在一個主要的限制，即假定觀測關聯符合高斯模型，并且在每一步選擇關聯假設之后，需要利用Kalman 濾波更新軌跡狀態。通過對MHT 基本公式的擴展，可以建立不同的概率模型描述這種多假設關聯的全局概率，例如Kim 等人在ICCV2015和ECCV2018通過歸一化的最小均方差優化算法引入表觀模型來擴展MHT 算法，取得不錯的多行人跟蹤結果。