懸索橋纜索鋼絲損傷超聲導波檢測數值模擬

張東波，王波，汪正興，王梓宇

懸索橋纜索鋼絲損傷超聲導波檢測數值模擬

張東波1,2，王波1,2，汪正興1,2，王梓宇1,2

(1. 中鐵大橋科學研究院有限公司，湖北武漢 430034；2. 橋梁結構健康與安全國家重點實驗室，湖北武漢 430034)

為了實現對大跨懸索橋纜索鋼絲損傷的有效檢測，采用理論分析和數值模擬相結合的方法，對超聲導波無損檢測技術進行研究。通過理論求解鋼絲中導波的頻散曲線，分析頻散特性和波結構，選取中心頻率為200 kHz的L(0,1)模態進行鋼絲斷絲損傷檢測；利用有限元軟件，研究了鋼絲中導波的頻散特性和波結構，通過二維傅里葉變換技術對鋼絲中的低階導波模態進行識別，進一步分析了缺陷尺寸和角度對L(0,1)模態缺陷反射系數的影響；最后，對L(0,1)模態在兩根鋼絲和七根鋼絲的斷絲處的缺陷回波進行了數值模擬。數值模擬與理論分析結果相吻合，說明低頻L(0,1)模態可以有效地對纜索鋼絲斷絲損傷進行遠距離檢測。

懸索橋；纜索體系；超聲導波；頻散特性；數值模擬；損傷檢測

0 引言

纜索體系作為大跨度橋梁的主要承載結構，是懸索橋的生命索，直接關系到橋梁的安全和使用壽命。由于纜索體系長期承受交變載荷并暴露于自然環境中，索內鋼絲極易發生疲勞、腐蝕、斷絲損傷[1-3]。鋼絲損傷使得纜索有效金屬承載面積減小，將嚴重降低結構的安全性和耐久性，造成橋梁結構發生災難性的突發事故，例如波因特普萊森特(Point Pleasant)懸索橋倒塌、庫爾勒孔雀河大橋垮塌、武夷山橋梁坍塌等事故均與纜索體系失效有關。為了保障大跨度橋梁的安全性與耐久性，針對纜索鋼絲損傷，特別是纜索內部鋼絲損傷，急需一種有效的無損檢測方式。常用的纜索檢測技術主要有：聲發射法、射線檢測法、漏磁檢測法和超聲導波法等[4]。聲發射技術可以實現動態實時監測，但檢測精度低；射線技術可檢測纜索自由部分和錨固區鋼絲的缺陷，但檢測效率低、成本高、存在輻射污染；漏磁技術可檢測纜索自由部分的外圍鋼絲缺陷，但無法檢測纜索內部鋼絲的缺陷。超聲導波在波導中傳播時，橫截面全部質點均參與振動，可以遠距離檢測纜索的內、外部缺陷，在大跨懸索橋纜索鋼絲損傷檢測方面具有廣闊的應用前景。

細長圓桿中超聲導波的傳播規律是研究拉索損傷檢測的基礎，ROSE等[5]首先對圓桿中導波的各種模態進行了理論推導，求解了頻散方程。圓桿中的超聲導波在損傷檢測方面具有廣泛應用。MIJAREZ等[6]研究了輸電線中超聲導波的傳播特性，利用低階模態對輸電線鋁絲人工刻槽進行了檢測。BENMEDDOUR等[7]將有限元和半解析有限元方法相結合，提出了一種三維混合方法，分析了鋼柱中縱向、扭轉和彎曲模態導波在不同深度裂紋缺陷處的反射波和散射波，為裂紋檢測和表征提供了指導。BARTOLI等[8]利用半解析有限元法計算了鋼絲中導波的頻散曲線，利用三維有限元法研究了低頻導波在鋼絞線中的傳播特性。元軍會等[9]利用有限元方法模擬了低階縱向導波在鋼筋中的傳播規律，對缺陷進行了準確識別與定位。XU等[10]通過電磁超聲在鋼絲中激發L(0, 1)模態對纜索斷絲損傷進行了檢測。劉增華等[11]利用L(0, 2)模態對鋼絞線人工缺陷進行了有效檢測，并通過缺陷回波幅值對缺陷大小進行表征。潘永東等[12]利用有限元方法研究了L(0, 6)模態在鋼絲中的傳播速度，通過實驗對拉索錨固區損傷進行了有效檢測。超聲導波在鋼絲中的傳播規律對于大跨懸索橋纜索檢測損傷具有重要的指導意義，但目前關于導波在多根鋼絲中傳播特性的數值模擬研究的報道還較為少見。

本文通過理論分析和數值模擬相結合的方法研究鋼絲中導波模態的傳播特性，分析導波的頻散特性和波結構，旨在選取合適的導波模態進行大跨懸索橋纜索鋼絲斷絲損傷檢測，并進一步討論斷絲缺陷尺寸和角度對缺陷反射系數的影響。

1 理論分析

大跨懸索橋纜索中彈性波傳播特性十分復雜，其研究基礎為單根鋼絲中導波的傳播特性。單根鋼絲可視為細長圓桿，基于柱坐標系對鋼絲中聲傳播問題進行描述，如圖1所示，其中方向與桿的軸向重合。

圖1 柱坐標系下實心圓桿模型

在超聲導波檢測中，由于頻散效應，波包隨傳播距離的增加而逐漸變寬，幅值逐漸變小，不利于缺陷的定位和判斷。為了減小頻散的影響，一般采用窄帶信號，并選取頻散曲線上較為平坦的部分進行激勵。因此，導波檢測中需要解決的關鍵問題是選取單模態和非頻散區域的模態頻率。

1.1 頻散曲線

根據彈性波理論，桿狀結構中存在3種模態的導波：縱向、扭轉和彎曲模態。基于柱坐標系下的Navier方程，利用勢函數及邊界條件，可以推導出導波的頻散方程[5]。通過迭代算法求解頻散方程，可以計算出桿狀結構中不同導波模態的相速度和群速度頻散曲線。

假定鋼絲的幾何尺寸和材料參數如表1所示，鋼絲中導波的相速度和群速度頻散曲線分別如圖2(a)和2(b)所示，其中藍色、紅色和綠(紫)色曲線分別表示縱向、扭轉和彎曲模態。觀察圖2可知，鋼絲中除了T(0, 1)模態是非頻散的，其他模態均存在頻散現象；不同的導波模態，頻散程度不同；同一導波模態在不同的頻率范圍，頻散程度亦不同。在相當寬的頻率范圍20～400 kHz內，L(0, 1)模態的群速度大于其他模態，也就是說該模態在鋼絲中傳播時，最先被接收到，易與其他導波模態相分離。同時，L(0, 1)模態在頻率范圍20～250 kHz內，頻散效應弱，有利于其波形信號的識別與分析，可用于鋼絲周向缺陷的檢測。T(0, 1)模態在低頻范圍20 kHz～1 MHz內，回波信號能量集中，可用于鋼絲軸向缺陷的檢測。

表1 鋼絲的半徑和材料參數

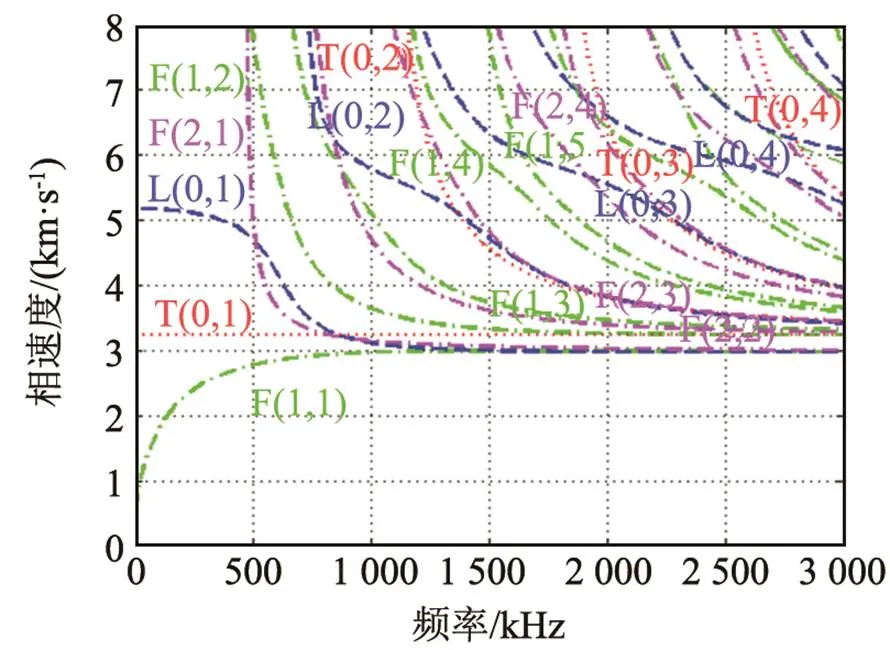
(a) 相速度

(b) 群速度

圖2 鋼絲中超聲導波頻散曲線

Fig.2 Dispersion curves of ultrasonic guided wave in steel wire

1.2 波結構

桿狀結構中導波各模態軸向位移的大小與檢測周向缺陷的靈敏度成正比。同時，各模態在傳播過程中的能量泄漏與桿表面的徑向位移成反比，因此，研究導波的波結構對于選取合適的導波模態進行損傷檢測至關重要。

本文研究的是醫院的科研經費支出的內部控制，但完善各管理系統、加強預算控制、強化標準定額管理等方法在其他支出管理中也有較強的共通性，故本文的研究成果對醫院支出的內部控制也有參考作用。

通過理論計算鋼絲中L(0, 1)模態在不同頻率下的波結構，計算結果如圖3所示。由圖3可見，軸向位移占主導，說明L(0, 1)模態在鋼絲中心位置處的能量集中，對于斷絲這類周向缺陷檢測靈敏度高。與圖3(b)中400 kHz的波結構相比，200 kHz的軸向位移更大，徑向位移ur在鋼絲表面更小，說明200 kHz的L(0, 1)模態對于周向缺陷更加敏感，且在鋼絲中傳播時，能量衰減少，傳播距離遠，因而適合于大跨度懸索橋纜索斷絲的遠距離檢測。

(a) 200 kHz

(b) 400 kHz

圖3 L(0, 1)模態波結構的理論計算結果

Fig.3 Theoretical calculation results of the wave structure of L(0,1) mode

1.3 激發信號

選用漢寧窗調制的正弦脈沖信號模擬激勵源，表達式為

(1)

其中，f為激勵源的中心頻率，n為周期數，t為時間，R(t)是矩形窗函數。為了提高檢測能力，避免漏檢現象，本文選取周期數n=10。

1.4 導波衰減

導波在波導中傳播的衰減值計算表達式為

(2)

其中，為參考波形的峰峰值，M為導波在波導中傳播一定距離L后的峰峰值。

1.5 導波信號

為便于分析，本文忽略鋼絲中由材料本身的阻尼效應引起的導波衰減和頻散現象，假設鋼絲的長度為2 000 mm。選擇中心頻率為200 kHz和400 kHz的信號作為激勵源，沿軸向z施加在鋼絲端部，L(0, 1)模態信號分別如圖4(a)和4(b)所示，其中A是激勵信號，C是2 000 mm處導波信號。從圖4中可以看出，與原始信號A相比，200 kHz的L(0,1)模態波包C的寬度和幅度均無明顯變化，而400 kHz的波包C在2 000 mm處的寬度增加，幅值降低，說明L(0,1)模態在400 kHz附近存在嚴重的頻散現象，與頻散曲線的結論一致。通過式(2)計算可知，200 kHz的L(0,1)模態信號的衰減是0.13 dB·m-1，400 kHz信號的衰減是7.67 dB·m-1。通過互相關聲時計算方法[13]，可得200 kHz的L(0,1)模態的傳播速度是5 042.5 m·s-1，與頻散曲線中群速度值5 048.4 m·s-1比較一致。

(a) 200 kHz

(b) 400 kHz 圖4 L(0, 1)模態激發和接收波形的理論計算結果 Fig.4 Theoretical calculation results of the excited and received waveforms of L (0, 1) mode 2 三維數值模擬 三維有限元模型考慮了聲場分布的三維特性，可以完整地預測彈性波在計算區域中的傳播過程，具有較高的計算精度。 2.1 數值模型 本文在數值模擬中采用三角網格劃分計算區域，網格尺寸滿足，其中為鋼絲中導波的相速度，為激發源的最大頻率，同時，在時域中進行數值求解，時間步長滿足，根據鋼絲的長度選擇求解的時間域。激勵源信號形式如式(1)所示，按不同的方式施加在鋼絲端面，可以激發出不同的導波模式。導波信號與接收區域中質點的振動有關，可以通過對相應區域內的位移進行積分來模擬。 2.2 L(0, 1)模態頻散特性分析 根據桿狀結構的聲傳播理論，在鋼絲的端面沿軸向z施加激勵可以激發出縱向模態，通過在時域中進行數值模擬，可以計算鋼絲中的位移場。 基于問題的學習模式 20世紀60年代，McMaster University Medical School把基于問題的學習模式（Problembased learning，PBL）真正引入教育中并逐漸推廣應用。英文中關于“問題”主要有“problem”和“question”?！督逃筠o典》中把問題（problem）也稱作“難題”，需要依據策略和知識經驗重新組合。而簡單的問題（question）可依據已有的知識立即做出應答[4]。基于問題的學習模式中的“問題”（problem）指的是學習情境，學習者必須付出一定的努力才能達到教學目標，故用“problem”而非“question”。 在數值模擬中鋼絲的幾何尺寸和材料參數如表1所示，其中鋼絲長度為1 000 mm。當中心頻率為200 kHz和400 kHz的激勵源沿鋼絲軸向z施加于端面上時，鋼絲端面的軸向位移隨時間的變化關系分別如圖5(a)和5(c)所示，對應的頻譜分別如圖5(b)和5(d)所示，其中A為激勵信號，C為導波信號。圖5(a)中導波信號C在鋼絲中傳播時，與激勵信號A相比，幅值和寬度均沒有明顯變化，說明導波信號C在200 kHz附近頻散效應弱，計算可得導波的傳播速度為5 046.7 m·s-1，與L(0, 1)模態理論群速度5 048.5 m·s-1的相對誤差為0.04%。觀察頻譜圖5(b)可知，頻率成分主要分布在200 kHz左右，帶寬范圍是[183.7 213.4] kHz，與公式(1)中200 kHz激勵源的頻率范圍一致。觀察圖5(c)可知，400 kHz的導波信號C在鋼絲中傳播時，與原始信號A相比，其幅值下降，寬度變寬，說明導波信號C在400 kHz附近頻散效應強。通過式(2)計算可知200 kHz的L(0, 1)模態的幅度衰減是0.25 dB·m-1，400 kHz的L(0, 1)模態的衰減是6.64 dB·m-1，與圖4中的理論結果相吻合。 為了對導波模態進行識別，針對不同的激勵源施加方式，采用二維傅里葉變換技術對鋼絲中沿軸向不同位置處的軸向位移進行后處理，得到如圖6所示的波數-頻率圖，其中藍色曲線表示L(0, 1)模態的理論頻散曲線，黑色區域表示軸向位移的二維傅里葉變換結果。觀察圖6中的藍色曲線可知，100、200和400 kHz導波信號的二維傅里葉變換系數的較大值，即對應的能量，沿L(0, 1)模態的頻散曲線分布，說明此時鋼絲中傳播的導波模態為L(0, 1)。觀察圖6中的紅色和綠色曲線可知，鋼絲中傳播的T(0, 1)和F(1, 1)模態二維傅里葉變換系數的較大值沿各自的頻散曲線分布，驗證了所建立導波數值模型的合理性和準確性。 在該人行天橋建設中，在橋梁頂面需要設置透明雨棚，避免行人行走時受到雨水影響。雨棚選用輕質透明PC耐力板，不僅柔軟度比較高，而且更加美觀。在橋梁排水方面，主橋采用縱坡自然排水方式。 (a) 200 kHz (b) 200 kHz (c) 400 kHz (d) 400 kHz 圖5 L(0, 1)模態激發和接收波形的數值模擬結果 Fig.5 Numerical simulation results of the excited and received waveforms of L(0, 1) mode 圖6 鋼絲中超聲導波的波數-頻率圖 Fig.6 Wavenumber-frequency diagram of ultrasonic guided waves in steel wire 3 單根鋼絲損傷檢測 當超聲導波在鋼絲中傳播時，遇到缺陷會發生波的反射、透射和模態轉換等現象，產生攜帶缺陷信息的反射波。通過對反射信號的波形、幅值、波包等指標進行分析，可以判斷鋼絲中是否存在缺陷，以及缺陷存在的位置和大小。 3.1 缺陷定位 本文在數值模擬中利用凹槽來模擬鋼絲中的斷絲缺陷。圖7(a)和7(b)分別為無缺陷和有缺陷時，L(0, 1)模態在鋼絲中傳播時某一時刻的軸向位移場快照，從圖中可以觀察到，當L(0, 1)模態傳播至缺陷時，產生了明顯的反射波。 (a) 無缺陷 (b) 有缺陷 圖7 鋼絲中某一時刻z方向的位移場uz Fig.7 The displacement field uz along the z direction at a certain time in steel wire 通過圖8所示的自發自收方式，利用飛行時間法對鋼絲缺陷進行檢測。假設鋼絲長為l，缺陷位置距接收端長，完好鋼絲底端一次回波時間為t，則根據可計算出導波傳播波速v。假設有缺陷鋼絲中一次缺陷回波時間為，則根據可定位缺陷的位置。 采用SPSS 20.0統計學軟件對數據進行處理，計數資料以百分數（%）表示，采用x2檢驗，計量資料以“±s”表示，采用t檢驗，以P＜0.05為差異有統計學意義。 圖8 L(0, 1)模態在缺陷鋼絲中的傳播示意圖 Fig.8 Schematic diagram of the propagation of L (0, 1) mode in steel wire with defects 數值模擬中取鋼絲半徑r=2.5 mm，長度l=1 000 mm，缺陷徑向深度h=1 mm，軸向寬度d=1 mm，缺陷位于鋼絲的中間=500 mm處，激勵源的中心頻率為200 kHz。圖9(a)是L(0,1)模態在鋼絲激勵端面的軸向位移響應，其中A為激勵，C為導波信號，B為缺陷反射波，根據其到達時間約為200.80 μs和L(0, 1)模態的傳播速度，可以定位缺陷所在位置為502.88 mm，與實際缺陷位置l1=500 mm的誤差為0.58%。圖9(b)和9(c)分別是缺陷徑向深度h=2.5、4 mm時，L(0, 1)模態在鋼絲激勵端面的軸向位移響應，缺陷回波B的傳播時間、定位的缺陷位置及其與實際位置的誤差如表2所示。 表2 基于L(0, 1)模態定位鋼絲斷絲缺陷數值模擬結果 Table 2 Numerical simulation of defect location in steel wire based on L (0, 1) mode 頻率/Hzh/mml1/mmt/μs位置/mm誤差/% 2001.0500200.80502.880.58 2.5500199.70501.620.36 4.0500198.50501.500.30 觀察圖9可知，隨著缺陷深度h的增加，缺陷反射波B的幅值逐漸增加，導波信號C的幅值逐漸減小，說明了L(0, 1)模態對于缺陷深度較敏感。同時，觀察表2可知，隨著缺陷深度h的增加，缺陷位置的測量誤差逐漸減小。 葉靄玲顯然并不真正想要離開我，否則她就不會到我父母面前告狀，也不會把自己的情緒反應公然呈現在她自己父母眼里。說到底，我們之間已經有了那回事，這對我來說也許還無所謂，但是對于她可是一件難以彌補的缺失。面對我的求饒，她的反應很微妙，既不同意也不否決，她是要看我的行動，以觀后效。說白了，就是要把我架在火上烤，看我能不能經受得住她對我的考驗。這可真像是把我掛在樹上，用玫瑰花刺束成的枝條抽我一樣。我發生這樣的聯想，內心里有一種自我犧牲的悲壯情懷，雖然我知道其實自己很混蛋。 3.2 缺陷尺寸識別 定義鋼絲中導波的反射系數為，透射系數為，其中為缺陷回波幅值，為缺陷處透射波幅值，為導波的激勵波幅值。在不考慮能量耗散的情況下，導波的反射系數和透射系數應滿足等式，可以通過反射系數的大小判斷鋼絲中缺陷尺寸，反射系數越大，缺陷越明顯。 為了分析缺陷軸向寬度d與徑向深度h對反射回波的影響，通過數值模擬計算200 kHz時的L(0, 1)模態反射系數隨不同寬度和深度缺陷的變化曲線，結果如圖10所示。從圖10中可以看出，隨著缺陷寬度的增加，反射系數先變大后變?。浑S著缺陷深度的增加，反射系數逐漸增大，并且缺陷越深，反射回波幅值越大。通過對比反射系數隨缺陷寬度和深度的變化關系可知，L(0, 1)模態對缺陷深度更加敏感。 (a) h=1.0 mm (b) h=2.5 mm (c) h=4.0 mm 圖9 不同缺陷徑向深度的L(0, 1)模態軸向位移響應 Fig.9 The axial displacement response of L (0, 1) mode for different defect radial depths 從圖10可以看出，當缺陷軸向寬度d為6 mm或7 mm時，反射系數開始衰減，這是由于當L(0, 1)模態傳播至缺陷時，缺陷的前后端面將產生不同的導波同時向接收端傳播。兩列導波傳播的路程差為缺陷長度的2倍，即與200 kHz的L(0,1)模態的半波長12.7 mm相等時，將產生波的干涉現象，使得鋼絲質點的振動減弱，反射系數減小。 圖10 反射系數Cr隨缺陷軸向寬度d和徑向深度h變化曲線 Fig.10 The variation curve of the reflection coefficient Cr with the axial width d and the radial depth h of the defect 3.3 缺陷信號隨缺陷角度的變化關系 為了分析缺陷深度h與偏轉角θ對反射回波的影響，通過數值模擬計算200 kHz的L(0, 1)模態反射系數隨不同深度和偏轉角缺陷的變化曲線，如圖11所示，其中缺陷的軸向長度d為1 mm。觀察圖11可知，隨著缺陷偏轉角從-30°增加到30°，反射系數先變大后變??；對于同一偏轉角，隨著缺陷深度的增加，反射系數逐漸增大，并且缺陷越深，反射回波的幅值越大。通過對比反射系數隨缺陷深度和偏轉角的變化關系可知，L(0, 1)模態對于缺陷深度更加敏感。 圖11 反射系數Cr隨缺陷徑向深度h和偏轉角度θ變化曲線 Fig.11 The variation curve of the reflection coefficient Cr with the radial depth h and the deflection angle θ of the defect 4 多根鋼絲損傷檢測 4.1 兩根鋼絲 數值模擬中取兩根平行鋼絲，如圖12(a)所示，其中鋼絲半徑r為2.5 mm，長度l為500 mm，激勵源的中心頻率為200 kHz。在兩根鋼絲端部沿軸向均施加激勵源，在時域中對鋼絲位移場進行求解。圖12(a)是導波模態在鋼絲激勵端面的軸向位移uz響應，其中A為激勵波，C為導波信號，根據C的到達時間204.72 μs，可以計算導波模態的傳播速度為4 884.72 m·s-1。 取缺陷徑向深度h=2.5 mm，軸向寬度d=1.0 mm，缺陷位于一根鋼絲的=300 mm處。圖12(b)是L(0, 1)模態在鋼絲激勵端面的軸向位移隨時間的變化關系，其中B為缺陷反射波。根據B的到達時間124.38 μs和L(0, 1)模態的傳播速度，可以定位缺陷所在位置為303.46 mm，與實際缺陷位置=300 mm的誤差為0.69%。 基于二維傅里葉變換技術對兩根鋼絲中傳播的導波模態進行識別，得到的波數-頻率圖如圖13所示，其中藍色曲線表示單根鋼絲中L(0, 1)模態的理論頻散曲線，黑色區域表示兩根鋼絲中軸向位移的二維傅里葉變換結果。觀察圖13可知，二維傅里葉變換系數的較大值，沿L(0, 1)模態的頻散曲線分布，說明了此時鋼絲中傳播的導波為L(0, 1)模態。 我國執業藥師發展歷程還較短，各項法律法規、制度建設還有待完善。從執業藥師注冊數據進行探析可見一斑。執業藥師的準入條件偏低、執業能力欠缺、數量不足、誠信體系不完善、公眾對執業藥師的認知度、認可度不高，都是阻礙執業藥師發展的主要問題。我們一方面要努力提升執業藥師的專業素質、服務能力，增強公眾對執業藥師的認可；另一方面要加大對執業藥師的宣傳，多渠道發揮藥學服務作用，增強公眾對執業藥師的認知，引導公眾主動向執業藥師尋求用藥指導，有效減少不合理用藥及發揮醫?？刭M作用，真正使執業藥師成為“實施健康中國戰略”的重要力量。 (a) 無缺陷 (b) 有缺陷 圖12 兩根鋼絲中有或沒有缺陷時的L(0, 1)模態軸向位移響應 Fig.12 The axial displacement responses of L (0, 1) mode in the two steel wires with or without defect 圖13 兩根鋼絲中L(0, 1)模態的波數-頻率圖 Fig.13 Wavenumber-frequency diagram of L(0, 1) mode in two steel wires 4.2 7根鋼絲 數值模擬中取7根平行鋼絲，半徑r為2.5 mm，長度l為500 mm，激勵源的中心頻率為200 kHz。在7根鋼絲端部沿軸向均施加式(1)所示的激勵源，在時域中對鋼絲位移場進行求解。圖14(a)是導波模態在鋼絲激勵端面的軸向位移響應，其中A為激勵波，C為導波信號，根據C的到達時間215.68 μs，可以計算導波模態的傳播速度為4 636.55 m·s-1，小于單根鋼絲中L(0, 1)模態的理論群速度。 取缺陷徑向深度h=2.5 mm，軸向寬度d=1.0 mm，缺陷位于中心鋼絲=300 mm處。圖14(b)是L(0, 1)模態在鋼絲激勵端面的軸向位移響應，其中B為缺陷波。根據B的到達時間130.82 μs和導波模態的傳播速度4 636.55 m·s-1，可以定位缺陷所在位置為303.27 mm，與實際缺陷位置=300 mm的誤差為1.09%。 (a) 無缺陷 (b) 有缺陷 圖14 7根鋼絲中有或沒有缺陷時的L(0,1)模態軸向位移響應 Fig.14 The axial displacement response of L (0,1) mode in the seven steel wires with or without defect 基于二維傅里葉變換技術對7根鋼絲中傳播的導波模態進行模式識別，得到的波數-頻率圖如圖15所示，其中藍色曲線表示單根鋼絲中L(0, 1)模態的理論頻散曲線，黑色區域表示7根鋼絲中軸向位移的二維傅里葉變換結果。觀察圖15可知，二維傅里葉變換系數的較大值，沿L(0, 1)模態的頻散曲線分布，說明了此時鋼絲中傳播的導波為L(0, 1)模態。 圖15 7根鋼絲中L(0, 1)模態的波數-頻率圖 Fig.15 Wavenumber-frequency diagram of L(0, 1) mode in seven steel wires 取缺陷徑向深度h=4 mm，軸向寬度d=1 mm，當缺陷分別位于中心和外圍鋼絲l1=300 mm處時，L(0, 1)模態在鋼絲激勵端面的軸向位移響應分別如圖16(a)和16(b)所示。圖16(a)和16(b)中B到達時間分別為130.45 μs和131.63 μs，可以定位缺陷所在位置為302.42 mm和305.61 mm，與實際缺陷位置=300 mm的誤差分別為0.81%和1.67%。 (a) 缺陷位于中心鋼絲 > (b) 缺陷位于外圍鋼絲 圖16 7根鋼絲中不同缺陷位置的L(0, 1)模態軸向位移響應 Fig.16 The axial displacement responses of L (0,1) mode to different defect positions in seven steel wires 5 結論 本文利用理論分析和數值模擬研究了鋼絲中縱向模態的傳播特性和波結構，并選擇L(0, 1)模態對單根和多根鋼絲中的斷絲缺陷進行了檢測，得出了以下結論： (3)成都平原城市群各經濟類型數目呈波動性變化，經濟發達型分布在以成都市為核心的縣域，經濟較發達型分布在成都市區的外圍，大部分區域屬于經濟中等型和經濟滯后型，主要分布在研究區邊緣地帶，但研究區整體經濟空間發展格局逐步趨于穩定，呈“凸”字型空間分異格局.從經濟實力結構看，從2000年的“金字塔型”逐步轉變為“橄欖型”結構. 該團領導干部、“兩委”人員認真觀看聆聽習近平主席重要講話，倍受鼓舞，反響強烈。大家紛紛表示，改革開放只有進行時，沒有完成時，我們將更加努力，投身到服務人民群眾中去，刻苦奮斗，積極作為。 (1) 通過理論分析和數值模擬求解了單根鋼絲中導波的頻散曲線和波結構，分析了不同頻率L(0, 1)模態的傳播規律，說明了200 kHz的L(0, 1)模態的頻散效應弱且對周向缺陷敏感，適合用于鋼絲斷絲損傷的遠距離檢測。 (2) 利用三維數值模擬研究了單根鋼絲中L(0, 1)模態與斷絲缺陷的作用規律，通過二維傅里葉變換對L(0, 1)模態進行了識別，分析了缺陷反射系數隨缺陷尺寸和角度的變化規律，說明了缺陷深度對于反射系數的主導作用。 (3) 通過對兩根和7根鋼絲中斷絲損傷的精確定位，說明了低頻縱向模態可用于大跨懸索橋纜索損傷的遠距離檢測。 參考文獻 [1] 溫文峰, 張宇峰, 馬愛斌, 等. 懸索橋主纜的腐蝕與防護[J]. 腐蝕與防護, 2007, 28(11): 598-601. WEN Wenfeng, ZHANG Yufeng, MA Aibin, et al. Corrosion and protection of main cables of suspension bridges[J]. Corrosion & Protection, 2007, 28(11): 598-601. [2] 葉覺明, 李榮慶. 現代懸索橋主纜防護現狀與展望[J]. 橋梁建設, 2009, 5(6): 67-71. YE Jueming, LI Rongqing. State-of-the-art and prospecting of main cable protection of modern suspension bridges[J]. Bridge Construction, 2009, 5(6): 67-71. [3] 白山云, 陳開利, 陳杰, 等. 公路懸索橋預防性養護技術[J]. 橋梁建設, 2014, 44(2): 101-106. BAI Shanyun, CHEN Kaili, CHEN Jie, et al. Preventive maintenance techniques for highway suspension bridge[J]. Bridge Construction, 2014, 44(2): 101-106. [4] 武新軍, 賁安然, 徐江. 橋梁纜索金屬損傷無損檢測方法[J]. 無損檢測, 2012, 34(4): 12. WU Xinjun, BEN Anran, XU Jiang. Nondestructive testing method for metallic flaws of bridge cables[J]. Nondestructive Testing, 2012, 34(4): 12. [5] ROSE J L, 何存富, 吳斌, 等. 固體中的超聲波[M]. 北京: 科學出版社, 2004. ROSE J L, HE Cunfu, WU Bin, et al. Ultrasonic waves in solid media[M]. Beijing: The Science Press, 2004. [6] MIJAREZ R, BALTAZAR A. Guided wave propagation study in an ACSR cable with artificial damage[C]//AIP Conference Proceedings, 2013, 1511(1): 1417-1424. [7] BENMEDDOUR F, TREYSSèDE F, LAGUERRE L. Numerical modeling of guided wave interaction with non-axisymmetric cracks in elastic cylinders[J]. International Journal of Solids and Structures, 2011, 48(5): 764-774. [8] BARTOLI I, CASTELLAZZI G, MARZANI A, et al. Prediction of stress waves propagation in progressively loaded seven wire strands[J]. The International Society for Optical Engineering, 2012, 8345(5): 5-12. [9] 元軍會. 鋼筋腐蝕損傷超聲導波檢測技術[D]. 大連: 大連理工大學, 2013. YUN Junhui. The steel rebar defect detection by using ultrasonic guided waves[D]. Dalian: Dalian University of Technology, 2013. [10] XU J, WU X, WANG L, et al. Detecting the flaws in prestressing strands using guided waves based on the magnetostrictive effect[J]. Insight-Non-Destructive Testing and Condition Monitoring, 2007, 49(11): 647-650. [11] 劉增華, 趙繼辰, 吳斌, 等. 高階縱向超聲導波在鋼絞線缺陷檢測中的應用研究[J]. 工程力學, 2011, 28(4): 214-220. LIU Zenghua, ZHAO Jichen, WU Bin, et al. Application study on defect detection in steel strands by using high-order ultrasonic longitudinal guided waves[J]. Engineering Mechanics, 2011, 28(4): 214-220. [12] 潘永東, 楊鋒, 張東波, 等. 斜拉索錨固區損傷的高階縱向導波檢測研究[J]. 橋梁建設, 2015, 45(4): 52-57. PAN Yongdong, YANG Feng, ZHANG Dongbo, et al. Research of technique of high-order longitudinal guided wave detection of damage in stay cable anchorage zone[J]. Bridge Construction, 2015, 45(4): 52-57. [13] 顏華, 彭珍. 基于互相關和插值運算的聲波飛行時間測量[J]. 沈陽工業大學學報, 2008, 30(6): 662-666. YAN Hua, PENG Zhen. Acoustic travel-time measurement based on cross-correlation and interpolation[J]. Journal of Shenyang University of Technology, 2008, 30(6): 662-666. Numerical simulation of ultrasonic guided wave detection for cable steel wire damage of suspension bridge ZHANG Dong-bo1,2, WANG Bo1,2, WANG Zheng-xing1,2, WANG Zi-yu1,2 (1. China Railway Bridge Science Research Institute, Ltd., Wuhan 430034, Hubei, China;2. State Key Laboratory for Health and Safety of Bridge Structures, Wuhan 430034, Hubei, China) Abstract: In order to effectively detect cable steel wire damage of long span suspension bridge, the ultrasonic guided wave nondestructive testing technique is investigated by combing theoretical analysis and numerical simulation in this paper. Guided wave dispersion curves in steel wires are obtained by theory to analyze the dispersion characteristics. The L(0, 1) model of the central frequency at 200kHz is selected for the damage detection of steel wires, and the finite element software is used for the comprehensive study of dispersion curves and wave structure. The low order guided wave modes in steel wire are identified by two dimensional Fourier transform technique. Meanwhile, the influence of defect size and angle on the defect reflection coefficient of L(0, 1) mode is analyzed. Finally, the defect signals at the broken positions of two and seven cable steel wires are simulated. The results of the numerical simulation are in good agreement with that of theoretical analysis, which indicates that the low frequency L(0, 1) mode can effectively detect the wire broken damage of cable wires over a long distance. Key words: suspension bridge; cable wire system; ultrasonic guided wave; dispersion characteristics; numerical simulation; damage detection 中圖分類號：TB559 文獻標識碼：A 文章編號：1000-3630(2019)-04-0395-08 DOI編碼：10.16300/j.cnki.1000-3630.2019.04.007 收稿日期: 2018-03-08; '修回日期: 2018-04-12 作者簡介:張東波(1985－), 男, 河南商丘人, 博士研究生, 研究方向為超聲無損檢測。 通訊作者: 張東波,E-mail: chinamath@163.com