基于雙歐拉法的魚雷空中彈道仿真

任 斌, 溫志文, 楊智棟

基于雙歐拉法的魚雷空中彈道仿真

任 斌1, 溫志文2, 楊智棟2

(1. 海裝裝備項目管理中心, 北京, 100071; 2. 中國船舶重工集團公司 第705研究所, 陜西 西安, 710077)

傳統(tǒng)魚雷彈道六自由度仿真多基于歐拉角方法求解運動微分方程, 可以直觀地得到魚雷的位置和姿態(tài)角。但隨著魚雷空投彈道的出現(xiàn), 在傾角±90°的情況下會產(chǎn)生奇異點, 致使歐拉方程無法求解, 得不到正確結(jié)果。為克服上述不足, 文中采用雙歐拉法建立魚雷運動數(shù)學模型, 并對魚雷空中彈道進行數(shù)值計算。仿真結(jié)果表明, 基于雙歐拉法的彈道模型能夠正確地反映魚雷空中彈道運動規(guī)律, 在計算過程中不會因出現(xiàn)奇異點而發(fā)散。

魚雷; 空中彈道; 雙歐拉法

0 引言

空投魚雷由于可以有效增加魚雷的航程和速度, 一直以來, 都受到各國海軍及相關(guān)研究機構(gòu)重視[1]。而歐拉角具有概念清晰、運用實現(xiàn)簡單的優(yōu)點, 因此通常情況采用歐拉方程來描述魚雷的六自由度運動方程[2]。

然而歐拉方程在描述魚雷運動方程有一個致命缺陷: 在魚雷俯仰角為±90°時, 由歐拉方程解算出來的偏航角和橫滾角會出現(xiàn)奇異, 無法得到正確的姿態(tài)角[3]。在進行空投魚雷研究時, 不可避免地會遇到魚雷俯仰角為±90°的情況, 因此研究此時魚雷姿態(tài)角的解算方法對魚雷彈道的研究具有重要意義[4]。

航空航天領(lǐng)域?qū)W拉方程奇異性的研究較早, 也有了比較充分的認知。通常采用四元數(shù)法和雙歐拉法這2種方法解決以上問題[5]。其中, 四元數(shù)法由于存在原理性缺陷, 在數(shù)值計算過程中會不斷累積計算誤差[6]。而雙歐拉法沒有原理性缺陷, 通過正、反歐拉方程的交替使用, 可有效解決單歐拉方程的奇異性問題[7], 所以得到了廣泛的應(yīng)用。

文中將雙歐拉法引入到空投魚雷的六自由度方程中, 以魚雷空中彈道為研究對象, 應(yīng)用雙歐拉法建立魚雷運動數(shù)學模型, 采用正反歐拉方程的交替使用, 對魚雷空中運動規(guī)律進行有效計算分析, 為魚雷空中彈道的研究提供支撐。

1 魚雷運動微分方程

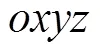
1.1 基于正歐拉變換的運動方程

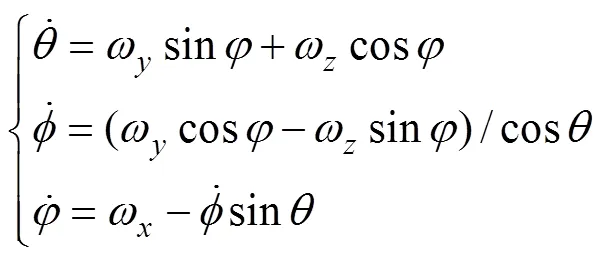
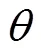
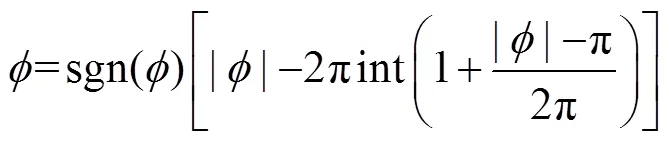
1.2 基于反歐拉變換的運動方程

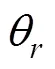
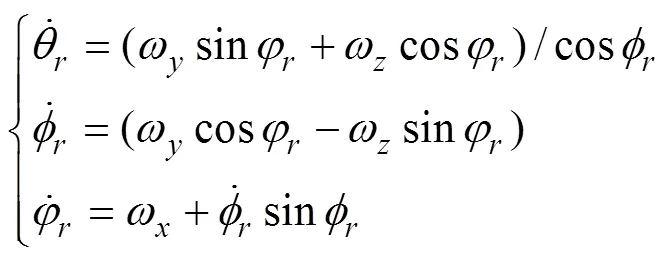
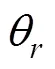
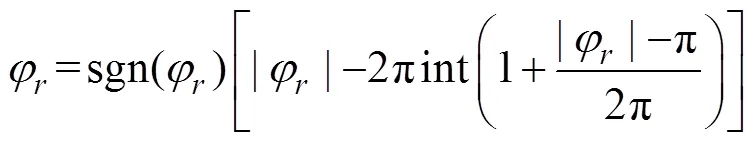
1.3 采用雙歐拉法克服雷傘系統(tǒng)歐拉方程奇異性

由式(1)和式(3)可知, 正歐拉方程俯仰角在±90°附近, 求解出現(xiàn)奇異性, 在0°(和180°)位置附近, 求解比較準確。與此相反, 反歐拉方程在0°(和180°)位置附近求解出現(xiàn)奇異性, 在±90°附近求解比較準確[8]。那么在求解魚雷空中運動方程時, 在±90°附近采用反歐拉方程進行計算, 在0°(和180°)位置附近采用正歐拉方程求解, 運用正反歐拉方程交替運行, 可得到比較精確的解[9]。

正反歐拉方程在交替運行時由于存在積分環(huán)節(jié), 所以在每次計算前都需要提供初始值, 這需要通過正反歐拉方程所對應(yīng)轉(zhuǎn)換矩陣的坐標轉(zhuǎn)換來實現(xiàn)。

用正歐拉角表示從地面坐標系到雷體坐標系的轉(zhuǎn)換矩陣

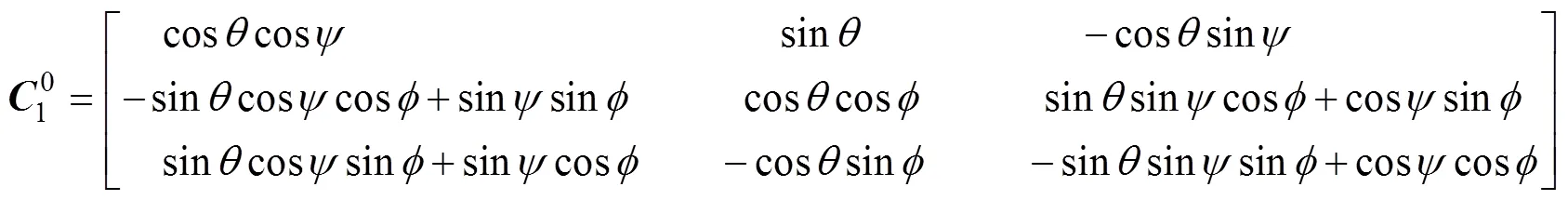
若用反歐拉角表示, 則為

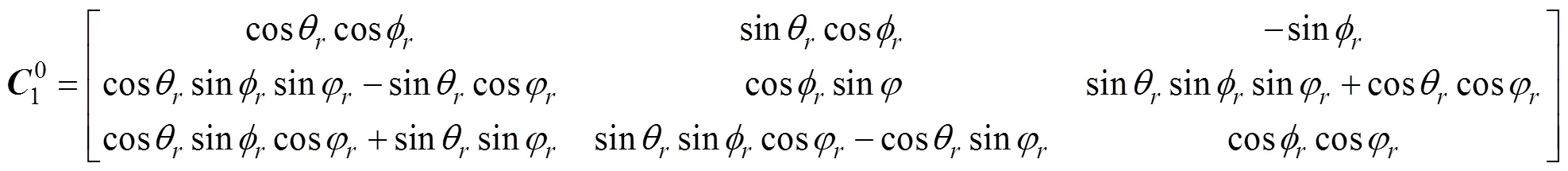
則兩轉(zhuǎn)換矩陣中對應(yīng)元素相等, 可得正歐拉角轉(zhuǎn)換為反歐拉角

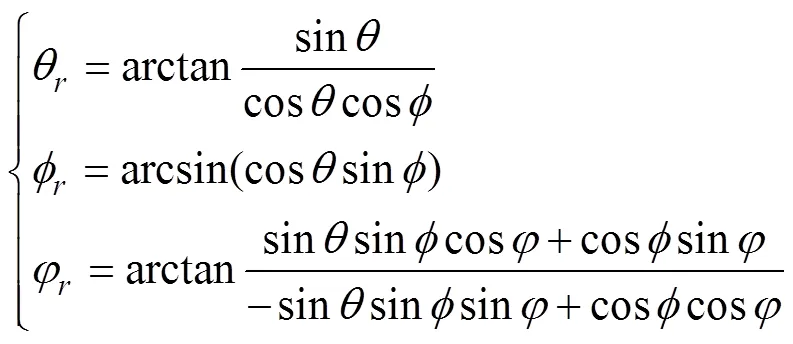
反歐拉角轉(zhuǎn)換為正歐拉角

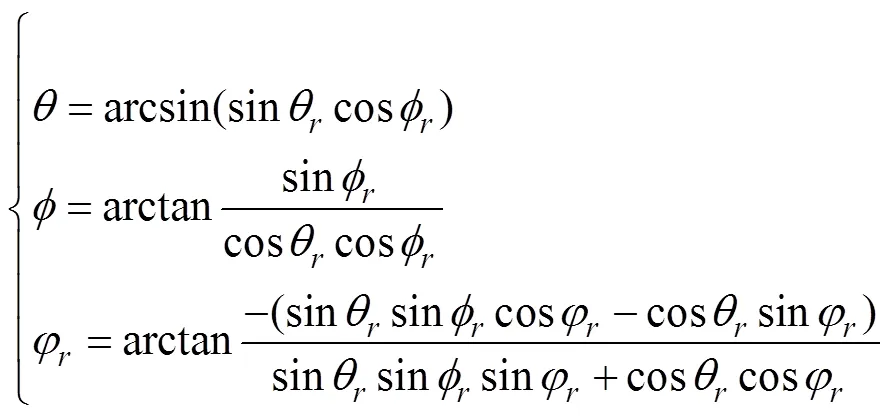
1.4 雙歐拉法求解流程

雙歐拉法求解流程圖如圖1所示。

2 仿真實例及分析

以某魚雷空投彈道為例, 魚雷質(zhì)量10 kg, 長度1 m, 初始彈道高度500 m, 初始速度v=10 m/s,v=150 m/s, 初始俯仰角90°。利用文中雙歐拉方法建立魚雷運動數(shù)學模型, 通過仿真得到該魚雷的空投彈道(見圖2)。

圖3為魚雷軸向運動曲線, 由圖可以看出, 魚雷的下落速度在3 s后接近穩(wěn)定值, 約在10 s時達到穩(wěn)定狀態(tài), 速度穩(wěn)定在29.4 m/s左右。圖4為魚雷俯仰角變化曲線, 由圖可知, 魚雷初始俯仰角為90°, 在降落傘的作用下翻轉(zhuǎn)(降落傘繩系于雷尾)。大約在10 s時達到穩(wěn)定狀態(tài), 俯仰角穩(wěn)定在–89.83°左右。

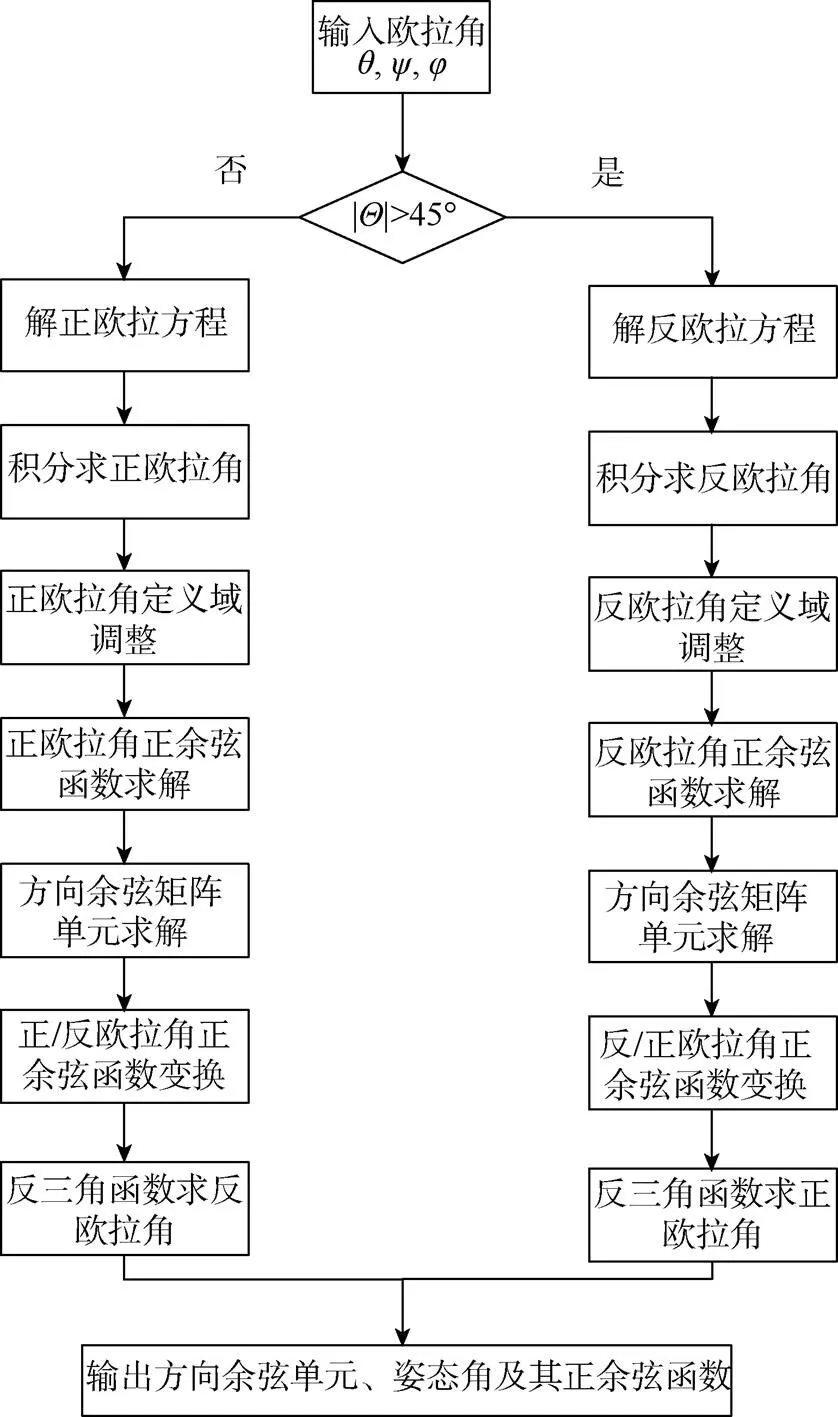
圖1 雙歐拉法運算流程

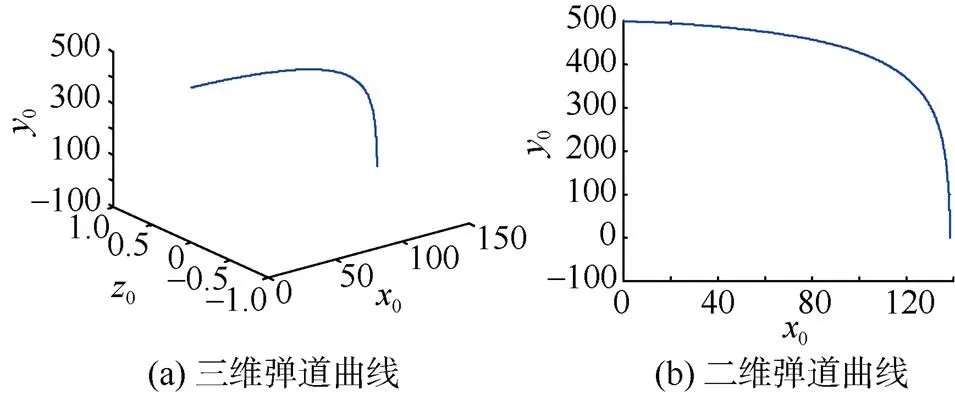
圖2 空投魚雷彈道曲線

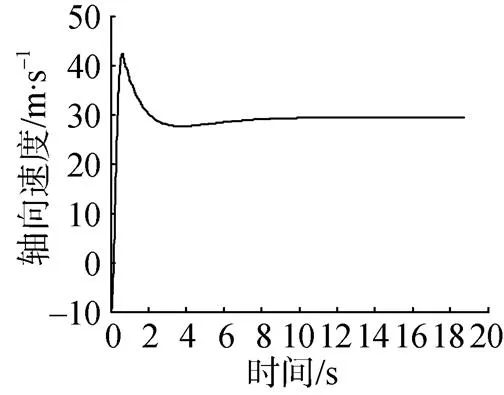
圖3 魚雷軸向速度曲線

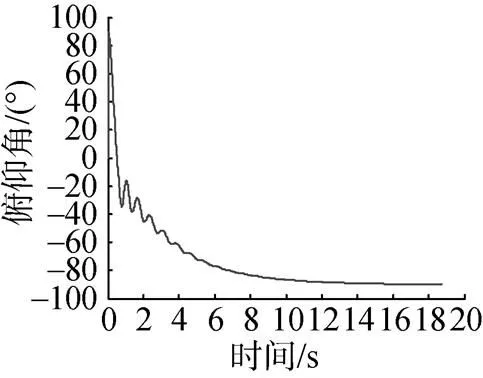
圖4 魚雷俯仰角變化曲線

由圖2~圖4可知, 文中采用的雙歐拉法可以較好地解決空投魚雷在俯仰角接近±90°時產(chǎn)生的奇異問題。

根據(jù)文中仿真結(jié)果與實際試驗數(shù)據(jù)對比(見表1)可得二者能夠保持一致, 證明了文中方法的可行性和準確性。

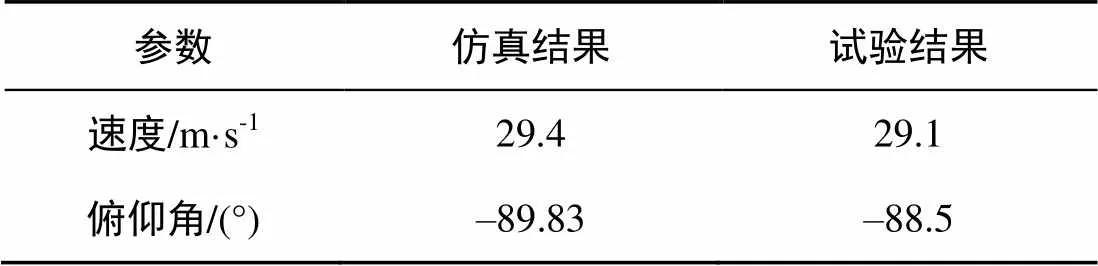
表1 文中仿真結(jié)果與實際試驗結(jié)果比較

3 結(jié)束語

空投魚雷在空中運動非常復雜, 姿態(tài)變化十分劇烈, 甚至可能發(fā)生大攻角翻轉(zhuǎn)的現(xiàn)象。為避免這種局限性, 采用雙歐拉法建立魚雷空中運動學方程, 并在大攻角條件下進行仿真計算, 結(jié)果表明: 基于雙歐拉法變換的彈道模型可正確反映空投魚雷的運動規(guī)律, 能夠仿真得到實際的彈道軌跡, 在計算過程中不會出現(xiàn)由于奇異點而導致方程退化的現(xiàn)象, 為魚雷大幅度姿態(tài)運動的空投彈道研究提供了理論參考。

[1] 曲延明, 周明, 林宗祥. 基于Simulink的飛航式火箭助飛魚雷空中彈道仿真[J]. 艦船科學技術(shù), 2011, 33(12): 107-111.Qu Yan-ming, Zhou Ming, Lin Zong-xiang. Research on Air Trajectory Simulation of the Cruising Rocket Assisted Torpedo Based on Simulink[J]. Ship Science and Tech- nology, 2011, 33(12): 107-111.

[2] 李躍軍, 閻超. 飛行器姿態(tài)角解算的全角度雙歐拉法[J]. 北京航空航天大學學報, 2007, 33(5): 505-508.Li Yue-jun, Yan Chao. Improvement of Dual-Euler Me- thod for Full Scale Eulerian Angles Solution of Aircraft[J]. Journal of Beijing University of Aeronautics and Astro- nautics, 2007, 33(5): 505-508.

[3] 周明, 徐德民. 火箭助飛魚雷彈道的仿真實現(xiàn)與應(yīng)用研究[J]. 彈箭與制導學報, 2007, 27(2): 235-238.Zhou Ming, Xu De-min. Infection of Impact Dispersion to the Rocket Assisted Torpedo Detection Probability[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2007, 27(2): 235-238.

[4] 王亞東, 袁緒龍, 張宇文. 雙歐控制法在運載器水彈道中的應(yīng)用[J]. 魚雷技術(shù), 2013, 11(6): 401-405.Wang Ya-dong, Yuan Xu-long, Zhang Yu-wen. Appli- cation of Dual-Euler Control Method to Water-Trajectory Design of Missile Carrier[J]. Torpedo Technology, 2013, 11(6): 401-405.

[5] 杜陽華, 吳宇. 火箭助飛魚雷發(fā)控及彈道仿真[J]. 指揮控制與仿真, 2014, 36(3): 89-94.Du Yang-hua, Wu Yu. Rocket-assisted Torpedo Fire Con- trol and Ballistic Trajectory Simulation[J]. Command Control & Simulation, 2014, 36(3): 89-94.

[6] 王曉娟, 唐世軒, 劉正平. 火箭助飛魚雷系統(tǒng)建模與空中彈道仿真研究[J]. 彈箭與制導學報, 2003, 23(2): 51-55.Wang Xiao-juan, Tang Shi-xuan, Liu Zheng-ping. The Rocket-Assisted Torpedo System to Set Up the Mold and Air the Trajectory to Imitate the True Research[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2003, 23(2): 51-55.

[7] Jia Y, Song B W, Liang Q W, et al. Simulation of Trail Gui- dance Trajectory of a Model Torpedo Based on MATLAB/ Simulink[J]. Systems Engineering-Theory & Practice, 2006, 26(3): 141-140.

[8] 周偉, 張曉今, 寇保華, 等. 雙歐拉法在克服傘-彈系統(tǒng)歐拉方程奇異性中的應(yīng)用[J]. 航天返回與遙感, 2003, 24(3): 4-8.Zhou Wei, Zhang Xiao-jin, Kou Bao-hua, et al. The Application of the Dual-euler Method for Overcoming the Singularity of Euler Equation in Parachute-Missile System[J]. Spacecrafts Recovery & Remote Sensing, 2003, 24(3): 4-8.

[9] 岳軍紅, 賀懷清. 克服歐拉方程奇異性的方法[C]//第六屆全國交通運輸領(lǐng)域青年學術(shù)會議論文集. 大連: 第六屆全國交通運輸領(lǐng)域青年學術(shù)會議, 2005.

Simulation of Torpedo Air Trajectory Based on Dual-Euler Method

REN Bin1, WEN Zhi-wen2, YANG Zhi-dong2

(1. Armament Project Management Center of Naval Equipment Department, Beijing 100071, China; 2. The 705 Research Institute, China Shipbuilding Industry Corporation, Xi’an 710077, China)

Due to its advantages of obtaining torpedo’s attitude angle and position intuitively, Euler angle representation has been extensively applied to solve the differential equation of torpedo’s six-DOF motion. However, for the torpedo air trajectory, this representation will produce singular points at the pitching angles of ± 90°, leading to the fact that the Euler equation cannot be solved. Therefore, this paper employs the dual-Euler method to avoid such singularity. Based on the dual-Euler method, a mathematical model of torpedo motion is established, and the torpedo air trajectory is numerically simulated. There is no divergence induced by the singularity during the calculation process. Simulations result shows that the torpedo air trajectory model based on the dual-Euler method can reflect the motion characteristics of torpedo air trajectory, and can achieve satisfactory performance at arbitrary angles. This work may provide a theoretical reference for the study of torpedo air trajectory.

torpedo; air trajectory; dual-Euler method

TJ631.7; O351.2

A

2096-3920(2019)04-0459-04

10.11993/j.issn.2096-3920.2019.04.015

任斌, 溫志文, 楊智棟. 基于雙歐拉法的魚雷空中彈道仿真[J]. 水下無人系統(tǒng)學報, 2019, 27(4): 459-462.

2018-11-11;

2019-01-06.

任 斌(1982-), 男, 碩士, 主要研究方向為水中兵器裝備管理.

(責任編輯: 陳 曦)