南水北調工程某標段GPS高程線性擬合改進方法研究
孟俊貞,馬開鋒, 黃桂平,趙繼偉,楊衛森
(1. 華北水利水電大學 地球科學與工程學院,河南 鄭州 450046;2. 華北水利水電大學 測繪與地理信息學院,河南 鄭州 450046;3. 華北水利水電大學 水利學院,河南 鄭州 450046)
0 引 言
GPS測量技術能夠快速獲取高精度的三維測量數據,是控制測量的首選方法. 但GPS測量結果只能給出相對于WGS-84橢球的大地高,不能直接應用于我國測繪生產與工程建設中所采用的正常高系統中,為此需要進行GPS高程的擬合轉換. 近年來,許多學者進行了GPS高程擬合方面的研究[1-17],獲得了豐富的理論與實踐經驗. 但當GPS控制網線形布設時,即可采用解析內插的方法進行確定待定點的正常高,即通過已知高程控制點的平面坐標與高程異常值,由構造的插值函數擬合測線方向上的似大地水準面曲線,然后內插其它點的高程異常值[8,12-13]. 比較經典的解析內插法主要有:多項式曲線擬合法、正交函數曲線擬合法、三次樣條曲線擬合法與Akima曲線擬合法等. 每種方法各有特點、各具優勢. 其中多項式曲線擬合法,雖然計算比較簡單,但當存在較多擬合點采用最小二乘原理計算時,常常出現系數矩陣病態,使得擬合效果不理想. 故本文重點針對正交函數曲線擬合法、三次樣條曲線擬合法與Akima曲線擬合法及其改進優化進行研究.
1 GPS高程線性擬合方法
1.1 正交函數曲線擬合法
GPS高程線性擬合方法中有常見的多項式擬合方法,但多項式擬合方法在用最小二乘法解算時,得到的系數矩陣常常是病態的,為了避免求解這種病態方程組,通常利用正交函數(函數向量內積為零的函數)來確定擬合多項式[13].
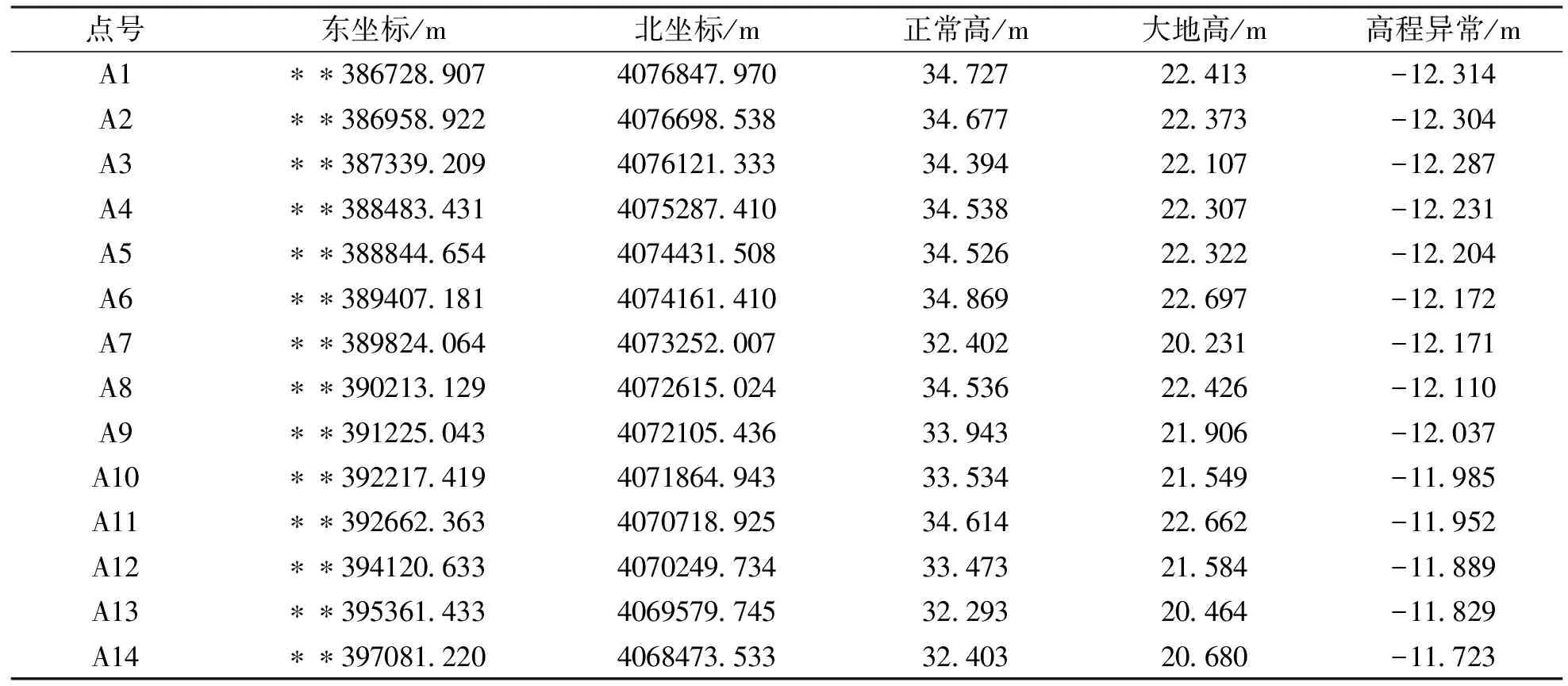
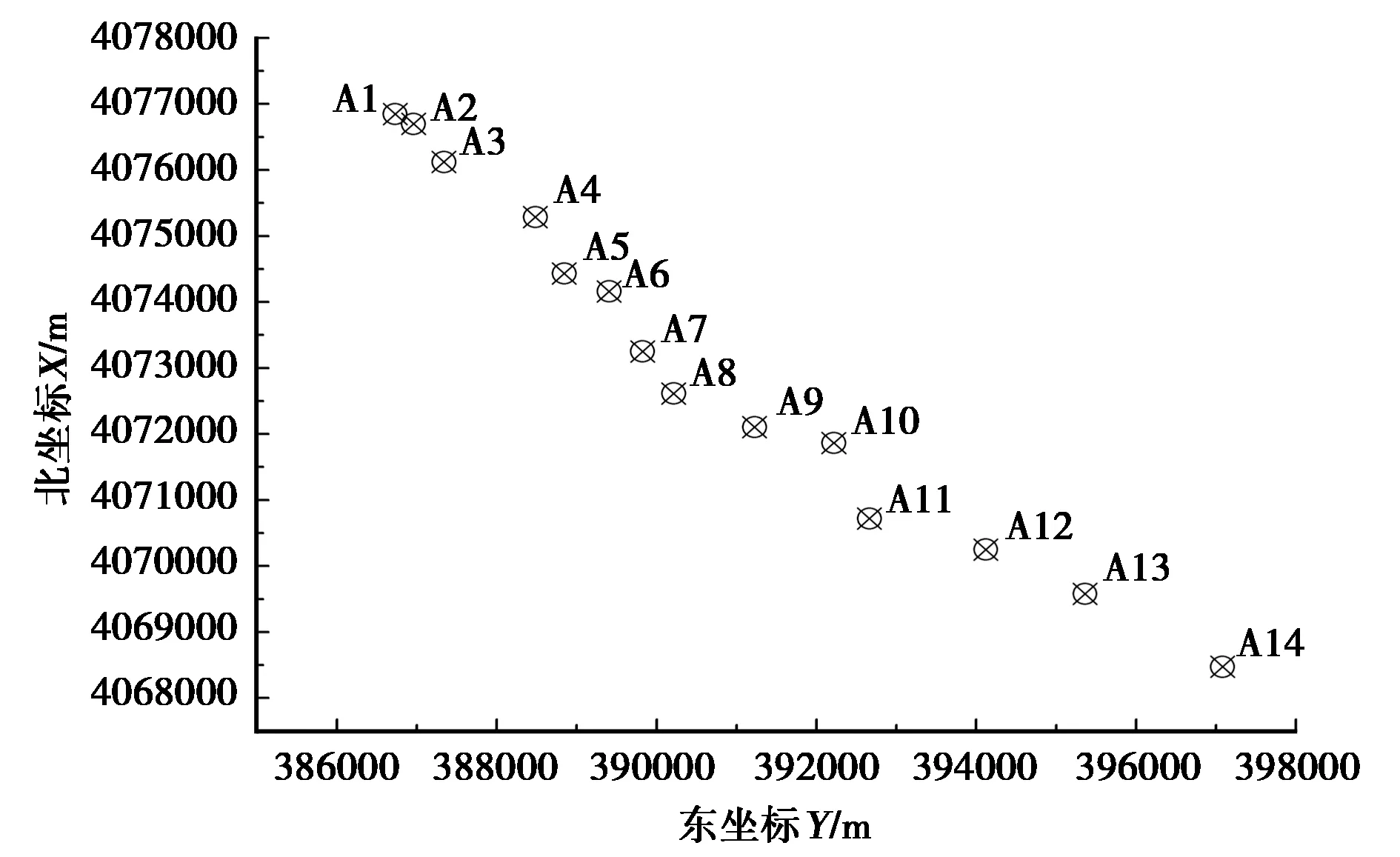
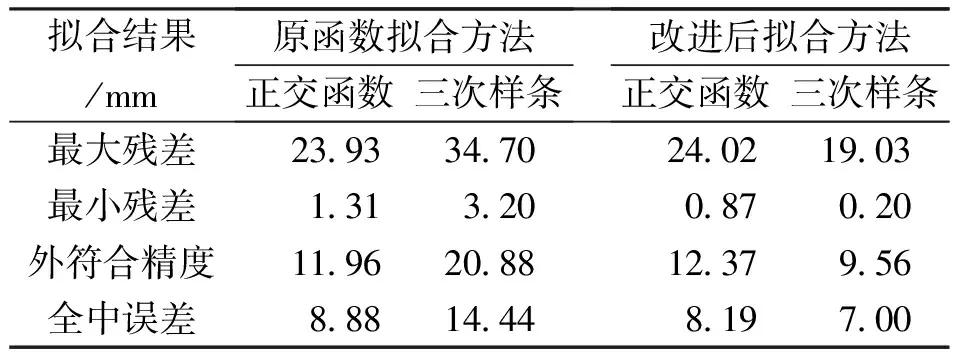
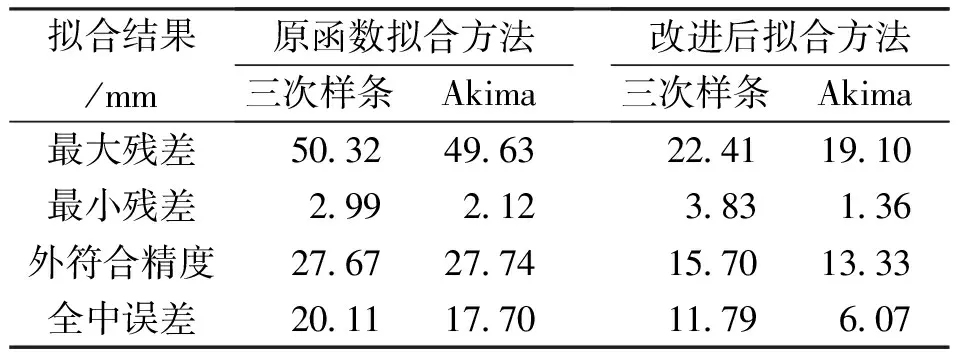
設給定n+1個數據點(xi,ξi)(i=0, 1, 2, …,n),需要確定一個m次的最小二乘擬合多項式(其中m (1) 式中,a0,a1,…,am為多項式系數. 若能夠構造出一組次數不超過m的在給定點上的正交多項式Qj(x)(j=0,1,2,…,m),則可以首先用Qj(x)作為基函數,進行最小二乘擬合,即: Pm(x)=q0Q0(x)+q1Q1(x)+…+ qmQm(x), (2) 式中,系數qj(j=0,1,2,…,m)為 (3) 然后將各個qj代入式(2),并展開成一般多項式(1). 構造給定點上的正交多項式Qj(x)(j=0,1,2,…,m)的遞推公式如下: (4) 其中: (5) (6) 其中: (7) 在實際計算中,可以根據遞推公式(4)逐步求出各正交多項式Qj(x),并用公式(3)計算出組合系數qj. 同時,逐步將每次計算得到的qjQj(x)項展開后累加到擬合多項式(1)中,得到m次的擬合多項式. 將待求點的擬合坐標代入,即可求出其高程異常[13]. 在測線較長、己知點較多、高程異常變化較大時,按最小二乘原理求得的多項式系數削高補低的誤差會增大. 為避免高次插值引起的振蕩現象以及分段低次插值連接點上的不光滑性,通常采用以三次樣條函數作為擬合模型的分段計算方式. 三次樣條曲線實際上是由多段三次多項式曲線拼接而成的連續曲線.在段間連接點處,不僅函數自身連續,且其一階導數和二階導數也是連續的.這樣不僅克服了單個多項式不靈活、不穩定的缺點,而且保留了多項式的表達與計算的簡便性,因而在較長測線GPS高程擬合中得到了較為廣泛的應用. ξ(x)=ξ(xi)+(x-xi)ξ(xi,xi+1)+ (x-xi)(x-xi+1)ξ(x,xi,xi+1), (8) ξ″(xi)(i=1,2,…,n-1)滿足系數矩陣為對稱三角陣的線性方程組: (9) 用追趕法求解方程組(9),可求出ξ″(xi),而 ξ″(x)=ξ″(xi)+(x-xi)ξ″(xi,xi+1). (10) 利用二階差商與式(10),可求得ξ(x,xi,xi+1),再將ξ(x,xi,xi+1)代入式(8),即可求得待定點的高程異常擬合值. 該方法是指在兩個已知點間內插時,除用這兩個己知點外,還需用兩己知點外的兩個點,其目的是使函數曲線光滑、連續. 設有6個已知點(i=1, 2, …, 6),現需要在3號點和4號點之間內插任一待求點,其計算公式為 ξ(x)=P0+P1(x-x3)+P2(x-x3)2+ P3(x-x3)3. (11) 式中: (12) 式(12)中的t3、t4為3號點和4號點實測要素的斜率,t3用1~5號已知點計算,t4用2~6號已知點計算,一般計算公式為 (13) 式中,mi=(ξi+1-ξi)/(xi+1-xi). 當式(13)中分母為零時,ti=1/2(mi-1-mi)或ti=mi. 在進行上述正交函數、三次樣條、Akima等曲線擬合過程中,由于用于曲線擬合的已知點與檢核點不可能嚴格分布在一條直線上,故根據已知點與基準點之間的距離來求某一點的擬合坐標,顯然是不夠準確的,為了改善曲線擬合的精度,在已有曲線擬合方法的基礎上,進行了曲線擬合坐標算法的改進優化. 假定曲線上第一個已知點的擬合坐標為0,則其中一個點的擬合坐標xi為該點與前一點的距離ri,i-1再加上前一點的擬合坐標xi-1,公式可表示為 xi=xi-1+ri,i-1. (14) 為了客觀評定GPS高程擬合計算的精度,通常在布設幾何水準聯測點時,在其施測區域內適當多聯測幾個GPS點,作外部檢核用. 所以,在評定GPS水準擬合精度時,一般主要采用外符合精度與每千米水準測量全中誤差兩個評價指標. (15) 2)每千米水準測量全中誤差Mw各相鄰檢核點高差較差DVh可看作是符合水準路線的閉合差,如此可計算出每千米水準測量全中誤差Mw,具體計算公式如下: (16) 式中:N為高差個數;F為比較高差的檢核點間距離,km. 南水北調工程某標段已測量的GPS點位數據和四等水準數據結果,如表1所示. 其點位位置分布如圖1所示. 表1 已測數據結果 圖1 點位分布圖 由圖1可知,該區域所測點位呈線性分布,故較適合于采用GPS線性擬合方法進行高程異常擬合. 為驗證文中所提改進方法的有效性,分別采用正交函數、三次樣條與Akima曲線模型對其進行高程擬合,并采用外符合精度M與全中誤差Mw進行擬合精度比較分析. 方案一:對正交函數(此處采用三階函數)與三次樣條曲線擬合進行驗證,此處選取A1、A4、A6、A7、A8、A9、A12、A14這8個點來計算擬合模型參數,其余點作為檢核點進行擬合殘差計算及精度結果評定,如表2所示. 方案二:對三次樣條與Akima曲線擬合進行驗證,此處選取A1、A2、A3、A5、A7、A9、A12、A13、A14這9個點來計算擬合模型參數,其余點作為檢核點進行擬合殘差計算及精度結果評定,如表3所示. 表2 方案一擬合結果 表3 方案二擬合結果 表2結果表明,采用原正交函數與三次樣條曲線擬合方法時,針對此選點方案原正交函數與三次樣條曲線擬合方法得到的結果,其全中誤差分別達到了8.88 mm與14.44 mm,很明顯正交函數曲線擬合方法的精度結果較好. 而通過兩者改進后的方法分別進行擬合計算可知,改進后的正交函數與三次樣條曲線擬合方法擬合結果精度的全中誤差均有提升;但改進后的正交函數擬合結果中,其最大殘差與外符合精度還有所變大,這是由于計算其模型參數時所選點位的非線性組合方案導致的;而改進后的三次樣條曲線擬合結果的精度有明顯改善,其精度提高了一倍,全中誤差達到了7.00 mm,從而顯示了改進后三次樣條曲線擬合方法針對此選點方案的優越性. 表3結果表明,采用原三次樣條與Akima曲線擬合方法時,針對此選點方案三次樣條與Akima曲線擬合方法得到的結果,其全中誤差分別達到了20.11 mm與17.70 mm,相對來說Akima曲線擬合方法的精度結果較好. 而通過兩者改進后的方法分別進行擬合計算可知,改進后的三次樣條與Akima曲線擬合方法擬合結果精度均有明顯提升,其中改進后的三次樣條曲線擬合結果的精度提高了近一倍,全中誤差達到了11.79 mm,改進后的Akima曲線擬合方法擬合結果的精度提高了近兩倍,全中誤差達到了6.07 mm,從而顯示出了改進后的Akima曲線擬合方法針對此選點方案的明顯優越性. 通過總體分析,在選點適宜的情況下,采用改進后的Akima曲線擬合方法能夠對線性區域的GPS高程異常進行較高精度的擬合計算,可以作為GPS高程線性擬合的首選方法. 本文方法主要針對相對較為線性的區域進行了數據測試驗證,若擬合區域存在較大弧段時,本文方法是否有效,還需進一步測試研究. 通過分別采用原正交函數、三次樣條與Akima曲線擬合方法與分別改進后的擬合方法對南水北調工程某標段的GPS高程線性擬合,得到了針對不同的選點方案,同一種擬合方法也有不同的擬合精度結果;針對同一種選點方案,不同的擬合方法也有不同的擬合精度結果;而對于文中所提的改進后的曲線擬合方法均有不同程度的精度提升,其中改進后的Akima曲線擬合方法的擬合精度結果提升最為明顯,故針對線性擬合區域在選點適宜的情況下,可以考慮采用改進后的Akima曲線擬合方法對其GPS高程異常進行較高精度的擬合計算,從而獲得較理想的高精度擬合結果.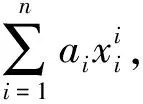
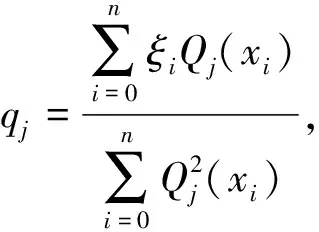
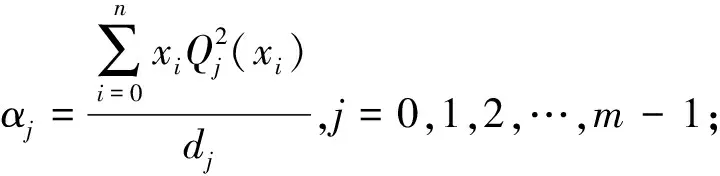
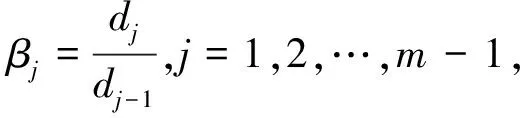
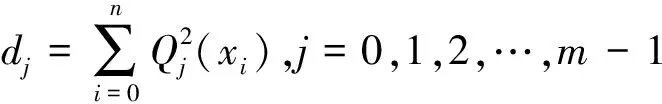
1.2 三次樣條曲線擬合法
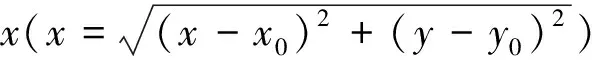
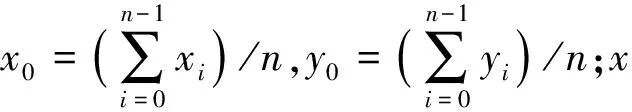
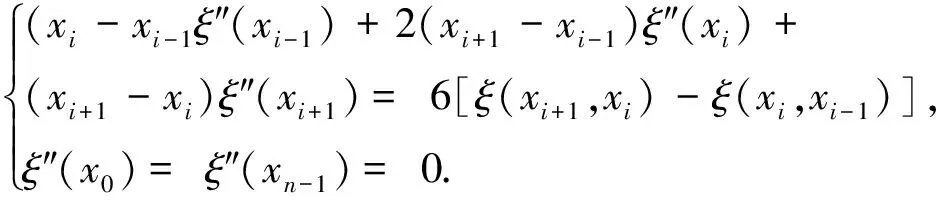
1.3 Akima曲線擬合法
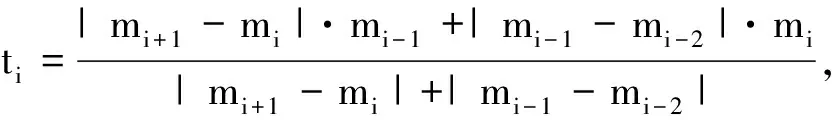
2 GPS高程線性擬合改進方法及精度評定
2.1 GPS高程線性擬合改進方法
2.2 精度評定
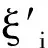
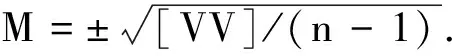
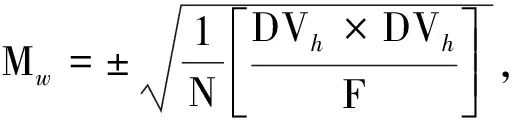
3 實例應用
4 結束語

