基于Isight的傾轉旋翼飛行器前飛狀態翼型優化

趙廣，何國毅，王琦，羅云，王振

(南昌航空大學 飛行器工程學院，南昌 330063)

0 引 言

傾轉旋翼飛行器不僅具有直升機的垂直起降(VTOL)能力，同時擁有固定翼飛機的高速、長航程特點，被認為是下一代旋翼類飛行器的主要發展方向[1]。機翼作為飛行器的核心部件，其設計很大程度上決定了飛行器的性能。開展對傾轉旋翼飛行器機翼的氣動優化設計，對于提高傾轉旋翼飛行器飛行性能具有重要意義。

目前，國內外已在傾轉旋翼飛行器的優化方面做了大量研究。國外，L.Vigevano等[2]總結了NICETRIP項目進行的傾轉旋翼飛行器ERICA的氣動特性分析和一些部件(例如機身/機翼整流罩、機翼等)的優化設計，在對機翼進行優化時，根據旋翼滑流的影響，將機翼分為固定段(層流翼型)和傾轉段(湍流翼型)，認為同時結合兩種翼型的機翼可實現明顯的減阻效果，但未指出具體的優化過程；M.K.Lee等[3]和R.L.T.Bevan等[4]通過在機翼上安裝一些附屬裝置提高飛行性能，例如在發動機短艙外再增加一小段機翼，雖然機身重量略微增加，但機翼升阻比卻得以顯著提高，或者在機翼上安裝渦流發生器，與干凈機翼相比，可在減阻的同時減少氣流分離；M.Kim等[5]采用主動控制的方法，懸停模式在前緣和后緣同時使用射流，可減少機翼所受下洗載荷；傾轉模式只需在前緣使用射流，可使阻力明顯減小。

國內，針對傾轉旋翼飛行器的機翼優化的研究主要有：徐家寬等[6]、孫凱軍等[7]指出處在滑流影響下的機翼等部件與無滑流影響區域的流場特征不同，螺旋槳滑流會對機翼升阻特性產生顯著影響。王科雷等[8]認為機翼優化時不考慮滑流影響，實際工作狀態與設計點存在偏離，導致氣動特性得不到提升。朱秋嫻等[9]根據前飛狀態下旋翼/機身/短艙對機翼影響沿展向的分布，將機翼分成三段，在每段取特征剖面采用代理模型進行優化，優化后全機升阻比增大了36.78%，但優化細節未給出。

綜上，目前對于傾轉旋翼飛行器機翼優化方面涉及具體方法的研究仍較少。本文在前人研究的基礎上，根據“由于旋翼存在，導致前飛時機翼展向位置氣動環境不同”這一實際，將機翼分為內外兩段，在每段選取代表性截面，并選擇截面上的速度表征兩段機翼氣動環境的不同，優化前飛狀態兩段機翼翼型；通過對比兩種速度設定的優化效果，以期為傾轉旋翼飛行器的氣動布局設計提供一些有參考意義的結論。

1 流場求解方法

在直角坐標系下求解帶有動量源項的RANS方程：

(1)

其中，

式中：ρ、p、E、H分別為氣體的密度、壓強、總能和總焓；V=[u,v,w]T為氣體的絕對速度；J為動量源項。

2 動量源方法及驗證

由于精確求解旋翼需要在槳葉幾何上生成貼體網格，會導致網格數目過大，耗費大量的計算資源。采用動量源方法時，旋翼用作用盤代替，槳葉對氣流的作用以動量源代替。可大幅降低網格數量，提高計算效率。

作用盤即在旋翼葉片掃過的區域由一些有限厚度的網格組成。動量源即在作用盤區域每個網格中引入表示葉片對周圍氣體的作用力。作用盤方向對應實際的旋翼槳盤方向。作用盤半徑對應實際槳葉半徑。動量源S可表示為

(2)

式中：Nb為槳葉數量；F為槳葉微段所受的氣動力，其計算基于葉素理論；Δτ為槳葉掃過該網格單元時所轉過的角度；Vcell為網格單元的體積。

為了驗證動量源的計算精度，計算文獻[10]的算例，對比結果如圖1所示，圖1(a)和圖1(b)分別為槳盤下方不同位置處的動壓對比。

(a)y=0.215R

(b)y=0.660R圖1 旋翼下方動壓分布與實驗的對比Fig.1 Comparison of the dynamic pressure distribution under rotor with experiment

從圖1可以看出：動量源結果與文獻的實驗值趨勢一致，且結果較為接近，因為本文選取旋翼后方代表性截面的速度分布做優化，此算例表明動量源方法可以較為準確地模擬旋翼下方的動壓(速度)分布。

3 物理模型及準確性驗證

3.1 物理模型

本文在傾轉旋翼飛行器前飛狀態下進行優化，為了減小計算量，采用半翼展模型，如圖2所示，旋翼用作用盤(Actuator Disk)代替。

圖2 傾轉旋翼飛行器半翼展模型Fig.2 Half wingspan model of tiltrotor aircraft

由于旋翼的影響，機翼可分為內側機翼(Inner Wing)自由來流區和外側機翼(Outer Wing)旋翼尾流區[11]，如圖3所示。旋翼半徑和兩段機翼展長均為R。優化前兩段機翼翼型均為NACA2412。

圖3 傾轉旋翼飛行器機翼優化截面的選取Fig.3 Optimization section selection of the wing of tiltrotor aircraft

根據兩段機翼所處來流速度的不同，取每段機翼的代表性截面，對二維翼型NACA2412進行優化，分別得到翼型Arifoil 1、Airfoil 2，再將優化后的翼型各自拉伸成內側機翼和外側機翼。因為槳葉的0.7R處特征剖面的空氣動力學特性具有代表性[12]，對于外側機翼，取槳葉上此特征剖面對應在機翼上的位置為代表性截面，即圖3所示的0.7R。對于內側機翼，可視為處于自由來流中，可取機翼中段為代表性截面，即圖3中的0.8R。

本文在V∞=15 m/s，旋翼前進比λ=0.1(λ=V∞/(Ω×R)，Ω為旋翼角速度)，機翼攻角α=0°的工況下優化的，以升阻比K最大為優化目標。優化前需先得出Arifoil 1、Airfoil 2的升力和阻力值。為了說明本文所用方法的有效性，采用兩種速度設定優化。設定一：優化時不考慮旋翼的影響，內側機翼和外側機翼翼型入口邊界速度均為15 m/s；設定二：優化時考慮旋翼的影響，內側機翼翼型入口邊界速度為15 m/s，外側機翼翼型入口邊界速度根據槳盤后方實際氣流速度，采用大小隨位置變化的非均勻來流，如圖4所示。計算域y方向大小根據徑向0.7R處所取截面在槳盤上對應的實際長度確定，如圖5所示。這兩種設定的區別在于對外側機翼翼型優化時邊界條件的選擇。

圖4 外側機翼入口速度分布Fig.4 Outer wing inlet velocity distribution

圖5 外側機翼計算域網格Fig.5 Outer wing computational domain mesh

3.2 計算精度驗證

對二維翼型優化前，需計算翼型的升阻力系數。根據文獻[13]提供的NACA4418翼型實驗數據，進行模擬計算。不同攻角下翼型升阻力系數與實驗值的對比如圖6所示，可以看出：計算值與實驗值較為吻合。

圖6 計算精度驗證Fig.6 Verification of computational accuracy

3.3 網格無關性驗證

為了排除網格對優化結果的影響，計算四套網格，網格數分別為Mesh1(110萬)、Mesh2(142萬)、Mesh3(175萬)和Mesh4(202萬)。網格定義和分布如圖7和表1所示，其中Ex、Ez分別為機翼弦向和展向邊上的節點數，Δs為邊界層第一層網格高度。

圖7 機翼幾何網格節點定義Fig.7 Definition of wing geometric mesh node

表1 四套網格的網格分布Table 1 Distribution of four sets of meshes

四套網格的計算結果如圖8所示。

圖8 四套網格升力、阻力計算結果Fig.8 Four sets of grid lift and drag calculation

從圖8可以看出：當網格數增加到175萬時，升力和阻力的波動已經很小，可認為計算結果幾乎不隨網格數目的變化而變化。為了兼顧計算精度和計算代價，本文選取Mesh3(175萬)網格計算。

4 翼型幾何參數化

在對翼型進行優化設計時，直接改變的是控制翼型生成的參數，進而實現翼型形狀更新。因此必須進行翼型參數化描述。

考慮到Hicks-Henne型函數方法應用廣泛，具有描述翼型精確、曲線平滑的優點[14]，本文采用以Hicks-Henne 為型函數的線性擾動法，即新翼型的幾何形狀由原始翼型和擾動的線性疊加來表示。

(3)

式中：yup、ylow分別為新翼型的上下翼面函數；yup0、ylow0分別為原始翼型的上下翼面函數；h為控制翼型生成的設計變量的個數。

理論上，設計變量h的個數越多，設計空間越大，但同時計算量也會極大增加，通常單個翼面h=4～9為宜[14]。本文取h=6，即翼型上下翼面各有6個設計變量用于改變翼型形狀。以型函數fh(x)的系數ah、ah+6(h分別為1,2,3,4,5,6)表示上下翼面控制翼型形狀的設計變量。ah的取值范圍為[-0.01 ,0.05]，ah+6的取值范圍為[-0.05,0.01]。

采用改進的Hicks-Henne型函數fh(x)[15]。

(4)

式中：e(h)=ln0.5/lnxh。

取xh(h分別為1,2,3,4,5,6)分別為0.15,0.30,0.45,0.60,0.75,0.90。

Hicks-Henne方法得到的翼型曲線如圖9所示。A1、A2為設計變量ah組成的向量。其中A1=[0,0,0,0.05,0.05,0.05,0,0,0,-0.05,-0.05,-0.05]T,A2=[0.05,0.05,0.05,0,0,0,-0.05,-0.05,-0.05,0,0,0]T。

圖9 Hicks-Henne 方法得到的翼型曲線Fig.9 Airfoil curves generated by Hicks-Henne method

從圖9可以看出：三組翼面曲線連續平滑，即使在翼型前緣和后緣均有較大的擾動量，表明采用改進的Hicks-Henne型函數能夠滿足對翼型參數化的要求。

5 基于Isight的優化設計流程

Isight優化流程如圖10所示，采用Isight優化平臺集成翼型幾何生成(MATLAB 程序)、網格劃分(Pointwise)和流場求解(Fluent)等軟件，實現翼型自動優化。

圖10 Isight優化流程Fig.10 Isight optimization process

代理模型的創建主要包括樣本數據采集和代理模型的選擇。本文采用最優拉丁超立方設計(Opt LHD)方法生成300個樣本點構造模型，另用115個樣本點用于誤差分析，對升阻比K建立代理模型。代理模型選RBF模型，該模型的優點是具有較強的擬合復雜非線性函數的能力。RBF代理模型精度分析如表2所示。

表2 RBF代理模型精度分析Table 2 RBF precision analysis of surrogate model

代理模型生成后一定要查看可信度，一般要求均方根誤差RSME小于0.2，相關系數R2大于0.9[16]。從表2可以看出：RSME小于0.2，且R2值較為接近0.9，因此認為建立的代理模型具有較高的可信度，可代替數值仿真實現優化。

優化組件采用多島遺傳算法(MIGA)，子群規模為10，島(子群)個數為10，總進化代數為10。

6 翼型優化結果及分析

對于外側機翼，由于優化時采用的邊界條件不同，即使是同一目標函數，優化后得到的翼型氣動外形也不同。優化后的外側機翼如圖11所示，可以看出：與原始翼型NACA2412對比，采用設定一得到的外側機翼優化翼型明顯變厚，翼型后半段下翼面上凸；設定二得到的外側機翼優化翼型彎度明顯增大，厚度與原始翼型相比略有減少。

圖11 外側機翼優化翼型與原始翼型的對比Fig.11 Comparison of optimized airfoil and original airfoil of outer wing

外側機翼翼型壓力云圖如圖12所示，可以看出：翼型上翼面上凸帶來了更大的低壓區；并且優化后的翼型下翼面上凸部分出現高壓區，有利于提高升力系數。采用兩種速度設定優化的翼型彎度都比原始翼型更大，翼型彎度變大增大了翼型的有效攻角，增加了升力系數。

(a)原始翼型

(b)速度設定一

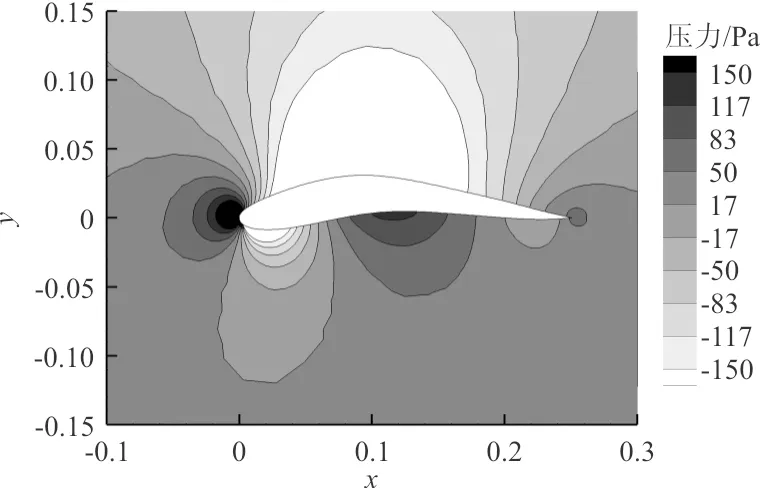
(c)速度設定二圖12 外側機翼翼型的壓力分布Fig.12 Pressure distribution of outer wing airfoil

將優化后的翼型應用到三維機翼上，優化前后氣動性能對比如表3所示。

表3 優化前后傾轉旋翼飛行器氣動性能對比Table 3 Aerodynamic performance comparison of tiltrotor aircraft before and after optimization

從表3可以看出：兩種速度設定雖然優化后阻力系數增大，但升力系數增加幅度更大，都能提高機翼的升阻比；對比兩種速度設定，設定二優化的翼型生成的三維機翼升力系數與設定一相當，但阻力系數更小。

上述優化結果是在攻角α為0°時得到的。傾轉旋翼機前飛時有不同的飛行狀態，因此本文計算攻角從0°～ 7°范圍內優化前后機翼的升阻比，如圖13所示。

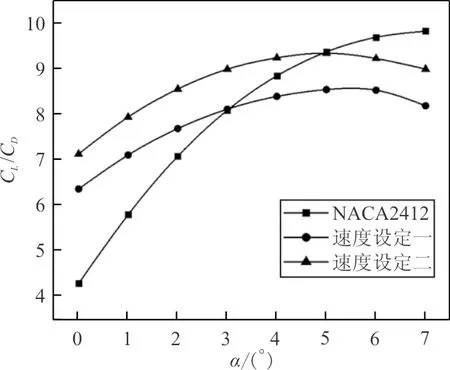
圖13 傾轉旋翼飛行器機翼升阻比優化前后對比Fig.13 Comparison of lift drag ratio of wing before and after optimization of tiltrotor aircraft

從圖13可以看出：在有限的攻角范圍內,兩種速度設定均能起到優化作用，對升阻比的提升率隨攻角增大而減小，且設定二的優化效果好于設定一；對于速度設定二，當攻角小于5°時，對升阻比有提升作用；而對于速度設定一，當攻角大于3°時，已經不能提高機翼升阻比。

7 結 論

(1)優化后的機翼升阻比提高，表明本文建立的基于Isight自動優化平臺及代理模型的方法適用于傾轉旋翼飛行器的翼型優化。

(2)本文所用的動量源方法，將旋翼槳葉對空氣的周期性擾動通過時間平均的方法轉化為“準定常”流動，該方法能在較大程度上模擬旋翼下洗流場特性。

(3)對比兩種速度設定，設定一沒有考慮旋翼的影響，設定二的邊界條件是根據旋翼后方的實際氣流速度確定的。設定二采用的邊界條件更符合實際，在0°攻角時，比設定一優化的翼型生成的機翼升阻比更大，且能在較大的攻角范圍內提高機翼升阻比。