飛機結(jié)構(gòu)有限元分析中分布載荷的離散化處理算法

尹建軍，李高勝，姚雄華

(1.航空工業(yè)第一飛機設(shè)計研究院 結(jié)構(gòu)設(shè)計所，西安 710089)(2.航空工業(yè)第一飛機設(shè)計研究院 總設(shè)計師辦公室，西安 710089)

0 引 言

在航空領(lǐng)域，有限元分析已經(jīng)成為現(xiàn)代飛機結(jié)構(gòu)設(shè)計中必不可少的重要一環(huán)。有限元方法的本質(zhì)是，把實際結(jié)構(gòu)由連續(xù)彈性體受分布體力和分布面力作用下求解位移場的無限自由度問題，轉(zhuǎn)換成離散結(jié)構(gòu)僅在結(jié)點處受結(jié)點載荷作用，求各結(jié)點位移的有限自由度問題[1-3]。因此，有限元法分析第一個步驟即為離散化，包括結(jié)構(gòu)的離散化和載荷的離散化。載荷的離散化是把單元內(nèi)部的集中力、分布力按照靜力等效的原則移置到結(jié)點上，成為等效結(jié)點載荷。

由于結(jié)構(gòu)強度、氣動彈性等設(shè)計工作中對載荷離散化的大量應(yīng)用需求，尤其在氣動彈性設(shè)計時，需要將每一次迭代結(jié)果的氣動載荷施加到結(jié)構(gòu)結(jié)點上。通常是在氣動結(jié)點上直接積分，得到氣動載荷的集中力，然后通過樣條插值得到結(jié)構(gòu)網(wǎng)格上的等效載荷值[4-5]。國內(nèi)對該方面開展的研究較多。王專利[6]通過飛機升降舵的實例證明了“多點排”氣動載荷分配算法的效率和精度；尹晶等[7]根據(jù)飛機機翼剖面氣動力載荷分布的基本規(guī)律,在已知剖面載荷總量、合力作用點位置及給定剖面弦長的條件下,提出一套轉(zhuǎn)軸橢圓和轉(zhuǎn)軸拋物線的幾何算法,利用編程計算快速給出壓力載荷分布沿弦長的幾何描述,繼而可快速地分配到翼剖面結(jié)構(gòu)結(jié)點上；高尚君等[8]采用基于彈簧-懸臂梁物理模型的最小變形能的載荷轉(zhuǎn)換方法，解決了載荷轉(zhuǎn)換前后結(jié)點重合引起的無法計算的問題；胡亮文等[9]構(gòu)造了三種不同形式的壓力場曲面函數(shù)，通過積分求得任意微元面積內(nèi)的氣動力及其作用點，按照最小變形能原理將積分得到的氣動載荷分配到有限元結(jié)點上；雷莉等[10]對傳統(tǒng)的三點排[11]、四點排[12]和多點排[11]方法進行對比，得到不同方法轉(zhuǎn)換后的結(jié)構(gòu)有限元結(jié)點載荷，三種方法都可以模擬氣動載荷，其中多點排效果最優(yōu)；張建剛等[13]根據(jù)原始氣動壓力點數(shù)值，采用樣條曲面擬合方法得到翼面壓力分布曲面及有限元結(jié)點上的壓力值，在有限元模型單元上積分得到有限元結(jié)點載荷。此外，還研發(fā)了不同的載荷轉(zhuǎn)換方法[14-15]。

三點排的效率高，但三個有限元結(jié)點需滿足如下要求：三個有限元結(jié)點與待轉(zhuǎn)換載荷結(jié)點距離最近，三個有限元結(jié)點不共線，待轉(zhuǎn)換載荷結(jié)點位于三個有限元結(jié)點所圍區(qū)域之中。為了滿足上述要求，會犧牲一定的效率。多點排方法效率偏低，當(dāng)選取的結(jié)點數(shù)量較多時，計算耗時巨大。對于三點排、四點排及多點排方法，計算過程中會用到待轉(zhuǎn)換載荷結(jié)點與有限元結(jié)點之間的間距，當(dāng)待轉(zhuǎn)換載荷結(jié)點位于結(jié)點上的時間距為零，作為分母程序報錯。為了避免錯誤，會人為引入一定誤差。

本文利用薄板彎曲單元理論，針對飛機結(jié)構(gòu)設(shè)計中需要進行離散化處理的兩種不同類型的載荷數(shù)據(jù)，提出分布載荷離散化處理的算法，并對實際應(yīng)用中舍棄結(jié)點載荷力矩分量處理方法的合理性進行說明。

1 分布載荷數(shù)據(jù)類型

1.1 氣動載荷

在飛機設(shè)計院所中，氣動載荷一般由氣動力載荷專業(yè)提供給結(jié)構(gòu)強度專業(yè)設(shè)計人員用于有限元分析，其形式為氣動力網(wǎng)點上的氣動力載荷列陣。氣動力網(wǎng)點，通常是展向等百分線與若干弦向控制線相交形成的網(wǎng)點群(氣動力)[2]。氣動分布載荷數(shù)據(jù)一般以文本文件或數(shù)據(jù)庫形式提供給結(jié)構(gòu)強度專業(yè)，該數(shù)據(jù)包含以下信息：

(1)氣動力網(wǎng)點坐標(biāo)及相應(yīng)坐標(biāo)系；

(2)載荷設(shè)計工況代號及相應(yīng)的飛機狀態(tài)參數(shù)(包括飛機重量，滾轉(zhuǎn)、俯仰、偏航角速度和角加速度，過載，速壓等)；

(3)氣動力網(wǎng)點上的氣動力載荷列陣(上、下表面的壓力系數(shù))。

在氣動力網(wǎng)格尺寸足夠小的情況下，可以認(rèn)為氣動力網(wǎng)點處的壓力均勻作用在對應(yīng)的微元上，用網(wǎng)點壓力系數(shù)乘以速壓可以獲得該氣動力網(wǎng)點處的氣動力，該力為作用在網(wǎng)點上的集中力。即氣動力載荷專業(yè)提供的數(shù)據(jù)實際已經(jīng)將連續(xù)分布的氣動力離散化為有限的集中載荷，結(jié)構(gòu)有限元載荷的離散化處理本質(zhì)上是把單元上的非結(jié)點集中載荷按靜力等效原則移置到結(jié)點上。

1.2 慣性載荷

慣性載荷是由質(zhì)量分布數(shù)據(jù)與過載相乘得到的。質(zhì)量分布數(shù)據(jù)由重量專業(yè)提供，數(shù)據(jù)形式為質(zhì)量網(wǎng)點上的質(zhì)量列陣。質(zhì)量分布通常是不規(guī)則的，考慮計算需要，重量專業(yè)按照規(guī)定的方法選定適當(dāng)數(shù)量的質(zhì)量網(wǎng)點，然后把所有結(jié)構(gòu)和非結(jié)構(gòu)質(zhì)量按質(zhì)量等效原則堆聚到質(zhì)量網(wǎng)點上，形成質(zhì)量列陣[2]。質(zhì)量分布數(shù)據(jù)包含以下信息：

(1)質(zhì)量網(wǎng)點坐標(biāo)及相應(yīng)的坐標(biāo)系；

(2)質(zhì)量網(wǎng)點上的質(zhì)量數(shù)據(jù)。

從結(jié)構(gòu)有限元分布載荷離散化處理的角度看，慣性載荷具有與氣動載荷同樣的特點，即已經(jīng)離散化為集中力點集，離散化處理的目標(biāo)是把不在結(jié)點上的載荷移置到結(jié)點上。

1.3 壓差載荷

座艙、客艙等有乘員的艙室，燃油箱內(nèi)部等空間一般需要增壓，壁板和框、梁腹板要承受分布的內(nèi)外壓差載荷。壓差載荷的特點是沿結(jié)構(gòu)表面的法向作用，均勻分布。這是一種簡單的分布面力，壓差集度為常數(shù)。

1.4 液體壓力載荷

水上飛機的水下部分、燃油箱、汲水容器等結(jié)構(gòu)會受到液體壓力作用。液體壓力隨深度按線性規(guī)律分布，即p=ρgh。

綜上所述，飛機結(jié)構(gòu)有限元分析需對兩類載荷進行離散化處理：其一為上游專業(yè)提供的網(wǎng)點載荷列陣數(shù)據(jù)；其二為以均布或線性分布等簡單形式作用的面載荷。

2 單元類型與特點

2.1 單元形狀

飛機結(jié)構(gòu)一般為薄壁結(jié)構(gòu)，外形曲面由多個平面近似，通常按由桁條與肋、框劃分成的實際格子來劃分單元，這樣可以更加真實地模擬各結(jié)構(gòu)元件的承載功能，且更易于結(jié)果分析。利用矩形、任意四邊形和三角形單元組成的網(wǎng)格可以近似任何薄壁結(jié)構(gòu)。

2.2 單元承載特點

當(dāng)薄板承受一般載荷時，總可以把每一個載荷分解為兩個分載荷，一個是作用在薄板中面之內(nèi)的縱向載荷，另一個是垂直于中面的橫向載荷。對于縱向載荷，可以認(rèn)為它們沿薄板厚度均勻分布，因而它們所引起的應(yīng)力、形變和位移，可以按平面應(yīng)力問題進行計算。橫向載荷將使薄板彎曲，它們所引起的應(yīng)力、形變和位移，可以按薄板彎曲問題進行計算[1]。

在飛機結(jié)構(gòu)設(shè)計中，大量應(yīng)用薄壁構(gòu)件，例如壁板蒙皮及框、梁、肋的腹板等，它們在結(jié)構(gòu)有限元模型中簡化為平板單元，按承載特點分為兩種單元：一是平面應(yīng)力單元，另一種是薄板單元。

平面應(yīng)力單元基于彈性力學(xué)平面問題理論，每個結(jié)點的位移、應(yīng)變、應(yīng)力、結(jié)點力都是在平面內(nèi)的，單元與單元之間結(jié)點是鉸接的，結(jié)點載荷只有力分量沒有力矩分量。平面應(yīng)力單元不能承受面外載荷。在飛機結(jié)構(gòu)有限元模型中，采用平面應(yīng)力單元的區(qū)域，面外力由單元周邊布置的桿、梁等單元承受。

薄板單元基于彈性力學(xué)薄板彎曲理論，相鄰單元之間有法向力和力矩的傳送，因此必須把結(jié)點當(dāng)成剛性連接的。每個結(jié)點具有3個參數(shù)(3個自由度)：1個線位移(撓度w)和2個角位移(繞x軸的轉(zhuǎn)角θx，繞y軸的轉(zhuǎn)角θy)。即

(1)

對應(yīng)的結(jié)點力為

(2)

3 等效結(jié)點載荷

3.1 基本原理

在有限元分析中，認(rèn)為單元與單元之間僅通過結(jié)點相互聯(lián)系。因此，在結(jié)構(gòu)離散化過程中，如果外載荷不是直接作用在結(jié)點上，那么就需要將非結(jié)點載荷向結(jié)點等效移置。即把作用在結(jié)構(gòu)上的真實外載荷理想化為作用在結(jié)點上的集中載荷。

整個結(jié)構(gòu)的非結(jié)點載荷的移置按單元進行，即將各單元所受的非結(jié)點外載荷分別移置到各單元相應(yīng)的結(jié)點上；然后，在公共結(jié)點處應(yīng)用力的疊加原理，便可求出整個結(jié)構(gòu)的結(jié)點載荷列陣。因此只需解決單元載荷移置問題就解決了整個結(jié)構(gòu)的載荷移置。

單元載荷移置所遵循的原則是能量等效原則，即單元的實際載荷與移置后的結(jié)點載荷在相應(yīng)的虛位移上所做的功相等。

對集中力有

Re=NTP

(3)

對面力有

Re=?ΩeNTqdxdy

(4)

3.2 網(wǎng)點載荷列陣移置

網(wǎng)點載荷列陣按集中力處理，將單元內(nèi)部的載荷點逐一按照公式(3)移置到單元的結(jié)點上，再將其全部疊加就獲得了等效結(jié)點載荷。

矩形薄板單元如圖1所示，將位移模式代入式(3)并計算整理后，有

(5)

(6)

圖1 矩形薄板單元Fig.1 Rectangular thin plate element

對任意四邊形薄板單元，通過坐標(biāo)變換，將整體坐標(biāo)系下的任意四邊形映射到局部坐標(biāo)系的單位正方形單元，如圖2所示。

(a)映射前單元

(b)映射后單元圖2 任意四邊形映射為單元正方形Fig.2 An arbitrary quadrilateral mapped to a unit square

當(dāng)假定結(jié)點載荷的力矩分量為零時，等效結(jié)點載荷為

(7)

(8)

(9)

式中：Ni為形函數(shù)；|J|為整體坐標(biāo)(x，y)與局部坐標(biāo)(ξ，η)的雅可比行列式。

三角形薄板單元如圖3所示，采用面積坐標(biāo)按式(10)獲得形函數(shù)，代入式(3)即可得到載荷移置的解。

N=[NiNjNm]

=[NiNxiNyiNjNxjNyjNmNxmNym]

(10)

(11)

圖3 三角形薄板單元Fig.3 Triangular thin plate element

3.3 簡單分布面力的移置

對矩形薄板單元(圖1)，當(dāng)單元上受均勻分布載荷時，設(shè)載荷集度為常量q0，由式(4)計算整理可得

(12)

如果單元承受在x方向線性變化的法向載荷，則需要對分布函數(shù)積分。

任意四邊形單元和三角形單元受簡單分布載荷的處理方法與矩形單元類似。

3.4 力矩分量的處理

移置到各結(jié)點的載荷中，力矩載荷隨著單元尺寸的減小而減小，在較小的單元中，它們對位移及內(nèi)力的影響遠小于法向載荷的影響，因此，在實際計算時，可以將力矩載荷略去不計[3]。但是，在飛機結(jié)構(gòu)有限元模型中，單元按結(jié)構(gòu)實際格子劃分時，尺寸并不小，按上述處理方式獲得的結(jié)點載荷力矩分量也很大。如果觀察該結(jié)點相鄰單元的結(jié)點載荷力矩分量，可以看出它們是相互抵消的。因此，在承受分布力的結(jié)構(gòu)內(nèi)部，有限元結(jié)點的力矩載荷仍可忽略不計，但是在邊界區(qū)域，例如增壓艙與非增壓艙界面處，則不能忽略。

4 算例分析

4.1 簡單算例

取長度1 000(x方向)，寬度100(y方向)平面板，受均勻分布的面外載荷。分布載荷作用點為2×2網(wǎng)格結(jié)點，單個結(jié)點上的載荷為1。

結(jié)構(gòu)網(wǎng)格大小10×10，轉(zhuǎn)換前后載荷云圖如圖4所示。

(a)轉(zhuǎn)換前載荷分布

(b)轉(zhuǎn)換后載荷分布圖4 均布載荷轉(zhuǎn)換前后對比Fig.4 Contrast before and after uniform load conversion

從圖4可以看出：轉(zhuǎn)換后載荷分布與轉(zhuǎn)換前相一致，量值為轉(zhuǎn)換前結(jié)點載荷的25倍，轉(zhuǎn)換后載荷在邊緣結(jié)點上的值偏小。

考慮三類結(jié)構(gòu)網(wǎng)格單元：A類單元為內(nèi)部網(wǎng)格單元，B類單元為邊緣網(wǎng)格單元，C類單元為角部網(wǎng)格單元。與每個結(jié)構(gòu)網(wǎng)格單元相關(guān)的氣動結(jié)點單元關(guān)系如圖5所示。

圖5 典型有限元單元內(nèi)部載荷點分布Fig.5 Load point distribution in typical finite element

對于A類單元，落在單元內(nèi)部的氣動結(jié)點(圖中米字結(jié)點)，其全部載荷均作用在單元內(nèi)；對于邊緣氣動結(jié)點(圖中圓圈結(jié)點)，其載荷值的一半作用在單元內(nèi)；對于角部氣動結(jié)點(圖中方實心結(jié)點)，其載荷值的四分之一作用在單元內(nèi)。當(dāng)氣動結(jié)點上為均布載荷時(假設(shè)為1)，單元上的載荷總和為25。每個結(jié)點由4個單元公用，每個單元包含4個單元，轉(zhuǎn)換到每個結(jié)點上的載荷理論為25。

對于B類單元，單元某一邊緣上的氣動結(jié)點全部作用在單元內(nèi)，單元上的載荷總和為27.5。邊緣上的兩個結(jié)點只有兩個單元的載荷對其有影響，已知內(nèi)部兩個結(jié)點載荷為25，邊緣結(jié)點載荷為15。

對于C類單元，單元兩個邊緣上的氣動結(jié)點全部作用在單元內(nèi)，單元上的載荷總和為30.25，已知內(nèi)部結(jié)點和邊緣結(jié)點載荷分別為25和15，角結(jié)點上的載荷為9。

轉(zhuǎn)換后載荷大小與理論值相一致。

采用同樣的方法，分析沿x方向線性分布的面外載荷，載荷大小為F=0.01x。

得到轉(zhuǎn)換前后的載荷分布如圖6所示，可以看出：載荷分布與轉(zhuǎn)換前相一致。

(a)轉(zhuǎn)換前載荷分布

(b)轉(zhuǎn)換后載荷分布圖6 線性分布載荷轉(zhuǎn)換前后對比Fig.6 Contrast before and after linear distribution load conversion

4.2 工程算例

取某大展弦比機翼翼載進行轉(zhuǎn)換分析。輸入數(shù)據(jù)為氣動專業(yè)提供的翼面上壓力系數(shù)分布及對應(yīng)速壓，通過轉(zhuǎn)換得到結(jié)構(gòu)有限元網(wǎng)格上的結(jié)點載荷。

4.2.1 總載分析

對轉(zhuǎn)換前后的數(shù)據(jù)進行總力和總矩(相對飛機對稱面的彎矩)比較，結(jié)果及誤差分析如表1所示，可以看出：從飛機總體受載角度分析，與氣動力載荷相比，轉(zhuǎn)換后的載荷誤差較小，均在3%以內(nèi)。

表1 載荷轉(zhuǎn)換前后的總載對比Table 1 Total load comparison before and after load conversion

4.2.2 展向分布剪力、彎矩分析

對轉(zhuǎn)換后的結(jié)點載荷沿展向積分，分別得到翼載的剪力、彎矩沿展向的分布，如圖7所示。

(a)上翼面剪力沿展向的分布

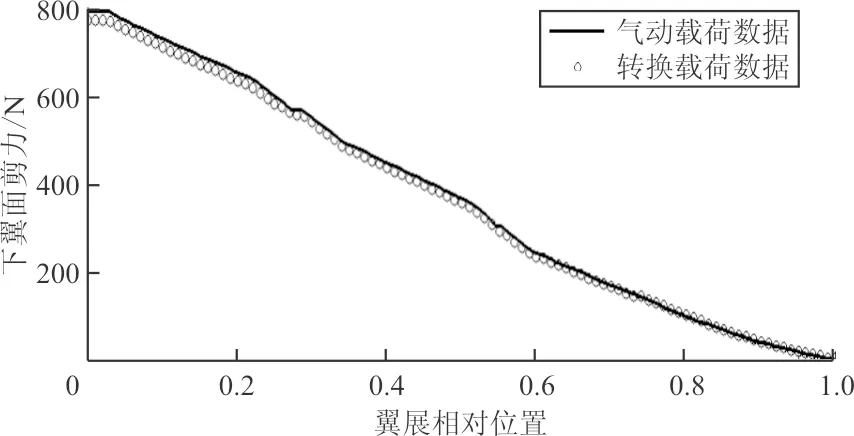
(b)下翼面剪力沿展向的分布

(c)上翼面彎矩沿展向的分布

(d)下翼面彎矩沿展向的分布圖7 轉(zhuǎn)換前后展向截面剪力及彎矩對比圖Fig.7 Contrast diagram of shear force and bending moment of spread section before and after conversion

從圖7可以看出：分布載荷數(shù)據(jù)與氣動數(shù)據(jù)吻合較好，由于誤差累積，在翼尖處(橫軸最大)誤差最小，翼根處(橫軸為零)誤差最大，翼根處的剪力、力矩與翼面上總力和總矩相等，該處載荷誤差如表1所示。

4.3 算例分析總結(jié)

通過簡單算例及工程算例的載荷分析，轉(zhuǎn)換后的結(jié)點載荷與氣動載荷對比誤差較小。通過本文所提出的方法得到的離散化載荷，能夠真實地反映實際載荷分布，且程序?qū)崿F(xiàn)簡單，效率較高，無人為誤差的引入，可用于工程計算。

5 誤差分析

氣動載荷是連續(xù)變化分布的，上述方法將其處理為微元上的均布載荷，在相鄰微元邊界處是不連續(xù)的，這將產(chǎn)生計算誤差，文獻[9]和文獻[13]提出的方法其目的就是消除該誤差。實踐證明，在飛機設(shè)計的大多數(shù)情況，采用本文的算法進行分布載荷的離散化，其誤差在可接受范圍內(nèi)。

6 結(jié) 論

(1)氣動力、慣性力等以網(wǎng)點列陣形式提供的載荷數(shù)據(jù)，根據(jù)薄板單元集中力移置公式按單元移置到結(jié)點上；均布和線性分布的載荷，根據(jù)薄板單元面力移置公式按單元移置到結(jié)點上。

(2)在分布載荷作用區(qū)域內(nèi)部的單元，結(jié)點載荷的力矩分量總和為零，可以忽略不計，但在分布載荷作用區(qū)域的邊界處則不能忽略。

(3)本文所提方法實現(xiàn)的載荷轉(zhuǎn)換，程序?qū)崿F(xiàn)簡單，效率較高，無人為誤差的引入。系統(tǒng)誤差在可接受范圍內(nèi)。