與階乘有關的兩個方程的解

姜蓮霞，張四保

(喀什大學 數學與統計學院，新疆 喀什 844008)

在數論中，有關方程解的研究有著廣博的研究成果，如文獻[1-2]就討論了2個方程解的問題。設n!是正整數n的階乘,對于有關階乘的方程解問題的研究是方程研究中最基礎、最重要的問題之一[3]。對于有關階乘的方程解問題，Bencze 和Simmons等提出了一系列的問題與猜想，如文獻[4-7]。在國內，對于有關階乘的方程解問題的討論也有著豐富的研究內容，如文獻[8-11]。本文在樂茂華教授對有關階乘的方程解問題討論的基礎上，討論了兩個形式更為一般的方程解問題。

1 定理1及其證明

定理1 除p=2之外，方程

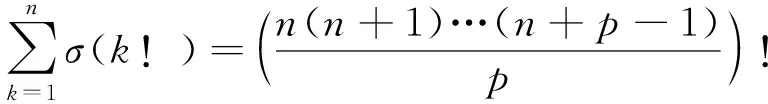
(1)

無解，其中p是滿足p≥2的整數。

證明 當p=2時，此時方程就是文獻[12]所討論的方程。以下討論p為p≥3的整數的情況。

當n=1時，有σ(1！)=1，而

(1×2×…×(p-1))!≥2

因而n=1不是方程(1)的解。

當n=2時，有

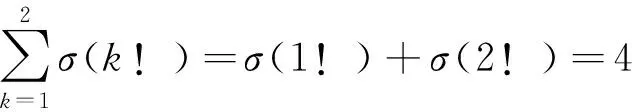
而

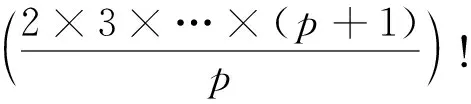
(2×3×…×(p-1)×(p+1))!≥8!

因而n=2不是方程(1)的解。

當n=3時，有

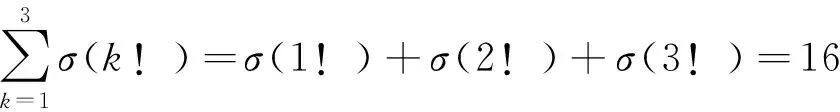
而

(3×4×…×(p-1)×(p+1)×(p+2))!≥20!

因而n=3不是方程(1)的解。

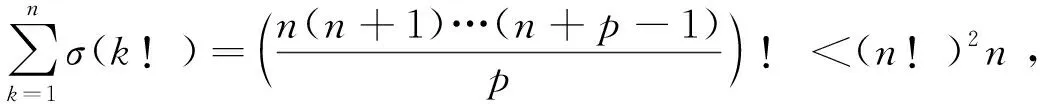
(n!)n<(n+1)!

(2)

當n≥4時，(2)式左端是

定理1證畢。

2 定理2及其證明

定理2 除p=2之外，方程

(3)

無解，其中p是滿足p≥2的整數。

證明 當p=2時，此時方程就是文獻[14]所討論的方程。以下討論p為p≥3的整數的情況。

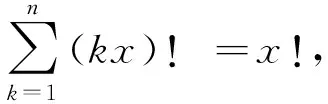
(1×2×…×(p-1)x)!≥(2x)!

因而n=1不是方程(3)的解。

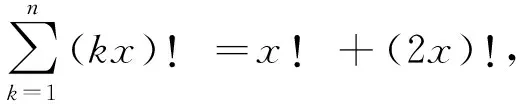
(2×…×(p-1)×(p+1)x)!≥(8x)!

若n=2是方程(3)的解，則有x!+(2x)!=(8x)!,有(8x)!-x！-(2x)!=0,從而有(x+1)(x+2)…(8x)-1-(x+1)(x+2)…(2x)=0，

因而有

(x+1)(x+2)…(2x)[(2x+1)(2x+2)…

(8x)-1]=1

(4)

顯然(4)式是無正整數解，因而n=2不是方程(3)的解。

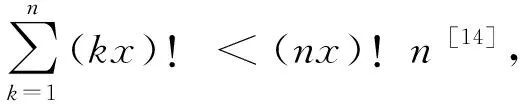
(5)

顯然,當n≥3時(5)式不成立，所以當n≥3時，方程(3)亦無解。

定理2證畢。