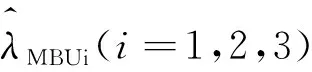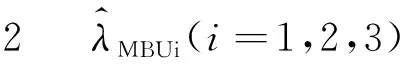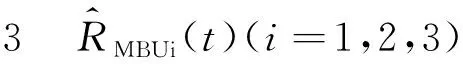指數分布無失效數據下參數的單側M-Bayes估計
李億民
(山東理工大學 數學與統計學院,山東 淄博 255049)
對于指數分布的定數截尾壽命試驗,已經有了比較成熟的處理方法[1-2]。對于定時截尾壽命試驗,如果規定的截尾時間較短,特別是對于高可靠產品,在規定時間內失效個數往往比較少,甚至出現無失效的情形[3-5]。
設產品壽命T服從參數為λ的指數分布,即
T~f(t)=λexp{-λt},t>0
(1)
式中:λ>0為產品的失效率,R(t)=exp{-λt}為產品在時刻t的可靠度。
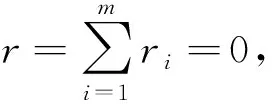
為了充分利用產品的試驗信息{(ni,0,τi),i=1,2,…,m}和總體參數的先驗信息,對式(1),本文試圖給出參數λ的單側M-Bayes置信上限[6]和可靠度R(t)的單側M-Bayes置信下限,并討論估計量的有關性質。
1 失效率λ的單側M-Bayes置信上限定義


對于參數λ,可以選擇其先驗密度函數為
π(λ|a)=aexp(-aλ),λ>0
(2)
式中a>0為超參數[6]。
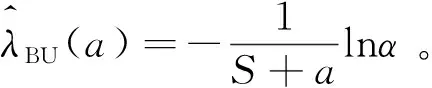
證明 在無失效數據{(ni,0,τi),i=1,2,…,m}情況下,樣本的似然函數為L(0|λ)=exp{-Sλ},若λ的先驗密度函數由式(2)給出,由Bayes定理,得參數λ的后驗密度函數為
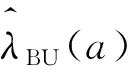
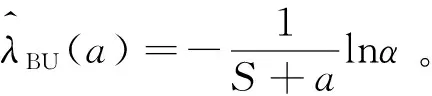
對于a>0,假定其上界為c,由于不知a服從(0,c)上的具體分布類型,為此,假定其密度函數為
(3)
(4)
式中j≥0。當j=0時,即為(0,c)上的均勻分布;兩種密度函數從圖形上差別較大,式(3)為a的嚴格遞減函數,式(4)為a的嚴格遞增函數。在對參數沒有任何信息時,常常選用無信息先驗分布,即選擇均勻分布。在式(3)、式(4)中,選擇了參數的單調遞減函數和單調遞增函數,即選擇了比較極端的先驗分布情況下對參數進行估計,目的在于比較極端情況下參數估計結果的差異,從而說明該方法的穩健性。
2 失效率λ的單側M-Bayes置信上限函數性質

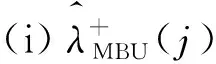
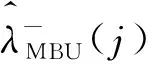

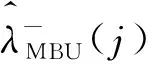
證明 (i)由定義,得
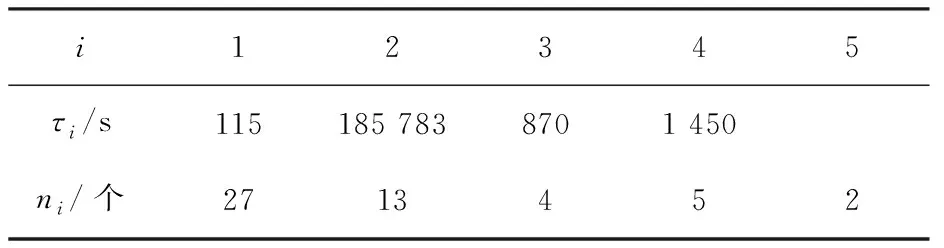
對任意0 (5) 所以 為便于應用,本文給出a的3個特殊先驗密度函數為: (6) (7) (8) (i)固定c,參數λ的置信水平為1-α(0<α<1)的單側M-Bayes置信上限分別為: 現有某型號發動機的一組無失效數據,見表1。根據工程經驗,該產品的壽命T服從失效率為λ的指數分布式(1)。 表1 發動機的無失效數據 i 123 4 5τi/s115185 783 8701 450ni/個27 13 4 52 c 15001 0003 0005 000極差λ^MBU11.885 0×10-41.870 4×10-41.856 1×10-41.802 2×10-41.753 0×10-42.320×10-5λ^MBU21.884 9×10-41.856 0 ×10-4 1.828 1×10-4 1.726 8×10-41.639 0×10-42.459×10-5λ^MBU31.884 9×10-41.846 4×10-41.809 5×10-4 1.677 0×10-41.563 2×10-43.217×10-5極差0.01×10-62.40×10-6 4.66×10-612.52×10-618.98×10-6 c 1 5001 000 3 0005 000極差R^MBU1(100)R^MBU2(100)R^MBU3(100)極差0.9813 2 0.981 47 0.981 610.982 140.982 620.001 290.981 330.981 610.981 890.982 880.983 740.002 410.981 330.981 710.982 070.983 370.984 490.003 160.000 010.000 240.000 460.001 230.001 87R^MBU1(500)R^MBU2(500)R^MBU3(500)極差 0.910 050.910 720.911 370.913 830.916 080.006 02 0.910 060.911 380.912 650.917 280.921 320.011 260.910 060.911 810.913 500.919 670.924 820.014 76 0.000 010.001 090.002 130.006 840.008 74 從計算結果看,無論是失效率λ的還是可靠度R(t)的單側M-Bayes估計,在0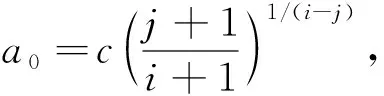
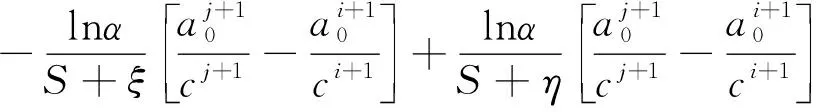
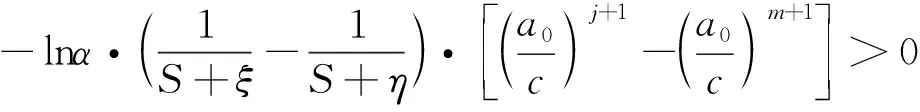
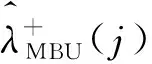
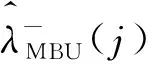
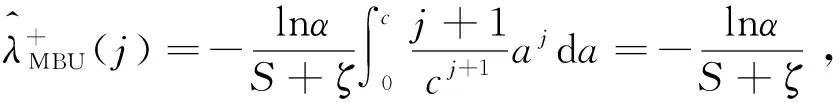
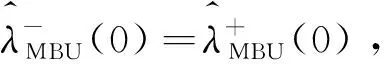
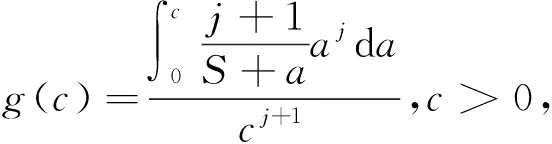
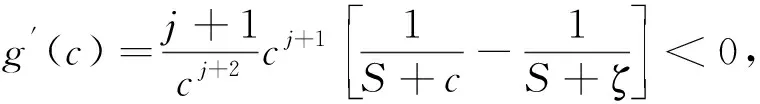
3 可靠度R(t)的單側M-Bayes置信下限定義
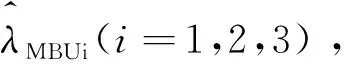

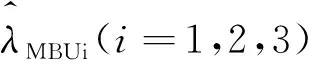
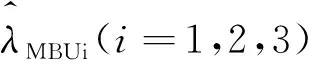
4 實例分析
Tab.1 No failure data for engine