自適應的高精度中心-WENO混合格式

田 奇郭 元梁 賢李新亮

(1.北方民族大學 數學與信息科學學院,銀川 750021；2.中國科學院大學 工程科學學院,北京 100049；3.中國科學院力學研究所 高溫氣體動力學國家重點實驗室,北京 100190)

0 引 言

在數值模擬復雜流體流動問題中,特別是在研究非定常多尺度流動的細微結構及其機理時,高精度格式比低精度格式更能準確地捕捉各種小尺度量,特別像湍流、旋渦、氣動聲學等流動問題。因而,近年來高精度低耗散數值方法的研究越來越受到重視。對于可壓縮復雜流動的精細模擬,除了需要高精度、低耗散地分辨小尺度流動細節,還需要對激波進行捕捉,并盡量避免數值振蕩。1994年,Liu等對ENO格式進行了改進[1],提出了 WENO(Weighted Essential Non-Oscillatory)格式,WENO格式成為目前應用最廣泛的激波捕捉格式。隨即,Jiang和Shu對該方法進一步改進[2],提出了新的光滑度量因子,使得 WENO格式的精度進一步得到提高。數值試驗表明,Jiang和Shu的WENO格式具有較強的魯棒性,因而被廣泛地使用。此后,人們對WENO格式進行著一系列測試、評估和改進[3-7]。在國內,高精度激波捕捉格式的構造也得到了廣泛的重視。鄧小剛等[8-9]構造了高精度加權緊致格式WCNS和高精度耗散加權緊致格式DWCNS。張涵信等[10]基于三階ENN格式,引入加權函數,構造了一種具有四階或五階精度的WENN高階格式。傅德薰、馬延文先后提出了耗散比擬法[11]和群速度控制方法[12],以及三階和五階精度的迎風緊致格式以及超緊致格式[13]。任玉新等[14]提出了色散最優耗散可調的高分辨率線性格式。李新亮、何志偉等[15-16]提出非線性譜分析優化的保單調格式和群速度控制方法。

一般而言,低耗散特性及強激波捕捉能力不容易兼顧。因而近年來發展出了混合格式(Hybrid schemes),即將兩種格式混合使用,在間斷或大梯度區采用強魯棒的激波捕捉格式,而在相對光滑區采取無耗散的中心格式或低耗散的線性格式。Pirozzoli[17]運用光滑識別器作為判據,在光滑區使用緊致格式而在非光滑區使用WENO格式,從而較好實現了分辨小尺度波與捕捉激波的效果。Ren等使用了加權思想[5],將WENO格式與緊致格式混合使用,避免了兩種格式之間的“硬切換”,從而起到了更好的效果。

本文的主要工作就是基于WENO格式中的光滑因子,構建一種新型的加權函數,并在此基礎上將經典的7階WENO格式和8階中心格式組合成混合格式,實現數值耗散的自適應控制,構造出一種自適應低耗散的數值格式。通過對格式進行非線性色散、耗散特性分析,對比研究格式在不同波數下的色散和耗散特性,并經若干一維和二維算例數值驗證新格式對流場間斷及小尺度波的捕捉能力,以期為可壓縮湍流的數值模擬提供一種新的方法。

1 數值方法

1.1 數值格式構造方法

使用Jiang等提出的WENO7格式[2]為通量插值形式,本文使用原始變量重構形式。WENO7格式[18]為:

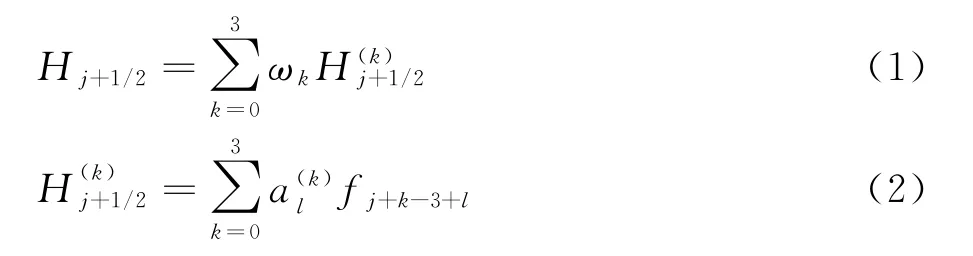
其中:為模板各給出的通量,ωk為各個模板對應的非線性權值,相應的表達式為:

根據Taylor級數展開式容易給出光滑區域的理想加權因子:

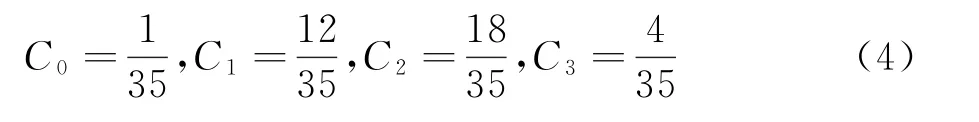
光滑度量因子βk的表達式為:

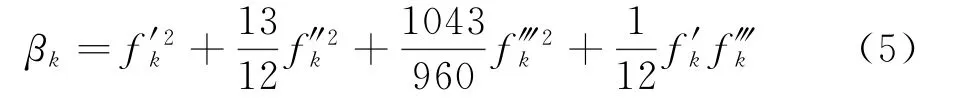
八階中心格式的數值通量表達式為:

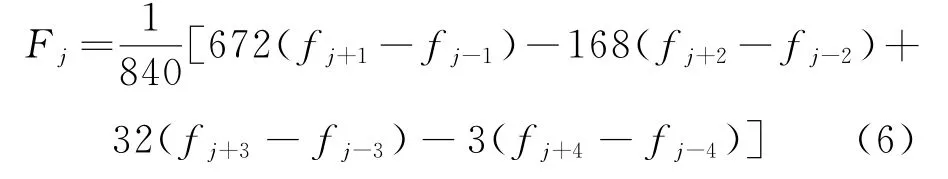
半點格式的表達式為:

由于WENO格式的耗散相對較大,而中心格式無耗散,因此本文的目的是將兩種格式進行混合,從而構造出一種低耗散的數值格式。基于這一思想,在此引入加權函數σ,格式變為:

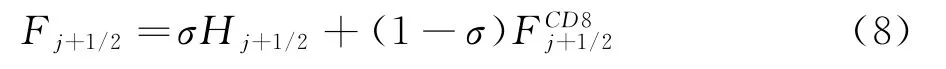
為實現對該混合格式數值耗散的自適應控制,本文建立起加權因子σ與光滑度量因子βk的關系。根據βk在光滑區時很小,而在間斷區相對較大這一特點,本文在此構造σ與βk的關系式為:

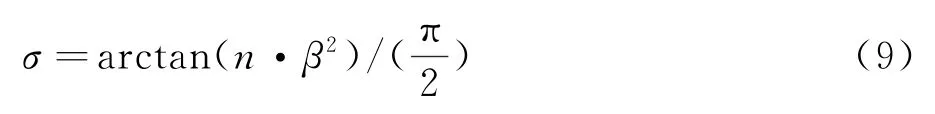
在流場光滑區域βk很小,當βk趨于0時,σ也趨于0,此時格式為近似八階中心格式,將具有很低的耗散；在流場非光滑區域βk值相對較大,此時σ趨于1,因此格式將會保留足夠的耗散來抑制非物理振蕩。這樣,該格式將會具有中心格式與WENO格式共同的特點。

1.2 數值格式誤差分析

采用Fourier精度分析法[19]分析該空間離散格式,所得到的修正波數的虛部Ki和實部Kr分別表示數值格式的色散和耗散效應,α為波數。從圖1中可以看出,本文H-WENO7-CD8格式的色散誤差要比經典的WENO7更小,而WENO格式在高波數區存在較大的耗散誤差,其耗散也在高波數區也比WENO7要小,原因是H-WENO7-CD8格式是通過經典的WENO7格式與中心格式加權組合而成,而中心格式無耗散。這就在一定程度上降低了新格式的耗散。

2 數值算例

2.1 激波-密度波干擾問題

該問題為一個馬赫數為3的運動激波和正弦密度波相互干擾,使用各空間離散格式模擬一維激波-密度脈動干涉算例[20],以測試數值方法對小尺度結構的分辨能力。該控制方程為一維的Euler方程組,初始條件為:

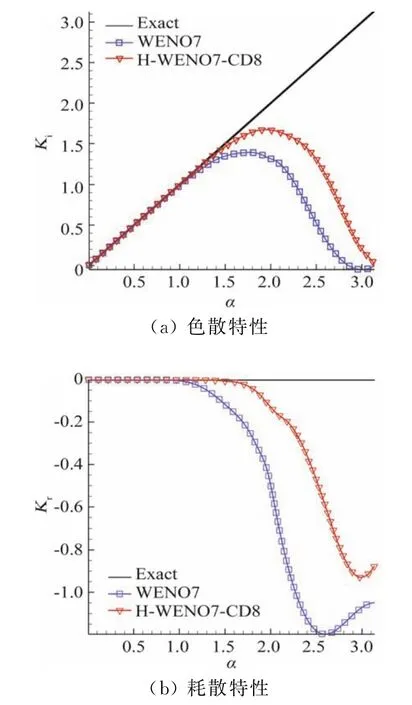
圖1 兩種不同格式的色散(a)和耗散(b)特性Fig.1 Spectral properties of two different schemes

以x＝1處為左右側分界點,最終結果在區間x＝[0,10]上進行計算,結束時間為t＝1.8。網格點數為N,由于該問題不存在解析解,因此選用N＝4001時的結果作為參考的精確解(Exact),采用Runge-Kutta方法進行時間推進,通量分裂使用Steger-Warming分裂,使用局部特征分解。

圖2給出了WENO7格式和H-WENO7-CD8格式的計算結果。可以看出,WENO格式和新格式均能較好地捕捉x＝7.4處的間斷以及x＝5.5左側的密度波動,但在該網格數下 WENO7得到的幅值明顯偏小；而H-WENO7-CD8格式不但能得到與精確解符合更好的波形,而且幅值也更接近精確解,因此新格式比WENO7對流場間斷及脈動具有更強的分辨率。

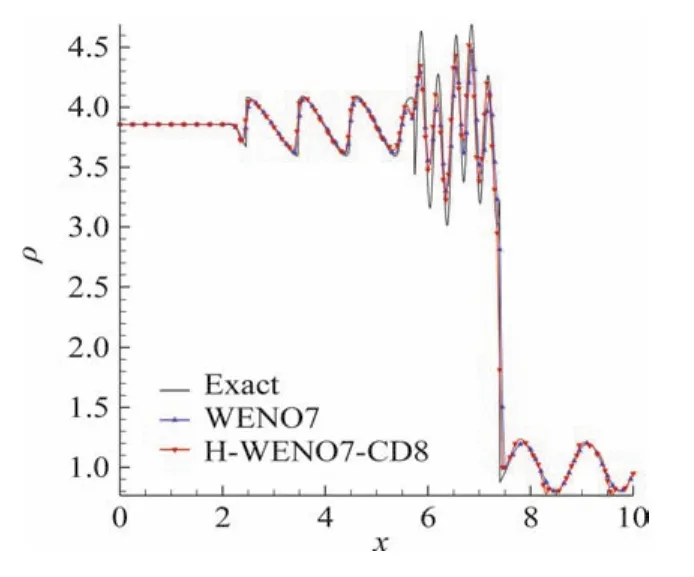
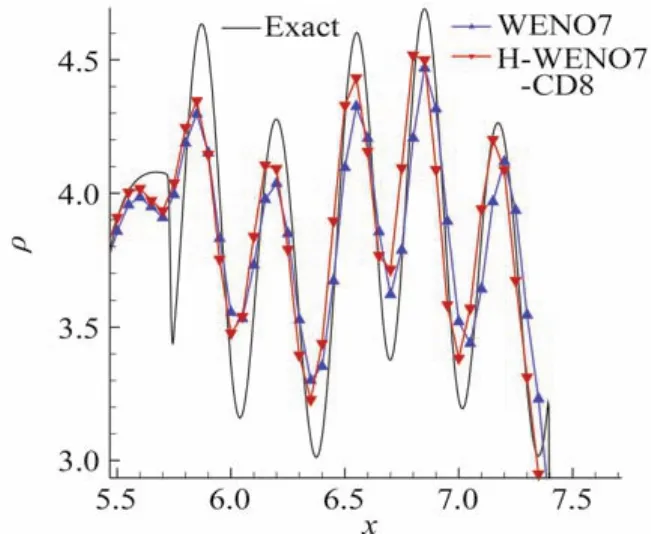
圖2 Shu-Osher問題,t＝1.8時刻的密度分布,N＝201Fig.2 Density distribution of the 1D shock/turbulence interaction at t＝1.8,N＝201

2.2 瑞利-泰勒不穩定問題

Rayleigh-Taylor(RT)不穩定性問題[19]是當兩種密度不同的流體界面有微小的擾動,且由于某種原因從重流體到輕流體的方向產生加速度時,在這兩種流體的界面上就會出現不穩定性。RT不穩定性包含很多細致結構,以此用來測試數值格式分辨率。其計算條件設置如下[19]:計算域為 [0,0.25]×[0,1]；初始時刻,輕重流體的交界面位于y＝0.5處,密度ρ＝2的流體位于界面之下,密度ρ＝1的流體位于界面之上。初始場為:

源項的表達式為S＝(0,ρ,0,ρv)T。計算最終時間t＝1.95。

圖3分別給出了WENO7和H-WENO7-CD8兩種不同格式在網格60×240和240×960上計算得到的數值結果。從圖3中可以看出,在網格60×240上不同的格式捕捉到的流動結構和相關文獻基本保持一致,密度大的流體沿中軸線流入密度小的流體,中軸線兩側形成了若干小尺度的渦結構,兩種格式均能保證質量守恒,而新格式在此粗網格上能分辨出更多的小尺度結構。網格加密到240×960之后,新格式捕捉到的小尺度渦結構仍然要比WENO7要多,這就表明了在復雜結構的數值計算中,H-WENO7-CD8格式擁有更高的數值結構分辨率。

圖3 RT不穩定性密度分布Fig.3 Rayleigh-Taylor instability：density profile

這是一個入射角為60°的馬赫數為10的激波的雙馬赫反射問題[21]。具體求解設置為:計算區域[0,0]×[4,1],下邊界y＝0,平板前緣位于x＝0.1667處,一直延伸到x＝4前,從x＝0到x＝0.1667給定波后條件；平板處采用波后壁面條件；上邊界各點的值由馬赫數為10的激波的精確運動來確定。計算最終時間為t＝0.2。

由于中心格式無耗散,而在雙馬赫反射的計算中需要數值格式有足夠的耗散,因此需要設定一個開關函數,在間斷區時,要給予WENO格式足夠的權重,在此961×241的密網格的計算中,限制式(9)中的σ≥0.94,這樣就可以有效的防止發散。

圖4給出了在網格數相同情況下,采用不同格式所計算得到的密度等值線及其在接觸間斷和馬赫桿附近的放大圖(a:WENO7；b:H-WENO7-CD8),可以看出,兩種格式均能很好的捕捉到該問題基本的流動特征,如馬赫桿、激波和滑移線。另外通過比較兩幅局部放大圖可以清楚地看到,H-WENO7-CD8格式能分辨出更多的近壁面結構,更清晰的捕捉到了滑移線的卷曲現象和小尺度的渦,表明新格式對于小尺度結構具有良好的分辨能力,具有較高的分辨率。

2.3 雙馬赫反射問題

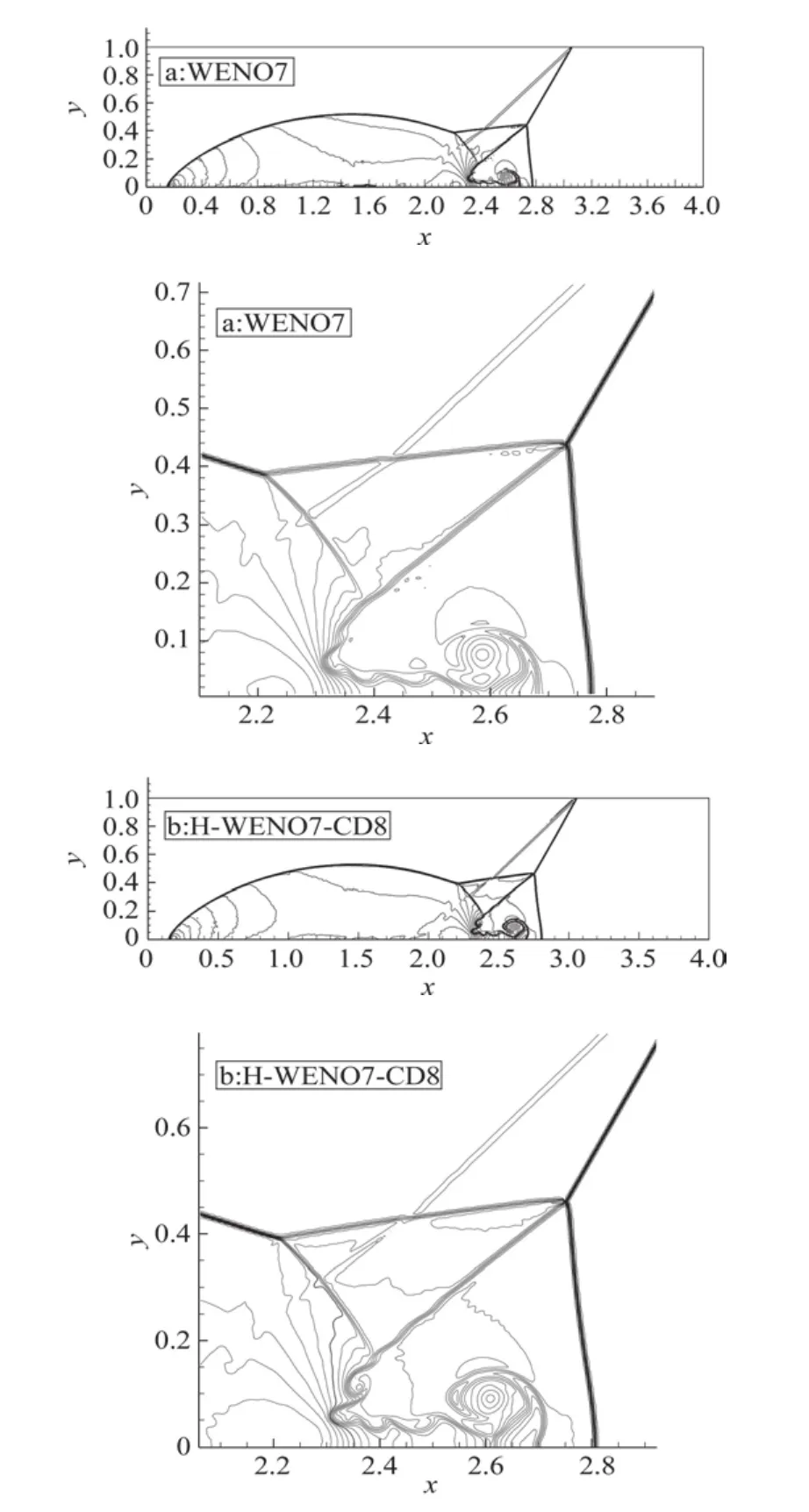
圖4 密度分布,網格點數961×241,30條等值線,從ρ＝1.731到ρ＝20.92Fig.4 Density contours of the Double Mach Reflection problem,961×241 grid

3 結 論

本文通過新型加權函數將經典的WENO格式和中心格式結合起來,利用光滑度量因子設定中心格式和WENO格式上的混合權重,實現了對格式數值耗散的自適應控制,構造出一種自適應低耗散的數值格式。通過對一維激波密度脈動干涉問題和二維的瑞利-泰勒不穩定性問題和雙馬赫問題進行數值模擬,結果表明新的格式在繼承了原WENO格式良好的激波捕捉特性的同時,具有更低的耗散,對小尺度結構更高的分辨率,并且有較好的穩定性,這也為可壓縮湍流的高分辨率數值模擬提供了一種新的備選方法。此外,本文構造格式是在均勻網格上推導的,這也是目前大多數高精度差分格式的做法。在實際應用中,對于曲面非光滑網格,格式會產生幾何誘導誤差,幾何守恒問題對計算格式的精度和穩定性都有較大的影響,將在今后的工作中考慮格式的幾何守恒律問題。

致謝：本項目得到國家自然科學基金(Nos.11472010,91441103,11372330,11472278)、國家重點研發計劃(2016YFA0401200)、科學挑戰專題項目(JCKY2016212A501)以及民用飛機專項科研(MJ-2015-F-028)的資助。感謝中國科學院力學研究所的傅德薰、馬延文研究員對本研究的幫助。感謝國家超級計算天津中心以及國家超級計算廣州中心提供計算機時。