超聲速民機聲爆理論、預測和最小化方法概述

蘭世隆

(北京航空航天大學 流體力學教育部重點實驗室,北京 100083)

0 引 言

從20世紀50年代開始,隨著超聲速軍機的發(fā)展,英、法、美、前蘇聯等國逐漸對超聲速民機產生濃厚興趣。協和號、圖144、B2707的研制大大促進了聲爆相關理論和方法的發(fā)展,這期間聲爆理論、預測方法以及聲爆最小化方法就已經基本建立起來。然而,協和號聲爆初始過壓達到2 psf,響度約為107 PLdB[1],只能在大洋上空做超聲速飛行。超聲速民機研制一度陷入低谷。隨后80年代美國重啟超聲速民機技術研發(fā)項目(HSCT),主要參與者是波音和麥道,該項目推進了聲爆理論、抑制技術和聲爆主觀接受度等方面的發(fā)展,但是當時的技術成熟度和經費還無法支持研制中型(100～200座)超聲速民機,低聲爆超聲速公務機相對容易實現[2]。協和號的退役并沒有打消人們超聲速飛行的夢想。NASA在NextGen計劃中提出了3代超聲速民機的技術要求,即N＋1超聲速公務機(2015)、N＋2小型超聲速民機(2020)、N＋3中型超聲速民機(2030),并于2009年委托波音和洛克希德馬丁公司分別進行概念設計研究和關鍵技術開發(fā)[1]。此外,2000年以來還有多個項目開展了地面風洞試驗和飛行測試,比如,F-5E聲爆形狀設定的驗證(Shaped Sonic Boom Demonstration,SSBD)[3,4],F-15B靜音錐(Quite Spike)項目[5],這些工作驗證了聲爆理論、預測方法和最小化方法(sonic boom minimization)的有效性。

近些年來,眾多飛機制造公司都在積極地開展各自的超聲速民機,特別是超聲速公務機的概念研究[6]。最近,洛克希德馬丁公司正在開展X-59 QueSST項目[7],除了要驗證低聲爆技術,還將建立聲爆及居民對聲爆的反應數據,為民機在陸地上空超聲速飛行提供立法依據。在概念設計以及遠景規(guī)劃中,廣為人知的聲爆標準是NASA在3代超聲速民機中提出的70PLdB標準,已有的工作表明,超聲速民機設計要達到此聲爆標準,難度仍然很大。困難來自于低聲爆構型設計中一些相互矛盾、相互制約的因素,比如,機體容積和細長體外形、低速起降和高速巡航的氣動性能、低阻構型與低聲爆構型等等。這些問題是超聲速民機特有的,相比于亞聲速民機,設計難度和工作量顯著增加。因此,超聲速民機的設計工作非常需要理論方法的指導,特別是在概念設計中需要有快速有效的計算方法。

在超聲速民機概念設計階段,關于聲爆計算的理論方法寥寥可數,標準聲爆理論和聲爆最小化方法是最重要的兩個理論方法。如果有一個初始構型,在給定的約束條件下可以通過構型參數優(yōu)化設計來尋得一個最低的聲爆,這是正向設計,但初始構型對優(yōu)化解影響很大,有些構型即使經過優(yōu)化也可能達不到預期的聲爆設計要求。當前比較成熟的方法是反向設計的方法,即在初始構型基礎上,采用中場聲爆最小化方法,即JSGD理論[2],確定等效飛機截面積,以此為約束迭代得到飛機構型,中場聲爆最小化方法基于Whitham的聲爆修正線性理論[8-9],因此該方法假定近場非線性較弱。盡管標準聲爆理論和中場聲爆最小化方法有弱非線性假定的局限,但是這兩個理論方法分別給出了詮釋聲爆現象、減小聲爆策略的數學公式,并且在應用計算中簡單快速。它們是超聲速民機概念設計中基本的理論和方法,在理論上具有重要意義,在概念設計中也有實用價值,因此,我們需要對其有全面深入的認識。本文主要對這兩個理論方法及應用進行了評述和展望。

1 聲爆的理論和預測方法

1.1 Whitham修正線性理論及標準聲爆理論

Whitham修正線性理論[8-9]不僅是標準聲爆理論及預測方法的基礎,而且也是中場聲爆最小化方法的基礎。因此,本節(jié)先對該理論做一個概述。在Whitham的修正線性理論基礎上,20世紀60、70年代形成了標準的聲爆理論[10],隨后為了描述機動飛行以及大氣邊界層中聲波的復雜變化,聲爆理論進一步被細化和完善,并形成了在概念設計中應用的聲爆預測方法。修正的線性聲爆預測理論,雖有局限性,但快速有效,拓展后可處理許多實際復雜的情況,在多學科多目標優(yōu)化概念設計中很有用。

Whitham的修正線性理論有兩個表述,一個基于飛機坐標系[8],另一個基于地面坐標系[9]。下面分別簡要介紹。在飛機坐標系下,針對均勻大氣中的無升力細長旋成體,Whitham(1952)修正線性理論的主要步驟是:首先求出小擾動線化勢流方程的解(式1),定義F函數(式2),它給出了擾動解與旋成體橫截面面積的關系。在同一半徑r處,聲壓與F函數成正比,聲壓形狀與F函數形狀相似。然后修正聲速,因為小擾動下聲速是常數,特征線是平行的直線,不能形成激波,因此需要修正。Whitham的做法是假設經過旋成體軸向一點的近似特征線(直線)上的解是過該同一點的準確特征線(曲線)上的解。這個修正的解并不是原非線性方程的精確解,但是結果表明這樣的處理可以較好地描述弱非線性效應[10-11]。最后,激波的切線方向假設為兩條相交特征線的角平分線,旋成體頭部某區(qū)域內所有正過壓形成了N波的頭激波,即對應的特征線匯聚,擾動疊加求得頭激波強度(式3)。詳細推導還可參見中文文獻[12]。

Walkden[13]借用超聲速面積律(area rule)的波阻分析方法將上述Whitham的理論推廣到翼身組合升力構型的情形。將F函數中S換成等效橫截面面積Se,Se＝SV＋S L,體積貢獻的橫截面面積(SV)與升力貢獻的橫截面面積(S L)之和,這相當于將飛機等效為一個旋成體。體積貢獻的橫截面面積(SV)由該處與馬赫錐相切的平面切出的截面在軸向投影而得到,這與超聲速面積律中的處理是一致的。

對于在均勻大氣中勻速飛行的情形,采用上述Whitham的理論[8]可以方便求得遠場地面上N波(通常還要乘以地面反射系數1.9～2.0),而對于非均勻大氣或機動飛行的情形,上述方法很麻煩。簡便的方法是采用地面坐標系下的射線尋跡(ray tracing)方法,例如 Whitham基于射線的修正線性理論[9],Plotkin[10]稱其為 Whitham's Rule。下面簡要介紹該理論。

基于射線Whitham重新闡述了修正線性理論并給出相應的計算公式[9]。線性理論的解可給出一階精度的波幅,但是聲波的形狀(或射線到達時間,或特征線位置)僅是零階精度,為了獲得一致的一階精度,需要修正聲波的傳播速度即聲速,或者說,盡管聲速變化很小以及由此導致聲波的形狀改變很小,但傳播足夠遠的距離后,聲波的形狀改變會很大甚至產生激波,因此需要修正聲速以描述波的非線性變形。在地面坐標系下,無風情形的聲波過壓為式(4),與式(1)形式上相同,由于采用不同坐標系,它們的自變量不同。

式中,t是波前到達s處的時間,τ是波前的相位,s是波前沿著聲線傳播的距離,B是s的函數,反映幅值的變化。如果是非均勻大氣,式(5)中聲速a需替換為a0＋δa＋δu,進一步可得:

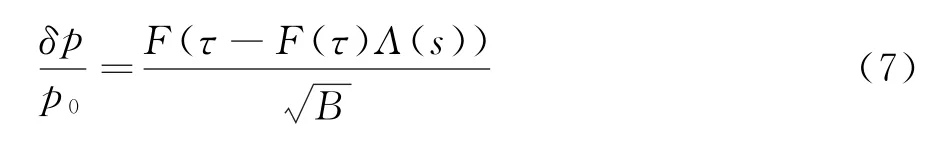
式(7)表明相位為τ的波前到達s處的提前時間是F(τ)Λ(s)。

非線性變形的壓強信號上每點提前F(τ)Λ(s),激波位置由面積平衡(area balance)確定(圖1),這指的是激波位置將聲壓信號劃分成面積相等的兩部分。這等價于兩條相交特征線的角平分線即是激波的切線方向,因為線化的激波速度等于該激波前后等熵波速度的平均值[10]。

設T(s)是在s處剛好形成激波的波前的相位,由式(6)可得

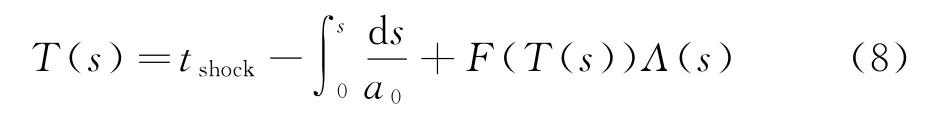
式中tshock是在s處形成激波的時間,上式對s求導,dtshock/ds即是激波速度的倒數,再由Rankine-Hugoniot關系式的1階近似可得線化的激波速度U s,可求得

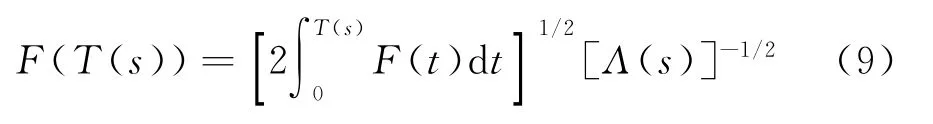
上式給出激波后的F函數,因此也就給出了激波后過壓,即

激波位置可通過麻煩的迭代計算得到,Middleton[15]和Hayes[16]分別給出了一般性的算法。特例,在遠場形成N波,此時T(s)→τ0,這里F(τ0)＝0。

前面討論了基于射線的修正線性理論,下面簡要介紹射線尋跡法。假設大氣聲速a0和密度ρ0是變化的,聲壓信號的波長遠小于大氣梯度的長度尺度,無風速情形下由聲壓信號波動方程可以推導得出,

式中n是射線單位方向向量,與波前函數正交,其中ρ0a0是聲阻抗是單位時間內通過垂直于聲傳播方向的單位面積上的平均聲能量,這就意味著能量守恒。定義射線管為許多射線的集合,類似于流管。沿著射線管積分得:

其中A是射線管面積。數值計算時要考慮每個微小的射線管面積。

Plotkin[10]總結利用射線求解聲爆的標準過程是:第1步,根據線化的面積律計算飛機的初始聲源信號,由此得到Whitham的F函數(聲源確定)；第2步,初始的某一射線的方位由飛機的位置和航跡確定,隨著時間推進計算該射線的方位及射線管面積,根據Blokhintzev不變量,由近場聲壓幅值求出中場(或遠場)某處聲壓幅值,此處聲波信號的形狀仍與近場聲波信號形狀相同,只是幅值改變(聲壓傳播)；第3步,計算每點的提前量F(τ)Λ(s),出現多值點時,采用面積平衡確定激波位置,然后由激波后過壓公式計算激波強度(計算激波)。上述標準聲爆預測計算流程概況為圖2。

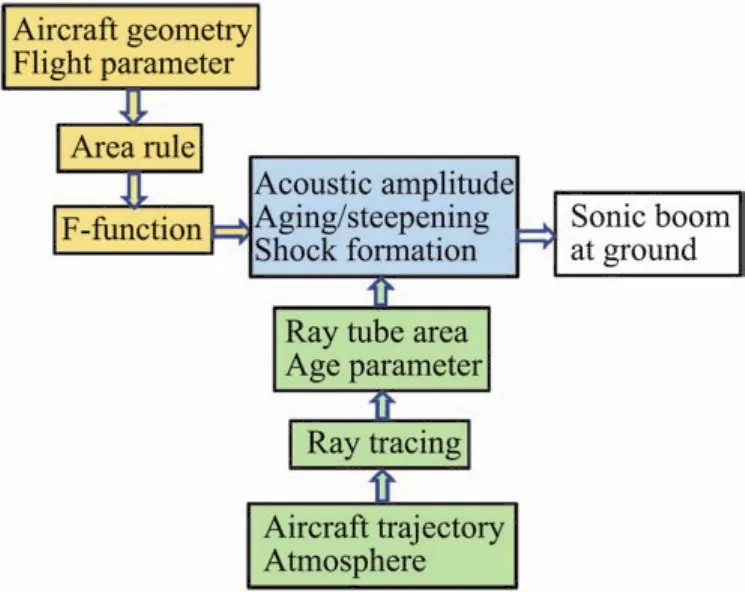
圖2 標準聲爆理論的計算流程,改自Maglieri[14]Fig.2 Flow chart of standard sonic boom theory[14]

1.2 聲爆預測方法評述

聲爆預測方法一般由兩部分組成,一部分是聲源的計算,另一部分是聲信號的傳播。每一部分都有若干種處理方法,由此形成各種聲爆預測方法。如果以聲信號傳播算法不同來區(qū)別,主要的聲爆預測方法有以下四種。一是標準的聲爆預測方法,如上節(jié)圖2所示,它以F函數為核心,先由飛機幾何及飛行參數,結合面積律求出F函數,即得到聲源,然后利用射線尋跡,由聲壓信號非線性變形計算激波位置,由激波后F函數得到聲爆。在該方法的基礎上,計及特殊飛行狀態(tài)而形成的軟件有,ARAP[16]；TRAP[17]。第二種是Thomas(1972)提出的波形參數法(waveform parameter method)[18],它不以F函數為核心,而是直接處理聲壓信號,即把聲壓信號分段,用若干參數描述,計算每段信號的傳播得到聲爆。該方法不依賴F函數,可以利用CFD或實驗得到近場聲壓。因此,波形參數法適用性更廣,在許多項目中得到應用。例如該方法被Plotkin拓展到處理匯聚的聲爆,形成了FOBOOM[19],并被美國空軍應用為BOOMAP2；Plotkin進一步開發(fā)了SBORT[20],計算速度提升了1-2個量級,并被美國空軍應用為BOOMAP3；Plotkin在FOBOOM和SBORT基礎上為美國空軍開發(fā)了PCBoom3[21],該軟件發(fā)展到PCBoom6.6[22]。第三種方法也不依賴于F函數,而是采用非線性Burgers方程計算聲壓的演化傳播,并在方程中加入吸收項、分子弛豫項、大氣分層項等,這稱為增廣(Augmented)Burgers方程。例如Rallabhandi[23]為NASA開發(fā)了sBOOM,其中壓強信號傳播采用了增廣Burgers方程。第四種方法采用Khokhlov-Zabolotskaya-Kuznetsov(KZK)方程[24-27],相比于增廣Burgers方程,增加考慮了衍射、軸向/橫向對流等三維效應的影響,KZK方程是三維的,計算量更大。

第一種方法無論聲源計算還是聲壓信號傳播都以F函數為核心,這意味著非線性較強時會使計算準確性大打折扣,但是該方法計算效率高,在非線性較弱時可以得到比較準確的結果。后三種方法的模型復雜性依次增加,計算量也逐漸增大,但是這三種方法不依賴F函數,適用于非線性較強的情形,可從更準確的近場聲壓出發(fā)計算聲爆。

國內學者應用波形參數法的較多[28-31],為了計及更復雜的大氣影響,也開始有研究增廣Burgers方程的工作[32]。

經過近60年的發(fā)展,國外已經有成熟的聲爆預測方法和軟件以及開展了系統的風洞實驗和飛行驗證試驗[14,33]。具有一定準確度、高效率的聲爆預測方法是概念設計階段必不可少的。我們不僅要掌握已有聲爆預測方法的原理,更要著重調研相關的風洞實驗和飛行試驗結果,經過校驗的預測方法才能更好地應用于概念設計。

2 聲爆最小化方法及應用范例

2.1 聲爆最小化方法的代表——JSGD理論

在前述標準聲爆理論基礎上,20世紀60、70年代發(fā)展了聲爆最小化方法,現在也稱為Jones-Seebass-George-Darden理論(JSGD或SGD理論)[1]。Rallabhandi和Plotkin等[34-36]進一步發(fā)展了該理論。聲爆最小化方法構成了當前低聲爆構型概念設計的基礎。下面簡要介紹聲爆最小化方法及其發(fā)展。

對于足夠光滑細長體型的飛機,產生的等熵壓縮波在遠場最終匯聚形成N波。Jones[37]證明了遠場的激波強度的下限對應于飛機頭部鈍化,相應的F(x＝0)為Delta函數,這樣的近場信號很快就形成N波,根據式(3),激波強度按照r－3/4衰減,快于如式(1)按照r－1/2衰減的柱波。Mc Lean[38]指出在爬升階段,聲信號達到地面時還沒有形成N波。隨后許多研究者指出甚至在巡航階段,足夠光滑細長的大型飛機,其聲信號達到地面時可能也沒有形成N波。Hayes[39]指出在真實大氣中,特征線相比于均勻大氣的情形匯聚得更慢。這樣,中場信號就可能出現在地面處(所謂中場信號,通常位于數倍飛機長度距離之外,其形狀依賴于飛機構形并隨離開飛機的距離變化而改變；遠場信號形狀不再隨離開飛機的距離變化而改變)。如果地面處為中場信號,則還含有F函數的信息,設計合適的F函數,即相應地改變飛機形狀,就可以有效減小地面處聲爆。對于中場信號Seebass[40]和George[41]指出頭激波強度的下限同樣要求F(x＝0)為Delta函數。George和Seebass[42-43]發(fā)展了一個完整的理論來使頭激波和尾激波最小化,這個理論成為聲爆最小化方法的基礎。

這里先只考慮地面信號(實際為中場信號時)的頭激波[41],以一簡單情形為例來說明。如果要使地面處最大過壓最小化,就要重新定義F函數,F(y)＝F1(y)＋F2(y),其中F1＝δ(y),Delta函數(即Jones的F函數),F2是添加的部分,對應AEy0O(圖3),AE段F2為常數,由式(2)表明此段S″e＝0,即此段等效橫截面面積S e＝常數,因此這一段過壓也為常數(由式(1)可知)。在給定體積和升力的前提下,添加F2(AEy0O),意味著要相應減小F1的面積,因此就減小了地面處頭激波強度,即減小了最大過壓P s0,在地面形成平頂型(flat-top)信號(圖3)。

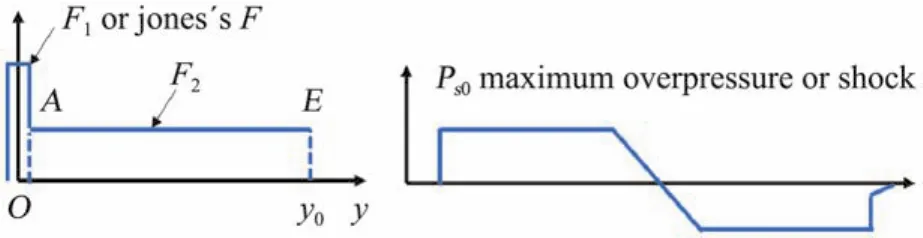
圖3 F函數及對應的平頂型信號Fig.3 F function and pressure signature of flat-top type

AE段F2也可以不為常數,而是線性增長(圖4),此部分對應著擾動波的壓縮,只要在地面(實際為中場)該部分的壓縮不形成激波,此時對應有一個從頭激波P s到最大過壓Pmax的提升時間τ,在地面形成斜坡型(ramp)信號(圖4),通過調節(jié)F2使頭激波最小。

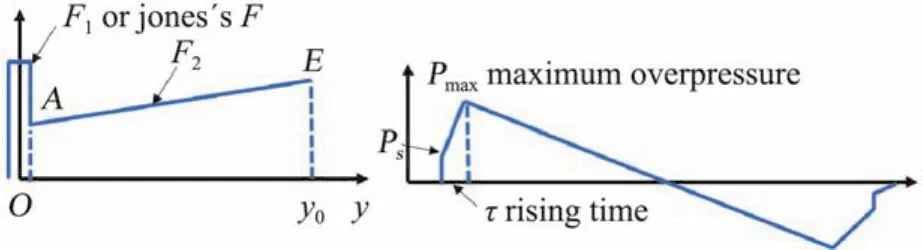
圖4 F函數及對應的斜坡型信號Fig.4 F function and pressure signature of ramp type

飛機頭部鈍化可使該構型的聲爆最小,但是此時頭部弓形激波導致的激波阻力很大,相比較,細尖的頭部在近場只產生等熵壓縮波,此時阻力小,但是遠場壓縮波匯聚成激波,聲爆大。為了兼顧阻力和聲爆,Darden[44-45]拓展了前述Seebass-George聲爆最小化理論[42-43],去除了其中頭部鈍化限制(文獻中簡稱SGD理論或JSGD理論)。此時F函數表示成

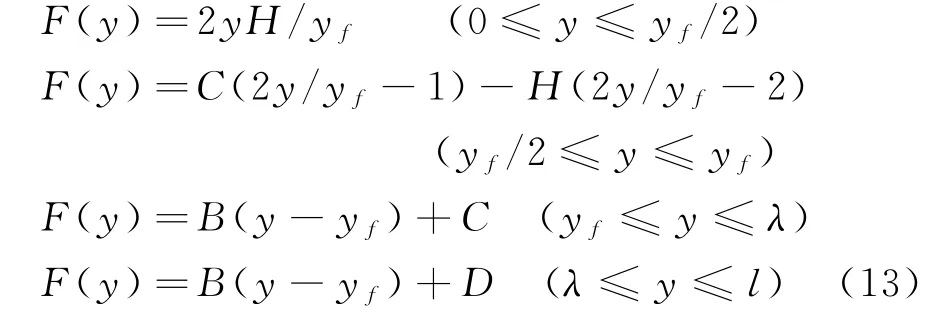
F函數在頭部不再是Delta函數,而換成尖錐狀(spike)函數(圖5),去除了鈍化限制。圖5中,H是尖錐的高度,y f是尖錐寬度或前部面積平衡點,y r是后部面積平衡點,λ是F函數小于零的起始點軸向坐標,l是飛機等效長度。由聲爆最小化計算出F函數,然后就得到等效截面面積分布S e:

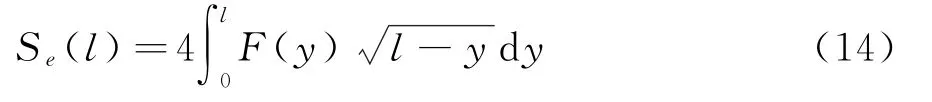
F(y＞l)可以采用Petty[46]的方法(假定尾流面積為常數)給出。

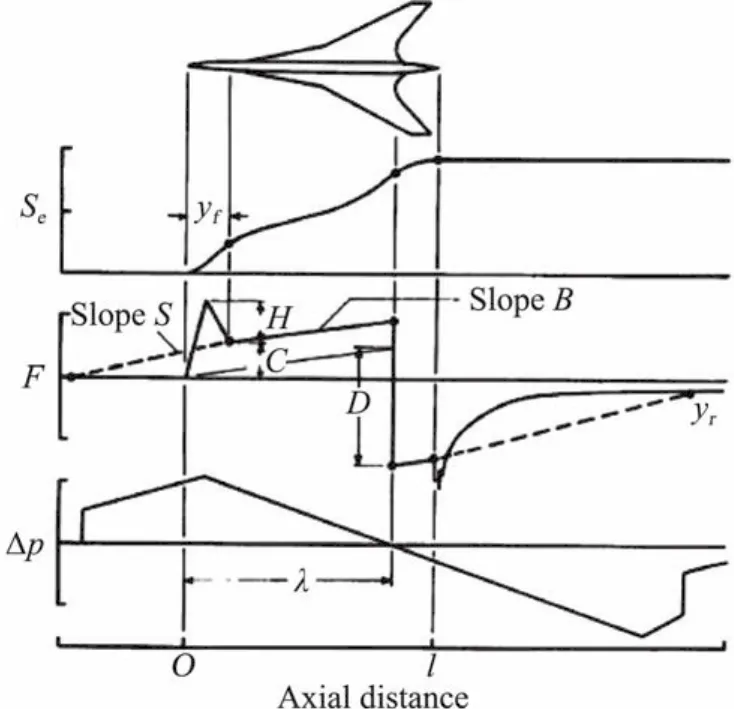
圖5 Darden的F函數及對應的有效橫截面和ramp型信號Fig.5 Darden's F function and pressure signature(picture from Darden[44])

當頭部很鈍,面積分布有無窮大梯度,F函數是Delta函數,即y f＝0時激波強度最小。由式(3)可知頭激波強度與F函數曲線下方(F＞0)的面積成正比。隨著y f增加,F函數尖峰下的面積增加,激波強度也就增加了。例如,某型飛機Δp(y f/l＝0.2)是Δp(y f/l＝0)的1.2倍左右[45]。

利用JSGD理論的設計過程是通過設計合適的F函數,即以F函數中的參數作為優(yōu)化變量,使地面信號滿足設定的平頂型或斜坡型,由得到F函數計算出等效截面面積S e分布,以S e為約束迭代計算出外形。

前述F函數在表示后部信號時存在局限性,因為飛機后部有發(fā)動機及尾翼,比較復雜,文獻[34-36]改進了F函數,峰值不再固定在y f/2處,F函數中的幾個坡度細分為更多段,增加設計靈活性,以適應同時滿足聲爆信號參數及其它性能參數,特別是使響度最小。Rallabhandi[47,34]提出一種高效的兩步偽反設計優(yōu)化方法(bilevel pseudoinverse optimization),第一步,設計變量是改進的F函數中的參數,地面信號響度最小為優(yōu)化目標,用遺傳算法得到優(yōu)化的等效截面面積S e分布；第二步,設計變量是外形參數,以前一步得到S e分布為優(yōu)化目標,用遺傳算法計算出優(yōu)化的外形參數。

飛機等效截面的改變對地面信號影響很大,如果要對比低保真度和高保真度兩種設計方法,這兩種方法都需要基于準確的外形數據以便比較[47,48]。Colonno和Alonso[49]在前述工作基礎上研究了輸入參數不確定性對地面信號不確定性的影響。

2.2 JSGD理論應用范例

以JSGD理論為代表的聲爆最小化方法通過設計合適的F函數,可設定聲爆形狀(shaped sonic boom or shaped boom),并在一定約束條件下使聲爆盡可能小。這里列舉兩個典型的應用JSGD理論的例子。第一個例子是AFRL/NASA以F-5E為飛行平臺開展的聲爆形狀設定的驗證(Shaped Sonic Boom Demonstration,SSBD)[3-4]。SSBD目標是驗證源于JSGD理論的低音爆飛機外形設計方法,采用前體修型的F-5E進行飛行驗證[4]。F-5E SSBD外形的特點:前體鈍化,飛機前體長度增加,發(fā)動機進氣口和機翼距離前端更遠。在近場,鈍化的頭部形成較強的弓形激波,后面跟隨著一些較弱的激波,這些弱激波的速度低于弓形激波的,而且它們間隔較遠,它們在到達地面時還未匯聚,由此減小聲爆,參見圖6。F-5E的聲爆初始過壓約為1.3psf,響度約為102 PLdB,聲爆水平很高,依據JSGD理論前體修型的F-5E SSBD實現了平頂型地面信號,初始過壓降到0.7 psf左右 (圖7)。飛行驗證試驗表明地面聲爆信號是可以計算預測的(圖8的理論計算結果與圖7的飛行實驗地面測試結果非常接近),同時,表明了利用JSGD理論修改飛機外形實現低聲爆設計是可行的。F-5E等效截面中容積占比大大高于低音爆構型(比如HSCT),因此,F-5E SSBD前部修型改變非常大以實現較為合適的地面信號。這說明JSGD理論非常依賴于初始構型,如果初始構型太差,就很難進一步降低聲爆水平,因為基于JSGD理論的幾何修型還要受到其它約束條件的限制。

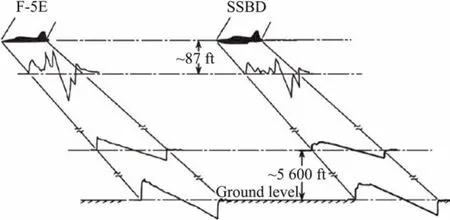
圖6 F-5E和F-5E SSBD的壓強信號演化Fig.6 Pressure signatures of F-5E and SSBD(picture from Maglieri[14])

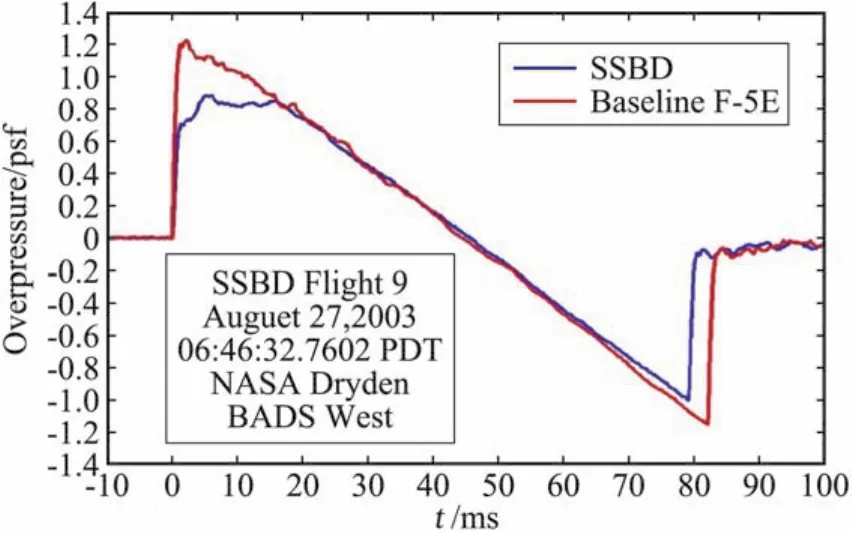
圖7 F-5E和F-5E-SSBD飛行測試的地面壓強信號Fig.7 Ground pressure signatures of F-5E and SSBD from flight test(picture from Pawlowski[4])

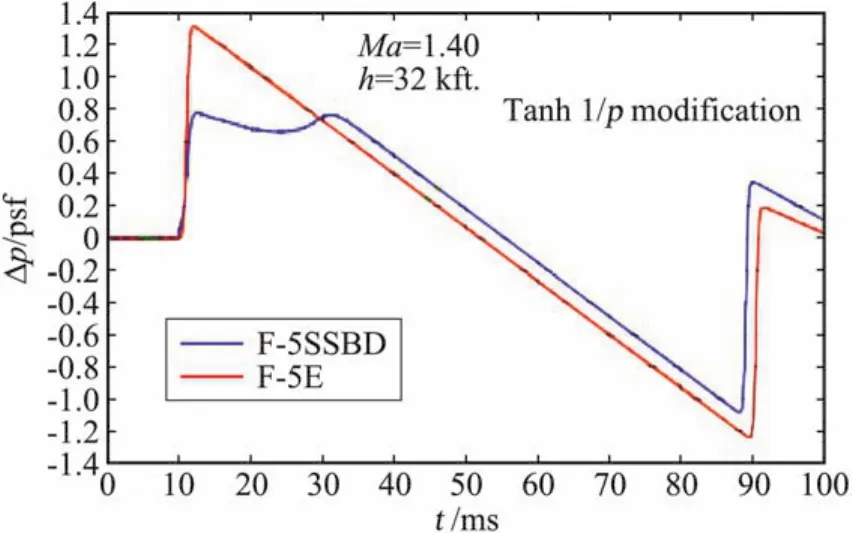
圖8 F-5E和F-5E-SSBD理論計算的地面壓強信號Fig.8 Ground pressure signatures of F-5E and SSBD from simulations(picture from Pawlowski[4])

第二個例子來自洛馬的N＋2小型超聲速民機驗證項目。首先要提一下,在對公眾聲爆接受度的研究中,Leatherwood等[50-51]發(fā)現聲爆的頻譜特性更重要,采用感覺噪聲級比單純用聲爆初始過壓、最大過壓、提升時間等參數更可靠。因此,洛馬研究團隊為了使響度最小化,設定了一種由多個小激波構成的斜坡型聲爆信號(multi-shock ramp signature),見圖9,它比圖4所示的斜坡型信號復雜,通過調整激波間隔時間,在聲壓等效的情況下,可以得到更小的響度[52]。

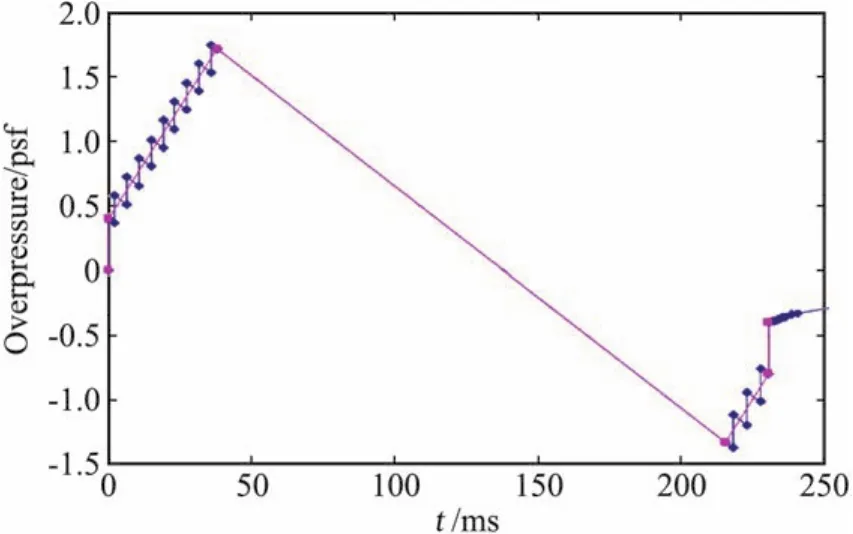
圖9 斜坡型和等效的多激波斜坡型壓強信號Fig.9 Ramp and equivalent multi-shock signatures(picture from Morgenstern[52])

洛馬N＋2第1階段和第2階段都應用了JSGD理論,第2階段是以第1階段的LM1021為初始構型,但是只采用JSGD理論,在飛行軌跡外(offtrack)±40°處聲爆信號沒有明顯改善。這是因為初始構型LM1021機翼和V型尾翼之間的膨脹波強度難以減弱,對應升力有較大的間斷。由此可見,JSGD理論受到初始構型的約束,難以進一步改善聲爆信號。因此,洛馬對LM1021的后體重新設計得到LM1044。洛馬N＋2第2階段LM1044的結果表明,整個聲爆毯(巡航開始階段)最大聲爆小于85PLdB,平均聲爆比第1階段LM1021降低了4PLd B[53]。計及大氣吸收和分子弛豫情況下,LM1044巡航全程平均響度79PLd B,若再計及湍流影響,大致為74PLdB,這仍然未達到NASA N＋2代超聲速民機70PLd B目標。實現NASA 3代超聲速民機的聲爆指標是一個具有相當挑戰(zhàn)性的工作。洛馬兩個階段的工作表明,聲爆最小化方法的應用效果受制于初始的布局構型,當應用該方法達不到設計目標時,不得不重新考慮初始的布局構型設計。初始布局構型設計相當關鍵。

JSGD理論用到Whitham的修正線化理論,只在1.2＜Ma＜3范圍有效,而在跨聲速0.9＜Ma＜1.15范圍近場高度非線性(聲速線對外形敏感),當Ma＞3時近場也有了明顯的非線性現象(出現強激波),這些非線性情形(盡管仍是小擾動)通常需要用CFD計算。由于這些非線性,聲爆最小化方法,由地面信號計算其所對應的等效面積分布就沒有唯一性,這時需要采用迭代的方法[54-55]。

對于小擾動但有明顯非線性或大擾動強非線性的情形,上述聲爆最小化方法不適用,此時可采用近場壓強信號最小化方法,即近場(一般在3-4倍參考長度處)的壓強場通過求解可壓的Euler方程得到,也可以通過風洞實驗測得,采用遺傳算法對飛機外形進行優(yōu)化,優(yōu)化目標是近場激波強度達到最小[56,57],近場信號到地面的傳播是求解增廣Burgers方程。如果采用的是風洞模型的測試數據或該模型的CFD計算數據,則需要考慮從小尺度模型到全尺寸的變換,然后才可由傳播算法計算出全尺寸飛行器的地面聲爆。

國內一些學者在上述方面也開展了工作,比如,馮曉強等[58]應用JSGD理論嘗試設計了一種超聲速客機。馮曉強等[59]應用了改進的JSGD理論,采用遺傳算法,以超壓值和有效容積為優(yōu)化目標。喬建領等[60]研究了一種代理優(yōu)化方法在低音爆設計中的應用,表明其效率高于遺傳算法,優(yōu)化結果好于梯度法。

聲爆最小化方法的物理思想是,在機頭保持一個足夠強的弓形激波,后面跟隨的較弱的激波追不上前面的弓形激波,不會產生匯聚,但是這個頭部的弓形激波較強,也不利于進一步減小聲爆。為了進一步減小頭部激波同時防止激波匯聚,灣流公司(Gulfstream Aerospace)開發(fā)了創(chuàng)新性的靜音錐技術(Quite SpikeTM),在飛機頭部加裝靜音錐(可伸縮、非軸對稱、略向下偏離重心水平線),靜音錐每一級的膨脹波使下一級的激波變弱,弱激波互相平行,同時機頭處的激波也減弱了,這樣就不會在遠場匯聚成強激波。在F-15B Quite Spike項目中靜音錐安裝在F-15B上進行了飛行試驗以驗證靜音錐結構系統的可行性,并測量了近場壓強信號以驗證CFD計算結果[61-62]。加裝靜音錐還有一個好處,保證飛機前部有足夠的容積,這是低聲爆公務機設計難點,因為減小頭部激波通常意味著要減小機身前部的等效截面面積。Howe[63]針對灣流公司QSJ構型的遠場計算結果是,2級的靜音錐可以將地面頭激波從0.4 psf(無靜音錐)降到0.15psf。國內沈沉等[64]也開展了靜音錐的數值研究工作。

綜上,基于JSGD理論的低聲爆設計方法是可行的,在某一基準構形下,通過JSGD理論設計合適的F函數可以使聲爆進一步減小,但無法給出可能存在的更低聲爆外形,而通過外形布局的巧妙設計,比如灣流公司的靜音錐,洛馬的LM1044,就獲得了更低的聲爆。還有一些未經過充分驗證的非常規(guī)布局,比如,類似于Busemann的上下雙翼構型[65],利用激波和膨脹波之間的干擾以減弱激波強度。更多的通過外形布局設計減小聲爆的構想可參考Maglieri的綜述文章[14]。

3 總結與展望

本文先介紹了Whitham修正線性理論的兩種表述的主要思想和公式,這是標準聲爆理論和聲爆最小化方法的基礎,然后評述了在概念設計中聲爆預測的幾種方法及應用,接著介紹了低聲爆構型概念設計的重要方法——聲爆最小化方法,以及該方法應用的兩個典型例子。

1)標準聲爆理論中的F函數建立了飛機橫截面積與聲壓以及聲爆之間的關聯,聲爆最小化方法給出了設計合適的F函數以達到盡可能小的聲爆的策略。已有工作表明聲爆理論和最小化方法是有效的。

2)聲爆最小化方法的應用效果受制于初始的布局構型,當應用該方法不能達到設計目標時,也許不得不嘗試修改初始的布局構型,甚至多次修型迭代。初始布局構型的設計非常關鍵。

當前超聲速民機有一些主要的設計目標,在概念設計中存在著特有的難以兼顧的矛盾,這大大增加了設計難度和工作量。解決途徑是發(fā)展專門針對超聲速民機的多學科多目標優(yōu)化設計方法,其中,標準聲爆理論和最小化方法是組成該設計方法的重要基石。聲爆最小化方法是針對聲爆這個唯一目標的,實際應用中僅僅依靠聲爆最小化方法通常難以滿足設計要求,亟需進一步研究可以有效地兼顧聲爆/阻力等多目標參數的理論和方法。