SAS與PANS模型在圓柱繞流中的應用比較

劉 躍管小榮徐 誠

(南京理工大學 機械工程學院,南京 210094)

0 引 言

廣泛存在于航空航天、風工程等空氣動力學領域的鈍體繞流問題通常為無序、非線性、多尺度的湍流分離運動,在使用數值模擬方法(CFD)對其進行分析計算時,湍流的求解成為影響CFD計算精度的瓶頸問題[1]。在諸多的湍流模型中,兼顧計算精度與資源消耗的RANS/LES混合方法受到人們的青睞[2],混合模型在近壁區及遠場使用RANS模型,而在分離區及尾跡區切換為更合理的類LES濾波模型,極大地提高了計算精度,且資源消耗遠小于LES僅略大于RANS。近年來,不同學者發展了種類繁多的混合方法,其中包括DES(Detached Eddy Simulation)方法[3]、SAS(Scale Adaptive Simulation)方 法[4-7]、PANS(Partially Averaged Navier-Stokes)方法[8]、PITM(Partially Integrated Transport Model)方法、LNS(Limited Numerical Scales)方法等。其中DES方法是最早出現的混合方法,經過一系列改進(DDES、IDDES)已發展較為成熟[9-13]；SAS模型為能夠解析寬頻非定常湍流脈動而對計算網格依賴較小的新一代非定常湍流預測方法(URANS),通過加入參照當地流動的馮卡門(von Karman)長度尺度L vk,合理地釋放更多流場信息[14-15]；PANS模型同樣是最近發展的一種RANS-DNS橋接模型,模型構造相對簡單,通過加入模化湍動能比例參數f k調整湍流的模化量來調整湍流求解尺度[16]；DES模型的提出者Spalart在2000年時曾預測,2045年左右計算機的計算能力才能滿足利用LES解決90%的湍流問題,因此,在現階段,驗證與發展RANS/LES方法仍是非常必要的[17-18]。

鈍體繞流中的圓柱繞流計算模型簡單,同時又包含如湍流壁面、剪切層失穩、流動分離、周期性渦脫落等豐富的流動現象,是考察湍流模型計算性能的標準算例。Re＝3900的圓柱繞流是典型的亞臨界雷諾數流動,流動結構復雜且耗費資源較少,人們對該雷諾數的圓柱繞流進行了大量的實驗[19-22]及數值研究[23-29],有可靠豐富的數據可供參考。本文選用SAS模型及兩種變f k構造函數的PANS模型計算了Re＝3900的圓柱繞流流場,并重點從流場特征捕捉、氣動力特性計算、渦黏性控制等方面對SAS模型及PANS模型進行了比較,通過對比標準網格與加密網格后的計算結果,比較了兩類混合方法對網格的適應性,并探討了兩類混合模型的尺度函數對流場的調控機制。

1 計算模型及數值方法

1.1 控制方程

控制方程為三維N-S方程,在一般計算坐標系(τ,ξ,η,ζ)下的 守恒形 式為:

式中:為守恒變量為無粘通量為黏性通量,各物理量的具體表述參見文獻[1]。

1.2 湍流模型

1.2.1 SST-k-ω模型

SST模型由標準k-ω模型與k-ε模型混合修改而成,該模型兼顧了k-ω模型的近壁性能及k-ε模型的遠場準確性,SST模型中湍動能k和比耗散率ω的輸運方程可表示如下:

式中模型參數σk、α、β、σω、σω2均由對應的k-ω模型參數φ1和k-ε模型參數φ2通過一定函數計算得到,其對應的函數關系為:

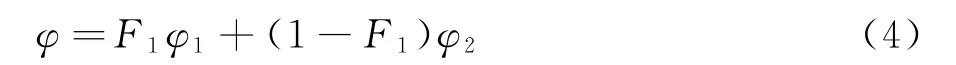
SST模型中湍動黏度μt可表示為:

式中S為應變率張量S ij的模,SST模型中F1、F2函數構造方式及各模型參數值參考文獻[30]。

1.2.2 SST-SAS模型

尺度自適應SAS(Scale-Adaptive Simulation)模型是一種較新的創新型湍流模型,它通過在湍流模型中加入刻畫當地流動拓撲的von Karman長度尺度L vk來作為湍流模型的第二長度尺度[6]。基于SST模型的SAS模型構造方法為在式(3)SST模型的ω方程中加入發揮自適應作用的源項QSAS,其定義式為:

由式(6)可以看出:在SAS模型中出現了由一階及二階速度導數決定的長度尺度項L vk,該長度尺度基于當地流動而與網格尺度無關,在湍流邊界層內,L vk能模化慣性子區所有湍流脈動,同時,在非穩態區域L vk能根據當地網格分辨的湍流渦動態調整RANS長度尺度。在SAS模型中,湍動黏度μt仍按照式(5)計算。

1.2.3 SST-PANS模型

本文中所用PANS模型同樣是基于SST模型修改而成[8],其原理是在SST模型中引入兩個模型控制參數f k和fω:

式中:f k為模化湍動能與總的湍動能之比,fω是模化比耗散率與總的比耗散率的比值。如果假定f k和fω是不隨時間和空間變化的常數,則k和ω的輸運方程(2)、(3)變為:

將式(8)、(9)與式(2)、(3)對比可以發現在PANS模型中主要是模型參數發生了變化,PANS模型中模型參數σku、σωu、σω2u、β表示為:

通過以上變化,將SST模型轉變為SST-PANS模型,由k、ε、ω的關系可得式(10)中fω與f k和fε的關系,在SST-PANS模型中,fε一般取為1,這樣PANS中的參數可以表示為f k的函數。通過調節f k的值(1-0),改變模化的湍動能與比耗散率的比值,從而實現RANS-DNS的轉化。這時湍動黏度μtu變為:

在早期PANS模型的應用中,f k通常被設置為空間常數,通過計算發現對于整個流場很難確定合適統一的f k值。對于復雜的分離流動問題,計算時分離區與尾跡區需要較小的f k值(f k＜1)釋放湍流信息,而近壁區與遠場區采用RANS模型(f k＝1)更合理,因此近年來人們逐漸嘗試用適當的函數來計算f k分布,本文選取其中兩種相對簡單、計算相對穩定的變f k函數來進行對比。

(a)類DES型f k函數[31-32]。該函數參考DES模型中模型尺度的構造方法,將f k表示為網格尺度Δ與湍流尺度L u的函數:

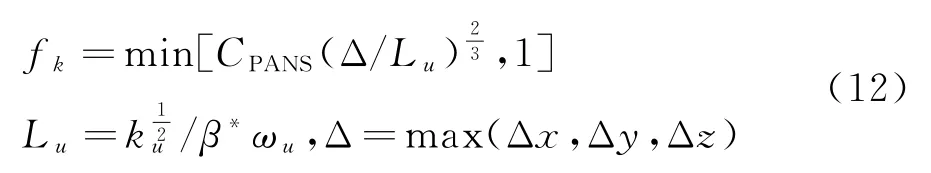
式中模型常數CPANS取0.3。用該函數進行計算時,在分離區與尾跡區,網格尺度要小于湍流尺度,因此f k＜1；在壁面及遠場區域,網格尺度大于湍流尺度,因此f k＝1。文中將使用類DES型f k分布函數的PANS模型稱為PANS(des)模型。

(b)Tanh型f k函數[33]。在該函數中,f k可表示為:

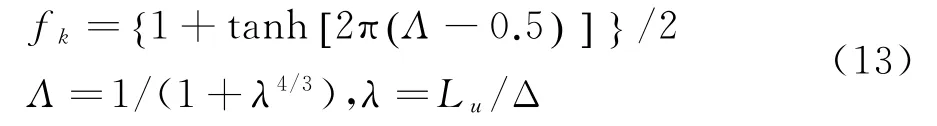
對比式(12)與式(13)可知,Tanh型f k函數由湍流尺度、網格尺度及tanh函數修改而成,tanh函數的取值范圍為(-1,1),這樣根據流動與網格關系得到不同位置的f k取值范圍為(0,1)。文中將使用Tanh型f k函數的PANS模型稱為PANS(tanh)模型。

2 計算模型及數值方法

2.1 計算域、網格及邊界設置

文中圓柱繞流計算雷諾數為Re＝3900(基于圓柱直徑D與遠場來流速度U∞),圖1為計算域及邊界條件示意圖。為減小上游來流對計算的影響并使尾跡區流動充分發展,上游來流區域(x方向)及橫向區域(y方向)延展至20D,下游計算區域設置為30D。根據近尾跡區流向結構的展向波長設置計算域展向長度(z方向)為πD[2]。圓柱體設置為無滑移壁面,上游入口流動各物理量由無擾動自由來流條件給定,下游出口設置為無反射邊界,計算域的上下界面設置為自由滑移壁面,計算域的前后邊界設置為周期邊界。文中坐標系設置如圖1右下角所示,軸向從上游到下游方向為x正方向,坐標系符合右手螺旋法則,橫向為y方向,展向為z方向,方位角從上游圓柱前駐點為0°開始,順時針旋轉為壁面方位角θ的正方向,下游背風點為180°。

圖1 計算域及邊界條件Fig.1 Computational domain and boundary conditions

圖2為圓柱繞流的局部網格示意,計算網格為分塊結構化網格。為了保證計算精度,在壁面附近及尾跡分離區域對網格進行適當加密,壁面第一層網格高度為0.002D,保證壁面y＋＜1。為了探討不同模型的尺度函數對網格的敏感性,文中設置了兩套計算網格,其中標準網格保證近壁增長率為1.06,分離區網格固定為0.1D；加密網格為保證近壁增長率為1.04,分離區網格固定為0.05D。參考文獻[24,25]中的網格設置見表1。

圖2 圓柱繞流局部網格Fig.2 Computational grid for the cylinder

表1 計算網格Table 1 Computational grids

2.2 方程求解設置

文中對所求方程組空間離散采用有限體積法(FVM),對流項中速度項的離散采用三階限制(TVD)中心差分格式,湍流項離散采用二階限制中心差分格式,梯度項及黏性項的離散采用四階中心差分格式,壓力與速度耦合選用PISO算法。為了保證計算的收斂性及穩定性,時間項離散采用二階隱式后退歐拉(Backward)格式,并采用自適應時間步長方法[24],時間步長設置為庫朗數(Courant number)小于0.5,并且保證在一個渦脫落周期內包含近500個時間步。

3 計算結果分析

3.1 數據采集及流場宏觀結構

文中分別計算了SST、SAS、PANS(des)、PANS(tanh)模型的圓柱繞流流場。周期性渦脫落是該計算雷諾數下的顯著特征。為了獲得合理的統計數據,根據Franke等[34]的研究結果,圓柱繞流的統計周期應大于40個脫落周期。因此參照文獻[34,25],本文中總的計算時間約為60個渦脫落周期,在對非定常結果的統計時去掉前10個脫落周期,將后50個周期內的統計數據作為有效數據進行模型的對比。計算結果進行時間與空間平均。圖3中給出了以標準網格計算結果為例的圓柱繞流升力系數(C l)、阻力系數(C d)的時程(U∞/D無量綱化)變化曲線。可以看出Re＝3900時的升力幅值已不再穩定,但仍呈現出周期性變化趨勢,同時阻力系數表現出強烈的脈動現象,并在一平均值附近上下擺動。

圖3 升力、阻力系數隨時間變化及升力頻譜Fig.3 Time history of lift C l,drag C d coef ficients

圖4中給出了由升力系數時程曲線經過傅里葉變換(FFT)獲得的渦脫落頻率功率譜,由此可以計算渦脫落頻率f及斯特勞哈數S t(S t＝f D/U∞)。各模型阻力系數(C d)及斯特勞哈數S t見表2。

圖4 升力頻譜Fig.4 Spectra of lift

圖5為四種模型基于標準網格計算得到的圓柱繞流流場二維瞬時(t＝300)渦量分布及用軸向速度染色的三維Q分布,對比可知:由于RANS模型湍流黏性較大,抹去了很多重要的流場細節,計算結果只捕捉到大尺度的脫落渦結構,Q圖也只先顯示出近似二維的流動結構,這說明RANS模型基本上沒有求解小尺度流動的能力；SAS模型及PANS模型均捕捉到豐富的流動結構,二維渦量及三維Q值均顯示出復雜的周期性渦脫落現象。分析三者的Q圖可清晰地發現附著于壁面的二維層流剪切層及分離區流向與展向相嵌套的三維無序渦體結構。SAS模型與PANS模型均允許形成湍流譜,表現出預期的類似LES模型的求解小尺度運動的能力。同時,仔細對比SAS模型與PANS模型的結果可以看出,PANS模型能捕捉到比SAS模型更豐富的湍流結構。

圖5 不同模型計算得到的流場瞬時渦量與Q值圖(t＝300)Fig.5 Instantaneous vorticity and Q of different models(t＝300)

由實驗及以往計算結果[23]可知,圓柱繞流壁面剪切層的發展對外界影響因素非常敏感,微小外部干擾很容易造成邊界層的提前分離,使得剪切層變短,進而影響回流區及整個流場的測量或計算結果。圖6為用渦量等值線表示的標準網格條件下四種模型的瞬時(t＝300)剪切層,通過對比可知剪切層長度關系為:SAS＞PANS(des)＞PANS(tanh)＞SST。

圖6 不同模型瞬時分離剪切層示意圖(t＝300)Fig.6 Instantaneous separating shear layers of different models(t＝300)

3.2 回流區速度分布

圖7為以SAS模型為例的y＝0平面軸向速度時均圖,可以清晰地看出在圓柱近尾跡區域形成一個流速與來流相反的區域,即圓柱繞流的回流區。圖8為圓柱下游尾跡區中心線上時均軸向速度分布。由圖可知,圓柱背風點處速度為0,速度為逐漸增大的負值,到達回流區中心時速度負值最大。背風點與空間流動的再附點即流向速度恢復到0的點之間的距離即為回流區長度(L r/D)。四種模型均模擬出了圓柱后的速度分區,但彼此間差別較大,特別是對回流區的模擬。圖8(b)圖是對回流區中心線時均軸向速度的放大圖。首先需要說明的是用空心圓圈表示的實驗數據是Lourenco&Shih(1993)用PIV測量獲得[20],用實心圓表示的實驗數據是Parnaudeau等(2008)同樣用PIV測量獲得[21],可以看到兩者實驗測得的回流區長度差別較大。最近幾年的文獻也出現了與Parnaudeau實驗接近或與Lourenco實驗接近的兩種數值計算結果,有意思的是Kravchenko等(2000)在用B-Spline伽遼金方法對Re＝3900進行的LES數值計算中[23],最先發現了數值結果與Lourenco實驗數據在回流區與近尾跡區速度型的差別。Kravchenko計算的回流區長度大于Lourenco實驗值,其當時推測可能有外加擾動導致Lourenco實驗中圓柱壁面剪切層過早分離,造成剪切層變短,進而影響回流區長度。Parnaudeau實驗數據在回流區及速度型方面均驗證了Kravchenko的數值計算結果。由于實驗時間較晚,實驗方法更先進、嚴謹,本文中我們認為Parnaudeau的實驗值是更可信的。分析圖8(b)可知,SST模型計算的圓柱回流區長度誤差較大,SAS與PANS計算的回流區長度關系為SAS＞PANS(des)＞PANS(tanh)。三種模型計算的回流區區域位于兩個實驗值之間,與Parnaudeau實驗值仍存在一定誤差,其中SAS模型與Parnaudeau實驗最接近。以上結論與圖6中得出的剪切層長度結論也是一致的。

圖7 y＝0平面軸向速度時均分布Fig.7 Mean streamwise velocity along the y＝0 surface

圖8 圓柱尾跡中心線上時均軸向速度分布Fig.8 Mean streamwise velocity along the wake center line

圖9～圖11為圓柱繞流下游不同截面處的時均軸向速度分布(圖例見圖8)。可以看到軸向速度流型從近尾跡區到遠尾跡區由U型向V型轉變,結合前部分析可知,剪切層過早分離同樣會導致速度型的過早轉變,圖中兩種實驗值的對比也說明了這一點。圖9近壁x/D＝0.58時,四種模型的速度型均為U型,彼此差別不大,而到回流區x/D＝1.06時,四種模型出現差別,SST模型為完全的V型,SAS模型與兩種PANS模型同樣沒有計算出更加正確的U型,而是介于U型與V型之間,其中SAS模型與Parnaudeau實驗得到的U型更接近,同時PANS(des)要稍好于PANS(tanh)；在近尾跡回流區后部x/D＝1.54、2.02位置處,除了SST沒有計算出正確的速度型,SAS模型與兩種PANS模型的計算結果只是速度峰值與實驗值存在一定誤差,整體均與實驗值吻合較好；在遠尾跡區x/D＝4、7、10位置處,四種模型計算的速度型均較好,速度峰值與實驗存在較小誤差。以上分析說明近尾跡區域特別是回流區流動較為復雜、敏感,計算控制更困難,同時遠尾跡區受近壁區影響較小,使得遠尾跡區計算誤差小于近尾跡區。

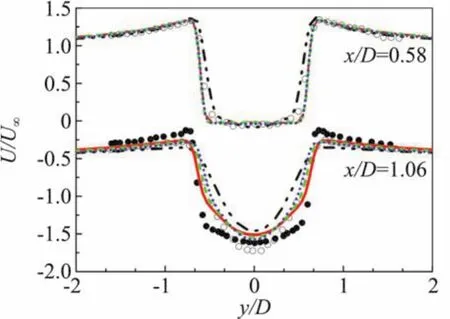
圖9 不同截面的平均軸向速度分布(x/D＝0.58,1.06)Fig.9 Mean streamwise velocity at different surfaces(x/D＝0.58,1.06)

圖10 不同截面的平均軸向速度分布(x/D＝1.54,2.02)Fig.10 Mean streamwise velocity at different surfaces(x/D＝1.54,2.02)

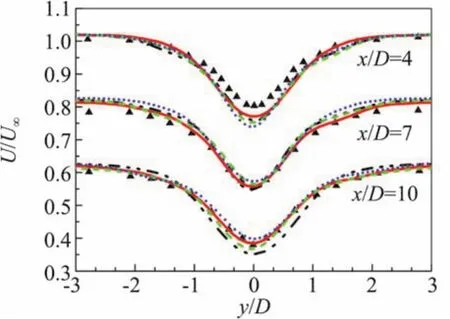
圖11 不同截面的平均軸向速度分布(x/D＝4,7,10)Fig.11 Mean streamwise velocity at different surfaces(x/D＝4,7,10)

圖12為圓柱繞流下游近尾跡回流區附近不同截面處的時均橫向速度分布(圖例見圖8)。由x/D＝1.06處的時均橫向速度與實驗值可以看到,SAS與兩種PANS模型得到的速度型均與Parnaudeau實驗值較吻合,與SST模型比較顯示出較高的計算精度。x/D＝1.54、2.02處的對比結果可以看出四種模型在速度型與峰值上均存在一定誤差,與軸向速度計算結果類似。

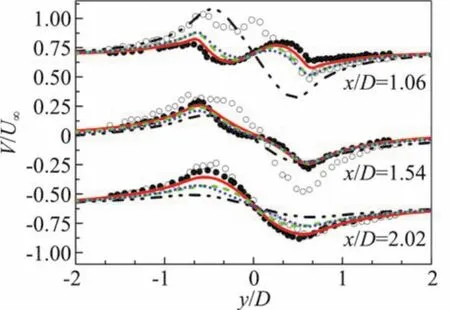
圖12 不同截面的平均橫向速度分布(x/D＝1.06,1.54,2.02)Fig.12 Mean cross-flow velocity at different surface(x/D＝1.06,1.54,2.02)

3.3 加密網格計算結果

根據混合模型的構造原理可知,其湍流尺度求解能力是基于對渦黏性的控制作用。圖13為三種混合模型計算的圓柱繞流時均湍動黏度μt/μ(湍動黏度與來流黏度之比)分布,上部為標準網格計算結果,下部為加密網格計算結果。僅從數值來看,SAS模型與兩種PANS模型的湍動黏度分布關系為SAS＞PANS(des)＞PANS(tanh)。PANS模型所求湍動黏度要小于SAS模型,這也解釋了圖4中PANS模型對流場的捕捉要好于SAS模型。但需要注意的是,較低的湍動黏度不一定獲得較準確的數值計算結果。由文中氣動力的比較可知,SAS模型要好于PANS模型。通過比較網格加密后的湍流黏度可知,兩種PANS模型在近壁網格密集區域出現了湍流黏度較低的區域,這是由于PANS模型的f k構造函數仍是由當地湍流尺度和網格尺度來控制,在近壁網格較密的條件下,PANS模型顯現出類似DES模型對網格敏感的缺點,這時近壁RANS區域被破壞,而網格尺度還沒有小到能夠進行大渦模擬的程度。

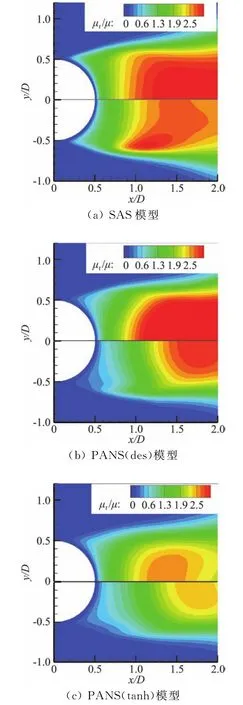
圖13 時均湍流黏度比(μt/μ)分布(標準網格：上,加密網格：下)Fig.13 Time-averaged distributions ofμt/μ(baseline grid：top,fine grid：bottom)

圖14為三種混合模型在不同網格條件下計算的局部(x/D＝1.06)時均軸向雷諾應力分布(圖例見圖15)。可以看到SAS模型及兩種PANS模型計算的雷諾應力與實驗值均有較大差距,這可能是由于渦黏性模型的內在缺陷造成的。我們在此關注不同的模型在不同網格條件下的計算差異。可以看到SAS模型在標準網格與加密網格條件下均高估了雷諾應力值,但兩種網格下的計算結果差別不大；兩種PANS模型對不同的網格表現出相似的規律,在加密網格時雷諾應力均出現了明顯的降低,結合圖13中的黏度分布可知,由于近壁區域網格的加密,湍流黏度降低,導致模化的雷諾應力減少,同時有沒有求解足夠的雷諾應力,導致了雷諾應力不足現象的發生,這也驗證了PANS構造函數對網格較敏感的缺陷。同時兩種PANS模型函數比較可以看出,PANS(des)模型計算的雷諾應力及氣動力分布要稍優于PANS(tanh)模型,這也說明了PANS(tanh)模型構造函數對網格的敏感程度要大于PANS(des)模型的構造函數。

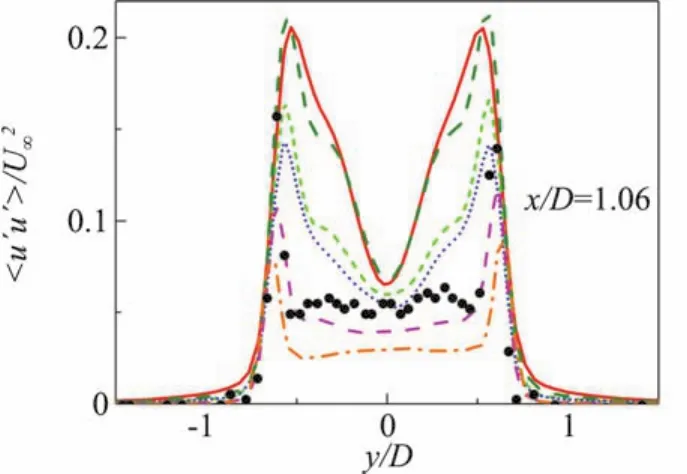
圖14 局部時均軸向雷諾應力分布Fig.14 Time-averaged distributions of streamwise Reynolds stress

圖15為三種模型在不同網格條件下的時均軸向速度分布對比。結合前文分析可知,SAS模型網格獨立性較好,標準網格與加密網格下的計算結果沒有體現出太大差別,且由于對剪切層的計算更準確,計算得到的回流區大小更接近實驗值。兩種PANS模型由于對網格較敏感,在加密網格時延緩了剪切層的轉捩,導致回流區變長。這在PANS(tanh)模型的計算結果中表現更明顯。

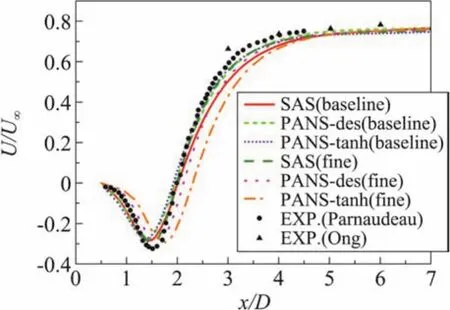
圖15 時均軸向速度分布Fig.15 Time-averaged distributions of streamwise velocity

3.4 積分統計量比較

表2為四種模型計算的圓柱繞流平均積分統計量與相關實驗值及數值結果對比。可以看到在與剪切層運動密切相關的參數中,普通網格下SAS與兩種PANS模型均取得了與實驗值較吻合的回流區長度(L r/D)計算結果,與構造相對完善的LES-THE、SA-IDDES、V2-f-DES模型的計算結果也是相近的,其中SAS模型的計算結果與實驗值最接近；加密網格時,兩種PANS模型均過大地預測了回流區長度。在阻力系數(C d)及分離角(θSep)的計算中,在標準網格下三種混合模型計算誤差均較小,C d滿足實驗值的0.98±0.05區間,在加密網格時,SAS模型的計算結果變化不大,兩種PANS模型獲得了較小的分離角及阻力系數。在其余的比較項中,可以看到四種模型對圓柱尾跡旋渦脫落頻率的計算及壁面壓力的計算均較準確,所計算的斯特勞哈數(S t)與背風點壓力系數(-C pb)差別不大。對于SST模型,由于其構造模化了所有的湍流量,導致重要的流場細節被抹平,其計算的阻力系數、背風點壓力系數、回流區長度、分離角均存在較大誤差。同時可以看到兩種網格條件下PANS(des)計算結果稍好于PANS(tanh)。比較文獻[25]中兩種f k為常數的PANS模型計算結果可以看出,f k＝0.1時,流場f k值已處于較低水平,但計算的回流區長度要小于本文變f k計算結果,而f k＝0.3時的計算結果誤差已較大,這說明了變f k在流場計算中更合理,同時也說明了流場對f k值是比較敏感的。

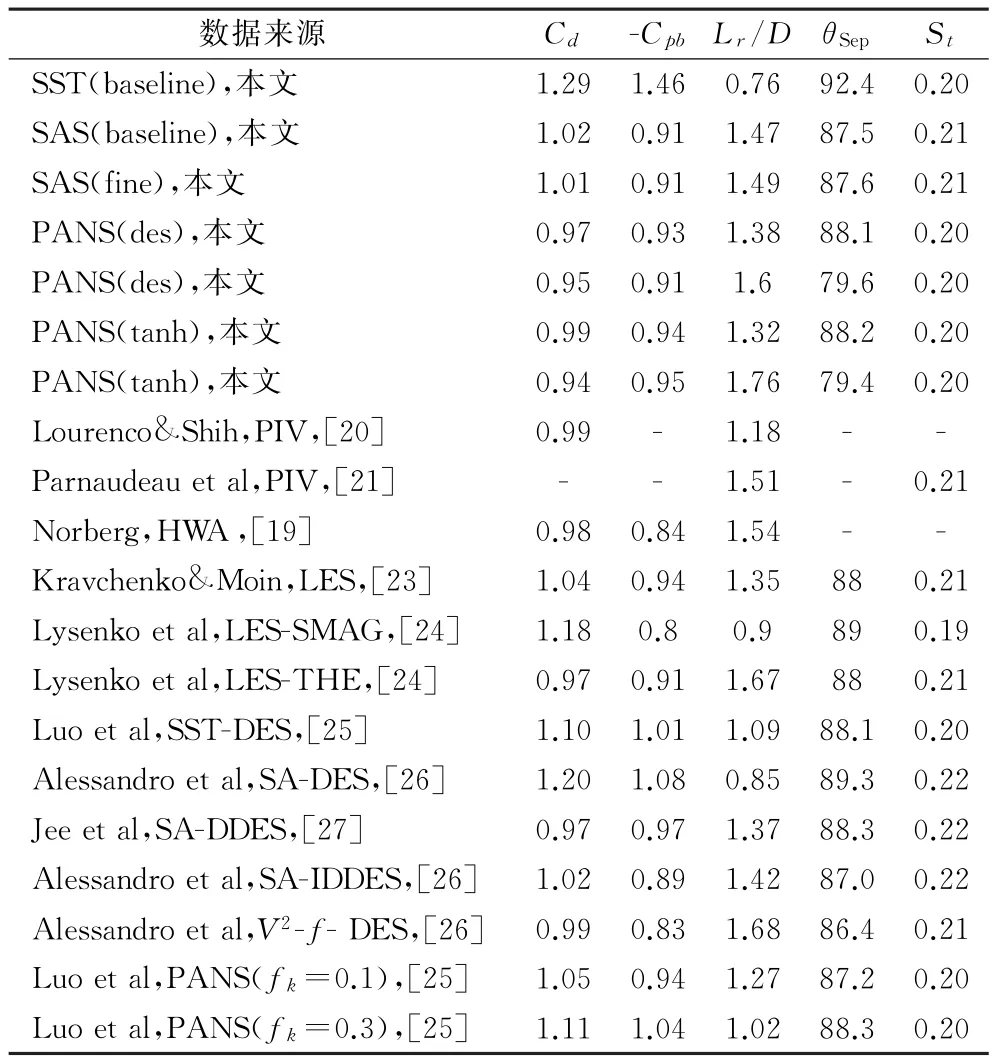
表2 圓柱繞流平均積分量對比Table 2 Summary of the mean integrated quantities for the cylinder flow

3.5 混合模型調控機制比較

由前述分析可知,SAS及PANS等渦黏性混合模型均能通過降低流場湍動黏度來求解更多湍流尺度,但SAS及PANS對求解尺度的調控機制是完全不同的。由前文模型構造我們可知,SAS模型中引入了von Karman長度尺度L vk,通過當地湍流尺度L與L vk的比例關系來控制ω輸運方程中源項QSAS的生成量,因此SAS模型在分離區是通過L/L vk的調控作用來增大ω的值,從而降低湍動黏度的值；PANS模型是通過加入一個f k參數來調控流場可解/不可解湍流量的比例,f k值越小,可解尺度就釋放的越多,文中PANS模型使用了兩種變f k函數,其核心是當地湍流尺度與網格尺度的比例關系,兩者都是通過減小ω方程中耗散項的量,從而使求解的ω值增大,進而使湍動黏度減小。

圖16為SAS模型計算的瞬時及時均L/L vk分布。可以看到在尾跡分離區L/L vk的值較大,而在遠場區L/L vk基本為0。圖17和圖18是兩種變f k的PANS模型計算得到的瞬時及時均f k分布,可以看到在分離區f k的值處在較低水平,而在遠場范圍f k＝1湍流信息均被模化。通過比較兩類模型中對渦黏度起關鍵調控作用的L/L vk與f k分布可以看出,立足于當地流動、對網格無依賴的SAS模型局部分辨率更高,可以反映出流場結構的無序與豐富狀態。PANS模型中網格尺度的關聯性使得其局部分辨率降低,且計算結果對網格及計算初值設置非常敏感。從以上來看,SAS模型對流場渦黏性的調控機制是有優勢的。

圖16 SAS模型計算的瞬時及時均L/L vk分布Fig.16 Time-averaged and instantaneous distributions of L/L vk for SAS

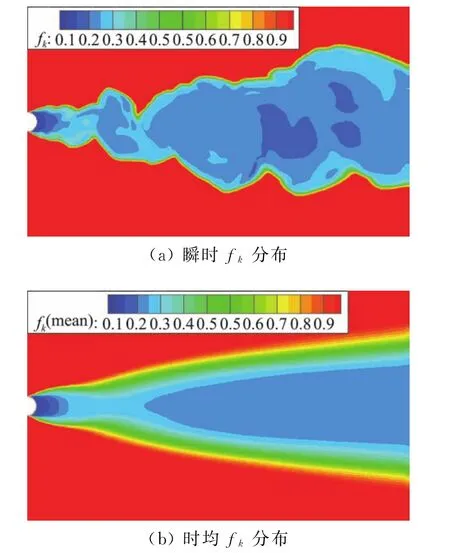
圖17 PANS(des)模型計算得到的瞬時及時均f k分布Fig.17 Time-averaged and instantaneous distributions of f k for PANS(des)

圖18 PANS(tanh)模型計算得到的瞬時及時均f k分布Fig.18 Time-averaged and instantaneous distributions of f k for PANS(tanh)

對比圖17和圖18,顯示了PANS模型的兩種函數計算的f k分布差別不大,在近尾跡區f k均處在較低水平,這有效地調整了流場的求解尺度。同時可以看到PANS(des)模型相比PANS(tanh)模型在近尾跡區的分辨率更高,其在回流區后部及遠尾跡區的f k值要稍小于后者。分析兩種模型的構造可知,PANS(des)模型f k函數構造相對簡單,但其對流場的調控作用更加直接和靈敏,而PANS(tanh)模型中f k函數中借助tanh函數,tanh函數整體從－1～1變化,這使得函數的整體靈敏度下降,從而影響f k的分布。同時圖13中可以看到PANS(des)的湍動黏度稍高于PANS(tanh),其獲得的氣動力分布也稍好于后者。這也說明了兩種變f k函數比較,類DES的f k調控函數更好一些,計算的湍流耗散也更合理。

4 結 論

本文以Re＝3900的圓柱繞流作為算例比較了SAS、PANS(des)、PANS(tanh)湍流模型在大分離流動中的計算能力,主要從流場特征捕捉、氣動力特性計算、流場渦黏性控制等方面對所用湍流模型進行了比較,并通過不同的網格計算條件對比了不同模型調控函數的網格敏感性。計算結果表明:三種混合模型均具有求解三維小尺度渦運動的能力,并能較完整地展現出亞臨界雷諾數下圓柱繞流層流剪切層形成、發展、失穩、分離,在下游近尾跡區形成回流區直至遠尾跡區形成剪切分離區的過程。同時,通過對比計算結果得到以下結論:

1)在對湍流結構的顯示方面,PANS模型相比SAS模型能捕捉到更豐富的湍流結構,兩類模型對流場氣動力的計算均存在一定誤差,回流區計算誤差要大于遠尾跡區,三種模型氣動力計算與實驗吻合關系為SAS＞PANS(des)＞PANS(tanh)。

2)SAS模型L vk尺度立足當地流動,局部流場分辨度更高,調控作用更強；PANS模型對網格設置較敏感。兩類模型相比,SAS模型的流場信息調控模式更優秀,獲得的流動渦黏性更合理。

3)兩種PANS模型中,類DES可變f k分布函數構造相對簡單,所得f k分布更準確；借助tanh函數的f k分布函數調節靈敏度較低,計算得到的尾跡區f k值偏低,對流場調控作用稍差。