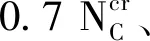軸向受載鐵木辛柯梁的彎曲研究

王續宏， 李翔宇

(西南交通大學 力學與工程學院， 四川 成都 610031)

0 引 言

軸向受載的梁由于其能夠提升抗拉和抗彎強度而被廣泛應用于工程建設中.例如，在宏觀尺度上，軸向受載梁經常被用在橋梁、鐵路和隧道等基礎設施建設和航空工業中的關鍵部位[1-2]；而在微納米尺度，軸向受到壓力的納米線常被埋在PDMS基體中構成結構的一部分[3-5].因此，軸向受載的梁的變形行為是一個很重要的研究課題.例如，Simsek等[6-7]基于鐵木辛柯梁理論，采用修正的偶應力理論和高階梁理論研究了功能梯度納米梁的彎曲問題；Ansari等[8]為了修正鐵木辛柯梁理論，采用應力梯度彈性理論考察了橫向剪切變形的影響；Li等[9]采用拉格朗日運動關系研究了考慮摩擦影響的棱柱鐵木辛柯梁的大變形問題；Tuna等[10]基于初始積分模型，研究了歐拉—伯努利梁和鐵木辛柯梁的靜力彎曲行為并得到了解析解.

事實上，對于鐵木辛柯梁軸向力在變形時的方向有兩種不同的假設：一種認為，軸力的方向沿著中性軸的方向[11-13]，另一種認為，軸力的方向垂直于變形后的橫截面[14-15].對此，Chen等[16]通過引入躍遷系數建立了一個統一的鐵木辛柯梁模型，并研究了梁的強迫振動.但隨著躍遷系數的引入，有許多典型的問題需要解決，比如新近提出的梁模型的靜態響應問題.對此，本研究主要分析了躍遷系數對軸向受載鐵木辛柯梁彎曲行為的影響：首先，推導出了控制方程，再通過拉普拉斯變換對其進行處理，得到了方程的解析解；其次，展開數值計算驗證當前解的正確性并考察了躍遷系數對鐵木辛柯梁彎曲行為的影響.

1 問題描述和解決

1.1 問題描述

在笛卡爾坐標系Oxy中，考慮一個長為L、高為h，在軸向和橫向分別受力為T和P的梁(見圖2).梁的材料參數為：楊氏模量為E，剪切模量為G，密度為ρ，橫截面面積為A，慣性矩為I.

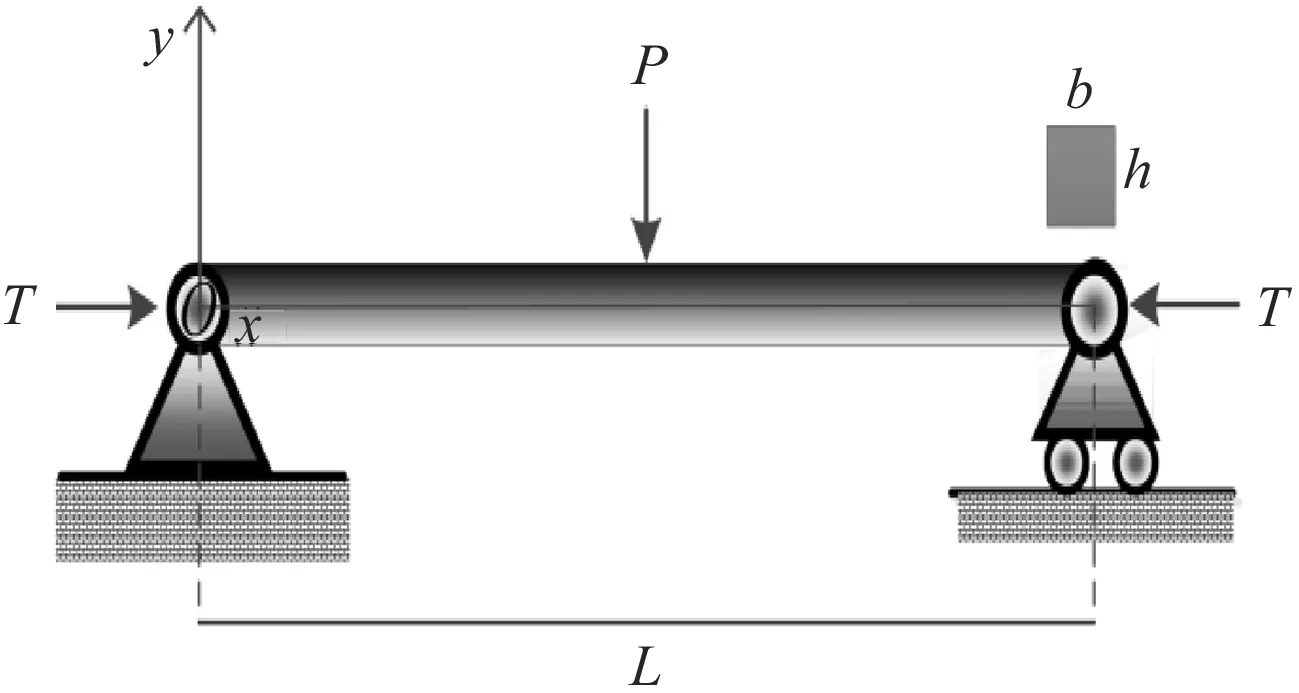
圖1鐵木辛柯梁模型示意圖

由文獻[16]可得軸向受載鐵木辛柯梁的控制方程為，

EIφ″+(κGA+αT)(w′-φ)=0

(κGA+αT)(w″-φ′)-Tw″=P

(1)

式中，w和φ分別表示撓度和轉角，α表示軸力方向的躍遷系數.在本研究中，α在0到1之間變化，當α=0時，對應軸力的方向沿著中性軸的方向，當α=1時，對應軸力的方向垂直于變形后的橫截面，壓力(或拉力)被假定為正(或負).將(1)式表述為撓度的方程，可以得到，

w″″+a2w″=f(x)

(2)

其中，

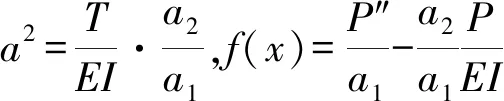
(3)

a1=κGA-(1-α)T,a2=κGA+αT

(4)

式中，κ為剪切修正系數.

假定在梁上任意點x0處受到一個大小為P的集中力，則方程為，

(5)

式中，δ()為狄拉克函數.式(5)的解是數學上的格林函數解，對于解決很多相關的問題十分重要.例如，在梁上施加一個分布力P(x)，可通過疊加原理得到相應的撓度，

(6)

1.2 拉普拉斯變換

根據已經給出的控制方程，對式(5)關于坐標x進行拉普拉斯變換，可以得到，

(7)

式中，w(0)、w′(0)、w″(0)、w?(0)是待定常數，s是拉普拉斯復數.對式(7)進行拉普拉斯逆變換可以得到，

w(x;x0)=H(x-x0)Ψ1(x-x0)+w(0)Ψ2(x)+

w′(0)Ψ3(x)+w″(0)Ψ4(x)+w?(0)Ψ5(x)

(8)

式中，H(x)是單位階躍函數.

方程Ψi(x)的定義如下，

(9)

通過拉普拉斯變換可得到式(5)的通解，而式(8)中的待定常數可以通過邊界條件進行確定.

1.3 待定常數的確定

通過邊界條件可確定相應條件下顯式表達式所需的待定常數.在確定這些常數之前，先得到轉角φ、彎矩M和剪力V確切的表達式如下所示，

(10)

由式(8)可得，

(11)

本研究中考慮4種常見的邊界條件，即簡支梁、固支梁、懸臂梁、一端簡支一段固支的梁.其中，對于簡支梁，w(0)=0,M(0)=0,w(L)=0,m(L)=0；對于固支—簡支，w(0)=0,φ(0)=0,w(L)=0,M(L)=0;對于固支梁，w(0)=0,φ(0)=0,w(L)=0,φ(L)=0；對于懸臂梁，w(0)=0,φ(0)=0,M(L)=0,V(L)=0.

如此，可以通過邊界條件確定相應的待定常數，將其代回(8)式中，便可以得到多種邊界條件下撓度的顯式表達式.

2 數值分析

考慮兩種類型的力，即集中力和分布力，將其施加在一個特定參數的鐵木辛柯梁上.材料具體參數如下，E=7.0×1010N/m2,G=2.61×1010N/m2，L=0.5 m,κ=0.87,ρ=2 778 kg/m3，橫截面是高為h的正方形.為了方便計算，引入以下的無量綱參數，

式中，nH和nC為無量綱化的軸向壓力，η表示高跨比.簡支梁和固支梁的臨界屈曲力分別是，

(12)

2.1 解的有效性

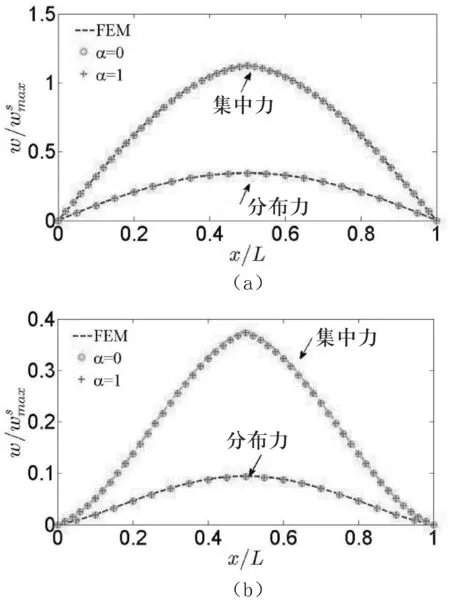
為了驗證當前結果的有效性，本研究對解析解和有限元(FEM)結果進行對比，考慮以下兩種情形：其一，在梁的中點處施加單位大小的集中力；其二，在梁表面施加集度為單位力的分布力.這兩種情形下，梁的高跨比均為0.2，且都在軸向受到一個單位大小的力.在數值模擬計算中，采用商業有限元軟件ANSYS 15.0，并用BEAM 188梁單元劃分網格.在模擬中，設有1 000個單元和2 002個節點.

由圖2可以看出，解析結果和有限元結果較為吻合，這在一定程度上證明了結果的有效性.

2.2 躍遷系數對撓度的影響

在梁的中點處施加一個單位大小的集中力，并在軸向施加不同等級的軸力，來觀察梁撓度的變化.

為了量化躍遷系數α對靜撓度的影響，定義相對誤差為，

圖3簡支梁和固支梁相對誤差隨高跨比和軸向壓力的變化

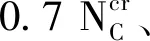
3 結 論