基于SNP系統的改進粒子群聚類算法
李 立
(安慶廣播電視大學, 安徽 安慶 246003)
0 引 言
在眾多的聚類分析算法中,K-means是基于劃分的經典聚類算法,具有局部尋優能力強、聚類速度快和易于實現的優點,但該算法也存在聚類結果過于依賴初始聚類中心點、波動性大且易于陷入局部極值的缺點.對此,有學者提出了基于多種粒子群優化(Particle swarm optimization,PSO)的聚類算法[1-2],即將PSO算法的全局尋優能力和K-means算法的局部尋優能力相結合來改善聚類算法的性能,并取得了一定的效果.但是,PSO算法在實現優化時會出現早熟收斂現象,且具有較強的隨機性,在實際應用中具有一定的局限性.針對該問題,有學者提出一種以生物細胞為原型的膜計算算法模型[3],其可將細胞區域劃分成各自獨立的計算單元,具有強大的計算能力.目前,脈沖神經膜(Spiking neural P,SNP)系統是基于神經型的膜計算模型,也是膜計算領域的研究熱點之一[4-7].本研究在粒子群聚類算法中引入SNP系統,構建了一種基于SNP系統的改進PSO-KM模型,即SNPS-PK算法,其原理是將初始聚類中心的各種組合作為粒子,將其分配到若干個神經元,并在神經元中進行粒子群的迭代與進化,利用SNP系統的高并行性和PSO算法的全局尋優能力在更短的時間內得到更優化的初始聚類中心,為下一步K-means算法的局部尋優提供更好的聚類初值,以進一步提升聚類結果的穩定性和準確率.
1 概念及定義
1.1 PSO算法
PSO算法是一種仿生方法,粒子之間通過相互協作并不斷迭代來生成最優解,其實現步驟如下:
假設含M個粒子的群體在一個N維空間進行搜索,粒子i(1≤i≤M)的位置、速度和歷史最優位置分別用3個維向量來表示,Xi=(xi1,xi2,…,xiN),Vi=(vi1,vi2,…,viN)和Pbesti=(Pbesti1,Pbesti2,…,PbestiN).整個粒子群的全局最優位置可表示為,Gbest=(Gbesti1,Gbesti2,…,GbestiN).在迭代過程中,粒子更新速度和位置如式(1)與式(2)所示.
Vi(t+1)=ωVi(t)+c1r1(Pbesti-Xi)+
c2r2(Gbest-Xi)
(1)
Xi(t+1)=Xi(t)+Vi(t+1)
(2)
其中,ω為慣性權重,c1和c2為學習因子,r1和r2為隨機權重.
1.2 K-means算法
K-means算法是一種基于質心的啟發式聚類算法,其實現步驟如下:
1)在n個數據樣本中隨機選擇k個Ci(i=1,2,…,k)作為初始聚類中心;
2)計算其他數據樣本與初始聚類中心的距離,若數據樣本Xj屬于第i聚類,則其權重值wji=1,否則為0,如式(3)所示:
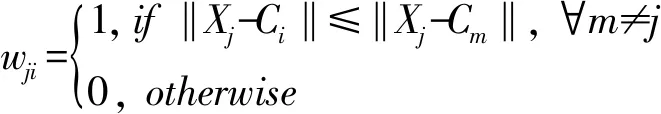
(3)
3)由式(4)計算目標函數J,若J值不變,則停止迭代,算法結束.否則,進入步驟4),
(4)
4)由式(5)更新聚類的中心點,回到步驟2).
(5)
1.3 SNP系統的定義
一個標準SNP系統的定義為,
Π=(O,σ1,σ2,…,σm,syn,in,out)
(6)
其中:
1)O={a}是脈沖a的集合.
2)σ1,σ2,…,σm是系統Π中所含的m(m≥1)個神經元,σi=(ni,Ri)(1≤i≤m),其中,ni表示σi中脈沖的初始值,而Ri表示兩類規則的集合:
(1)激發規則.E/ac→a;d(c≥1,d≥0),E為a的正則表達式,d為時延.若神經元σi在某時刻有k個脈沖,且ak∈L(E)(k≥c),則利用規則E/ac→a激發,消耗c個脈沖,并在d步之后向相關神經元分別發送1個脈沖.
(2)遺忘規則.as→λ(s≥1),對Ri中的任意規則E/ac→a;d,都滿足as?L(E).若神經元σi在某時刻有且僅有s個脈沖,則利用規則as→λ,消耗掉所有的脈沖,且不會產生新的脈沖.
3)syn?{1,2,…,m}×{1,2,…,m}表示神經元之間的突觸.其中,(i,j)∈syn,(1≤i,j≤m,i≠j).
4)σin和σout分別表示輸入和輸出神經元,其中,in,out∈[1,2,…,m].
2 基于SNP系統的改進粒子群聚類算法
本研究將SNP系統與PSO算法、K-means算法相結合,構建了一種基于SNP系統的改進PSO-KM模型的SNPS-PK算法,以進一步提升聚類結果的穩定性和準確率.
2.1 粒子群的適應度函數和編碼方案
聚類分析時,PSO算法的適應度函數用來評價k個聚類中心的性能,其定義為,
(7)
其中,f(x)是粒子在位置x處的適應度值Zj(1≤j≤k),是類Cj的聚類中心,Xi是集群中的數據樣本.粒子的f(x)可以衡量數據對象的結合程度,f(x)越小表示結合越緊密,聚類效果越好.
PSO算法的優化目標就是搜索到f(x)值最小的粒子位置,其對應的就是優化后的初始聚類中心.粒子i在第(t+1)次迭代時,如果f(xi(t+1)) 采用PSO算法對K-means算法的初始聚類中心優化前,k個聚類中心Zj(1≤j≤k)映射成集群中的粒子,其坐標向量組成了粒子在優化過程中的位置,而粒子i的適應度值為f(xi)(1≤i≤k).每個粒子代表某種可行解,粒子的編碼由k個d維聚類中心中粒子的位置、速度和適應度值組成,其編碼方案為, Z11…Z1dZ21…Z2dZk1…Zkd‖V11…V1dV21…V2dVk1…Vkd‖f(xi) 為了達到全局搜索和局部搜索之間的平衡,文獻[1]給出了一種慣性權重ω隨迭代次數的增加而線性下降的方法,其慣性權重ω的計算式為, ω(t)=ωmax-(ωmax-ωmin)t/ωmax (8) 其中,ωmax和ωmin分別是最大和最小慣性權重,t和tmax分別是當前迭代次數和最大迭代次數.ω的理想取值范圍為0.4~0.9. 在實際計算中,為了避免“振蕩”并讓粒子加快收斂到最優解,可在式(2)中增加飛行時間因子,則式(2)變為, Xi(t+1)=Xi(t)+H0(1-t/tmax)Vi(t+1) (9) 其中,t和tmax分別是當前迭代次數和最大迭代次數.H0為1.5. 式(1)中,學習因子c1和c2分別調節向Pbest和Gbest方向飛行的最大步長,c1是粒子自身學習的權重系數,c2是粒子群體學習的權重系數.為了平衡隨機因素的作用,一般情況下,c1=c2.而r1和r2被設置成介于[0,1]之間的隨機數,目的在于增加粒子飛行的隨機性. SNPS-PK算法的膜結構如圖1所示.神經元內的對象不是脈沖,而是粒子對應的位置,即不斷迭代的聚類中心. 圖1中的神經元1、2和3為輔助神經元,神經元4為主神經元,神經元5為輸出神經元.系統Π中輔助神經元粒子的主要功能是搜索可能存在最優解的領域并及時將搜索信息傳回主神經元.輔助神經元1和3中的粒子按照式(1)和式(2)更新速度和位置,按照式(8)進行慣性權重ω的調整.神經元內部每次迭代后,都根據適應度值對粒子進行優劣排序,將其中最優的s個粒子送入主神經元4. 圖1 SNPS-PK算法對應的膜結構 神經元1和3中的規則如下: 輔助神經元2中的規則如下: 主神經元4對從輔助神經元1、2和3接收到的3s個粒子進行重新迭代和排序,搜索到最優解. 主神經元4中的規則如下: SNPS-PK算法包括2個階段:在前階段,利用SNP系統的并行性和PSO算法的全局尋優能力進行全局搜索,在可行解空間內找到k個優化的初始聚類中心;在后階段,執行K-means算法,進行局部優化,并輸出最終的聚類結果. 其中,SNPS-PK算法前后兩個階段的轉換時機是根據適應度方差σ2來判定粒子群的收斂程度.適應度方差σ2定義如下, (10) 其中,m是粒子群的規模,favg是粒子適應度的平均值.當σ2很小時,粒子群的狀態已趨于收斂,此時即為SNPS-PK算法的轉換時機. 為了驗證SNPS-PK算法的有效性,本研究對其進行了仿真實驗測試. 實驗環境為:操作系統Windows 10,CPU 2.7 GHz InterCore(TM),內存4 GiB,編譯軟件為Edit with IDLE,用Python語言編程實現.本研究在3個數據集上測試SNPS-PK算法,其中包含1個真實數據集Iris及2個人工數據集Data1和Data2.在實驗中,分別在此3個數據集上運行SNPS-PK算法,得到的聚類結果如圖2~圖4所示. 圖2在數據集Iris上執行SNPS-PK算法 圖3在數據集Data1上執行SNPS-PK算法 圖4在數據集Data2上執行SNPS-PK算法 同時,實驗中還將SNPS-PK算法與標準K-means算法、PSO-KM算法進行了比較.三種算法的聚類準確率及運行時間的比較結果如表1所示. 由表1可知,三種算法中,K-means算法的準確率最低,SNPS-PK算法的準確率最高,PSO-KM算法介于兩者之間.PSO-KM算法利用PSO的全局搜索能力,此在一定程度上提升了聚類準確率.而SNPS-PK算法在PSO-KM算法的基礎上引入SNP系統,利用SNP系統的并行性進一步優化了聚類中心,并對慣性權重w和飛行時間因子H0進行動態調整,使SNPS-PK算法能夠更好地接近最優解,聚類準確率得以進一步提升. 表1 3種算法的聚類準確率及運行時間比較 本研究在粒子群聚類算法中引入SNP系統,將SNP系統的并行性和PSO的全局尋優能力相結合,使得初始聚類中心得以進一步優化,為下一步K-means算法的局部尋優提供了更好的聚類初值,提升了聚類結果的準確率.由于聚類算法與SNP系統的結合是一種新的研究思路,目前對其的研究仍主要集中在理論的探討上[8-9].因此,如何利用基于SNP系統的聚類算法解決實際問題是下一步的主要研究方向.2.2 SNPS-PK算法中的參數設置
2.3 SNPS-PK算法的膜結構
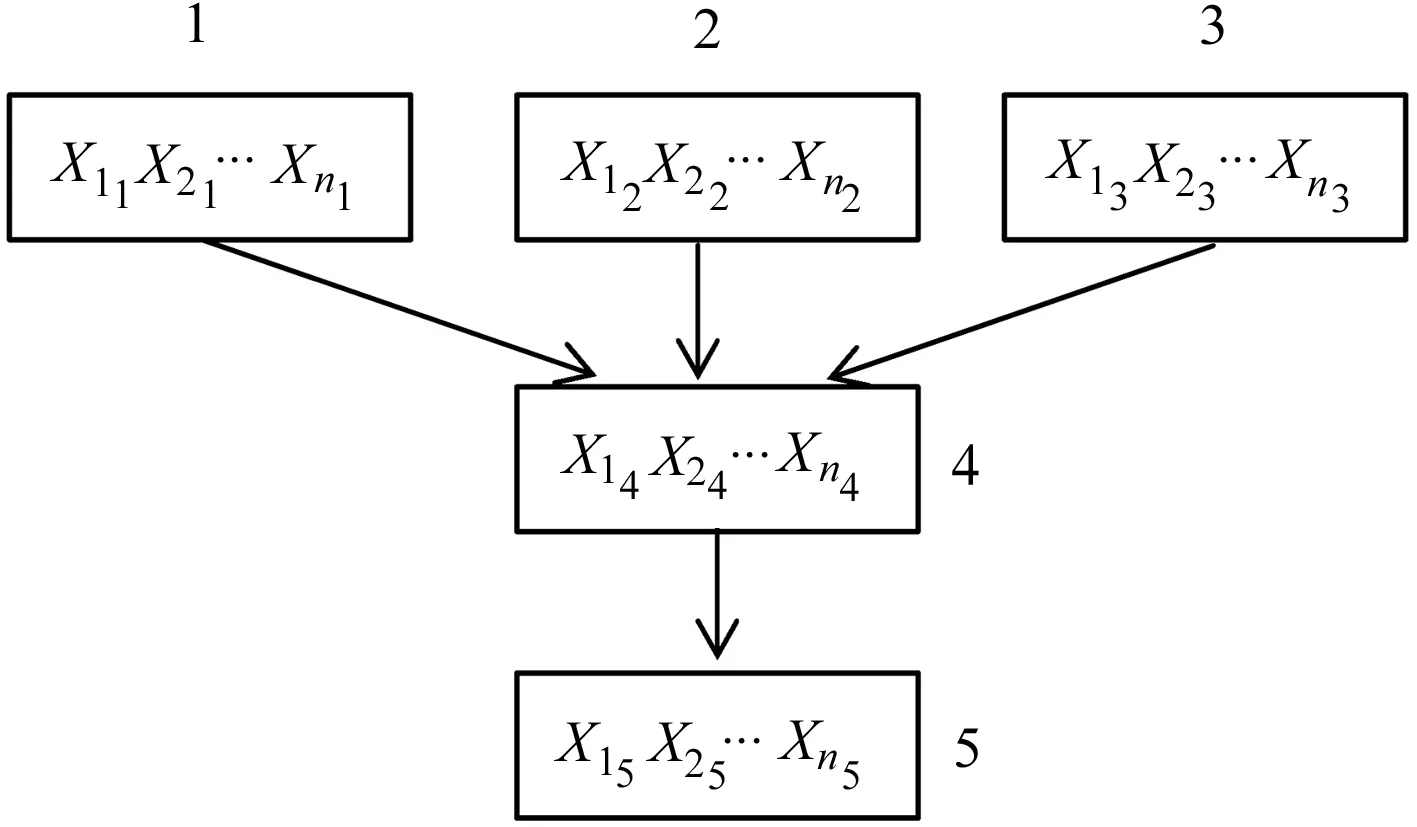
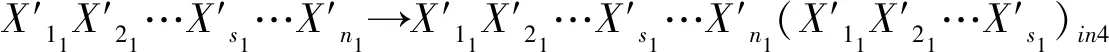
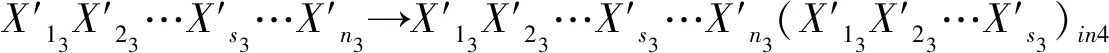
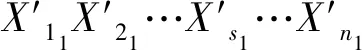

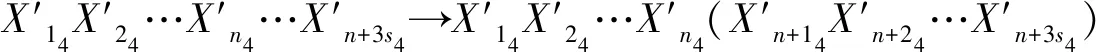
2.4 SNPS-PK算法的轉換時機
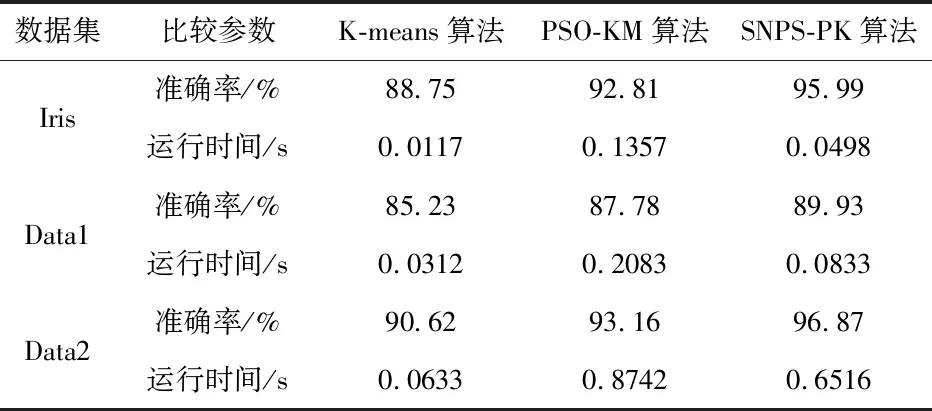
3 實驗與分析
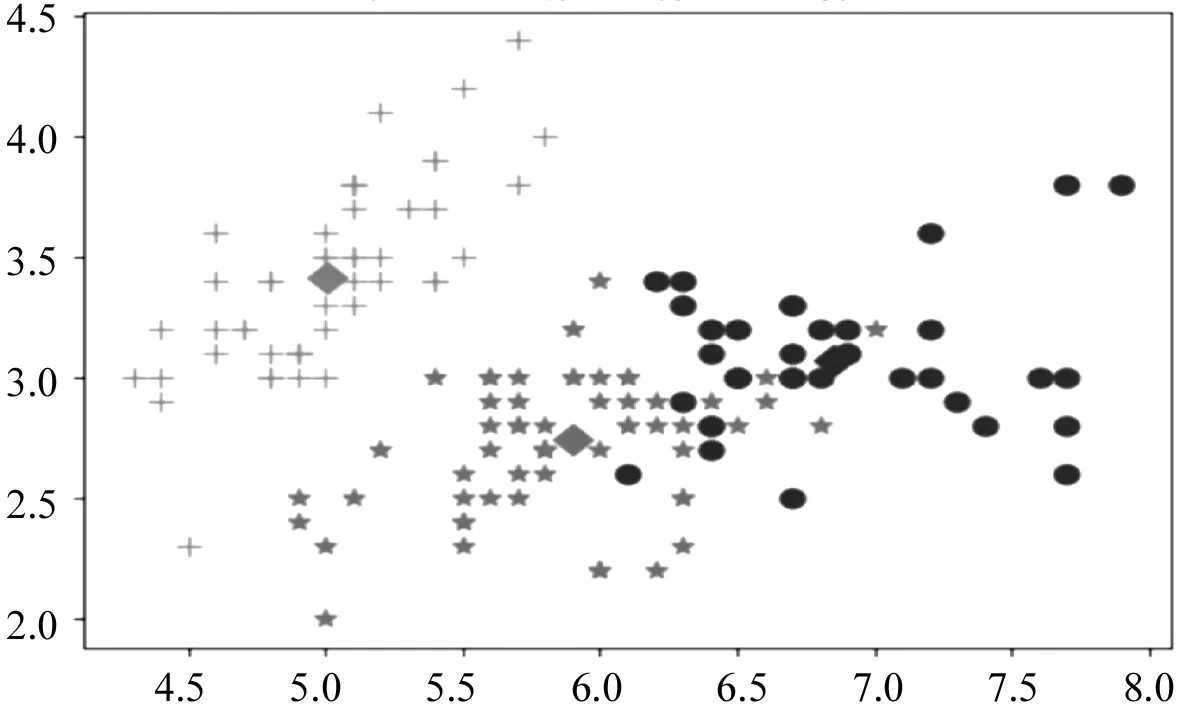
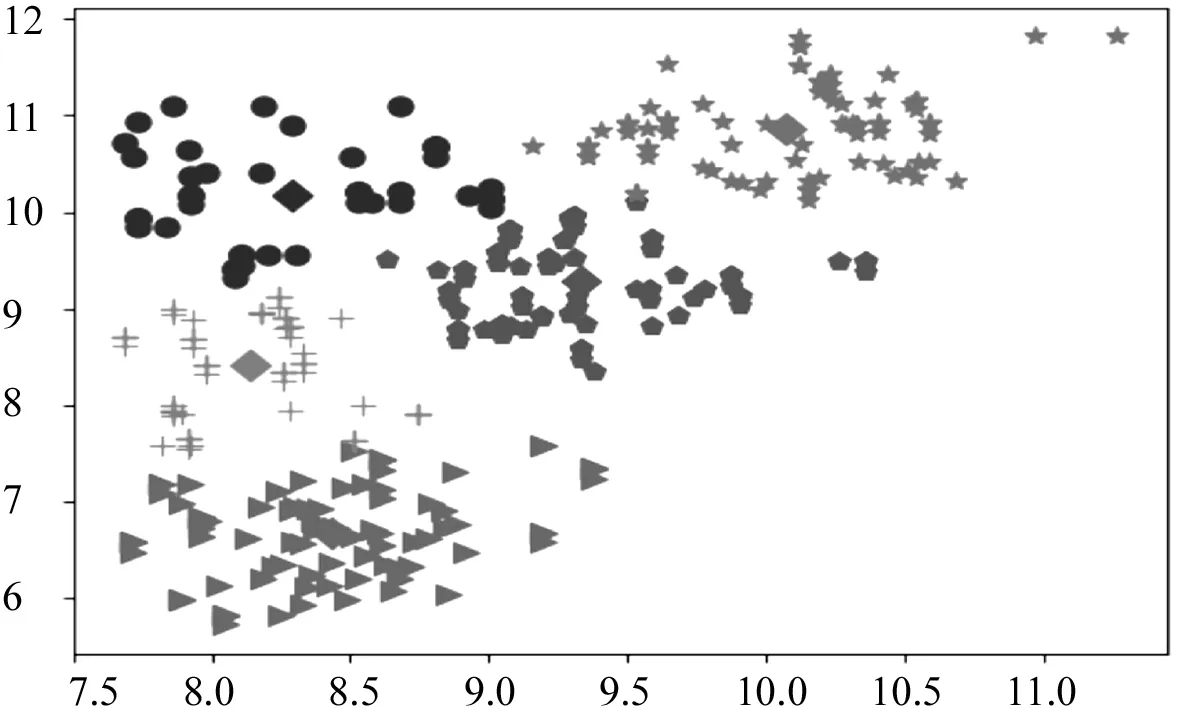

4 結 語

